基于爆炸成型弹丸(EFP)的大锥角喇叭罩成型规律

王雅君，李伟兵，李文彬，王晓鸣，王桂林

(1. 南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094；2. 重庆红宇精密工业有限责任公司，重庆 402760)

引 言

爆炸成型弹丸(EFP)是根据装药的爆轰作用，使药型罩被爆炸载荷压垮、闭合所形成的具有较高质心速度和一定结构形状的聚能侵彻体[1]。其中，药型罩作为聚能战斗部的关键部件，其结构是影响EFP 成型的主要因素。近年来，国内外学者针对新型药型罩结构开展了大量的研究，Fedorov S V[2]对半球-圆柱型组合药型罩进行了研究，提出该结构下聚能侵彻体飞行速度更高；Yi Y S[3]设计了一种可以形成尖头形EFP的锥弧结合型药型罩结构，试验中该结构下的EFP在远距离飞行时未断裂;徐文龙等[4]提出了给锥形罩头部附加一种圆台形装置来提高杆式射流头部速度的方法;王凤英等[5]基于二次喷射的原理提出了一种M形顶部药型罩聚能装药结构。对于组合药型罩，王庆华等[6]设计了一种圆柱-半球型药型罩结构，以提高射流头部速度；周方毅等[7]提出了一种圆锥-球缺型组合药型罩，可实现串联效果，圆锥部分形成金属射流进行开孔，随后球缺部分形成EFP对目标进行二次破坏。

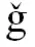
本研究基于大锥角喇叭罩的结构特点，利用LS-DYNA模拟计算软件分析其侵彻体成型过程，并以大锥角喇叭罩结构参数对侵彻体性能的影响为出发点，研究药型罩的虚拟罩高、喇叭曲率半径、圆弧曲率半径及罩厚等结构参数对侵彻体成型参数的影响规律，找出适宜于EFP毁伤元成型的大锥角喇叭罩结构参数组合。

1 药型罩结构设计及计算模型

1.1 药型罩结构设计

要形成良好的爆炸成型弹丸，药型罩结构形状与尺寸具有重要作用。本研究以较为成熟的弧锥结合罩为基准，装药口径取100mm，并保持药型罩罩顶高与罩厚不变，得到弧锥结合罩、大锥角喇叭罩、球缺罩3种药型罩结构方案。其中弧锥结合罩基于相关文献[15]中的优化结果，选取弧锥结合罩结构参数：药型罩锥角145°、弧度曲率半径0.8Dk(Dk为装药口径)、药型罩壁厚0.042Dk及装药高度1.1Dk。将弧锥结合罩锥角部分修改为喇叭形，并对大锥角喇叭罩顶点处倒圆弧，得到对应大锥角喇叭罩。为方便比较，增加相同罩顶高球缺罩作为对比。分别得到大锥角喇叭罩结构参数：喇叭曲率半径1.3Dk、弧度曲率半径0.36Dk、药型罩壁厚0.042Dk及装药高度1.1Dk；球缺罩结构参数：曲率半径1.1Dk、装药高度1.1Dk。3种药型罩结构方案如图1所示(单位mm)。

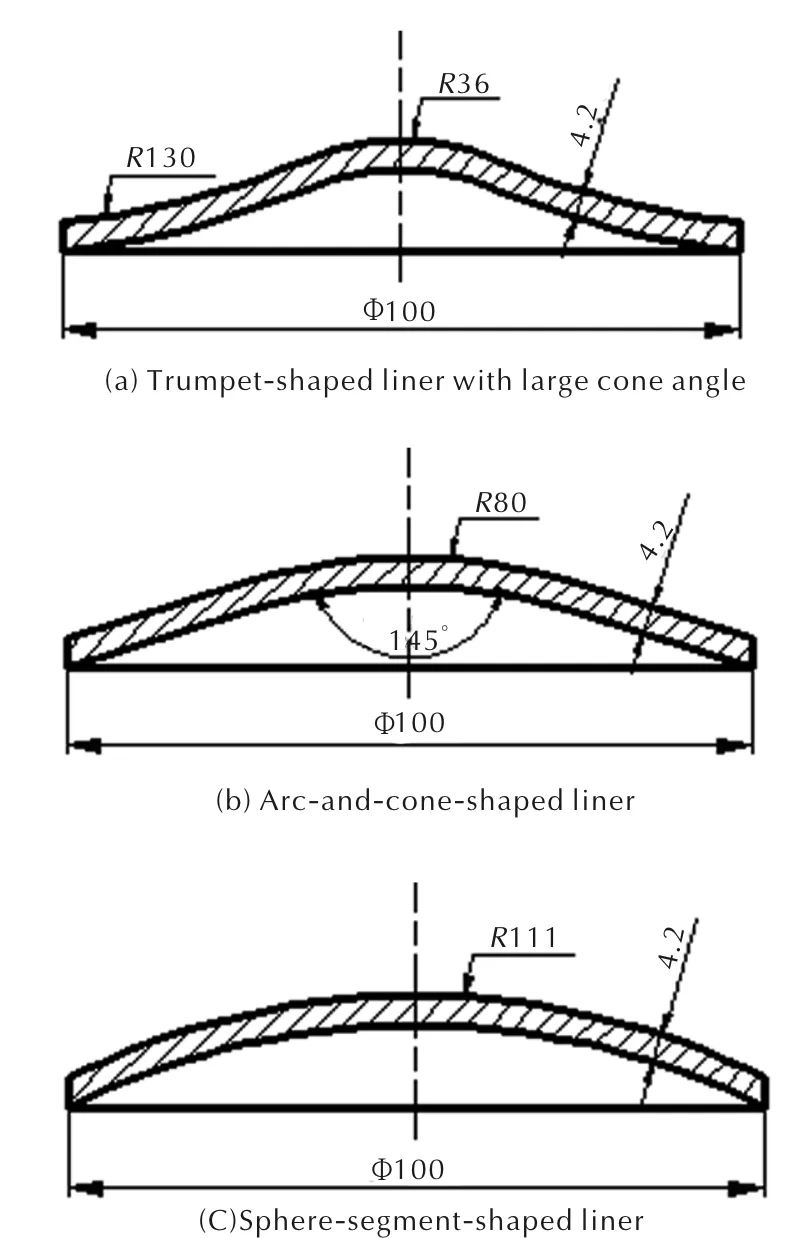
图1 3种药型罩结构示意图Fig.1 Cross-sectional view of three different liners

如图1所示，3种药型罩结构的罩顶高、罩厚一致，其中弧锥罩体积为32941mm3，大锥角喇叭罩体积为32941mm3，球缺罩体积为32913mm3，体积相近。

1.2 战斗部结构及计算模型

本研究采用船尾形装药结构，运用LS-DYNA 软件进行数值模拟，当药型罩为锥弧结合罩时对应的战斗部装药结构如图2 所示。装药口径(Dk)为100mm，装药高度(H)为110mm，采用装药底部中心单点起爆。采用ALE算法进行数值模拟，其中药型罩、炸药、空气选择多物质欧拉算法。药型罩材料为密度8.96g/cm3的紫铜，选择Johnson·Cook本构方程和Gruneisen状态方程进行描述；炸药为密度1.69g/cm3的8701炸药，其状态方程为JWL，本构关系为High_explosive_burn；空气选用Null本构方程和Gruneisen状态方程，计算中使用的材料具体参数见文献[15]。为避免压力在边界面反射，在整个空气计算域的外表面定义无反射边界。

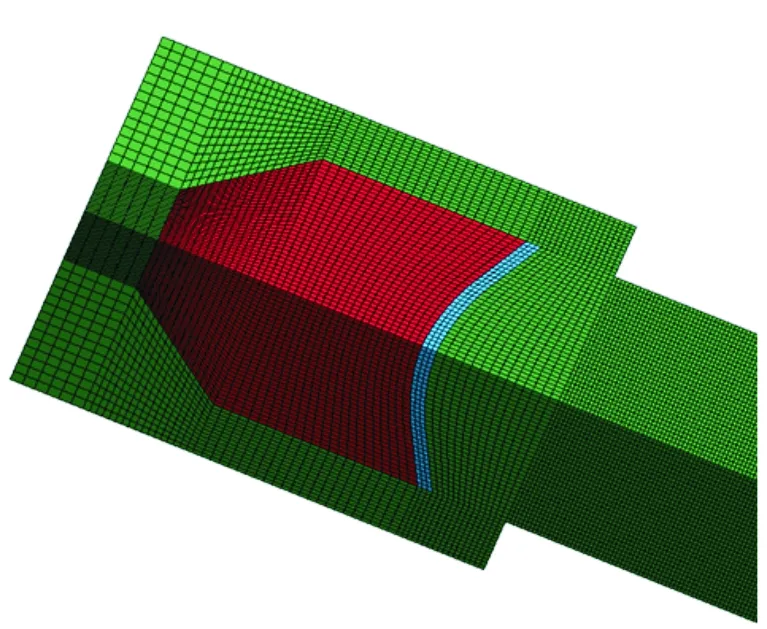
图2 EFP成型装药有限元模型Fig.2 Finite element model of EFP shaped charge

为方便对比，试验与数值模拟采用相同弧锥罩结构，结构参数为：R=0.9Dk，2θ=138°，T=0.038Dk，H=0.9Dk，中心点起爆。对此时刻下数值计算的EFP速度、长径比进行统计并与试验结果对比，如表1所示。

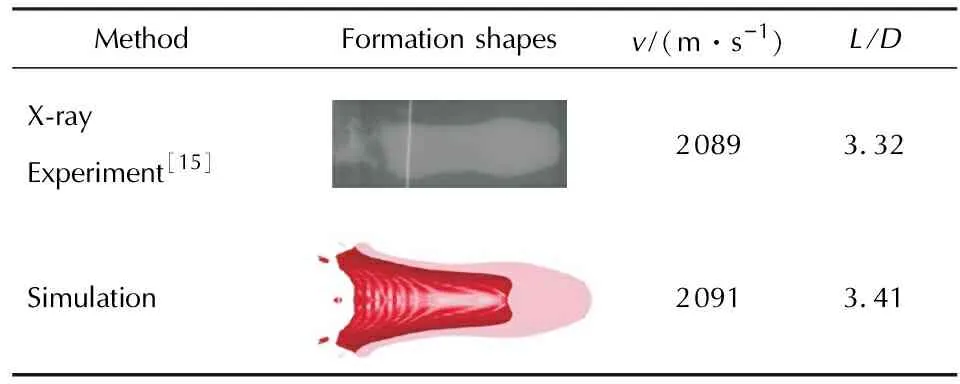
表1 弧锥结合罩EFP的X光试验与数值模拟对比(220μs)

注：v为速度；L/D为长径比。下表同。

由表1可以看出，此时的EFP头部较大，中部主体均匀，尾部出现一定断裂，数值模拟结果很好地反映了实际情况，准确性较高，因此可用来进行药型罩结构参数设计和EFP成型过程模拟。

2 结果与讨论

2.1 大锥角喇叭罩成型过程分析

利用数值模拟分别得到球缺罩、弧锥结合罩、大锥角喇叭罩下EFP的成型过程。3种药型罩均在180μs时刻形成了头尾速度较为一致的EFP，成型过程如图3所示。

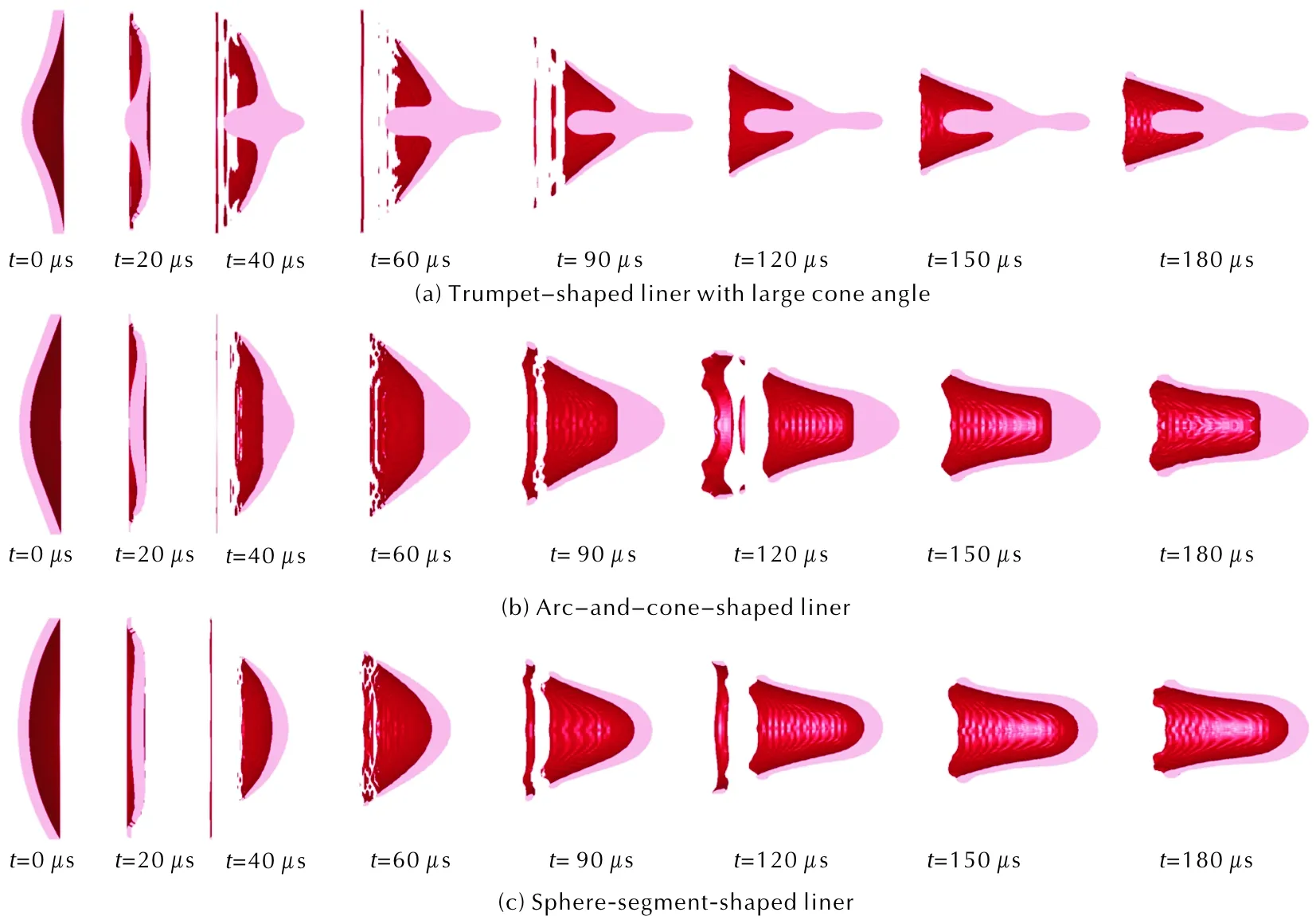
图3 3种药型罩EFP形成过程Fig.3 EFP formation process of three different liners

由图3可以看出，该参数下3种药型罩结构均能形成EFP结构，但3种结构具有显著区别：弧锥结合罩具有典型EFP特征，头部较为密实；球缺罩与弧锥结合罩类似，但由于成型以翻转为主，故头部密实度较低；而大锥角喇叭罩汇聚效应更为明显，密实度更高，但头部容易出现射滴。

为进一步分析3种药型罩对EFP成型的影响，假设爆轰波为平面波，将药型罩平均分为21块，用P来表示每一部分，划分方式以大锥角喇叭罩为例，如图4所示。分别得到3种药型罩与爆轰波间的夹角α，如图5所示。

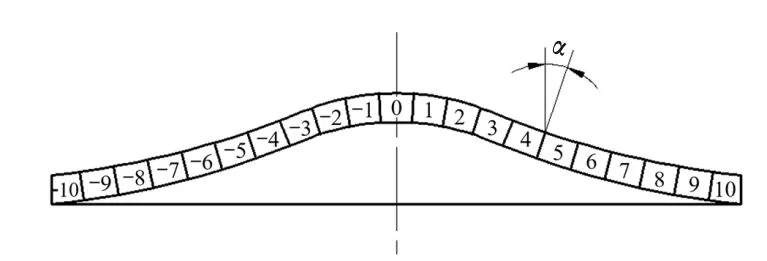
图4 大锥角喇叭罩结构划分示意图Fig.4 Cross-sectional view of trumpet-shaped liner with large cone angle

图5 3种药型罩与爆轰波间的夹角Fig.5 Angles between liners and detonation wave

由图5可知，3种药型罩与爆轰波的夹角可以分为两个部分，在罩的中间部分大锥角喇叭罩与爆轰波的夹角明显大于其他两种药型罩，导致径向压垮速度增大，由此汇聚效应体现的更为明显，药型罩在压垮过程中，头部一方面发生翻转过程，另一方面形成汇聚现象。该过程有利于EFP头部的延伸拉长，其药型罩质量在头部所占比例更多，可以有效提高药型罩的利用率，但如果控制不好，则很容易出现射滴现象，实际上会降低药型罩的利用率。根据图3所示，虽然弧锥结合罩与球缺罩均形成了向前翻转的EFP，但由于弧锥结合罩与爆轰波的夹角大于球缺罩，径向压垮速度高于球缺罩，故弧锥结合罩较球缺罩径向压合现象得到增强，其密实段长度更长。在罩的边缘部分，药型罩与爆轰波的夹角恰好相反，球缺罩由于罩边缘的圆弧特征，使其药型罩与爆轰波之间的夹角增大，导致径向速度增大、轴向速度梯度减小，更有利于尾裙形成。但考虑药型罩边缘处对EFP成型整体影响较小，且实际使用中壳体会进一步改变药型罩边缘处的成型过程，因此在EFP成型过程中罩中间部分受力情况对EFP成型的影响更为明显。3种结构药型罩EFP成型参数如表2所示。

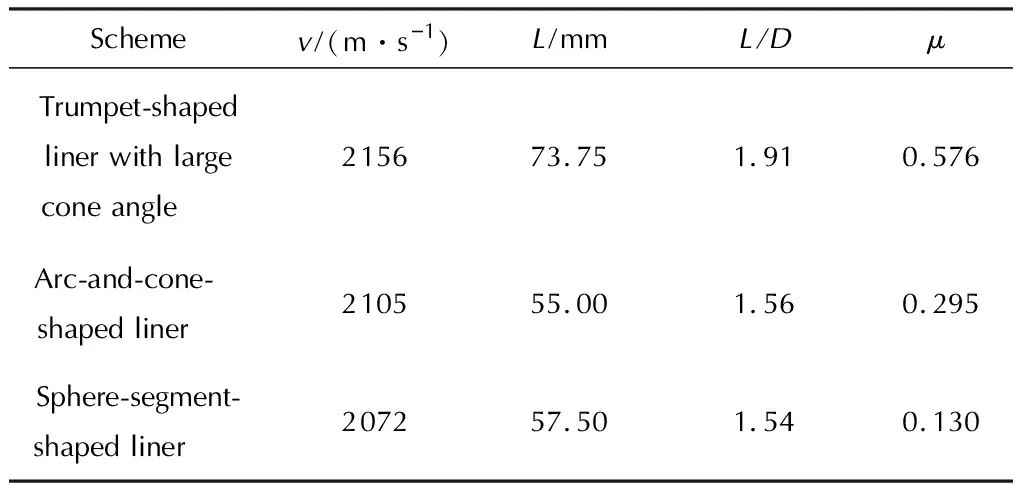
表2 3种结构药型罩EFP成型参数

由表2可知，大锥角喇叭罩在头部速度(v)、长度(L)、长径比(L/D)及密实度(μ)[16]方面均具有优势。相比弧锥结合罩和球缺罩，其总长度提高28%～34%，长径比提高20%以上，密实度提高1～3.5倍。且此时弧锥结合罩为较优结构，而大锥角喇叭罩尚未进行优化。为了找出一种密实度和长径比更大的EFP，同时解决EFP成型过程中容易形成射滴断裂问题，就需要研究大锥角喇叭罩的结构参数对EFP成型的影响规律，从中找出形成最佳EFP的结构参数。

2.2 大锥角喇叭罩结构参数的影响规律

对于大锥角喇叭罩结构，可以根据虚拟罩高和罩直径两点形成大锥角喇叭曲线，再对大锥角喇叭曲线进行倒圆，形成大锥角喇叭罩。这个过程涉及虚拟罩高(h)、喇叭曲率半径(R)、圆弧曲率半径(r)、罩厚(t)等4个独立参数，如图6所示。图中虚线为虚拟罩高可取范围，h′为实际罩高。

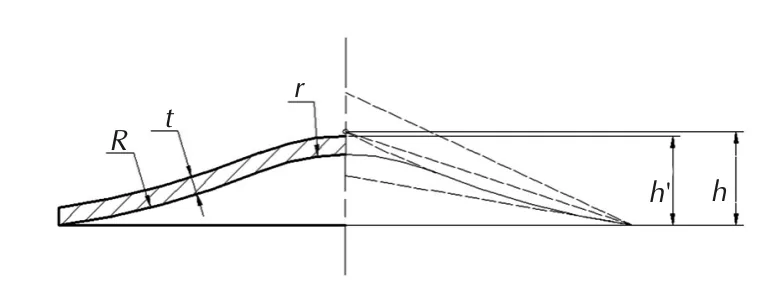
图6 大锥角喇叭罩结构示意图Fig.6 Schematic diagram of trumpet-shaped liner with large cone angle

为了进一步研究大锥角喇叭罩结构参数对EFP成型的影响，对大锥角喇叭罩结构不同参数的装药结构进行数值模拟，分别研究大锥角喇叭罩的虚拟罩高(h)、喇叭曲率半径(R)、圆弧曲率半径(r)、罩厚(t)等参数对EFP成型的影响规律。通常EFP成型参数主要包括飞行速度及长径比，但本研究的大锥角喇叭罩之前并未应用于EFP研究，其毁伤元成型特性或介于EFP与JPC之间，故主要研究毁伤元头部速度(v)、长度(L)及密实度(μ)3种参数对EFP成型的影响。

2.2.1虚拟罩高的影响

固定喇叭曲率半径(R)为1.35Dk，圆弧曲率半径(r)为0.4Dk，罩厚(t)为0.04Dk。由于要求药型罩形成EFP的锥角为130°～160°[17]，故取对应高度并等分，得到虚拟罩高(h)范围为0.09Dk～ 0.23Dk，分别取0.090Dk、0.125Dk、0.160Dk、0.195Dk、0.230Dk。通过数值模拟计算，得到200μs时刻各方案侵彻体成型参数及形态如图7所示。

从图7可以得到，侵彻体头部速度(v)随着虚拟罩高的增加呈先降后升的趋势，在虚拟罩高为0.14Dk～ 0.16Dk时头部速度最低，此时头部速度相较最高时低350m/s。随着虚拟罩高的增加，侵彻体头部明显拉长，总长度(L)、密实度(μ)均呈指数规律增加。当虚拟罩高达到0.16Dk～ 0.20Dk时，侵彻体逐渐成为杆式侵彻体，头尾开始具有显著速度差，有较为明显的射流和杵体部分，这是因为罩顶高度足够大，罩中心处更多位置与爆轰波间具有较大夹角，使被压垮的罩微元增加，故侵彻体拉伸更完全，其长度和密实度也更大。侵彻体速度的变化是由于虚拟罩高越小则药型罩越平缓，虽然径向速度分量减小而轴向速度分量增加，其翻转形成过程的轴向速度更高；虚拟罩高越大则药型罩头部压垮变形越多，其头部速度由初始轴向速度和压垮微元轴向合成速度构成，导致最终头部速度较高。而虚拟罩高介于两者之间时，其翻转过程的轴向速度较低且压垮效应不足，故速度处于整个阶段最低状态。

故对于大锥角喇叭罩，若要形成密实度好的EFP，则需要适当牺牲头部速度，虚拟罩高应取0.14Dk～ 0.16Dk。当虚拟罩高达到0.20Dk以上时，药型罩将形成杆式侵彻体。

2.2.2 喇叭曲率半径的影响

固定虚拟罩高(h)为0.16Dk，圆弧曲率半径(r)为0.4Dk，罩厚(t)为0.04Dk。当喇叭曲率小于某个值时喇叭线会外翻至罩外，故存在临界值，取临界值等分，得到该结构下喇叭曲率半径(R)范围为0.8Dk～ 4Dk，分别取0.8Dk、1.0Dk、1.35Dk、2Dk、4Dk。通过数值模拟计算，得到200μs时刻各方案侵彻体成型参数及形态如图8所示。

图8 侵彻体成型参数随喇叭曲率半径的变化曲线Fig.8 Changing tendency of the formation parameters of EFP along with curvature of trumpet-section liner

从图8可以得到，侵彻体头部速度(v)也随着喇叭曲率半径的增加呈先降后升的趋势，但整体变化幅度较小，不足100m/s。随着喇叭曲率半径的增加，侵彻体密实度(μ)变化不大，但总长度(L)趋于变长，形成的EFP更为均匀。喇叭曲率半径增加的过程也是罩顶高增加的过程，同样也是圆弧部占药型罩整体比例增加的过程。因此，喇叭曲率半径越大则药型罩整体与爆轰波的夹角也越大，药型罩所受径向压力越大，药型罩翻转形成的侵彻体成型也越修长，该过程同时伴有一定的压垮过程。值得关注的是，增大喇叭曲率半径可以避免EFP头部出现射滴，提高侵彻能力。

故对于大锥角喇叭罩，若要形成速度较高、密实度较好、成型效果较优的EFP，则可以通过增大喇叭曲率半径的方法得到，取1.5Dk以上喇叭曲率半径。

2.2.3 圆弧曲率半径的影响

固定虚拟罩高(h)为0.16Dk，喇叭曲率半径(R)为1.35Dk，罩厚(t)为0.04Dk。保证最小值具有加工性，最大值时趋于稳定，得到该结构下圆弧曲率半径(r)范围为0.1Dk～ 1.6Dk，分别取0.1Dk、0.2Dk、0.4Dk、0.8Dk和1.6Dk。通过数值模拟计算，得到200μs时刻各方案侵彻体成型参数及形态如图9所示。

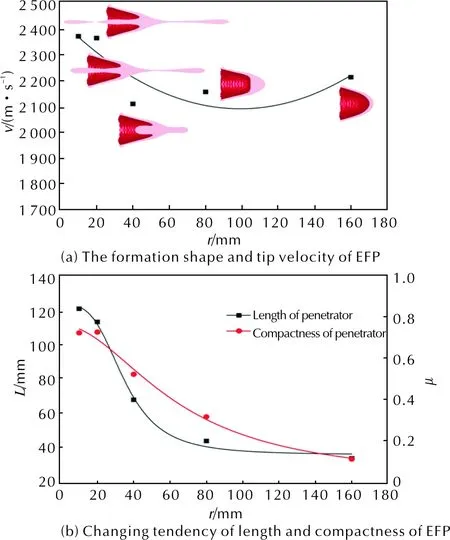
图9 侵彻体成型参数随圆弧曲率半径变化曲线Fig.9 Changing tendency of the formation parameters of EFP along with curvature of arc-section liner

从图9可以得到，侵彻体头部速度(v)同样随着圆弧曲率半径的增加呈先降后升的趋势，整体变化幅度约250m/s，当圆弧曲率半径为1Dk时速度最低。随着圆弧曲率半径的增加，侵彻体长度(L)和密实度(μ)均显著减小。值得注意的是，当圆弧曲率半径较小时，虽然侵彻体头部速度、长度和密实度均有所提高，但侵彻体形态较差，头部容易出现射滴，尾部具有明显杵体，严重影响侵彻能力。这是由于圆弧曲率半径越小则药型罩罩顶越高，喇叭曲线占整体药型罩比例也越高，而喇叭曲线的特点决定了罩中心处位置与爆轰波夹角较大，导致头部压垮速度较高而产生断裂。但是，若一味增大圆弧曲率半径也不利于侵彻体，此时形成的EFP虽然稳定，但呈现典型的馒头状形态，侵彻能力有限且不利于远距离飞行。

故对于大锥角喇叭罩，若要形成速度较高、密实度较好、成型效果较优的EFP，圆弧曲率半径不易过低但也不宜过高，取0.4Dk～ 0.8Dk较为理想。

2.2.4 罩厚的影响

固定虚拟罩高h为0.16Dk，喇叭曲率半径R为1.35Dk，圆弧曲率半径r为0.4Dk。根据相关文献[17]，取罩厚t范围为0.03Dk～ 0.05Dk，分别取0.030Dk、0.035Dk、0.040Dk、0.045Dk、0.050Dk。通过数值模拟计算，得到200μs时刻各方案侵彻体成型参数及形态如图10所示。

图10 侵彻体成型参数随罩厚变化曲线Fig.10 Changing tendency of formation parameters of EFP along with thickness of liner

从图10可以得到，侵彻体头部速度(v)随着罩厚的增加显著降低，整体变化幅度达到700m/s以上，影响巨大。随着罩厚的增加，侵彻体密实度μ变化不明显，长度(L)呈先增大后减小的趋势，罩厚在0.04Dk～ 0.045Dk下侵彻体长度较长。由侵彻体成型形态可知，罩厚变化对侵彻体形态整体影响不大，尾裙张角稍小，长径比稍大。罩厚对侵彻体成型的影响主要体现在头部速度方面。

故对于大锥角喇叭罩，罩厚通常可取0.04Dk～ 0.045Dk。但为了提高EFP飞行速度，可以在保证侵彻体所需质量的条件下尽可能降低药型罩罩厚，特别是对于某些高密度金属材料。

3 结 论

(1) 与传统弧锥结合罩和球缺罩形成的EFP相比，大锥角喇叭罩形成的EFP在头部速度、长度、长径比及密实度等方面均具有优势，在同质量的条件下，其总长度可提高28%～34%，长径比可提高20%以上，密实度可提高1～3.5倍。

(2) 侵彻体头部速度随着虚拟罩高、喇叭曲率半径和圆弧曲率半径的增加均呈先降后升的趋势，但对侵彻体头部速度影响最大的是罩厚，罩厚增加，头部速度显著降低。虚拟罩高和圆弧曲率半径则决定了侵彻体长度及密实度，侵彻体总长度和密实度随着虚拟罩高的增加呈指数规律增加，随着圆弧曲率半径的增加急剧减小。喇叭曲率半径的影响主要体现在侵彻体头部的成型状态，随着喇叭曲率半径的增加，侵彻体总长度趋于变长。

(3) 大锥角喇叭罩适用于EFP战斗部设计，通过对结构的调整可以得到适宜的EFP，成型较佳时各结构参数的取值范围为：虚拟罩高(h)取0.14Dk～0.16Dk，喇叭曲率半径R取1.5Dk以上，圆弧曲率半径(r)取0.4Dk～0.8Dk，罩厚(t)取0.040Dk～0.045Dk。