三维浅海下圆柱壳声辐射预报方法研究
2019-11-09钱治文何元安商德江
钱治文, 何元安, 商德江, 肖 妍, 史 博
(1. 天津大学 海洋科学与技术学院, 天津300072; 2. 哈尔滨工程大学 水声工程学院,哈尔滨150001; 3. 中国船舶工业系统工程研究院, 北京100036)
0 引 言
我国海洋领土大多属于水深小于200 m 的典型浅海环境, 潜器在浅海所处的声场环境并非理想的自由场,存在水面和水底的反射、散射作用[1],其声场特性与结构本身和浅海环境两者密切相关。 研究浅海下结构辐射声场特性,对开展浅海环境下结构振动辐射噪声实时监测预报、声学隐身性能评价以及浅海环境参数对辐射声场影响分析等研究领域具有重要的理论和应用价值, 是今后我国水声技术领域长期关注的热点和难点问题之一。
然而,目前关于水下弹性结构耦合振动与声辐射问题的研究,大多考虑无界或半空间流体域下的近距离辐射声场问题[2-3]。 对于浅海环境下结构辐射声场问题,国内外很少涉及该方面的研究,因该研究在试验法、解析法和数值法研究过程中均遇到了难题,有效开展工作较为困难;试验法周期长成本高,数值法受网格划分以及计算量的严重制约,解析解法目前只能针对理想浅海环境下简单结构声场问题[4-5]。为了解决浅海下弹性结构声辐射研究所遇到的这些难题,本文引入了一种对结构和流体环境适应性很强且计算高效的研究方法:波叠加法(Wave Superposition Method,简称WSM)。Koop-mann 等[6]最先提出了利用波叠加法进行结构辐射声场的计算,Miller 和Fahnline 等随之对稳定性、 计算精度和效率进行了分析[7-8]。波叠加法以适应性强、计算效率高的优势逐步地成为了研究弹性结构声辐射的重要方法之一,近年来受到了国内学者极大的关注,并广泛应用于自由场或半空间流体环境下的近场声全息[9-11]、结构声辐射预报[12-13]和噪声源识别[14-15]等研究领域。 但采用波叠加法进行浅海下结构声辐射的研究却很少,因为浅海下结构辐射声场问题涉及流体、结构和浅海上下边界等多个物理场之间的相互耦合作用,导致结构表面振动速度难以准确获取,从而无法进行波叠加法的准确计算。 也有部分研究把浅海下结构辐射源视为点声源,但这样直接忽略了结构与流体、结构与环境的耦合作用和近场声辐射特性。 导致目前尚无高效可靠的研究方法进行浅海环境下弹性结构声辐射预报的有效研究,但它对浅海下结构声辐射预报、源识别和噪声控制等具有重要的意义,急需探索一种新方法来解决浅海下结构声辐射预报问题[16]。
本文提出了一种三维浅海波导下弹性结构辐射声场预报的理论方法。 该方法首先利用有限元法建立了浅海波导下结构声辐射多物理场耦合有限元模型; 计算获取在考虑流体环境和浅海波导上下边界耦合影响下结构表面振动数据,然后采用波叠加法和浅海声场传输函数进行虚拟源源强求解,最后进行弹性结构辐射声场的等效叠加计算。 经有限元法和解析解法验证该方法的正确性后,研究了典型弹性圆柱壳在理想浅海波导下的辐射声场特性, 为今后开展复杂浅海环境下大型弹性结构声辐射预报研究提供了一种新途径。
1 理论模型
1.1 浅海波导下点源声传播模型
考虑声源为水下简谐点源,设海水为理想介质,压力p 满足非齐次亥姆霍兹方程

式中:▽2为拉普拉斯算符,c 为流体声速,r→为声源到场点的矢量距离,δ r→()为狄拉克函数,A 为点源强度幅值,j 为复数虚部,ω 为角频率。
由于声场具有圆柱对称性,选用柱坐标下,以通过点源且垂直向下的方向为z 轴,垂直于z 轴的方向为r 轴,方程可以写成[1]

式中:k0为流体介质中声波波数,定义为k0=ω/c,z0为声源在z 轴上的位置。
采用简正波理论求解式,可得浅海波导下点源声场表达式p (r, z )即浅海波导传输函数G (r, z )为
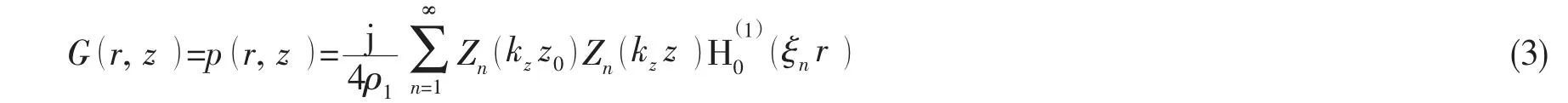
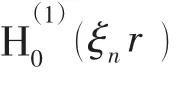
海面通常为Dirichlet 边界条件,满足的边界条件为

海底是一个反射和散射边界, 典型海底边界模型有Neumann 边界、Rayleigh 定律、Sommerfeld 模型、Cauchy 边界和地声模型等。
在Neumann 边界、Rayleigh 定律和Sommerfeld 模型的交互面上,满足声学边界方程为

1.2 波叠加法模型
建立如图1 所示的三维浅海下结构声辐射波叠加法计算理论模型,流体密度为ρ1,声速为c1;结构中心和点源在海面的投影为o 和o′,o-xy 和o′-x′y′与海面重合,o-xyz 为全局坐标系,o′-x′y′z′为各虚拟源的局部坐标系,oo′连线延长线为y′轴,o′y′与oy 的夹角为θ; 振动体表面记为S′,n 为结构表面的外法向矢量,zs为结构中心在竖直方向的位置;S 为与结构面共形的等效源面,Q 为虚拟源,z0i为各虚拟源在局部坐标中的位置;P 为场点位置,Q 和P 间的距离记为rp。

图1 三维浅海波导下波叠加法原理示意图Fig.1 Principle of wave superposition method in three-dimensional shallow water waveguide
波叠加法与Helmholtz 积分公式等效,经过离散化处理后,全局坐标系下结构表面某一点的法向速度un可由N 个简单声源构建[18]
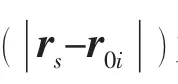
把(7)式写成矩阵形式,可表示为

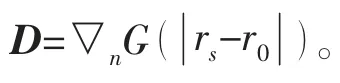

其中,[D]-1为[D ]的广义逆矩阵。
为了求解传递矩阵的广义逆[D]-1,需要对其进行奇异值分解

式中:S、V 分别为M 阶、N 阶方阵,Σ=diag (σ1, σ2, σ3…σn)为包含n 个非奇异值σi的对角阵。
通过奇异值分解求逆矩阵获取辐射体结构内部虚拟源源强后,便可计算任意一点的声压

从(9)式和(11)式可知,传递矩阵D 和单极矩阵T 中涉及的传递函数G (x, y,z )均为全局坐标下三维声场传递函数,而1.1 节求解的声场传递函数为局部柱对称坐标下二维声场传递函数G (r, z ),需要进行如下空间坐标转化。
浅海下各虚拟源产生的空间声场满足轴对称性, 三维局部坐标系o′-x′y′z′下声场可降为二维轴对称局部坐标系o′-rz′下声场,根据局部二维坐标下各点源到场点水平距离r 和竖直距离z′求解各点源对场点的声场作用G (r, z′ )即G (x′ , y′, z′ )(其中x′=rcosϑ,y′=rsinϑ,ϑ 为r 轴与x 轴夹角),然后通过局部坐标系与全局坐标系的转换关系建立各点源在全局坐标系下的声场作用G (x, y,z )。首先将局部坐标系声场函数G (x′ , y′, z′ )沿x 方向、y 方向和z 方向分别平移Δx、Δy 和Δz, 得到全局坐标系下声场G (xi, yi, zi),平移变换矩阵为

然后再将全局坐标系下声场函数G (xi, yi, zi)绕z 轴顺时针旋转角度θ, 得到与全局坐标系o-xyz下的声场函数G (x, y,z ),旋转变换矩阵为

通过局部坐标o′-rz′到全局坐标o-xyz 的转换, 可求得各局部坐标下点源声场函数G (r, z′ )对全局坐标系下结构表面的作用G (x, y,z )。
由(9)式和(11)式可知,该方法计算的基本思路为:首先通过有限元法建立浅海波导下弹性结构声辐射数值模型,计算获取结构表面法向速度U,然后通过波叠加法以及传输函数G 进行虚拟源源强Q 求解,最后结合单极矩阵T 便可计算在任意场点的辐射声场P。
2 数值分析
2.1 方法准确性与高效性分析
如图2 所示,建立了浅海波导下脉动球有限元模型,波导深度h=50 m,海面为Dirichlet 边界,海底为Neumann 边界,流体四周无限大边界。 小球中心深度为zs=25 m,半径为r0=3 m,表面施加均匀振速ua,数值计算获取表面振动数据,然后采用波叠加法计算场点声场信息。
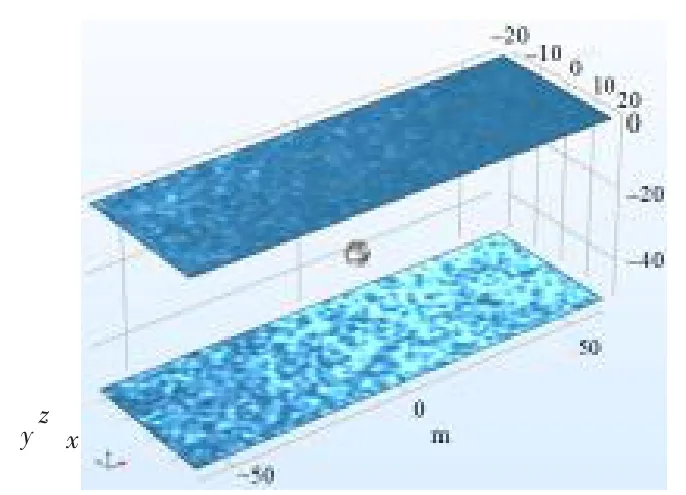
图2 浅海波导下脉动球声辐射有限元模型Fig.2 The finite element model of spherical shell in shallow water waveguide
如图3 所示, 利用本文浅海波导下辐射声场波叠加计算式即(11) 式计算了浅海波导下脉动球辐射声压级随距离的变化曲线(各场点深度为h2=30 m),并分别与解析解法即(14)式、有限元法计算结果进行了对比分析,验证了该方法计算声场的可靠性。

图3 波叠加法计算结果验证Fig.3 The verification of wave superposition method
图4 FFP 与Kraken 计算结果对比Fig.4 The comparison between FFP and Kraken
虽然采用简正波法存在一定的近场声场计算精度问题, 但从远场波叠加法声场计算结果验证来看,其计算精度是满足要求的。为了说明采用简正波法的声场波叠加计算精度问题,本节采用最为精准的波数积分法计算程序FFP 与简正波计算程序Kraken 进行了计算结果对比分析。 计算环境以Pekeris波导为例,海水密度ρw=1 024 kg/m3,声速cw=1 500 m/s;半无限液态海底密度ρw=1 800 kg/m3,海底声速cw=2 500 m/s;海水深度h=200 m,声源深度zs=100 m,接收点深度zr=50 m,如图4 所示,分别采用FFP 和Kraken 计算了点源在浅海波导内的传播损失曲线对比图。
从图4 可知,采用简正波法与波数积分法计算结果在近场存在一定偏差,且波数积分法计算结果更为准确,当达到一定距离后,两者的计算结果基本吻合。 但因简正波的推导简单, 低频计算效率高,所以本文采用简正波进行波叠加法中声传输函数的求解,且声场波叠加法计算精度也是满足要求的。 为了进一步完善浅海下结构声辐射预报理论体系,提高波叠加法计算精度,后续将通过从波数积分法改进浅海波导声传输函数、优化结构表面测点和虚拟源布放方式进行深入研究。

表1 不同距离范围声场计算时间Tab.1 The calculation time of different distance range
为了显示该方法在进行浅海波导下弹性结构辐射声场计算方面的高效性, 以下采用该方法对不同计算距离范围进行了时间测试,如表1 所示。
从图3、图4 和表1 可看出,该方法计算结果不仅与解析解法、有限元法计算结果吻合很好,而且计算效率高,能够快速准确进行浅海波导下任意结构辐射声场预报。
2.2 典型浅海波导下圆柱壳声辐射分析
建立如图5 所示的理想浅海下弹性圆柱壳声辐射多物理场耦合有限元模型,浅海深度h=50 m,海面为Dirichlet 边界,海底为Neumann 边界。结构为弹性圆柱壳,半径a=3 m,长度l=30 m,厚度d=0.01 m,材料为钢(密度ρs=7 850 kg/m3,杨氏模量Es=2.05×1011Pa,泊松比us=0.28),圆柱壳中心距水面为25 m,在圆柱壳中间施加径向简谐力Fr=1 000 N,结构边界为自由边界,h2为圆柱壳轴线方向上各个场点距离水面的距离。
图5 浅海波导下结构声辐射模型Fig.5 Acoustic radiation model of structure in shallow water waveguide
首先采用有限元法对浅海下弹性圆柱壳声辐射进行建模计算,获取了圆柱壳表面附近192 个测点的振动数据。根据文献[18]虚拟源布放建议,在离散的结构内部空间均匀布放162 个虚拟源,虚拟源源面为与弹性结构共形的圆柱面,其中虚拟圆柱面长为24 m,半径为2.4 m。 通过(9)式计算虚拟源源强后,采用(11)式计算了各个虚拟源在任意场点的叠加声场。 等效计算弹性结构辐射声场后,便可研究浅海下弹性圆柱壳辐射声场特性。
2.2.1 远距离声辐射曲线
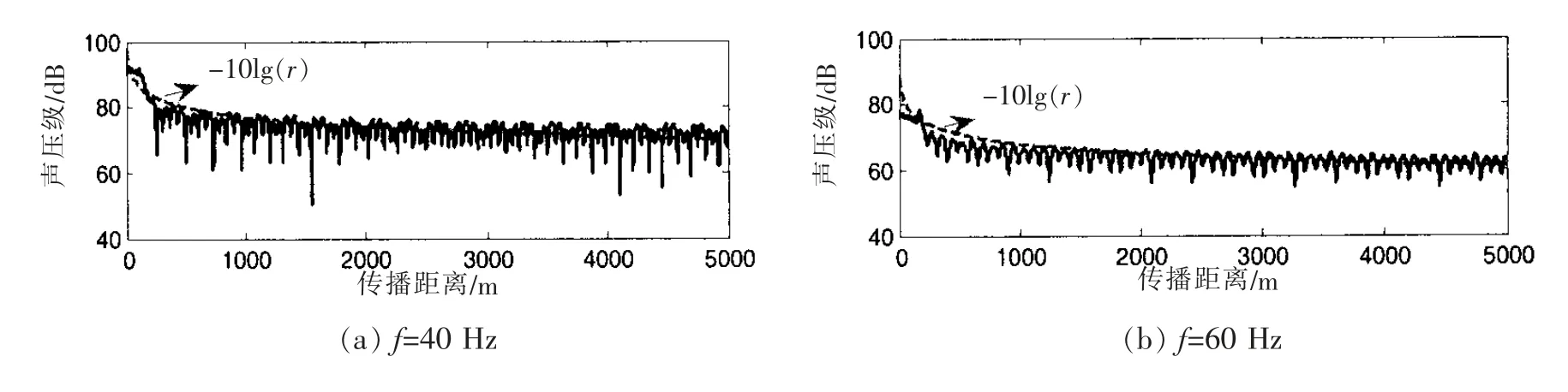
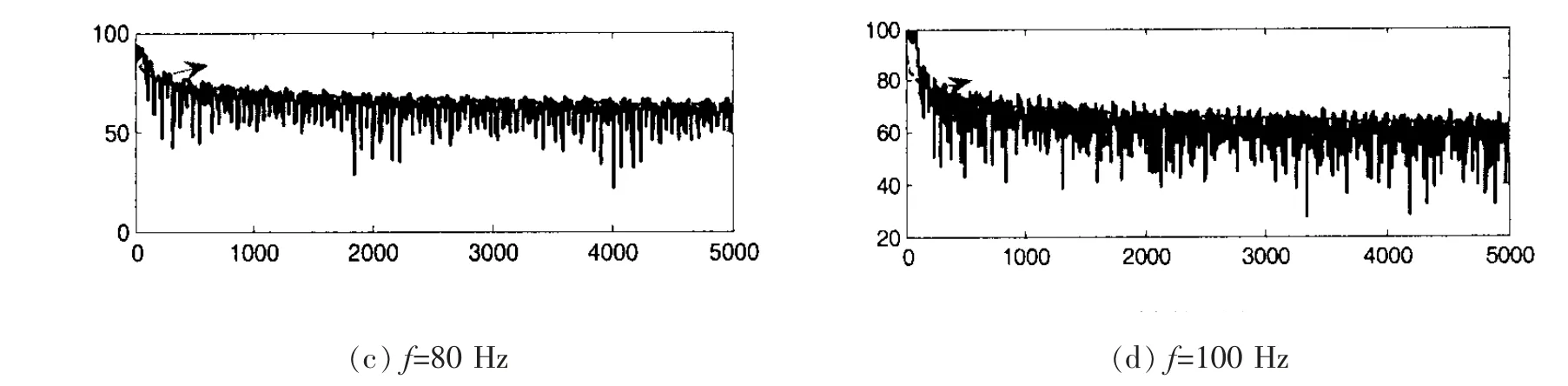
图6 不同频率的辐射曲线Fig.6 Radiation curves at different frequencies
采用图5 所示的有限元数值模型计算获取圆柱壳结构在典型浅海波导下的圆柱壳表面振动数据,再通过波叠加法和浅海波导传输函数计算浅海下任意场点的声场信息。 如图6 所示,分别给出了浅海波导下弹性圆柱壳不同频率所对应的辐射声压级随水平距离变化曲线, 各场点连线与圆柱壳轴线平行,各个场点的深度取为h2=30 m。在结构近场附近,辐射声场受到结构尺寸影响较大,辐射声压级曲线变化较为复杂。 由于场点声场受到浅海波导上下界面的干涉叠加影响, 圆柱壳在整个距离上的辐射声场发生了相长和相消的叠加,声压级曲线波动明显。 但当场点距源中心达到一定距离后,辐射声场受结构尺寸影响较小,其辐射声压级衰减规律按柱面波即满足-10lg(r)衰减。 因整个声场计算是由多个虚拟源产生声场叠加而来的,所以总声场的波动规律相对于单个点源声场波动细节较多。 在近场,场点与各个虚拟源之间距离的大小相差较大,导致在采用(11)式进行声场计算时,所涉及的单极矩阵T 相差也较大,即进行了不同相位和幅度的声场叠加计算,导致结构近场辐射声场波动比较复杂。 在远场,由于场点距虚拟源的距离远大于各个虚拟源之间的距离,各个虚拟源与场点之间的距离相差较小,所以各虚拟源在场点产生声场近似为同相叠加,叠加的总声场波动规律较为稳定,声压级按-10lg(r)递减规律进行衰减。
2.2.2 空间声场分布
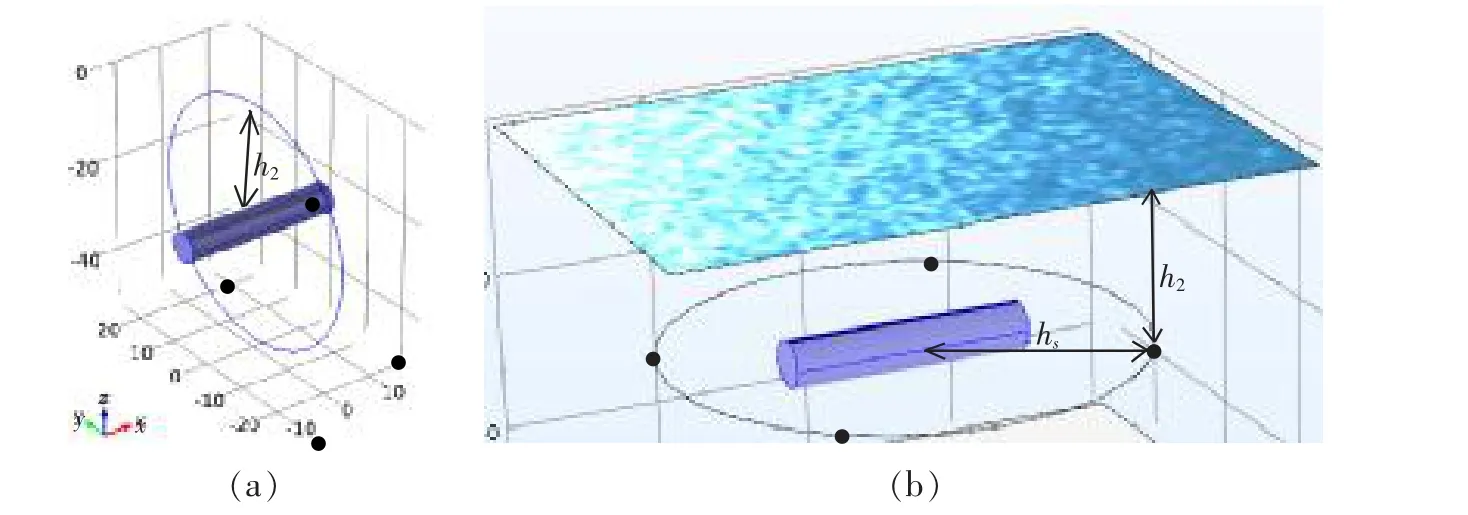
图7 空间场点选取示意图Fig.7 The diagram of space field selection
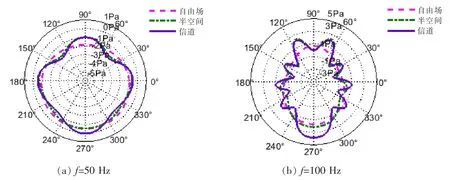
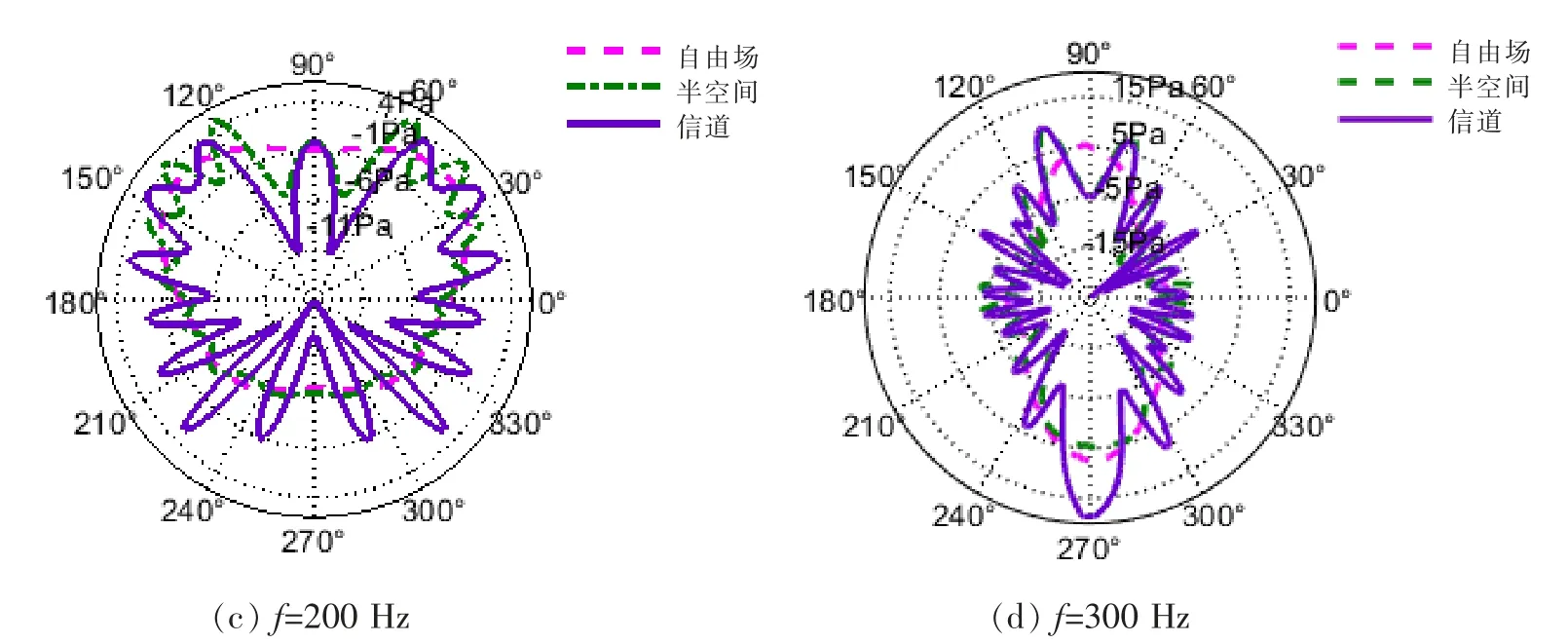
图8 不同流体环境下辐射声压对比Fig.8 The comparison of sound pressures in different fluid environments
为显示圆柱壳在垂直方向上的近场声场分布特性,按图7(a)所示的场点选取方式(场点选择在距离结构中心h2=25 m 的圆周上,圆周所在平面垂直圆柱壳轴线,极角90°和270°处分别对应浅海海面和海底),利用波叠加法计算了50 Hz、100 Hz、200 Hz 和300 Hz 频率下,圆柱壳辐射声压在不同流体环境中的空间声场分布,并分别与相同条件下圆柱壳在自由场、半空间流体环境中计算结果进行比对分析,如图8 所示。通过对比三种流体环境下辐射声场空间分布可看出, 边界的存在会使在靠近边界处的声场分布出现较大波动,浅海波导下结构辐射声场由于同时受浅海波导上下界面的影响,在深度方向上声场为驻波场,各个驻波干涉叠加导致在整个圆周上均出现明显的旁瓣。 在不同频率时,下界面和上界面对整个圆柱壳辐射声场分布影响作用不同,如当频率为200 Hz 时,在上半圆周上的声场分布已经受到了浅海下边界反射声的严重影响,而不会出现在其他频率如50 Hz、100 Hz 和300 Hz 时,浅海和半空间环境下辐射声场在上半圆周的声场分布情况趋于一致。 相对于较高频率,根据简正波理论[1],50 Hz频率下在深度方向上只有3 阶简正波且对应波长较长, 声场干涉不明显, 辐射声压空间分布波动较小,在竖直方向上的空间分布曲线类似为圆形。 随着频率的增加,在深度方向上的简正波数目和声场波动细节增加,辐射声压空间分布曲线的旁瓣数量增加。 而由于浅海下场点声场由不同成分的反射声与直达声干涉叠加构成,结构在浅海下叠加的总声压幅值均大于自由场以及半空间下的声压幅值。
图9 为在水平面上选取了不同深度场点下的辐射声压级(单位:dB)空间分布,场点选取如图7(b)所示,场点在水平距圆柱壳中心hs=1 000 m 处的水平圆周上,各场点距离水面距离为h2,极角0°和90°处分别对应圆柱壳端面与侧面。 可看出,在水平方向上,界面反射声对圆周上各个场点的影响作用相同,所以声场分布特性主要与结构本身的辐射声场相关。 在低频段时,结构辐射声场指向性分布不明显,且结构在水平方向的辐射声场为扩散声场,无驻波的干涉作用。 频率为30 Hz 时,圆柱壳在不同场点深度下的空间声场分布均为圆形,说明在30 Hz 处的辐射声场可等效为单极点源声场,而其他频率下声场空间分布特性在不同场点深度下会出现明显的分布差异,结构源不可等效为点源。
2.2.3 简正波模式分析
浅海波导下圆柱壳辐射声场受到了浅海上下界面的限制,在深度方向存在简正波。 为了研究驻波中简正波模式对圆柱壳声辐射的影响, 图10 分别计算了60 Hz 频率下只保留1 个、2 个、3 个和4 个简正模式((3)式中n=1, 2, 3, 4)的圆柱壳声辐射曲线。 由(11)式可知,圆柱壳在任意场点的辐射声场是由多模式叠加作用的结果,随着简正波模式的增加,圆柱壳声辐射曲线的细节也在增加。
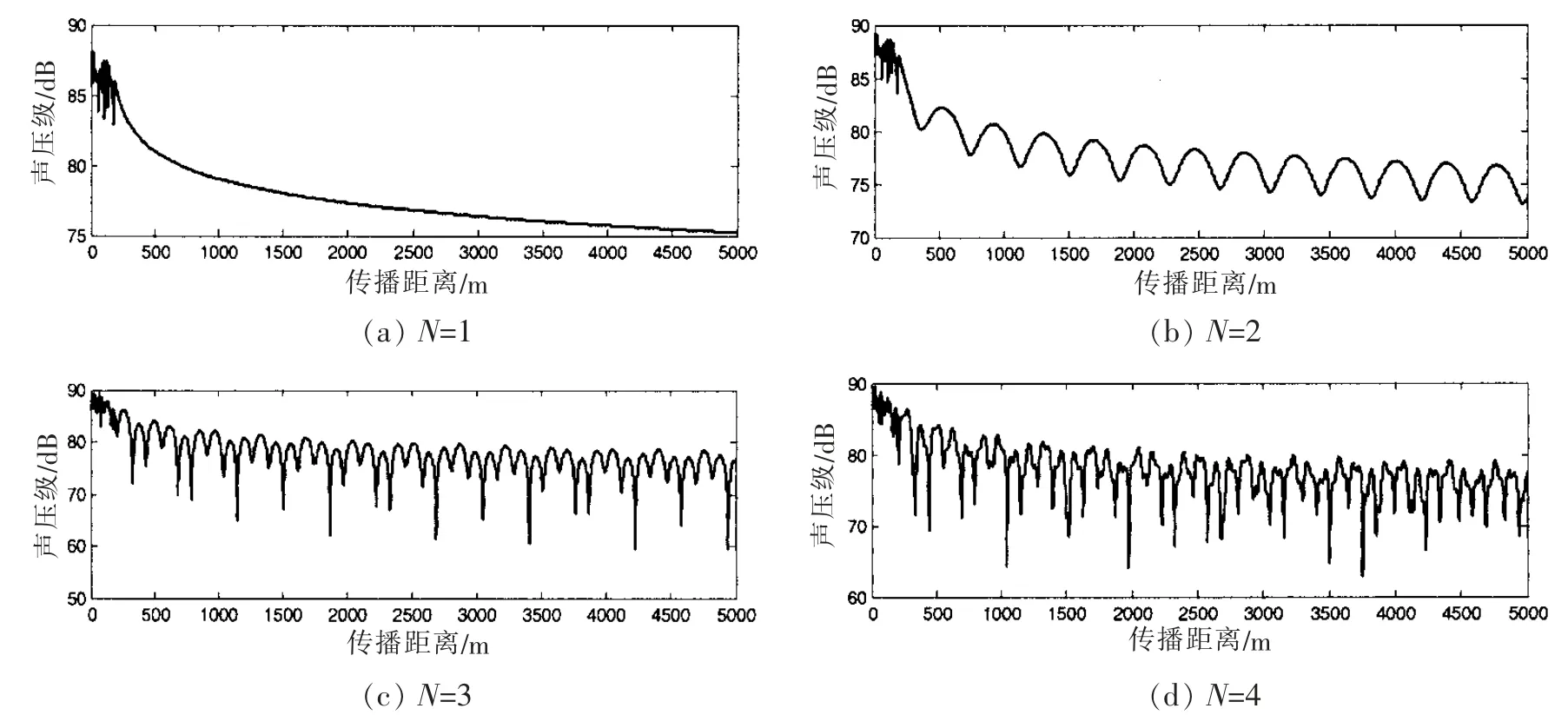
图10 不同简正波模式的辐射曲线Fig.10 Radiation curves at different normal modes
为了分析各模式辐射声场特性,可以把浅海下声场传输函数((3)式)表示为简化的声强形式
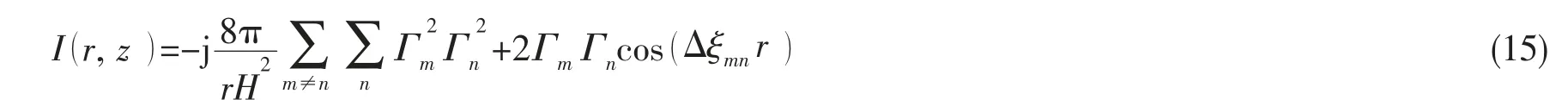
当采用(11)式进行结构声辐射声场计算时,在传输函数G(r, z)中只保留一个模式,复声压包含振荡项ejξrr,包络曲线是平滑的;保留两个模式时,声强包含了cos [(ξr1-ξr2)r ],声辐射曲线出现了波动,而且干涉曲线的重复尺度远大于该频率下的波长;当G(r, z)保留3 个以上的辐射模式,声强表达式包含的级数项进一步增多,干涉结构的复杂性加大。
3 结 论
本文采用WSM 进行了三维理想浅海下弹性圆柱壳辐射声场特性的研究,主要结论如下:
(1) 在近距离处,浅海波导下圆柱壳各频率所对应的声辐射曲线受结构尺寸影响较大,声场分布较为复杂;在远距离处,由于结构尺寸对声场影响减小,辐射声场波动规律稳定,按柱面波扩展规律波动,即辐射声压级随水平距离r 的变化按-10lg(r)进行扩展。
(2) 在竖直方向空间声场分布上,由于声场受上下界面影响,辐射声场为驻波场。 浅海波导下的声场分布不同于自由场以及半空间下声场分布,其声场分布差异随着频率的增加而增大;在水平方向的空间声场分布上,辐射声场为扩散场。 且在低频处(如本文分析频段30 Hz 处),远场圆柱壳空间声场分布可等效为无指向性点源声场,而其他频率下辐射声场出现明显的指向性分布,不可等效为点源声场,必须以圆柱壳作为实际辐射源进行声场计算,以获取其真实的声场分布特征。
(3) 结构内部某一虚拟源在场点的声场是由各个模式简正波叠加计算获取的,且不同简正波模式下的叠加数目不同,导致最终结构辐射声场波叠加计算的干涉曲线波动规律不同,随着传输函数中简正模式的增加,辐射曲线波动细节增多,波叠加法的计算结果更为精确。
