基于后艉轴承变位的某轴系试验台校中及回旋振动优化

赖国军， 刘金林， 曾凡明， 蔡耀全

（海军工程大学 动力工程学院， 武汉430033）

0 引 言

船舶推进轴系的振动与校中问题一直以来都是船舶领域研究的热点， 因其直接关系到船舶安全和可靠运行。 轴系[1]的主要作用是将主机发出的功率传递至螺旋桨，驱动螺旋桨旋转，再将螺旋桨旋转产生的推力或拉力通过推力轴承以轴承力的形式传递至船体，从而驱动船体的前进后退。 轴系在运行过程中，承受着多种相互影响的载荷作用，其校中质量直接影响到各轴承承受载荷的情况。 若校中不良可能引起个别轴承上的载荷过大、异常磨损严重从而影响船舶的安全、可靠和稳定的运行，同时也可能诱发异常的振动和噪声，影响船舶的声隐身性能。 国内外许多学者和相关研究机构已在船舶轴系的校中优化和减振降噪领域做了一定研究，用于指导工程实践并取得了较好效果。

在轴系校中优化研究方面，主要开展了直线校中、按轴承允许负荷校中、合理校中以及动态校中等研究工作。 大连海事大学魏海军等采用传递矩阵法研究了后艉轴承的多点支撑问题；武汉理工大学周瑞平等研究了轴系校中计算的三弯矩法和有限元法； 中国船员陈海兵分析对比了轴系静态校中的几种方法，并研究分析了轴端加工误差、船体变形和法兰下垂等对轴系校中质量的影响，等等。 在轴系回旋振动的减振降噪的研究方面，目前一般采用调频法、减小振源激励和隔振的方法。 Stankin 大学的Logr.zverv 等人[2]通过建立轴承有限元模型，提出了内置球轴承刚度计算模型，采用数值运算的方法研究了轴承刚度对轴系回旋振动的影响，但在研究过程中忽略轴承水平刚度和竖直刚度的不一致，导致轴系回旋振动在水平和竖直方向的计算结果与真实值存在一定的差别； 哈尔滨工程大学的周海军等人[3]研究了一种适用于弹性支撑、变轴颈和多跨距轴系回旋振动计算方法-改进傅立叶级数方法，研究轴系回旋振动与轴承支撑特性间的关系；武汉理工大学的朱军超、朱汉华等人[4]通过建立轴系回旋振动模型，分别考虑了陀螺效应、外加冲击载荷、中间轴的安装位置、轴承支撑刚度、后艉轴承上的有效接触长度和船体变形引起的轴系中心线垂向位移等对轴系回旋振动的影响，等等。 据查阅相关文献[5]可知， 很少有学者研究在轴系校中设计阶段通过调整各轴承位置来同时优化轴系校中和减小轴系的振动，特别是短轴系一般只考虑采用直线校中方法。

本文以某电机驱动轴的轴系试验平台为研究对象，在研究其直线校中计算的基础上，求得其负荷影响系数，以后艉轴承上负荷最小为目标得到其合理校中结果。 在轴承变位范围内（-10 mm，10 mm），调整后艉轴承竖直方向位移以步长为1 mm，并计算该轴系试验平台在不同校中状态下的回旋振动特性，再根据查阅相关文献建立轴系校中质量和回旋振动的权重系数，寻找合适的后艉轴承变位以获得较理想的轴系校中和横向减振结果。

1 某轴系试验平台简介

某电力推进轴系试验平台如图1 所示。

图1 轴系试验平台布置简图Fig.1 Sketch of shafting testing platform arrangement

该轴系试验平台主要的组成部件有螺旋桨（用圆盘代替，装设有径向和轴向加载装置）、艉轴、后艉轴轴承、前艉轴轴承、中间轴、半联轴器、推力轴承、高弹联轴器、齿轮箱和电机等。其中，艉轴由前、后艉轴承支撑，推力轴由推力轴承支撑，艉轴与中间轴通过半联轴节连接，中间轴与推力轴之间通过法兰连接。 本轴系试验平台中的前、后艉轴承都是水润滑，推力轴承是滑油润滑。 在本文中考虑轴承润滑特性时，为便于叙述，将各轴承统称作油膜润滑，但在计算时分别对润滑液体的不同属性做了不同处理。

2 轴系试验平台校中计算及优化

轴系的实际受力情况十分复杂，在进行校中计算之前，需要将轴系实验平台的物理模型简化为合理的数学模型，并在简化处理过程中作一些合理的假设。

模型简化:将该轴系实验平台从螺旋桨末端到电机输出端简化为敷设在多个铰支承上的连续梁，每个轴承处设一个实支撑、截面变化处设一个虚支撑，螺旋桨悬臂梁作用用集中载荷代替。 根据上述假设，得到该轴系试验平台的校中简化模型如图2 所示。

图2 某型轴系试验平台简化模型Fig.2 Sketch of the shafting testing platform

2.1 轴系试验平台校中有限元建模

根据该轴系试验平台的相关参数， 参考相关文献对它们进行处理并采用Beam188 单元建立其有限元[6-8]模型。弹性模量E=2.1E11 N/m2，泊松比μ=0.266。在ANSYS 中定义轴系的材料属性和截面参数后创建有限元模型，并划分网格。 根据几何数据建立ANSYS 有限元模型，建模的原点设置在轴系螺旋桨末端，轴系沿X 轴方向布置，Y 轴方向为竖直方向，Z 轴为水平方向。 在ANSYS 中重力方向是向上的，故设置加速度为Y 向-9.8 m/s2，如图3 所示。

图3 轴系有限元模型Fig.3 Finite model of the shafting

2.2 轴系试验平台直线校中计算

由2.1 节可得根据该轴系试验平台实际尺寸在ANSYS 中建立其三维模型，并划分网格，将轴系离散为有限个细长的Beam188 梁单元，Beam188 梁单元模型如图4 所示。

在轴系试验平台直线校中计算过程中，每个梁单元包括两个节点，相邻两单元通过节点相连并且单元之间的力和力矩都是通过节点实现传递的。 由图4 可知节点处所受到的剪力（Qi, Qj）和弯矩（Mi, Mj）情况。

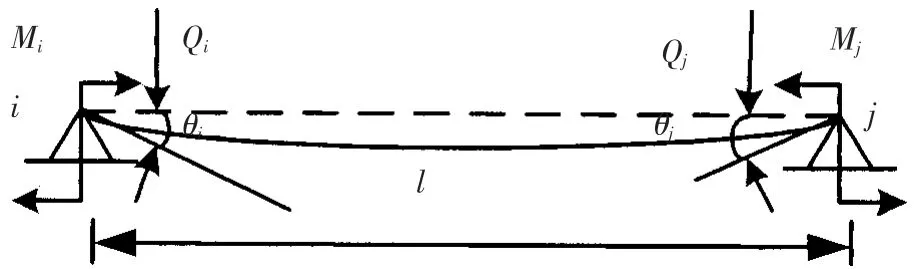
图4 Beam188 梁单元模型Fig.4 The mode of element Beam188

该梁单元所受剪力向量｛Q｝e和形变向量｛δ｝e分别为:

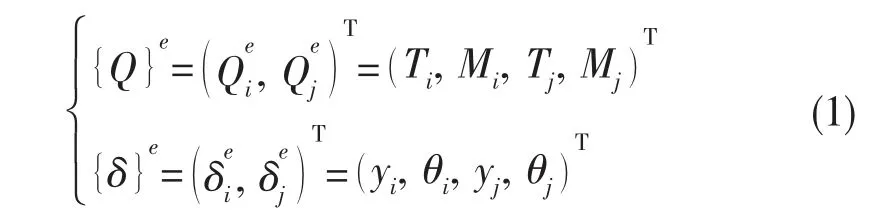
式中:Ti，Tj为节点i、 j 上的剪力；Mi，Mj为节点i、 j 上的弯矩；yi，yj为节点i、 j 沿Y 轴（竖直方向）的位移；θi，θj为节点i、 j 绕X 轴（轴向）的转角。

轴系校中时，轴系变形均在弹性变形范围内，受力与变形之间为线性关系:

式中:Ke为单元刚度矩阵。

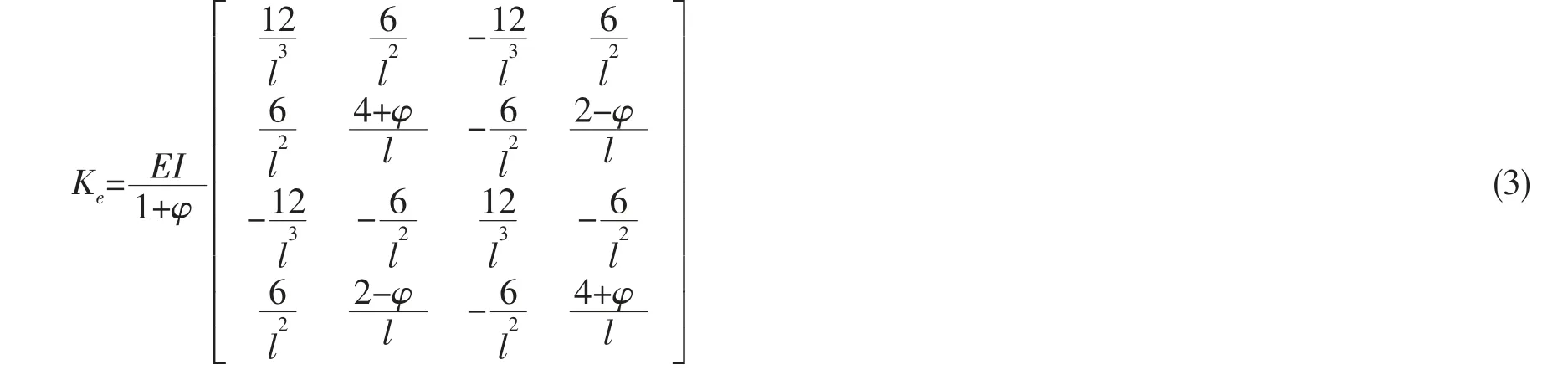
联立（1）-（3）式可求得轴系每一个梁单元的刚度矩阵，将各单元的刚度矩阵重新组合即可得到该轴系试验平台的刚度矩阵K，轴系形变δ 与所受载荷R（集中力和弯矩）之间的关系函数为:

轴系直线校中时，各轴承变位δi=0，经静态校中计算得到轴系直线校中各轴承的状态如表1 所示。该轴系试验平台直线校中状态下的弯矩和剪力情况分别如图5 和图6 所示。 由轴承负荷影响系数的相关定义[9]，再结合该轴系直线校中计算结果可知该轴系的轴承负荷影响系数（Aij）为

表1 轴系直线校中各轴承的状态Tab.1 Conditions of each bearing under shafting linear alignment

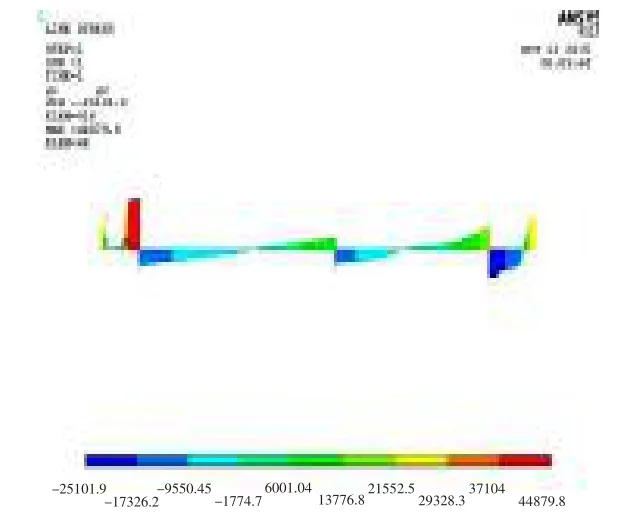
图6 直线校中状态下的剪力Fig.6 Shearing under shafting linear alignment

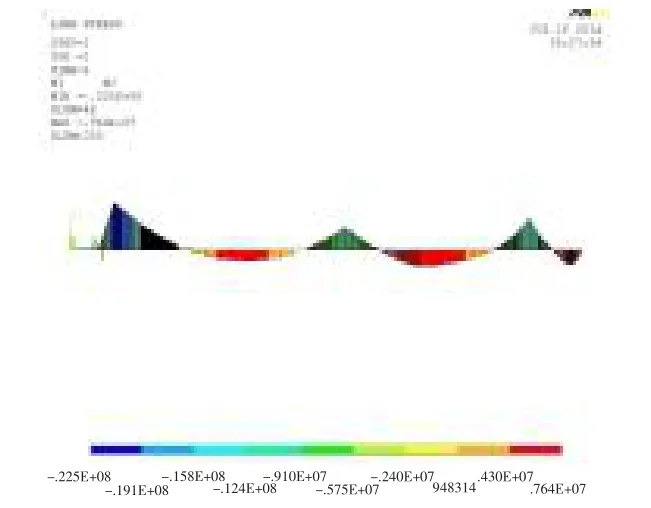
图5 直线校中状态下的弯矩Fig.5 Moment under shafting linear alignment

由表1、图5 和图6 可知，该轴系试验平台在直线校中状态下，由于螺旋桨悬臂梁作用，造成后艉轴承处的挠度变形、弯矩和转角都大于轴系的其他位置；后艉轴承和推力轴承处轴段转角超过许用范围（大于3.5E-04 rad），需要采用开斜镗孔的方式加以改善；前、后艉轴承上的载荷差值较大，易引起后艉轴承的异常磨损，需要调整各轴承的变位以减小后艉轴承上的载荷。

2.3 轴系试验平台校中优化

由2.2 节直线校中计算结果可知，由于螺旋桨的悬臂梁作用，造成后艉轴承的载荷过大，易导致后艉轴承的异常磨损和轴系横向激励过大。 因此，在优化轴系试验平台校中优化时，需调整轴系试验平台各轴承的竖直方向（Y 向）变位，以后艉轴承上载荷R1最小为目标函数，其他轴承上的载荷在允许范围内且相邻两轴承上的载荷差最小。 轴系各轴承变位后R1可表示为

式中:R0i为轴系直线校中状态下各轴承上的载荷（kN）；aij为负荷影响系数Aij的元素；yj为第j 个轴承的变位值（mm）；i， j 都分别表示1、2、3。

注:1、2、3 号轴承分别代表了后艉轴承、前艉轴承和推力轴承。

根据该轴系的相关设计要求，各轴承上负荷（kN）允许范围如表2 所示。

在轴系静态下进行校中优化， 不考虑轴承润滑油膜支撑刚度， 将该轴系校中优化问题简化为在约束范围内的线性规划下的最优化问题。 以后艉轴承上载荷最小为目标，校中优化后其他各轴承的状态参数在合理范围内且各轴承在竖直方向上的变位范围为（-10 mm，10 mm），得到该轴系合理校中结果如表3 所示。

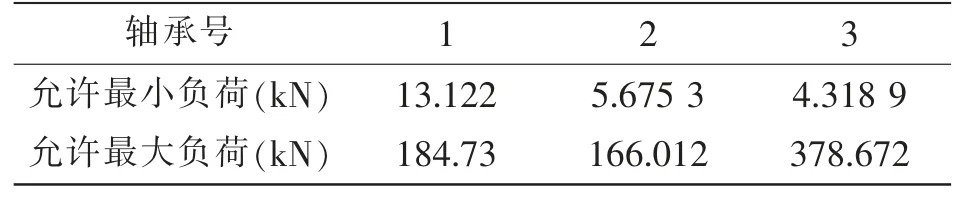
表2 各轴承上负荷允许范围Tab.2 Allowable range of load on each bearing

表3 合理校中各轴承状态Tab.3 Conditions of each bearing under reasonable alignment

通过比较表1 和表3 可知， 该轴系试验平台经过合理校中之后， 后艉轴承上的载荷减小了6.06 kN，前艉轴承上的载荷增加了17.74 kN，前后艉轴承上的载荷相差不大，可有效减小后艉轴承的异常磨损，轴系校中状态得到优化。

3 轴系试验平台振动计算

轴系在运转过程中的振动及由此产生的舰船船体声辐射， 是制约舰船声隐身性能的重要因素之一。 而轴系校中状态的改变会引起各轴承支撑载荷发生变化，轴系的弯曲状态和内部应力也会随之发生改变。 因此，研究计算轴系振动特性对其减振降噪具有重要意义。

3.1 轴承支撑油膜特性分析

轴承支撑油膜的厚度和动力学特性随着轴承位置和轴系转速的变化而变化。 因此，研究轴系不同校中和转速状态下油膜支撑特性[14]对轴系振动特性的影响十分重要。

基于滑动轴承动压润滑理论[10]，文中采用雷诺方程计算轴系试验平台在不同校中状态下各轴承支撑油膜压力分布。为了简化计算，假设其以30%的额定工况运行，且在运行过程中轴承温度不变，油膜为层流，不计惯性力的影响。

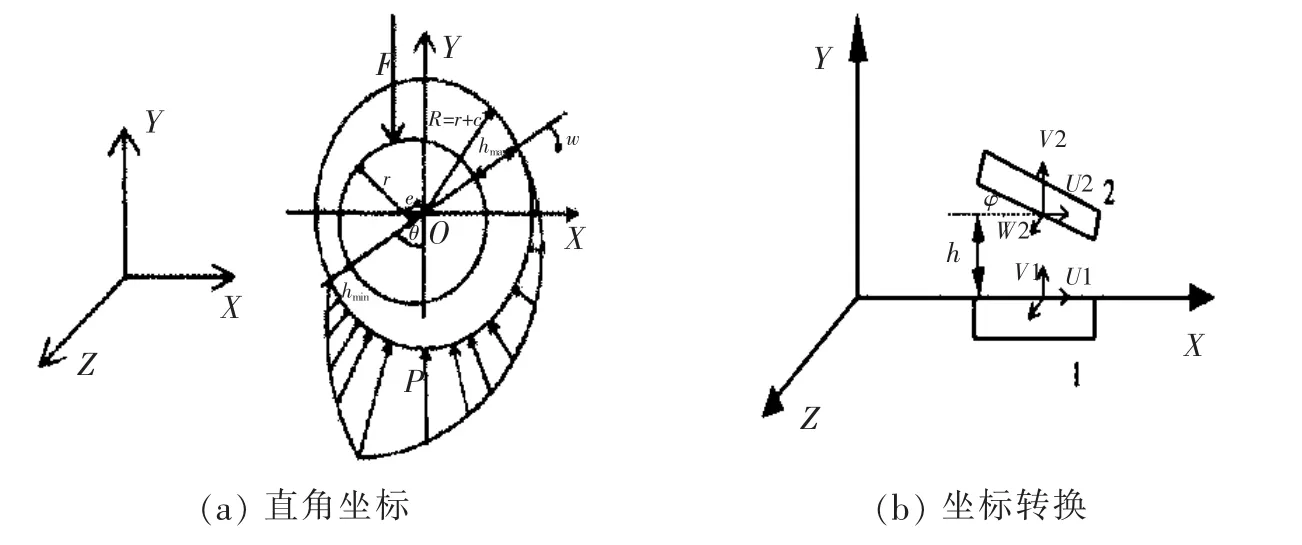
图7 轴承支撑油膜压力分布模型Fig.7 Pressure distribution model of support oil film on bearing

图7 为轴承支撑油膜压力分布模型在直角坐标系中示意图及坐标转换示意图。 通过轴承承载分析表明[13]:轴系运行过程中，受到载荷F 的作用，轴颈中心O2与轴承中心O1之间有一个偏心距离，它们的偏心距为e，偏心角为θ；轴承与轴颈间圆心距O1O2向两端的延长线与轴承和轴颈相交，两交线线段分别表示轴承和轴颈之间的最大间隙hmax=c+e 和最小间隙hmin=c-e， 其中c 为轴瓦与轴颈之间的半径间隙，r+c 为轴承孔内径，r 为轴颈半径；沿轴系旋转的方向ω，轴承和轴颈之间的间隙由hmax至hmin，是一个收敛的楔形，在这段间隙变化区间，油膜承受的压力是先逐渐增大后急剧减小。

对支撑油膜作如下假设:（1） 油膜在与轴颈和轴瓦接触面上无滑移；（2） 油膜体积不可压缩；（3）忽略油膜温度和粘度的变化。 建立各轴承支撑油膜运动雷诺方程:

由直角坐标系转换到圆柱坐标系可得

式中:r 为径向坐标（mm）；μ 为油膜的动粘度系数（Pa·s）；p 为油膜压力分布（Pa）；h 为油膜厚度（mm）；θ 为轴向坐标（rad）；ω 为轴系转速（rad/s）。

对（8）式进行无量纲化得

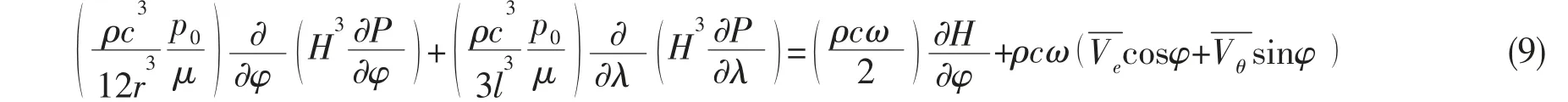
将坐标原点设在油膜厚度最大处（h=hmax），无量纲参数:φ=x/r；λ=2z/L 为轴颈的径向坐标z 与二分之一轴承轴向长度L 的比值；H=h/c 为油膜厚度与轴瓦轴颈间隙的比值。

对轴承支撑油膜压力分布积分，得支反力在圆柱坐标下的表达式为

式中:e 和θ 为轴承截面的偏心距和偏位角。

由（7）～（10）式就可根据各轴承上的载荷、轴系试验平台在不同校中状态下的轴承轴颈间的偏心距和偏位角，求得稳定工况下各轴承支撑油膜压力分布。

3.2 轴承支撑油膜刚度计算

轴系在运行过程中，将轴颈中心的变化简化为准静态过程，当轴承偏心距和偏位角发生变化时，采用小扰动法对其进行分析计算。

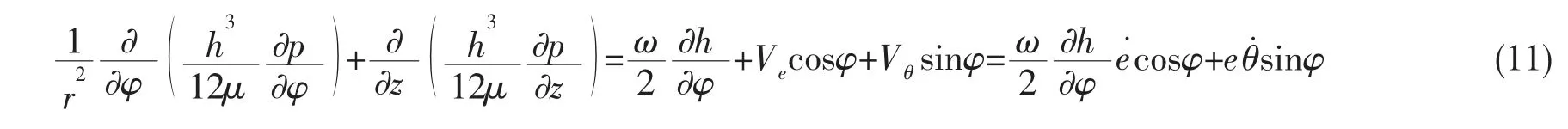
（11）式结合图7 可知，轴承支撑油膜压力分布与轴颈中心瞬时坐标（e，θ）及坐标变化速度（Ve，Vθ）有关，故轴承支撑油膜动态压力表达式为

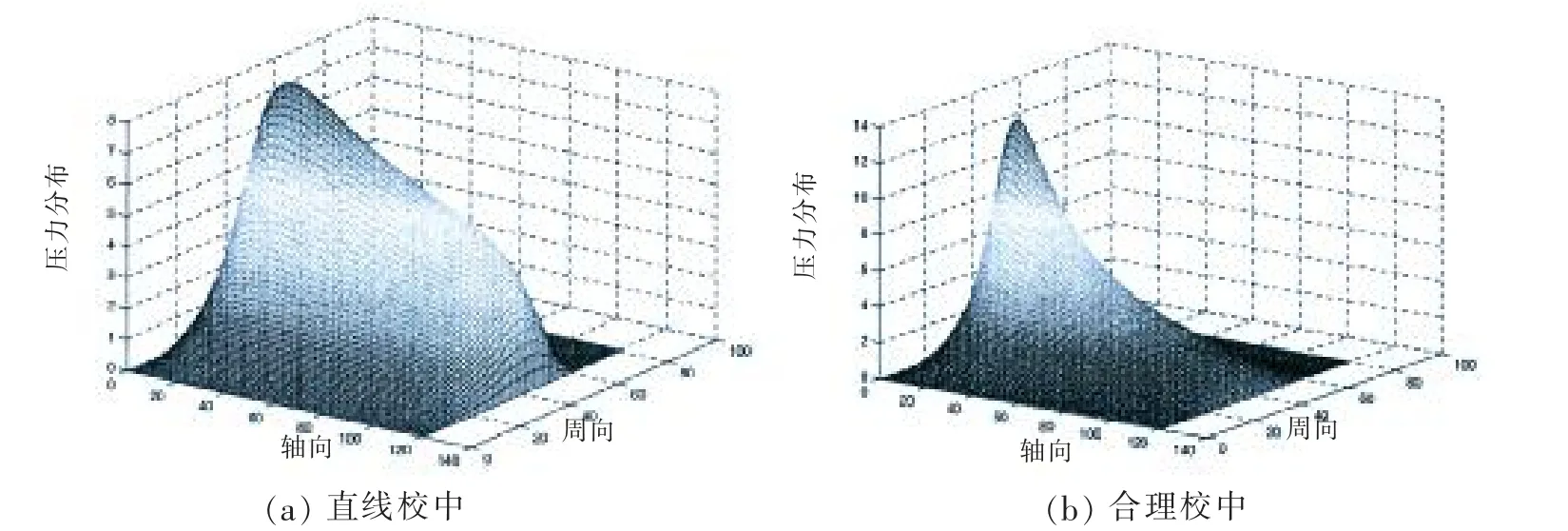
图8 不同校中状态下后艉轴承上油膜压力分布Fig.8 Pressure distribution of oil film on the aft stern bearing under different shafting alignment conditions

图8 显示了该轴系试验平台在直线校中和合理校中状态下，20%额定工况的后艉轴承上支撑油膜压力分布情况。

由图8 和轴系试验平台合理校中结果可知，经过合理校中，后艉轴承上的载荷较直线校中小，但靠近螺旋桨端油膜压力最大值增大。 同理可得其他两个轴承上油膜压力分布情况，在此不再赘述。

根据偏心距和偏位角的变化引起支撑油膜厚度的变化及刚度定义，可据下式求得油膜刚度:

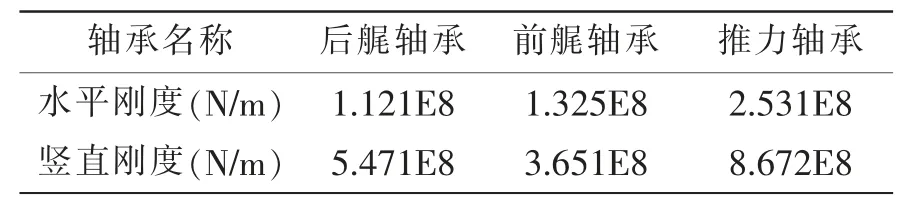
表4 各轴承支撑油膜刚度Tab.4 Stiffness of support oil film on each bearing

式中:e0和φ0为轴心初始稳态坐标。

得到轴系试验平台在直线校中状态下各轴承支撑油膜刚度如表4 所示。

采用相同方法可以计算求得该轴系试验平台在不同校中状态下各轴承支撑油膜刚度。

3.3 轴系试验平台模态分析

舰船在航行过程中，螺旋桨在水中产生的推力通过轴系以轴承力的形式传递至船体，从而推动船体运动。 由于螺旋桨产生的推力不是恒力而是随时间变化而变化的激振力，而轴系的固有属性对该激振力传递的放大和缩小有重要影响，因此可以根据2.1 节建立的轴系有限元模型对其进行模态分析。

图9 Combin214 支撑单元模型Fig.9 The mode of support element Combin214

轴系中各轴承的支撑作用采用Combin214 单元模拟， 推力轴承承受轴向推力作用采用弹簧单元模拟，该弹簧单元[13]的轴向刚度取为推力轴承推力块油膜刚度Koil， 轴系的纵向整体刚度Kz为推力轴承推力块油膜刚度与轴系结构刚度Kstr的串联值；Kyz、Kzy、Cyz和Czy分别代表了耦合刚度和耦合阻尼。 Combin214 单元如图9 所示。

文献[11]中研究了轴系推力块油膜刚度的计算方法，由该方法结合（16）式可得到该轴系的整体纵向刚度Kz。 图7 中Kyy和Kzz分别代表了该支撑轴承的竖直方向和水平方向的刚度（参考轴系纵向刚度计算方法求得）；Cyy和Czz分别代表了该支撑轴承的竖直方向和水平方向的阻尼（此处取值为厂家提供值）。

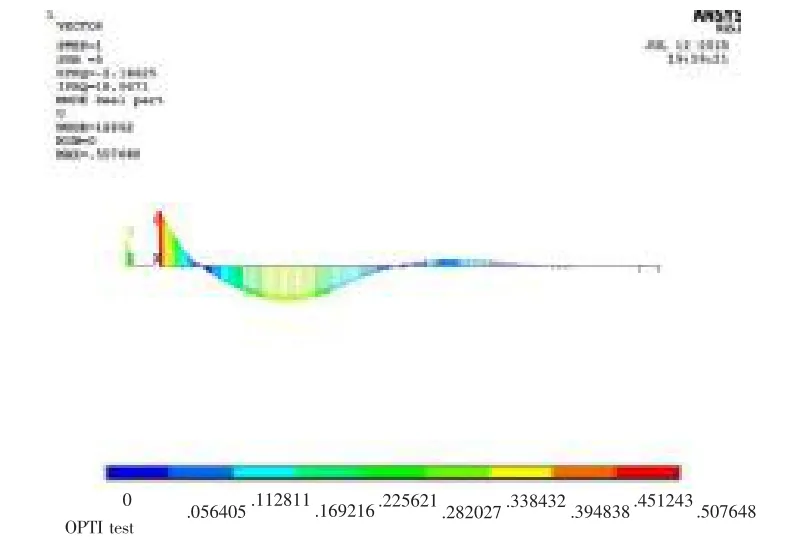
图10 水平方向一阶回旋振动振型图Fig.10 First order whirling vibration modal shape in the horizontal direction

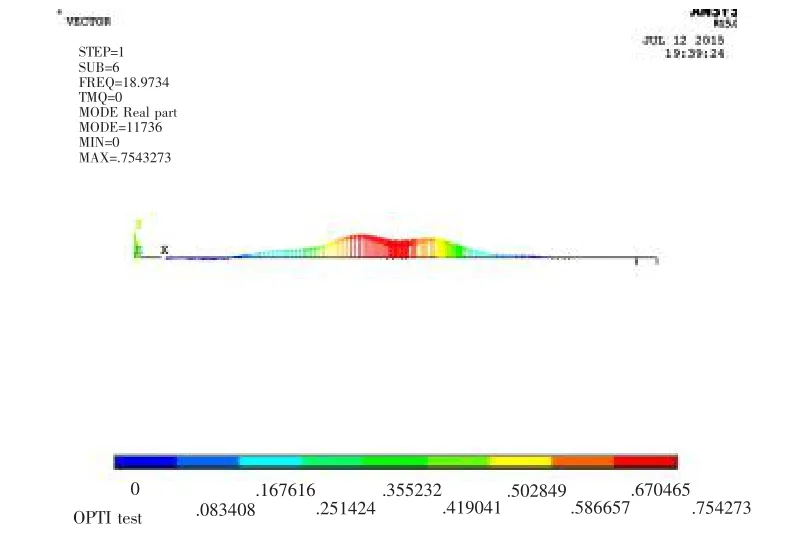
图11 竖直方向一阶回旋振动振型Fig.11 First order whirling vibration modal shape in the vertical direction

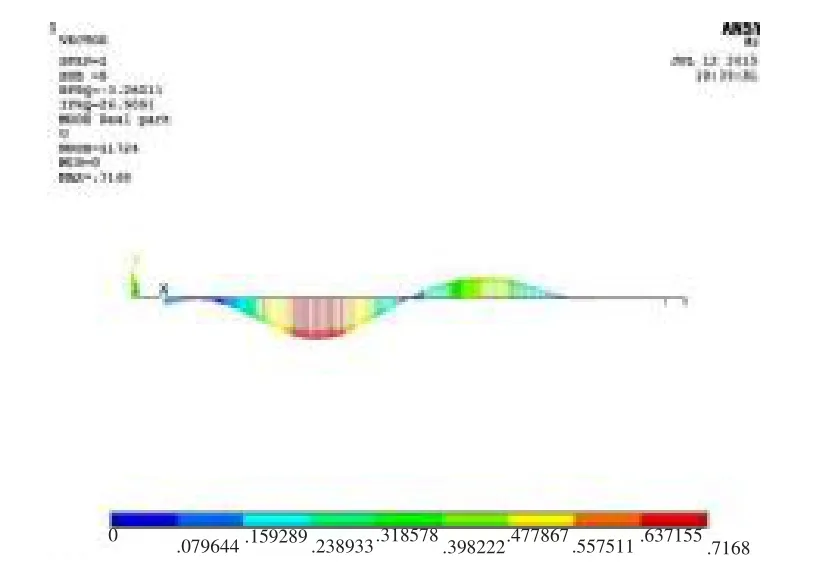
图12 水平方向二阶回旋振动振型图Fig.12 Second order whirling vibration modal shape in the horizontal direction

图13 竖直方向二阶回旋振动振型Fig.13 Second order whirling vibration modal shape in the vertical direction

由于轴系校中状态的变化对各轴承的支撑状态影响较大，而对轴系整体的纵向刚度的影响较小，因此，现着重研究轴系校中与轴系回旋振动的综合优化。 该轴系试验平台回旋振动模态计算主要是在弹性边界下的基本模态，直线校中状态下前两阶回旋振动模态如图10～13 所示。

由图10～13 可知，该轴系试验平台前两阶水平方向固有频率为18.06 Hz 和26.91 Hz，竖直方向固有频率为18.97 Hz 和27.06 Hz；横向激振力对推力轴承与螺旋桨之间的轴段影响最大，对推力轴承与高弹联轴器之间轴段影响较小。 因此，可在轴系试验平台的推力轴承与螺旋桨之间取两个节点作为参考，分析其振动特性以判定该轴系的回旋振动情况。

3.4 轴系试验平台回旋振动计算

根据3.2 节计算求得的各轴承水平和竖直方向刚度，建立刚度矩阵，根据有限元理论[15]，将轴系离散化为有限个小单元，单元与单元之间通过节点联系起来，单元与单元之间的位移、力和力矩通过节点传递，得其振动方程式:

式中:［M ］、［C ］和［K ］分别代表节点的质量矩阵、阻尼矩阵和刚度矩阵； ｛x¨｝、 ｛x˙｝和｛x ｝分别代表节点的加速度矩阵、速度矩阵和位移矩阵；｛F ｝为轴系节点所受的激振力向量。

为研究轴系试验平台的回旋振动频率响应情况，根据3.3 节中模态结果—螺旋桨与推力轴承之间轴段的振幅大于其他轴段， 可在螺旋桨与推力轴承之间取两个振动幅值较大的节点（节点33、 节点207）作为参考点，计算它们在0～200 Hz 范围内的回旋振动频率响应。

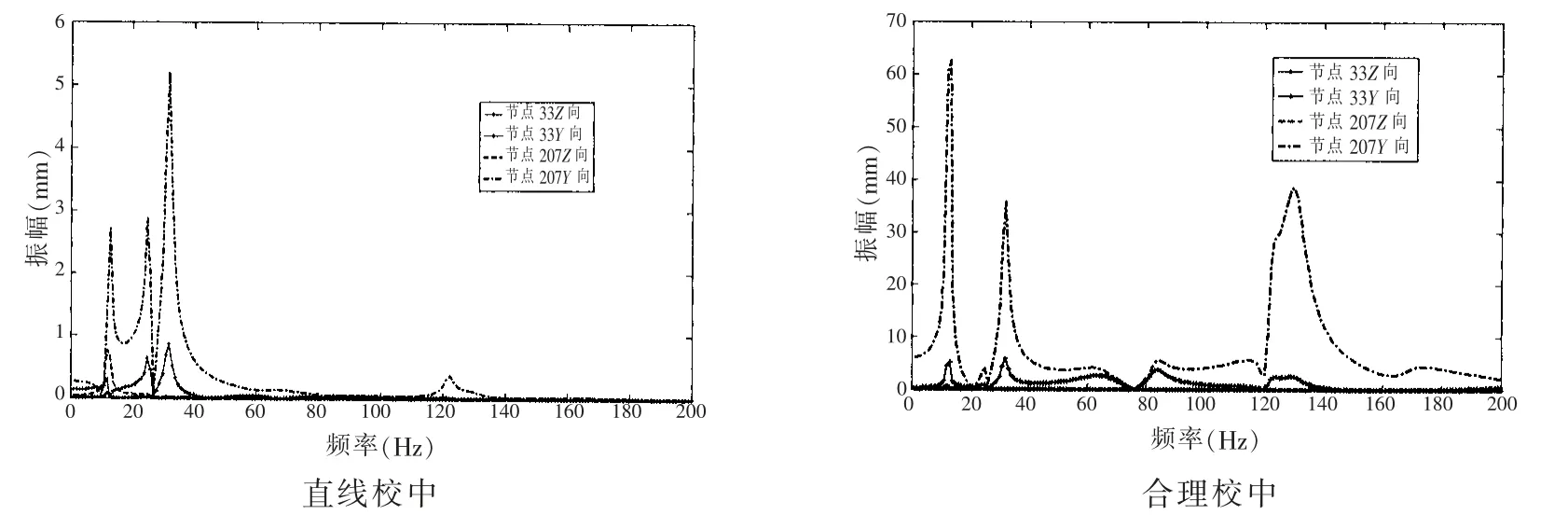
图14 不同校中状态下两参考点回旋振动频率响应Fig.14 Whirling vibration frequency response of two reference points under different alignment states

图14 给出了该轴系试验平台在直线校中和合理校中状态下节点33 和节点207 的水平方向和竖直方向上频率响应情况。

由图14 可知，该轴系试验平台经合理校中之后，轴系各轴承竖直方向位置改变引起轴系在竖直方向上的振幅变大程度远大于水平方向；节点207 的前四阶回旋振动Y 向共振频率有所增加，且第四阶共振幅值增加程度远大于前三阶共振；节点33 的前四阶回旋振动Y 向共振频率变化很小，振幅也有所增加；两节点的Z 向振动特性变化很小，因为调整各轴承的竖直方向的位置对轴承支撑油膜水平方向的刚度影响较小。

4 校中与减振综合优化

由2.4 节和3.4 节的结论可知，经轴系合理校中后，该轴系试验平台的校中质量得到较大的改善，即后艉轴承上的载荷明显减小。 这有利于减缓后艉轴承上的异常磨损， 但是其回旋振动特性有所恶化，因此，急需采取一定方法寻得最适合的轴系校中状态综合优化其校中状态和回旋振动特性。

4.1 综合寻优模型的建立

轴承变位直接影响轴承支撑油膜厚度和压力分布，但它对轴系回旋振动的影响不是线性的。 为了简化计算过程， 现只考虑调整后艉轴承在竖直方向的变位以同时优化轴系的校中状态和回旋振动特性，在直线校中的基础上，以步长为1 mm 分别计算在每一变位情况下后艉轴承的受载荷情况以及节点33 和节点207 处的回旋振动情况。

该优化目标优化函数可用以下数学表达式表示:

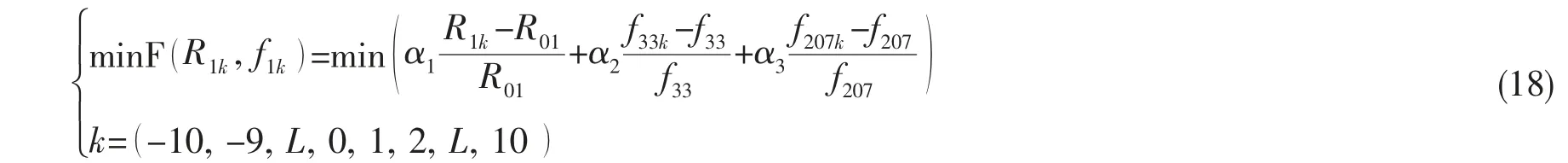
式中:α1、α2和α3分别代表后艉轴承上载荷减小程度、节点33 和节点207 回旋振动减振程度的权重系数； f33和f207分别代表直线校中状态下节点33 和节点207 回旋振动Y 向的最大振幅值；k 为后艉轴承调整变位值（mm）；R1k、 f33m和f207m分别代表后艉轴承调整k（mm）后，后艉轴承上载荷、节点33 和节点207 回旋振动Y 向的最大振幅值。

4.2 寻优计算

（18）式中的权重系数需根据轴系的实际情况确定，例如后艉轴承的异常磨损程度，前、后艉轴承上负荷差的大小，舰艇对轴系振动的要求等。

经2.3 节轴系校中计算可知，该轴系试验平台在直线校中状态下，Y 向振动最小，并且为确保各轴承载荷在合理范围内，后艉轴承的Y 向变位范围为（-5, 5）。 因此，只需计算比较后艉轴承变位为-1 mm、-2 mm、-3 mm、-4 mm、-5 mm 状态下和直线校中状态下节点33 和节点207 处的Y 向振动幅频特性。

图15 显示了该轴系试验平台在不同校中状态下两参考点处的Y 向振动幅频特性曲线。

由图15 可知，随着后艉轴承变位的增加， 该轴系试验平台在节点33 和节点207处的振幅峰值逐渐增大； 两参考点前四阶的共振频率很相近。

根据查阅相关资料并结合专家意见，确定权重系数α1、α2和α3分别为0.6、0.2 和0.2，代入（18）式计算得:当k=-2 mm 时，目标函数F （R1k, f1k）取得最小值。

图15 不同校中状态两参考点Y 向振动幅频特性Fig.15 Frequency response characteristics in Y direction of two reference points under different alignment states

5 结 论

在某电机驱动轴系试验平台直线校中的基础上， 本文根据滑动轴承润滑理论和转子动力采用有限元方法，计算了各轴承支撑油膜刚度和不同校中状态下该轴系试验平台的回旋振动幅频特性。 为简化计算，建立某一寻优模型只调整轴系后艉轴承的Y 向变位，得到k=-2 mm 时目标函数的值最小。 据此可知，当后艉轴承位置沿竖直方向向下移2 mm 时，该轴系试验平台状态最佳。 此时，后艉轴承上的载荷得到减小，可有效改善它的异常磨损，但轴系竖直方向的振动特性在一定程度上得到了恶化。 该方法的研究为轴系在校中设计阶段控制其振动特性提供了一个新思路， 具有较好的理论和工程实践价值。