考虑致密储层岩石特征参数的压敏效应计算新模型

2019-11-08殷代印孙业恒

特种油气藏 2019年5期

殷代印，刘凯，孙业恒

(1. 东北石油大学，黑龙江大庆 163318；2. 提高油气采收率教育部重点实验室,黑龙江大庆 163318； 3. 中国石化胜利油田分公司，山东东营 257000)

0 引言

近年来，合理有效地开发致密油藏成为行业研究的热点，准确地评价压敏效应是指导致密油藏开发的基础。目前，前人对致密储层压敏效应的研究大多只是针对某一渗透率级别，而未区分沉积岩类型[1-2]。窦宏恩等人应用实验方法研究了致密油藏压敏效应[3-5]；尹尚先、Jones等人基于实验结果，提出了不同形式的渗透率与有效应力经验模型[6-8]；曹耐等人基于Hertz接触变形理论，考虑渗透率初值和平均颗粒半径建立了致密储层应力敏感定量模型[9-10]；王厉强等人采用不等径迂曲毛管数模型、结合弹性厚壁桶理论定量地分析了压敏效应[11]；李玉丹等人基于岩心堆积模型分形理论和材料力学原理，考虑岩石杨氏模量和泊松比建立了压敏模型[12]。因此，不同沉积岩压敏模型需要同时考虑岩石特性参数和渗透率初值的影响。通过开展不同类型沉积岩压敏实验并进行压敏效应分析，依据实验结果，分别研究渗透率与有效应力的关系，有效应力敏感系数与岩石特性参数、渗透率初值的关系，进而建立适用于不同地区致密储层的压敏模型。

1 岩心压敏实验

1.1 渗透率测试原理

致密储层渗透率测试方法通常使用气体测试，这是由于渗透介质不与岩石固体骨架发生化学作用，同时气体渗流速度快，实验时间较短，避免了长时间实验引起的泄露、温度变化等带来的测量误差[13]。目前常用的气测渗透率方法主要有准静态法、气体压力脉冲法、气体流量法和脉冲衰减法等[14-15]。该研究所用实验仪器为法国Vinci公司制造的Coreval 700型覆压孔渗仪，其原理是脉冲衰减法测试渗透率，通过记录脉冲压力随时间的变化，计算岩样的气测渗透率。该仪器考虑了气体滑脱效应对渗透率测量结果的影响。

1.2 实验结果

室内实验主要通过设置不同的围压来模拟实际开发过程中有效应力的改变[16]。致密油藏埋深通常为2 200～4 000 m，有效应力压力梯度为0.013 1 MPa/m[17-18]，为模拟实际地层环境，设置围压变化范围为24 ～51 MPa。

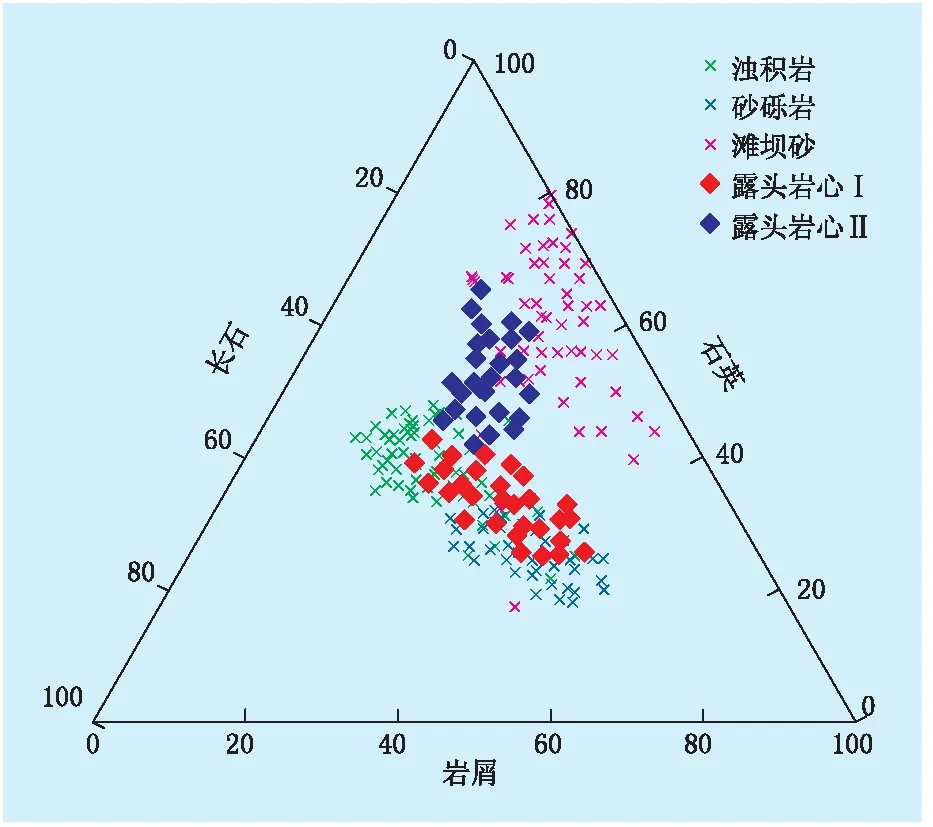
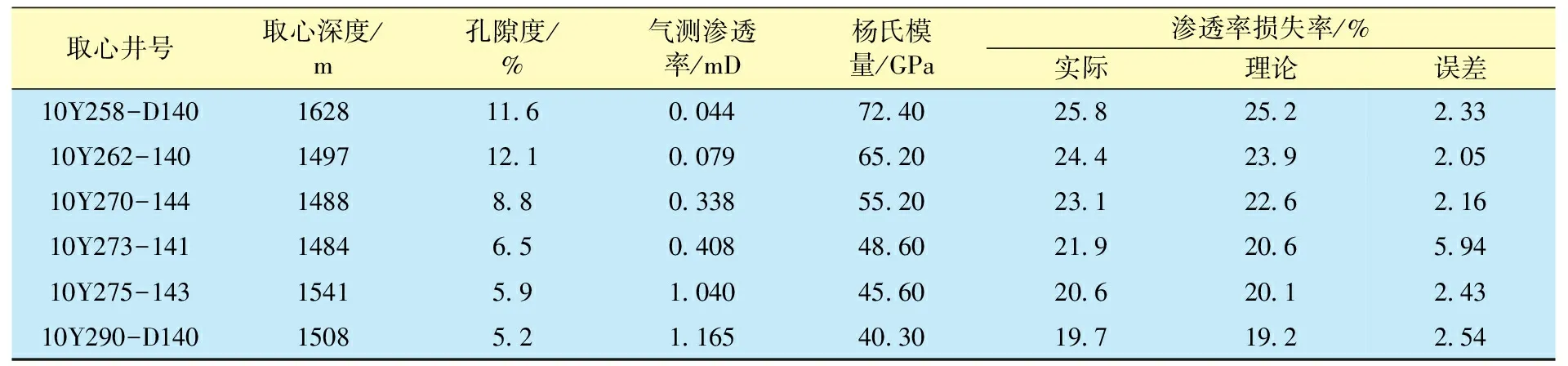
将各类沉积岩划分为5个渗透率(K，mD)级别(K≤ 0.1 , 0.1

表1 压敏实验岩心参数

图1 渗透率小于0.1 mD时不同沉积岩的应力敏感性

图2 不同渗透率下沉积岩的应力敏感性

由图1可知，不同类型沉积岩的应力敏感性也不同，砂砾岩最强，浊积岩居中，滩坝砂最弱，有效应力达51 MPa时，渗透率损失率分别为34.3%、30.6%和22.8%。由图2可知，同一沉积岩类型下，渗透率越低，应力敏感性越强，浊积岩渗透率为1.0～3.0 mD 和小于0.1 mD时，平均渗透率损失率分别为26.1%和30.6%。综合分析可知，区块整体应力敏感性表现为中等偏弱。

1.3 压敏效应分析

不同沉积岩压敏差异的主要原因是粒度组成、岩石成分、硬度和抗压能力不同，因此，从岩石粒度组成、成分和杨氏模量等方面，对不同类型沉积岩应力敏感差异进行了分析。表2为不同沉积岩基本参数，图3为岩石成分三角分布。分析不同沉积岩的粒度组成可知，滩坝砂主要由碳酸盐质砂岩和粉砂岩组成，大颗粒间孔隙由粉砂岩和泥质砂岩填充，压实后抗压能力强，应力不敏感；砂砾岩主要为砾质砂岩和砂岩，分选性较好，固体颗粒粒级相对较大，可动孔隙较大。分析不同沉积岩的成分可知，滩坝砂中石英含量高达68.90%，岩石硬度大，抗压能力强；浊积岩中石英和长石含量相当，岩屑含量较少，抗压能力相对较弱；砂砾岩中石英和岩屑含量较多，欠成熟直接压实形成，当有效应力增加时，固体颗粒重新排列，导致孔隙喉道收缩甚至闭合，应力敏感性较强。分析不同沉积岩的杨氏模量可知，岩石的杨氏模量越大，可压缩性越低，多孔介质变形程度越小，应力越不敏感。滩坝砂的平均杨氏模量最大，为133.65 GPa；砂砾岩的平均杨氏模量最小，为91.84 GPa。

表2 不同沉积岩类型参数

图3 各类岩石成分三角分布

2 广义压敏模型

2.1 压敏模型的建立

依据压敏实验结果，渗透率与有效应力呈指数变化关系。通过拟合实验数据，建立了有效应力敏感系数与杨氏模量和渗透率初值的经验公式：

Km=Kmoe-(c1αE+c2αKmo)σ

(1)

式中：Km为不同有效应力下的渗透率，mD；Kmo为初始渗透率，mD；c1,c2分别为杨氏模量和渗透率初值对有效应力敏感系数的贡献率；αE,αKmo分别为有效应力敏感系数与杨氏模量、有效应力敏感系数与渗透率初值的关系，MPa-1；σ为有效应力，MPa。

分别统计有效应力敏感系数与杨氏模量和渗透率初值的关系。图4为不同渗透率级别下敏感系数与杨氏模量的关系，对不同渗透率级别的样本点分别拟合后取平均值，则有效应力敏感系数与杨氏模量呈对数关系。

αE=1.465-0.3553lnE

(2)

式中：E为杨氏模量，GPa。

图4 应力敏感系数与杨氏模量分布关系

图5为不同杨氏模量下应力敏感系数与渗透率初值的关系，对不同岩性样本点分别拟合后取平均值，则有效应力敏感系数与渗透率初值呈幂函数关系。

(3)

图5 应力敏感系数与渗透率初值分布关系

利用式(2)和式(3)，可以将有效应力敏感系数与杨氏模量和渗透率初值的非线性关系转换为线性关系。应用多元线性回归模型[19-20]，确定了有效应力敏感系数为：

α=1.1035αE-0.1366αKmo

(4)

式中：α为有效应力敏感系数。

将式(4)代入式(1)，得到考虑岩石特性参数的压敏新模型：

Km=Kmoe-(1.1035αE-0.1366αKmo)

(5)

2.2 模型验证

该压敏模型由大量的天然气岩心压敏实验数据回归得出，可信度高，适用性强。为了推广至其他致密储层，在3种岩性基础上补充了2种露头岩心，拓宽了岩石参数范围，并且将杨氏模量和渗透率初值作为参数引入压敏模型，能够适用于不同地区致密储层。为了验证其准确性，取大庆长垣外围树9-2区块致密储层6块不同渗透率级别的天然岩心，进行压敏实验，岩心基本参数及模型验证结果见表3。由表3可知，平均渗透率损失率计算误差为2.91%。结果表明，压敏新模型适用于其他地区致密储层，计算结果可靠。

3 实例应用

对于不同地区的致密储层，仅需已知岩石的杨氏模量，应用压敏模型即可计算出渗透率随有效应力的变化，而不需要进行压敏实验。将压敏新模型引入到致密储层非达西渗流方程，可以推导出适用于不同地区致密储层考虑压敏效应的产能计算公式。

表3 岩心基本参数及模型验证结果

将式(5)引入致密储层非达西渗流方程，则有：

(6)

式中：vm为渗流速度，m/s；μo为原油黏度，MPa·s；G为启动压力梯度，MPa/m。

将式(6)进行积分，结合式(5)，并参照文献[21]，得到考虑压敏效应的直井垂直裂缝产能预测公式：

(7)

式中：xf为裂缝半长，m；h为油层厚度，m；Bo为原油体积系数；β为上覆岩压应力梯度，MPa/m；H为油藏埋深，m；pe为供给压力，MPa；pw为井底流压，MPa；re为泄油半径，m；wf为缝宽，m。

以济阳坳陷盐家油田砂砾岩致密储层为例，盐22-23井裂缝半长为89 m，初始平均渗透率为0.892 mD，岩石杨氏模量为94.80 GPa，导流能力为32 D·cm，油层厚度为12.7 m，地下原油黏度为1.5 MPa·s，上覆岩石压应力梯度为0.023 2 MPa/m，油藏中部埋深为3 426 m，启动压力梯度为0.1720 MPa/m。该井投产后，地层压力和井底流压的变化见图6。应用不考虑压敏效应的产能公式、考虑压敏效应但不考虑杨氏模量影响的产能公式和引入压敏新模型建立的产能公式分别计算相应生产压差下的理论日产液量，并与实际日产液量对比(图6)。由图6可知，盐22-23井投产后，地层能量没有得到及时补充，地层压力和井底流压不断下降，井底流压在2010年1月之后基本不变，生产压差不断减小。不考虑压敏效应的产能下降幅度与生产压差下降幅度基本一致，但与实际相比偏差很大，日产液量预测平均误差为39.10%；考虑压敏效应但不考虑岩石杨氏模量影响的产能预测结果仍与实际产量有一定偏差，误差为18.20%，这是由于不同地区致密储层应力敏感性存在差异；应用压敏效应新模型建立的产能公式考虑了岩石特性参数的影响，产能预测结果与实际相比吻合度较高，误差为4.98%。