高考中线性规划常见题型及解法

河南省新密市第二高级中学 申伟洲

线性规划问题是高考的重点，它是数形结合思想的载体。线性规划问题具有代数和几何的双重形式，多与函数、平面向量、数列、三角、概率、解析几何等问题交叉渗透，自然地融合在一起，使数学问题的解答变得更加新颖别致。

归纳起来常见的命题探究角度有：

1.求线性目标函数的最值；

2.求非线性目标函数的最值；

3.求线性规划中的参数；

4.线性规划的实际应用。

下面主要讲解线性规划的常见基础类题型。

一、求可行域的面积

例1不等式组表示的平面区域的面积为( )。

A.4 B.1

C.5 D.6

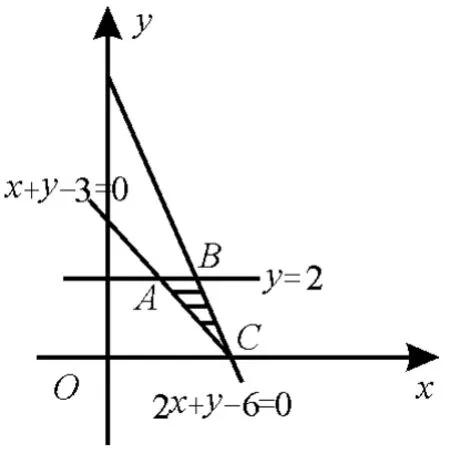
图1

解析：如图1，作出对应可行域，△ABC的面积即为所求，由梯形OMBC的面积减去梯形OMAC的面积即可，答案为B。

二、求可行域中整点个数

例2满足|x|+|y|≤2的点(x，y)中整点(横纵坐标都是整数)有( )。

A.9个 B.10个

C.13个 D.14个

解析：|x|+|y|≤2 等价于

作出可行域如图2，正方形内部(包括边界)，容易得到整点个数为13，选C。

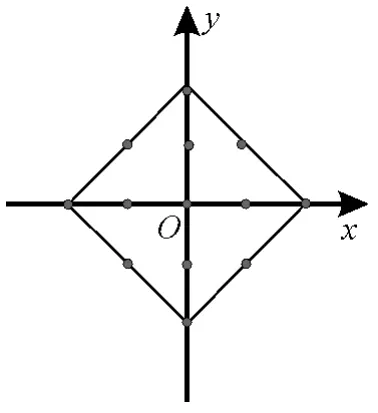
图2

三、求线性目标函数的取值范围

(一)“截距”型考题

在线性约束条件下，求形如z=ax+by(a，b∈R)的线性目标函数的最值问题，通常转化为求直线在y轴上的截距的取值。结合图形易知，目标函数的最值一般在可行域的顶点处取得。掌握此规律可以有效避免因画图太草而造成的视觉误差。

例 3若x，y满足约束条件则z=x+y的最大值为_____。

解析：由不等式组画出可行域，图3中阴影部分(含边界)。目标函数x+y取得最大值，即斜率为-1的直线x+y=z(z看作常数)在y轴上的截距最大，由图可知当直线x+y=z过点C时，z取得最大值。

故zmax=5+4=9。

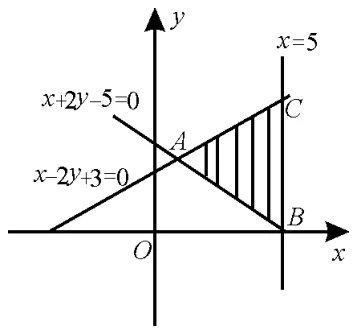
图3

例4若x，y满足约束条件则z=3x-4y的最小值为_____。

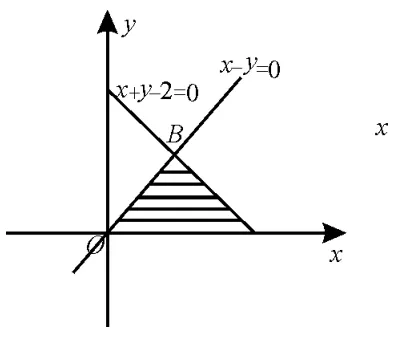
图4

解析：由z=3x-4y，得作出不等式对应的可行域(图4 中阴影部分)。平移直线由平移可知当直线经过点B(1，1)时，直线y=的截距最大，此时z取得最小值。

将B的坐标代入z=3x-4y，目标函数z=3x-4y的最小值为-1。

例5已知x，y∈R，且满足则z=|x+2y|的最大值为( )。

A.10 B.8 C.6 D.3

解析：作出不等式组对应的平面区域，如图5中的阴影部分。

由z=|x+2y|，平移直线，由图像可知当直线经过点A时，z取得最大值，此时z最大。即A(-2，-2)，代入目标函数z=|x+2y|得z=2×2+2=6。(此题也可利用点到直线的距离公式求解)

(二)“距离”型考题

在线性约束条件下，求形如z=(x-a)2+(y-b)2的线性目标函数的最值问题，通常转化为求点(a，b)到阴影部分的某个点的距离的平方的值。

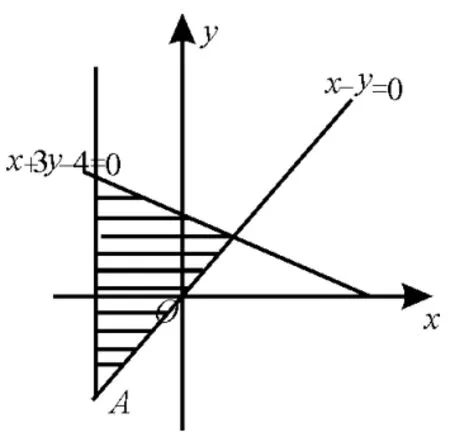
图5

例6(2016年山东卷)若变量x，y满足则x2+y2的最大值是( )。

A.4 B.9 C.10 D.12

解析：由约束条件作出可行域，如图6所示。

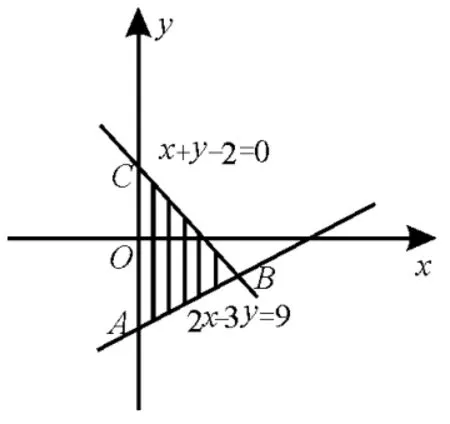
图6

因为A(0，-3)，C(0，2)，所以|OA|＞|OC|。

例 7如果实数x，y满足则z=x2+y2-2x的最小值是( )。

解析：z=x2+y2-2x=(x-1)2+y2-1。

设m=(x-1)2+y2，则m的几何意义是区域内的点到点D(1，0)的距离的平方，作出不等式组对应的平面区域，如图7所示。

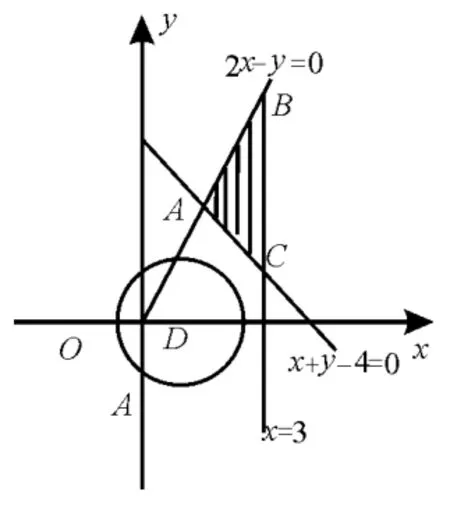
图7

由图像知D到AC的距离为最小值。

(三)“斜率”型考题

例8若x，y满足不等式组的最大值是( )。

图8

例 9已知变量x，y满足的取值范围是( )。

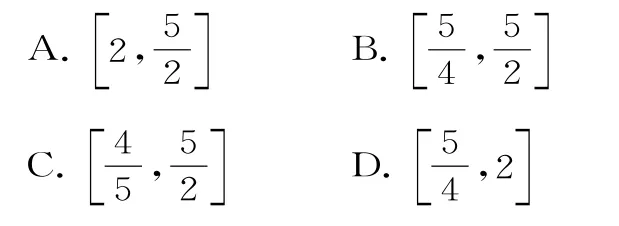
解析：作出满足所对应的区域(如图9中的阴影)。

由图像可知当直线经过点B(2，0)时，目标函数取最小值1+；当直线经过点C(0，2)时，目标函数取最大值选B。

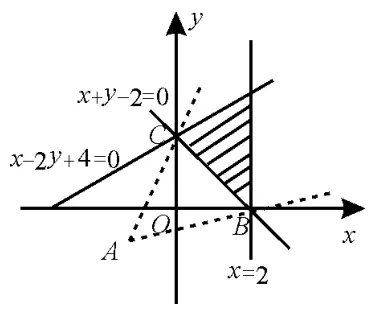
图9

总结：1.求目标函数最值的一般步骤为：一画，二移，三求。关键是准确作出可行域，理解目标函数的意义。

2.常见的目标函数有以下几种。

(1)截距型。形如z=ax+by。

求这类目标函数的最值时，常将函数z=ax+by转化为直线的斜截式，通过求直线的截距的最值，间接求出z的最值。

(2)距离型。情形一：如z=，此类目标函数常转化为点(x，y)与定点的距离；

情形二：z=(x-a)2+(y-b)2，z=x2+y2+Dx+Ey+F，此类目标函数常转化为点(x，y)与定点的距离的平方。

四、线性规划中的含参数问题

(一)“求约束条件中的参数”型考题

当参数在线性规划问题的约束条件中时，作可行域要注意应用“过定点的直线系”知识，使直线“初步稳定”，再结合题中的条件进行全方面分析，才能准确获得答案。

例10若不等式组所表示的平面区域被直线分为面积相等的两部分，则k的值是( )。

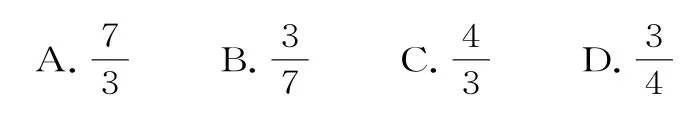
解析：不等式组表示的平面区域，如图10所示。

由于直线y=kx+过定点，因此只有直线过AB中点时，直线能平分平面区域。因为A(1，1)，B(0，4)，所以AB中点。当y=kx+过点，所以选A。

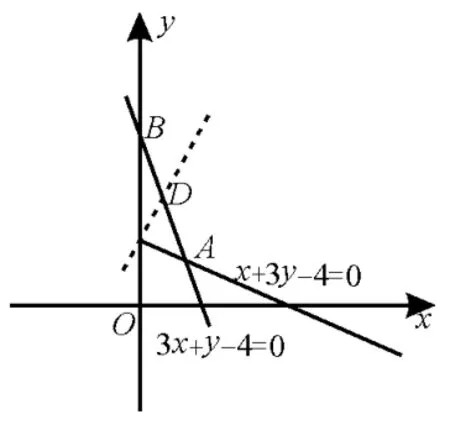
图10

例11若x，y满足不等式组的最大值为2，则实数m的值为( )。

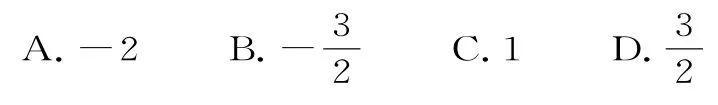
解析：因为的最大值为2，所以此时满足

作出不等式组对应的平面区域，如图11。

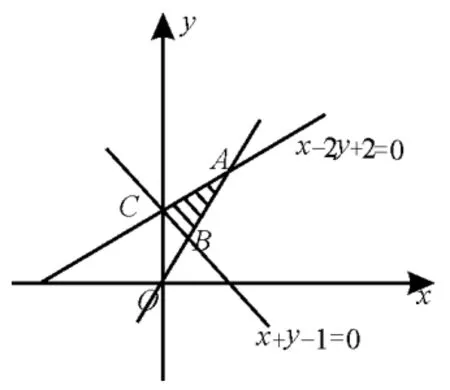
图11

同时A也在直线y=mx上，则选D。

例12(2014 年高考北京卷)若x，y满足且z=y-x的最小值为-4，则k的值为( )。

解析：作出线性约束条件的可行域。

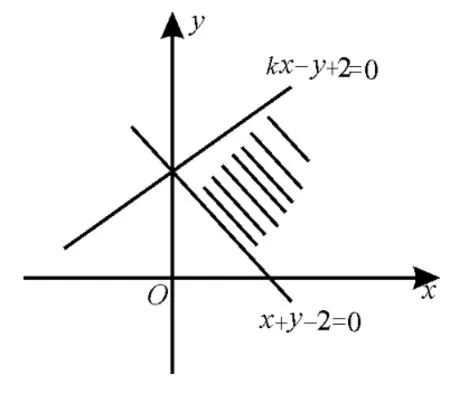
图12

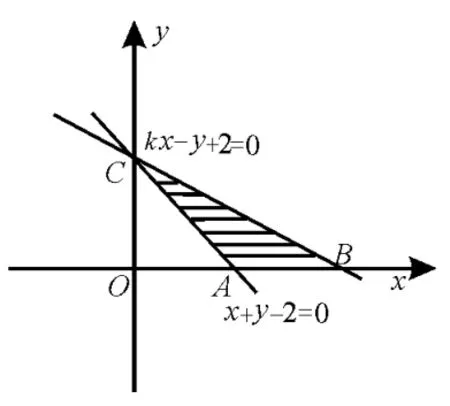
图13

当k＞0时，可行域如图12中阴影部分所示，显然此时z=y-x无最小值。

当k＜-1时，z=y-x取得最小值2；当k=-1时，z=y-x取得最小值-2，均不符合题意。

当-1＜k＜0时，可行域如图13中阴影部分所示，当直线z=y-x经过点时，有最小值，即，选D。

(二)“求目标函数中的参数”型考题

目标函数中含有参数时，要根据问题的意义，转化成“直线的斜率”、“点到直线的距离”等模型进行讨论与研究。

例13设x，y满足约束条件若目标函数z=ax+by(a＞0，b＞0)的最小值为2，则ab的最大值为( )。

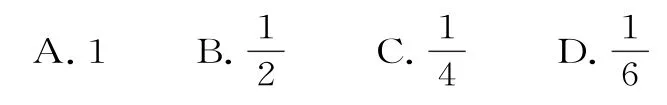
解析：满足约束条件的可行域，如图14所示。

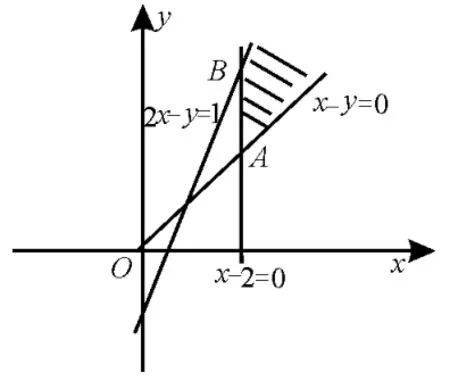
图14

因为目标函数z=ax+by(a＞0，b＞0)，故zA=2a+2b，zB=2a+3b。

目标函数z=ax+by(a＞0，b＞0)的最小值为2，则2a+2b=2，即a+b=1。则，ab的最大值为，选C。

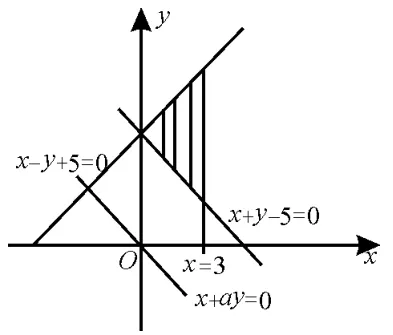
图15

例14已知x，y满足以下约束条件，使z=x+ay(a＞0)取得最小值的最优解有无数个，则a的值为( )。

A.-3 B.3 C.-1 D.1

解析：如图15，作出可行域，作直线l：x+ay=0，要使目标函数z=x+ay(a＞0)取得最小值的最优解有无数个，则将l向右上方平移后与直线x+y=5重合，故a=1，选D。

五、线性规划与其他问题结合

例15已知函数f(x)=-x2+ax-b，若a，b都是从区间[0，4]内任取的一个数，则f(1)＞0成立的概率是( )。

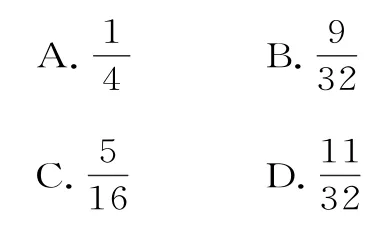
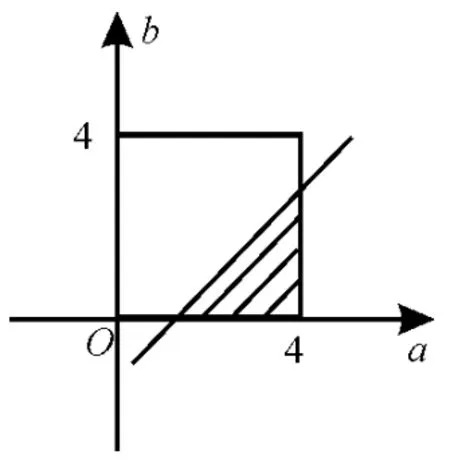
图16

解析：f(1)=-1+a-b，令f(1)＞0，则a-b＞1。又0≤a≤4，0≤b≤4，满足ab＞1的阴影部分，如图16所示。

例16(2016 年湖州质检)已知O为坐标原点，A，B两点的坐标均满足不等式组则tan∠AOB的最大值等于( )。

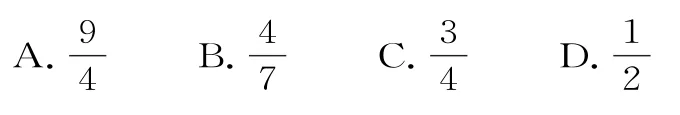
解析：如图17 所示，阴影部分为不等式组表示的平面区域。

观察图形可知当A为(1，2)，B为(2，1)时，tan∠AOB取得最大值，此时由于tanα=，故tan∠AOB=tan(β-α)=，选C。

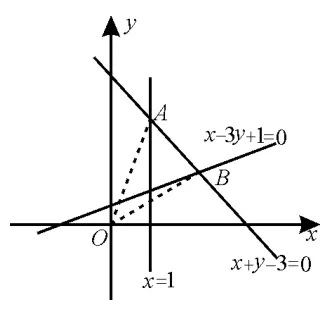
图17

六、实际问题

例17某高科技企业生产A产品和B产品需要甲、乙两种新型材料，生产一件A产品需要甲材料1.5 kg，乙材料1 kg，用5个工时；生产一件B产品需要甲材料0.5 kg，乙材料0.3 kg，用3个工时。生产一件A产品的利润为2 100 元，生产一件B产品的利润为900 元。该企业现有甲材料150 kg，乙材料90 kg，则在不超过600 个工时的条件下，求生产A产品、B产品的利润之和的最大值。

解析：A、B两种产品每件分别是x件和y件，获利为z元。

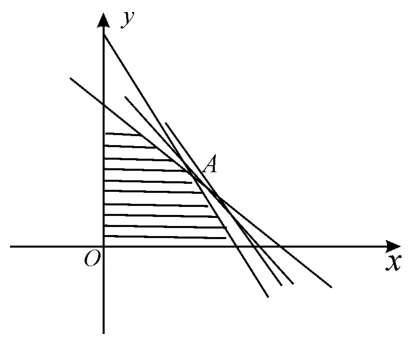
图18

目标函数z=2 100x+900y经过A时，直线的截距最大，利润之和的最大值为2 100×60+900×100=216 000(元)。