全国名校不等式测试题（A 卷）参考答案与提示

一、选择题

1.D 2.B 3.C 4.B 5.B 6.C 7.A 8.A 9.C 10.C 11.C 12.C 13.B 14.B 15.B 16.D 17.D 18.C 19.A 20.B 21.A 22.B 23.B 24.D 25.C 26.A 27.B 28.B 29.A 30.D 31.A 32.C 33.A 34.C 35.B 36.A 37.A 38.D 39.B

二、填空题

三、解答题

60.(1)由x＜-1或x≥1。

故A=(-∞，-1)∪[1，+∞)。

(2)由题意知(x-a-1)(2a-x)＞0，故(x-a-1)(x-2a)＜0。

因为a＜1，所以a+1＞2a，故B=(2a，a+1)。

因为B⊆A，所以2a≥1或a+1≤-1。解得或a≤-2。而a＜1，所以a＜1或a≤-2。

故当B⊆A时，实数a的取值范围是

61.设矩形温室的左侧边长为am，后侧边长为bm，则ab=800。

蔬菜的种植面积S=(a-4)(b-2)=ab-4b-2a+8=808-2(a+2b)。

当且仅当a=2b，即a=40，b=20 时，S最大值=648(m2)。

故当矩形温室的左侧边长为40 m，后侧边长为20 m 时，蔬菜的种植面积最大，最大种植面积为648 m2。

62.当a=0时，不等式的解集为{x|x＞1}。

当a≠0时，分解因式得1)＜0。

当a＜0时，原不等式等价于-1)＞0，不等式的解集为

当0＜a＜1 时不等式的解集为

当a=1时，不等式的解集为∅；

当a＞1 时，，不等式的解集为

63.(1)因为f(x)=ax2+a2x+2ba3，且当x∈(-2，6)时，f(x)＞0；当x∈(-∞，-2)∪(6，+∞)时，f(x)＜0，所以-2和6是方程ax2+a2x+2b-a3=0的两根。

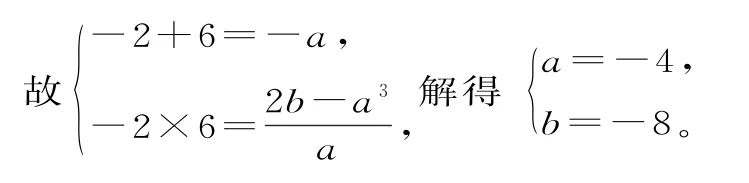
此时，f(x)=-4x2+16x+48。

(2)F(x)=4(k+1)x+2(6k-1)=kx2+4x-2。

欲使F(x)＜0恒成立，只要使kx2+4x-2＜0恒成立，则需要满足：

①当k=0时，原不等式化为4x-2＜0，显然不合题意，舍去；

②当k≠0时，要使二次不等式的解集为x∈R，则必须满足：

综合①②知，k的取值范围为(-∞，-2)。

64.设分别组装P、Q产品x件、y件，则：

设利润z=1 000x+2 000y=1 000(x+2y)。

要使利润最大，只需求z的最大值。

图1

作出可行域如1图示(阴影部分及边界)。

作出直线l：1 000(x+2y)=0，也即x+2y=0。

由于向上平移直线l时，z的值增大，所以在点A处z取得最大值。

因此，此时最大利润zmax=1 000(x+2y)=400(万元)。故要使月利润最大，需要分别组装P、Q产品2 000件、1 000件，此时最大利润为400万元。

65.(1)设矩形的另一边长为am，则y=45x+180(x-2)+180×2a=225x+360a-360。由已知xa=360，得

(2)因为x＞2，所以

修建围墙的总费用最少是10 440元。

66.(1)因为a2=x2+xy+y2，c2=x2+2xy+y2所以c2-a2=xy。

因为x＞0，y＞0，所以xy＞0，即c＞a。

(2)当p=1时，因为，所以c为最大边。

又(a+b)2=x2+2xy+y2+2ab＞x2+2xy+y2=c2，故a+b＞c，从而以a，b，c为三边长一定能构成三角形。

(3)因为a+b＞c，即，所以整理得：

67.要使函数f(x)=x2+ax+3，当x∈[-2，2]时，f(x)≥a恒成立，即函数f(x)=x2+ax+3在x∈[-2，2]上的最小值大于等于a。

68.(1)在△ADE中，y2=x2+AE2-2x·AE·cos 60°⇒y2=x2+AE2-x·AE。①

又由题意可求得1≤x≤2。

故y关于x的函数关系式是y=

(2)如果DE是水管，则，当且仅当时，等号成立，故

如果DE是参观线路，记函数f(x)=，可知该函数在上递减，在上递增，故f(x)max=max{f(1)，f(2)}=5。所以，此时x=1或x=2。故DE为AB边中线或AC边中线时，DE取得最大值，且最大值为

69.(1)若a=0，则b=-c。

f(0)·f(1)=c(3a+2b+c)=-c2≤0，与已知矛盾，所以a≠0。

方程3ax2+2bx+c=0 的判别式Δ=4(b2-3ac)。

由条件a+b+c=0，消去b，得Δ=

故方程f(x)=0有实根。

(2)因为f(0)＞0，f(1)＞0，所以c＞0，3a+2b+c＞0。

由条件a+b+c=0，消去b，得a＞c＞0。由条件a+b+c=0，消去c，得a+b＜0，2a+b＞0，故

(3)抛物线f(x)=3ax2+2bx+c的顶点坐标为的两边乘以

又因为f(0)＞0，f(1)＞0，而所以方程f(x)=0 在区间内分别有一实根。故方程f(x)=0在(0，1)内有两个实根。