四种条件的判断与应用

河南省平顶山一高 刘邓辉

一、利用定义判断

例1设x∈R，则是“x3＜1”的( )。

A.充分而不必要条件

B.必要而不充分条件

C.充要条件

D.既不充分也不必要条件

解析：由得0＜x＜1，则0＜x3＜1，即

由x3＜1，得x＜1，但 当x≤0 时，

点评：直接判断“若p，则q”、“若q，则p”的真假时，要确定条件是什么、结论是什么。

练习1：“a=0”是“函数f(x)=sinx-为奇函数”的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

解析：f(x)的定义域为{x|x≠0}，关于原点对称。当，故f(x)为奇函数。

二、利用集合间的关系进行判断

例2设p：实数x，y满足(x-1)2+(y-1)2≤2，q：实数x，y满足则p是q的( )。

A.必要不充分条件

B.充分不必要条件

C.充要条件

D.既不充分也不必要条件

解析：如图1，作出p，q表示的区域，其中☉M及其内部为p表示的区域，△ABC及其内部(阴影部分)为q表示的区域，故p是q的必要不充分条件。

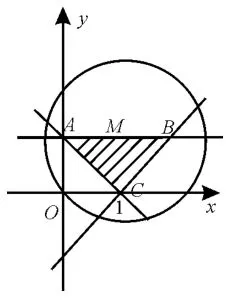
图1

点评：利用集合中的包含思想，抓住“以小推大”的技巧，即小范围推得大范围，即可解决充分必要性的问题。

练习2：已知m∈R，“函数y=2x+m-1有零点”是“函数y=logmx在(0，+∞)上是减函数”的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

解析：由y=2x+m-1=0，得m=1-2x，则m＜1，即A={m|m＜1}。

由于函数y=logmx在(0，+∞)上是减函数，故0＜m＜1，即B={m|0＜m＜1}。

因为B⊆A，所以“函数y=2x+m-1有零点”是“函数y=logmx在(0，+∞)上是减函数”的必要不充分条件。

三、利用互为逆否命题的等价性进行判断

由于互为逆否命题是相互等价的，当我们对原命题判断较为困难时，可将其转化为逆否命题来判断。

例3已 知p：|3x-4|＞2；q：，问：¬p是¬q的什么条件?

解析：由|3x-4|＞2，得x＞2或也即p：x＞2或，得x＞2或x＜-1，即q：x＞2或x＜-1。容易判断q是p的充分不必要条件，从而¬p是¬q的充分不必要条件。

点评：条件和结论带有否定性词语的命题，常转化为其逆否命题来判断真假。

练习3：p：x≠3且y≠2，q：x+y≠5，说明p是q的什么条件。

解析：原命题等价于判断¬q：x+y=5是¬p：x=3或y=2的什么条件。

显然¬q⇒/¬p，¬p⇒/¬q，所以p是q的既不充分也不必要条件。

四、充分条件、必要条件的探究

例4命题“∀x∈[1，3]，x2-a≤0”为真命题的一个充分不必要条件是( )。

A.a≥9 B.a≤9

C.a≥10 D.a≤10

解析：命题“∀x∈[1，3]，x2-a≤0”⇔“∀x∈[1，3]，x2≤a”，9≤a。则a≥10是命题“∀x∈[1，3]，x2-a≤0”为真命题的一个充分不必要条件。

点评：充分条件、必要条件的探究，关键是正确化简条件，寻求问题成立的充要条件。

练习4：圆x2+y2=1与直线y=kx-3有公共点的充分不必要条件是( )。

解析：若直线与圆有公共点，则圆心(0，0)到直线kx-y-3=0的距离≤1，即，k2+1≥9，k2≥8，k≥所以圆x2+y2=1 与直线y=kx-3有公共点的充分不必要条件是，选B。

五、充分条件、必要条件的应用

例5已知p：|2x-3|＜m，q：x(x-3)＜0，若p是q的充分不必要条件，则实数m的取值范围是____。

解析：设|2x-3|＜m和x(x-3)＜0的解集分别为A，B。易知B={x|0＜x＜3}，当m≤0时A=∅，符合题意；当m＞0时，A要使p是q的充分不必要条件，则AB，应有

综上，实数m的取值范围是m＜3。

点评：根据充分、必要条件求解参数范围的方法及注意点：

(1)把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解。

(2)要注意区间端点值的检验。尤其是利用两个集合之间的关系求解参数的取值范围时，不等式是否能够取等号决定端点值的取舍，处理不当容易出现漏解或增解的现象。

练习5：设p：实数x满足x2-4ax+3a2＜0，a∈R；q：实数x满足x2-x-6≤0 或x2+2x-8＞0。若a＜0且p是q的充分不必要条件，求实数a的取值范围。

解析：由p得(x-3a)(x-a)＜0，当a＜0时，3a＜x＜a。

由q得x2-x-6≤0或x2+2x-8＞0，解得x＜-4或x≥-2。

设A=(3a，a)，B=(-∞，-4)∪[-2，+∞)。

由p是q的充分不必要条件，可知AB，故a≤-4或3a≥-2，即a≤-4或a≥

又因为a＜0，所以a≤-4或≤a＜0，即实数a的取值范围为(-∞，-4]∪