基于微分方程的谣言传播模型建立与分析

赵 敏, 陈文霞

(江苏大学 理学院, 江苏 镇江 212013)

随着科技的迅猛发展,人与人之间的交流方式也产生着巨大变化.在线社交网络作为一种新型社交方式,为人们的生活和工作带来了极大的便利.然而,社交网络对虚拟人群约束较少,会存在许多非真实或者未经证实的消息,这就大大削弱了网络中各类信息的安全性和确定性,给社会稳定带来了极大的危害.因此,如何更好地掌握谣言传播机理、制定有效的谣言传播控制策略并最大限度减低谣言带来的危害,这些都是目前网络舆情研究领域急需解决的问题.

基于数学模型研究谣言传播机理已受到国内外学者的广泛关注.20世纪50年代,Landau等[1]首次提出了谣言传播与传染病传播的相似性理论.1965年,Daley等[2]借助传染病中“仓室”的思想,将谣言传播系统中的人群分成未知谣言人群、谣言传播人群及谣言免疫人群,并建立D-K模型,对谣言传播机理进行了初步研究.1973年,Maki等[3]在D-K模型的基础上,考虑到谣言传播之间相互接触产生影响,建立了M-T数学模型.随后许多学者对M-T模型进行改进,提出了一系列谣言传播模型[4-8].最近,余莎莎等[9]基于SIR模型的思想,考虑羊群效应以及信息老化效应,建立新型SIR模型,将其应用到商业谣言传播研究中.Zhao等[10]等考虑到遗忘机制对谣言传播的影响,建立了社交网络谣言时空传播SI模型,讨论了模型平衡点的存在性、平衡点的局部稳定性与全局稳定性等动力学问题;Zhu等[11]提出了一类噪声影响的谣言传播模型,分析了该模型的稳定性;Liu等[12]讨论了无标度网络上SEIR谣言传播模型的全局动力学;樊重俊等[13]建立了应急管理者对谣言传播影响的SIM模型,讨论了系统各类平衡点的稳定性;梁新嫒等[14]基于社交网络中媒体对谣言影响情况,建立ISMR模型,并且指出在媒体澄清谣言之后,谣言传播的衰减速度将会加快;赵洪涌等[15]建立了具有媒体报道效应的网络谣言传播模型,并分析了模型的稳定性和媒体报道对网络谣言传播的影响;陈颖等[16]讨论了网络舆论危机与治理.然而,上述研究工作很少考虑媒体宣传报道对谣言易感人群的影响.

基于以上分析,本文将考虑到官方媒体宣传的因素,将社交网络中的人群分为4类：未受官方媒体宣传影响的易感人群、受到官方媒体宣传的易感人群、谣言传播者以及谣言免疫者.通过分析受到官方宣传影响的易感者与未受到官方宣传的易感者之间的差别,建立新的SuSeIR谣言传播模型,用以研究具有媒体宣传报道影响的谣言传播机理问题.通过对所建模型各类平衡点稳定性研究,对谣言未来发展趋势进行预测和研判.

1 模型建立

本文在SIR模型的基础上,考虑易感人群对官方媒体宣传报道的接收情况,将易感人群分为未受到官方媒体宣传报道影响的易感者(其数量用Su表示)和受到官方媒体宣传报道影响的易感者(其数量用Se表示),在此基础上将社交网络上的人群分成4类：未受到官方媒体宣传报道影响的易感者Su；受到到官方媒体宣传报道影响的易感者Se；谣言传播者I,此类人会传播谣言；谣言免疫者R,并且不再传播谣言.谣言传播过程如图1所示.

图 1 谣言传播过程

基于此,关于上述SuSeIR模型作如下假设：

1) 进入社交网络的人群为易感人群;

2) 易感者是否会受到官方媒体报道影响,由受教育程度q决定,并且未受到官方宣传影响的易感者数量与受教育程度成正比.假设进入整个系统的人数为Λ,因此,进入系统的人数中,将会有qΛ人变成未受到官方宣传影响的易感人群,(1-q)Λ人将会变成受到官方媒体宣传的易感人群;

3) 媒体宣传程度的有效性σ会影响受官方媒体报道影响的易感人群变成传播者;

4) 随着时间的变化、社会认知的影响等会有一定概率γ的未受到官方媒体宣传报道影响的易感者、受到官方媒体报道的易感者、谣言传播者以及谣言免疫者离开系统;

5) 因自身意识等变化,有一定概率μ受到官方媒体报道影响者和谣言传播者变成谣言免疫者.

下面根据图1,对谣言传播的规则进行阐述：

1) 处在状态Su的人群,接触到谣言传播者之后,以概率β变成谣言传播者,根据假设2)和4),得状态Su的人群单位时间的变化数量可表示成

qΛ-βSu(t)I(t)-γSu(t);

2) 处在状态Se的人群,因受教育程度的限制,在媒体报道有效性的影响下,接触到谣言传播者之后以概率βσ变成谣言传播者.由假设2)、4)、5),可以描述出单位时间Se数量变化表达式为

(1-q)Λ-βσSe(t)I(t)-γSe(t)-μSe(t);

3) 处在状态I的人群,是由系统中状态Su和状态Sa的人群转变而成,根据假设4)和假设5),可以得出单位时间谣言传播者I的数量变化表达式为

βSu(t)I(t)+βσSe(t)I(t)-γI(t)-μI(t);

4) 根据假设4)和假设5)可知,单位时间内处在R状态的人群的数量变化表达式为

μSe(t)+μI(t)-γR(t).

基于微分方程建模思想,建立如下SuSeIR谣言传播模型

(1)

2 谣言传播模型动力学分析

2.1 平衡点存在性和基本再生数系统(1)总是存在边界平衡点

它表示网络中无谣言传播扩散,亦称为无谣言传播平衡点.

在边界平衡点E0处,借助下一代矩阵的方法,求出

V=

进一步计算可得基本再生数R0为

基本再生数R0=1下为谣言传播阈值.当R0<1时,谣言逐渐消失,不会扩散;当R0>1时,谣言会大范围扩散.

求得

令

求得

令

求得

而对于I*来说,满足下面一元二次方程

AI(t)2+BI(t)+C=0,

(2)

其中

A=β2σ(γ+μ),

B=(γ+μ)2β+(γ+μ)γβσ-

β2qΛσ-β2σΛ(1-q),

C=γ(γ+μ)2-(γ+μ)βqΛ-βσΛ(1-q)γ.

于是,(2)式的解为

1) 当R0<1时,C>0,且

γ(γ+μ)2>βσΛγ(1-q),γ(γ+μ)>βqΛ,

所以

γ(γ+μ)2+(γ+μ)γ2σ-

βqγΛσ-β(1-q)γΛσ>0,

即B>0.此时系统全为负根.故正平衡点E1不存在,即不存在有信息平衡点.

2) 当R0=1时,则C=0.通过简单的计算可知B>0,即系统有一零根和负根.因此原系统不存在正平衡点.

综上,可得下面结论.

定理 1当R0≤1时,系统(1)不存在正平衡点.

由于模型(1)前2个方程与变量R(t)无关,所以下面仅需讨论其等价系统

(3)

2.2 边界平衡点的稳定性分析

故其对应的系数矩阵为

J1=

求解得其特征根为

λ1=-γ,λ2=-γ-μ,

显然,λ1,λ2<0,又由于R0<1,所以

γ(γ+μ)2>βqΛ(γ+μ)+γβσΛ.

因此

γ(γ+μ)2>βqΛ(γ+μ)+γβσΛ(1-q),

即

证明构造Lyapunov函数

沿着系统(3)对时间t求导得

恒成立,当且仅当

I=0时等号成立,此时

由LaSalle不变原理知,边界平衡点E0全局吸引.综合定理1可得结论成立.

注 1定理2和定理3说明随着时间的推移,谣言不会大范围扩散,将逐渐消失.

2.3 正平衡点的稳定性分析

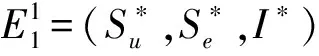
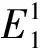
其对应的系数矩阵

J2=

其中

对应的特征函数

f(λ)=λ3+A1λ2+B1λ+C1,

其中

因为I*>0,所以,A1>0,B1>0,C1>0.因此,特征方程的特征根全为负.

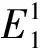
证明构造Lyapunov函数

对时间t求导得

γ+μ)Se(t)-(1-q)Λ)≤0.

当且仅当

时等号成立,此时

注 2定理4和定理5说明随着时间的推移,谣言将会大范围扩散.

3 数值仿真分析

例 1(边界平衡点的全局渐近稳定性) 在系统(1)中取q=0.5,Λ=0.2,β=0.15,γ=0.1,σ=0.05,μ=0.1.边界平衡点E0(1,0.5,0,0.5),基本再生数R0=0.768<1.由定理1和定理2可知,E0全局渐近稳定.使用Python软件作出相图,如图2所示.图2说明社交网络中谣言传播者最终消失,网络中不存在谣言传播现象.

例 2(正平衡点的全局渐近稳定性) 在系统(1)中取q=0.5,Λ=0.5,β=0.2,γ=0.1,σ=0.05,μ=0.1.简单计算可知,正平衡点E1=(0.940,1.200,0.829 8,2.030),且基本再生数R0=2.56>1,即定理4和定理5的条件成立,故E1全局渐近稳定,如图3所示.图3表明,谣言在网络中大范围扩散,给社会将带来极大危害.

4 谣言传播的控制策略

例 3(谣言传播的控制策略1) 在系统(1)中,取参数q=0.5,Λ=0.5,γ=0.1,μ=0.1,σ=0.05,保持易感者变成谣言传播者的概率β在[0.2,0.5]之间连续变化.使用Matlab软件绘制出谣言传播者数量随参数β变化的曲线,如图4所示.

图 2 系统(1)边界平衡点的全局渐进稳定性

从图4中可以看出,当β增加时,谣言传播者数量会增加,而β值减少时,谣言传播者数量会逐渐减少.因此,有关部门加大对谣言传播危害的的宣传报道,能有效地控制谣言传播者数量,最终降低谣言传播带来的危害.

例 4(谣言传播的控制策略2) 在系统(1)中,取参数q=0.1,Λ=0.5,β=0.2,γ=0.1,μ=0.1,并让媒体宣传有效性的参数σ在[0,0.5]内连续变化,使用Matlab软件,可以得到基本再生数R0随σ变化的曲线,如图5所示.从图5可以看出,当σ在一定范围取值时,基本再生数R0<1.适度的媒体宣传报道有助于谣言停止传播.当σ大于一定值时,基本再生数R0>1,此时谣言不会消失,将大范围扩散.这表明媒体的“过度”宣传报道使得人群产生逆反心理,可能会增强对谣言的相信,使得谣言传播者数量增加,有更多的人相信谣言,最终谣言不会消失.有关部门应该控制媒体宣传强度,使其处在适当的范围,保证最终谣言消失,降低对社会的危害.

图 3 系统(1)正平衡点的全局渐近稳定性

图 4 谣言传播者数量随β值变化曲线

例 5(谣言传播的控制策略3) 取参数q=0.6,γ=0.083,μ=0.1,σ=0.1,Λ=0.4,β=0.2,通过简单的计算可得R0>1.根据定理4和定理5知,系统(1)的正平衡点是全局渐近稳定性的,如图6(a)所示.进一步,选取谣言传播人群不同初值分别为：0.9、1.0、1.1、1.2、1.3、和1.4.图6中(b)描述了不同初始条件下,谣言传播人群数量的变化情况.该图表明谣言传播人群初始数量越小,谣言传播者到达峰值也越小,越有益于谣言的控制.所在谣言传播初期,宣传和管理部门就应该积极采取措施,控制谣言传播人群的数量,降低谣言传播带来的危害.

图 5 基本再生数数值随σ变化的曲线图

(a)

(b)

5 结论

本文考虑谣言传播过程中官方媒体宣传对谣言易感者的影响,将谣言易感者分成两类,构建了一类新的谣言传播动力学模型.该模型的理论分析仿真表明,媒体的适时宣传报道,能降低谣言感染率,遏制谣言的传播并最终消失.对于传播阈值超过1的谣言,政府部分要重点监控其发展状况,在谣言传播的初期就进行积极宣传和引导,控制谣言传播者数量,把谣言事件的负面影响降到最低.