Belitskii约化与三阶矩阵对的标准形
2019-11-06蔡红艳
章 超, 蔡红艳
(贵州大学 数学与统计学院, 贵州 贵阳 550025)
令k为代数闭域.箭图的表示理论在众多学科中有重要应用,例如动力系统理论.一个经典的应用来源于文献[1].令Qi/s/o为系统箭图,其中Q0:={1,2,3}以及Q1:={α:1→2,β:2→2,Γ:2→3}.Qi/s/o的一个表示(G,F,H)对应于方程x(t+1)=Fx(t)+Gu(t),y(t)=Hx(t),其中t∈Z,x(t)∈kn,u(t)∈km且y(t)∈kp.该系统空间的正则点以及满足特定条件的标准型得到了深入研究,见文献[2-3].
从表示理论的角度来看,上述系统箭图的表示理论很复杂,是最典型的野表示型代数,在表示型的研究中扮演着重要的角色[4-6].由Gabriel图化定理,代数Γ≅kQ,其中Q为

,


H={S∈GLn(k)|SJ=JS},
因而这个问题的研究涉及与给定矩阵可交换的矩阵问题[7].
通常来说,描述野代数的表示的同构类是非常困难的[8-10].本文主要利用Belitskii约化算法研究代数Γ的低阶表示的同构类问题,即三阶矩阵对的标准形问题.
1 Weyr标准形与Belitskii约化
研究矩阵对(A,B)的标准形,涉及与矩阵A的标准形JA可交换的矩阵问题.在研究与矩阵JA可交换矩阵问题中,矩阵的Weyr标准形比Jordan标准形更为方便.

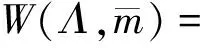

引理 1.2[12]设
J(Λ)=Jedd(Λ)⊕Jed-1d-1(Λ)⊕…Je11(Λ)




Λ={X=(Xij)d×d∈GLn(k)|Xij=0(i>j);
其中Π(Λ)为指标集.方程组
称之为集合Λ的定义方程组.另外,Λ也决定了集合T={1,2,…,d}上的等价关系~:i~j当且仅当线性方程xii-xjj=0属于E(Λ).


下面的引理可以直接验证可得.
引理 1.5如果n阶方阵M=(Mij)d×d的子块Mij是Λ-稳定的,那么当ij时,Mij=0;否则,Mij=aijI为纯量矩阵.

由Mlr的最小性与引理1.5可知
定义线性方程
(*)
下面对可能的3种情形进行讨论:
1) 如果方程组E(Λ)不蕴含方程(*),则必存在X∈Λ,使得(X-1MX)lr=(M1)lr=0.

3) 如果方程组E(Λ)蕴含方程(*),且lr,则必存在X∈Λ,使得Xrr≠Xll且方程(*)简化为其中s=rankM.



情形2Λ1={X=(Xij)d×d∈Λ|W1Xrr=XllW1};


2 三阶矩阵对的相似标准形
本节将利用上节中介绍的Belitskii算法计算三阶矩阵对的相似标准形,从而给出三阶矩阵对的相似分类.
当矩阵对(A,B)中A、B都为三阶矩阵时,以矩阵A的Weyr标准形进行分类讨论,共有以下6种情形.
情形1A相似于ΛI3.这种情形下,Λ=GL3(k),即所有的三阶可逆矩阵构成的集合.对于矩阵B,则存在可逆矩阵X,使得X-1BX=W1为三阶Weyr标准形,所以

则
令矩阵
则约化过程中要满足



a31x13+0×x11=x11×0,
故x13=0.因此
注意到此时B3已经Λ3-稳定了,因此
如果a31=0,则讨论过程更为复杂.记
W2=W(Λ,(1,1,1)).
类似上面的讨论,利用Belitskii约化算法,按照上节中定义的序依次对变量aij逐一进行讨论,可以得到如下可能的标准形:
另外4种情形的约化方法类似,下面给出矩阵对(A,B)约化后的可能标准形.记r(b)= rank (b)为b的秩,即若b≠0,则r(b)=1;否则r(b)=0.




3 Belitskii标准形的参数数
令(M,Λ)为前面小节中的线性矩阵问题,其中M为满足特定条件矩阵M构成的代数簇,代数群G={S∈Λ|det(S)≠0}通过共轭作用在这些矩阵M上,矩阵M的G-轨道OM即为M的Λ-相似类,M的稳定子群为
StabG(M)={S∈G|S-1MS=M}.
对于维数,有dimG=dimOM+dimStabG(M).令ind(M)为M中的不可分解矩阵,这里的不可分解矩阵表示非准对角矩阵.令
inds(M)={M∈ind(M)|dimOM=s}.
下面的定义可参见文献[14].
定义 3.1ind(M)在群G作用下的参数数定义为

线性矩阵问题按照复杂度分为驯表示型与野表示型,参见文献[11],粗略地说,驯表示型的线性矩阵问题(M,Λ)即为M中任意给定型号的矩阵可以由单参数量化,而野表示型矩阵问题包含了古典矩阵对的标准型问题,被认为是没有希望完全解决的.
定理 3.2[15]ind(M)在群G作用下的参数数μ(ind(M))为线性矩阵问题(M,Λ)的Belitskii标准形中所含参数的极大值,而且线性矩阵问题(M,Λ)为驯表示型当且仅当μ(ind(M))≤1.
将上述定理应用到三阶矩阵对的约化问题,结合上节计算的Belitskii标准型,可以得到下面命题.
命题 3.3设(M,Λ)为前面小节中的线性矩阵问题,则μ(ind(M))=6.特别地,(M,Λ)为野表示型的线性矩阵问题.
