基于半监督最大间隔字典学习的故障诊断方法*

王维刚, 陶 京, 刘占生

(1.东北石油大学机械科学与工程学院 大庆, 163318) (2.哈尔滨工业大学能源科学与工程学院 哈尔滨, 150001)

引 言

随着工业自动化程度的提高，机械设备越来越复杂，从中获取故障数据非常困难，而且付出的代价也是巨大的。与此相反，机器在服役内绝大多数时间运行是正常的，因此获取设备正常工况数据是非常容易而且廉价的。基于可获得数据是否带有标签，可将机械故障分类分为监督和非监督两类[1]。当正常和故障状态的先验信息可获得时，可用监督方法进行故障分类；相反若没有先验信息，需要采用非监督方法。当机械设备发生故障时，振动信号将会偏离正常值，而基于振动信号的诊断技术已广泛用于轴承[2]、齿轮[3]等设备的故障诊断中。近年来，稀疏编码技术在人脸识别[4]、图像分类[5]等领域的成功应用，文献[6-8]将其引用在机械故障诊断中，例如：文献[6]采用稀疏编码提取特征以进行机械故障诊断；文献[7]将稀疏自动编码器融入深度神经网络，实现非监督学习的特征提取，感应电动机的故障诊断试验验证了方法有效性；文献[8]提出了用于机械故障分类的半监督类标一致字典学习框架，采用类标一致字典学习和自适应类标预测联合的技术，故障诊断实验验证了方法的优秀性能。

对于信号处理，稀疏编码采用过完备字典中几个原子的线性组合近似表示输入信号，其中字典的质量决定稀疏编码的性能。采用从训练样本中学习字典取代传统Fourier基或小波基进行编码，取得了非常好的效果。为了能够得到较好表示信号的字典，学者们提出了一些有效的字典学习方法[9-13]，并证明了由监督学习构建的字典能产生较好的分类性能，其中典型的监督字典学习方法包括判别k均值奇异值分解(discriminative k-mean singular value decomposition，简称D-KSVD)[12]，类标一致k均值奇异值分解(label consistent k-mean singular value decomposition，简称LC-KSVD)[13]。D-KSVD将分类误差添加至k均值奇异值分解(K-mean singular value decomposition，简称 KSVD)目标函数中，以增强字典的表示能力。LC-KSVD通过增加判别稀疏编码误差以提高KSVD模型的字典学习性能，并且由判别稀疏编码误差、重构误差和分类误差形成联合问题。由于D-KSVD和LC-KSVD均为监督模型，因此存在某些明显的缺点，如过拟合导致的性能下降以及实际中缺乏信号先验知识而导致的应用受限。现场无标记振动数据容易获得，若联合有标记和无标记数据来近似数据集几何结构，可以增强表示能力和分类准确度，这也正是半监督学习能引起学者们[14-15]广泛关注的原因。

为了探索更有效的字典学习算法，本研究在最大间隔字典学习(max-margin dictionary learning，简称MMDL)[16]算法基础上，将廉价的、易获得的无标记样本构成的重构误差项引入到目标函数中，所提出SSMMDL算法定义的目标函数不仅包括有标记样本的重构误差项、支持向量机的损失函数和分类间隔两个正则项，而且包括无标记样本的重构误差项，不但实现了字典和分类器的同步学习，而且能利用标记样本充分表达数据的潜在结构。

1 字典学习和稀疏编码

在训练阶段，已知输入信号集X=[x1，…，xN]∈Rm×N，求解过完备字典解的过程称为字典学习，如式(1)所示

(1)

字典学习是在满足稀疏度约束条件下使重构误差最小而获得的。KSVD[9]是一种求解式(1)的有效算法，通过将其分解为字典学习和稀疏编码两个子问题，并采用交替优化策略求解。

在测试阶段，已知字典D，求解测试样本xt对应稀疏向量st的过程称为稀疏编码，表示为

(2)

稀疏编码通常利用追踪算法来求解，包括匹配追踪(matching pursuit，简称MP)[17]、正交匹配追踪(orthogonal matching pursuit，简称OMP)[18]以及基追踪(basis pursuit，简称BP)[19]，此类方法计算简单、收敛快且能得到全局最优解。笔者采用OMP算法对测试信号进行稀释编码。

2 半监督字典学习算法

为了充分利用大量廉价的、易获得的未标记样本，笔者提出半监督最大间隔字典学习算法，将未标记样本构成的重构误差项也引入到最大间隔字典学习算法的目标函数中，具体模型如下所述。

2.1 优化模型的建立

记类别标签向量V=[y1，…，yN]，根据上述思想，将目标函数定义为

(3)

其中：Nu和Nl分别为无标记和有标记训练样本的数量；xu和xl分别为样本来自无标记数据集和有标记数据集；su和sl分别为xu和xl的稀疏表示。

式(3)前两项均为重构误差项，第3项为支持向量机分类间隔正则项，第4项为损失函数项。系数α,β和γ控制上述项的权重。该目标函数包括D,S,[ω，b](ω和b看作一个整体)3个决策变量，式(3)对于上述3个变量不是凸函数，但是当固定其中任意两个变量后，目标函数为凸函数。

2.2 模型的求解算法

当振动信号输入模型时，采用在稀疏编码、字典更新及支持向量机参量三者之间交替进行的方式求解上述模型。

首先，初始化字典D及支持向量机参量[ω，b]。该过程是在有监督条件下实现的。为了满足字典每个基向量都与某一故障类别有关，先采用文献[20]算法学习多个故障类别对应的子字典，然后将其合并为完整过完备字典，其形式如下

D=[D1，…，Dk，…，DM] =[d1,1，…，d1,L，…dk,1，

…，dk,L，…dM,1，…，dM,L] ∈Rm×K

(4)

其次，在t次迭代时，固定D,[ω，b]，求样本xt的解稀疏表示st。若xt为无标记样本，则直接采用OMP算法求解式(2)即可；若xt为有标记样本，则稀疏编码问题转换为

(5)

除去与st无关的项，化简后的目标函数为

(6)

该目标函数的梯度和Hessian矩阵分别如式(7)和式(8)所示。

▽J(st)=-2αDTxt+2αDTDst+

2γωωTst+2γbωUT-γωVT

(7)

▽2J(st)=(2αDTD+2γωωT)⊗I

(8)

其中，U=[1，…，1]∈R1×N。

该目标函数的Hessian矩阵半正定，因此目标函数J(st)为凸函数，即优化模型为一个有约束的凸优化问题，采用拉格朗日-拟牛顿法便可求得全局最优解。

算法1：字典更新

步骤1：输入当前字典Dt-1，初始化j=1，计算At和Bt

(9)

(10)

步骤2：更新字典的第j列，公式为

(11)

(12)

步骤3：j=j+1，返回步骤2，直至j=K。

步骤4：重复步骤2～步骤3，直至收敛。

最后，固定S,D，更新参量[ω，b]。式(3)变为

(13)

上述模型为一个标准的支持向量机分类问题，可采用共轭梯度等方法来求解。

2.3 无标记样本学习

关于无标记样本属于故障中的已有类别还是新类别，文中采用基于信号稀疏编码概率模型的选择准则进行判断。

考虑输入信号x的稀疏表示s=[s1，…，sK]T。一旦子字典确定了其类别，就不会再变。此时可用与基向量dj相关的稀疏系数sj计算信号x处在与字典基向量dj同一类别的概率。将同一类与字典基向量相关稀疏表示的绝对值加起来并归一化，就得到信号的类别概率分布。具体讲，假设有M类分类问题，每类用L个基向量表示，L×M=K。已知字典D，信号x属于类别l的概率为

(14)

其中：L为一个数据点或字典基向量映射到一个特定的类标签l∈{1，…，M}。

计算信号x的类概率分布公式为P(x)= [p1(x)，…，pM(x)]T。概率分布表示字典区分输入信号的能力。为了量化输入信号区分性的置信度，计算其稀疏表示的熵

(15)

如果字典对某输入信号有高的区别性，则期望稀疏表示的较大值集中在某字典基向量上，因此该信号的类别就最大可能地属于与字典基向量对应的类别。从定量角度，设置概率分布的两个熵阈值：上限值φh和下限值φl。如果信号熵值比下限值φl小，表明该信号关于当前字典是一个区分性强的输入信号，且由此确定该信号的类别。于是该信号自动添加到有标记数据集中，进一步求解新字典。如果信号熵值比上限值φh高，有两层含义：a.该信号是不确定信号；b.当前字典不能很好地表示该信号。该不确定点可能靠近决策边界，也可能为新类别数据，因此对于字典学习这些信号是非常关键的。首先用训练数据的稀疏表示近似其类属性，然后产生熵值分布作为确定阈值的基础。按照手动标记预估上限值φh，最优的φl通过对训练集5次交叉验证来确定。模型中α,β和γ也通过交叉验证来确定。

概括提出的半监督最大间隔字典学习策略。先在完全监督下初始字典及支持向量机参量;随着未标记训练样本依次输入，给定当前字典，计算稀疏表示的概率分布，并评价样本的置信度。如果熵值低于下限值，自动标记该样本为对应类别。在极少情况下，如果熵值超过上限值，要求用户标记该数据新的类别。若样本熵值位于上限值与下限值区间，则将其从样本中删除。算法2为本算法的伪代码。

算法2：半监督最大间隔字典学习策略

输入：训练样本X=[x1，…，xN]和对应标签V，系数α,β和γ，上限值φh和下限值φl。

输出：D和[ω，b]。

初始化：初始化D0[ω0，b0]，A0=0，B0=0。

fort=1，…，N

输入训练样本xt

ifxt是无标记样本

用式(2)计算其稀疏表示st

用式(15)计算Ent(xt)

ifEnt(xt)<φl

L(xt)=argmaxjpj(x)

用算法1更新字典Dt

elseifEnt(xt)>φh

L(xt)=l

endif

endif

用式(5)计算其稀疏表示st

用算法1更新字典Dt

用式(13)更新[ω，b]

endfor

2.4 基于稀疏表示的分类方法

记测试样本为xt，从算法2得到字典D，根据式(2)计算其稀疏表示st。当st在字典上的响应满足式(16)时，则判定该测试样本属于第k类

(16)

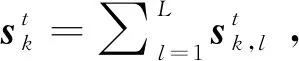
3 故障诊断方法的过程

基于半监督最大间隔字典学习的故障诊断流程如图1所示，该方法主要包括以下步骤：

图1 基于半监督最大间隔字典学习的故障诊断流程Fig.1 Flowchart of fault diagnosis based on semi-supervised max-margin dictionary learning

1) 先用多结构元素差值形态滤波器对原始振动信号(包括训练和测试信号)降噪[21]，再用平滑伪维格纳-威尔分布(smoothed pseudo wigner-ville distribution，简称SPWVD)[22]技术将时域信号转换为时频表示;

2) 采用三次样条插值方法[23]压缩时频表示，构建故障样本;

3) 将有标记和无标记高维训练故障样本输入到半监督最大间隔字典学习算法中，输出字典;

4) 对测试样本，经稀疏编码后得到对应稀疏表示，采用基于稀疏表示的分类方法识别测试样本的类别标签。

4 实例分析

本试验数据来自模化汽轮机转子试验台，如图2所示。该试验台包括动力系统、转子系统、润滑系统及振动信号采集分析系统4部分，其中转子系统由3跨转子、两个轮盘、一个模化太阳轮转子、3个联轴器及4个滑动轴承(其参数为长径比为0.625、半径间隙比为2‰、轴承直径为40 mm)组成。在4个轴承上分别安装两个BENTLY 3000XL8 mm电涡流位移传感器，用以测量轴承水平和垂直方向振动信号。采样频率为1 600 Hz，在转速为3 000 r/min下分别测取正常状态、不平衡故障、不对中故障、地脚松动故障、径向碰磨故障及油膜涡动故障(分别记为f1,f2, …,f6)6种工作状态的振动信号各200组，任选100组为训练样本，剩余100组为测试样本。其中，正常状态的样本是在转子安装调试、动平衡后采集的样本；不平衡故障样本是在两个轮盘零相位处的平衡孔上分别添加5， 10 g不平衡配重后采集的样本；不对中故障样本是在抬高中间两个轴承标高0.08 mm后采集的样本；地脚松动故障样本是在松动中间两个轴承地脚螺栓后采集的样本；径向碰磨故障样本是利用摩擦棒与轮盘发生碰磨后采集的样本；对于油膜涡动故障，是转速升高至一阶临界转速之上，而未达到一阶临界转速二倍时采集的样本。图3，4分别为转子油膜涡动故障的时域波形图、频谱图、SPWVD时频图像及压缩图像。

图2 模化汽车机转子试验台Fig.2 Modelling steam turbine rotor test stand

图3 油膜涡动故障的时域波形图及频谱图Fig.3 Time domain waveform and frequency spectrum of oil whirl fault

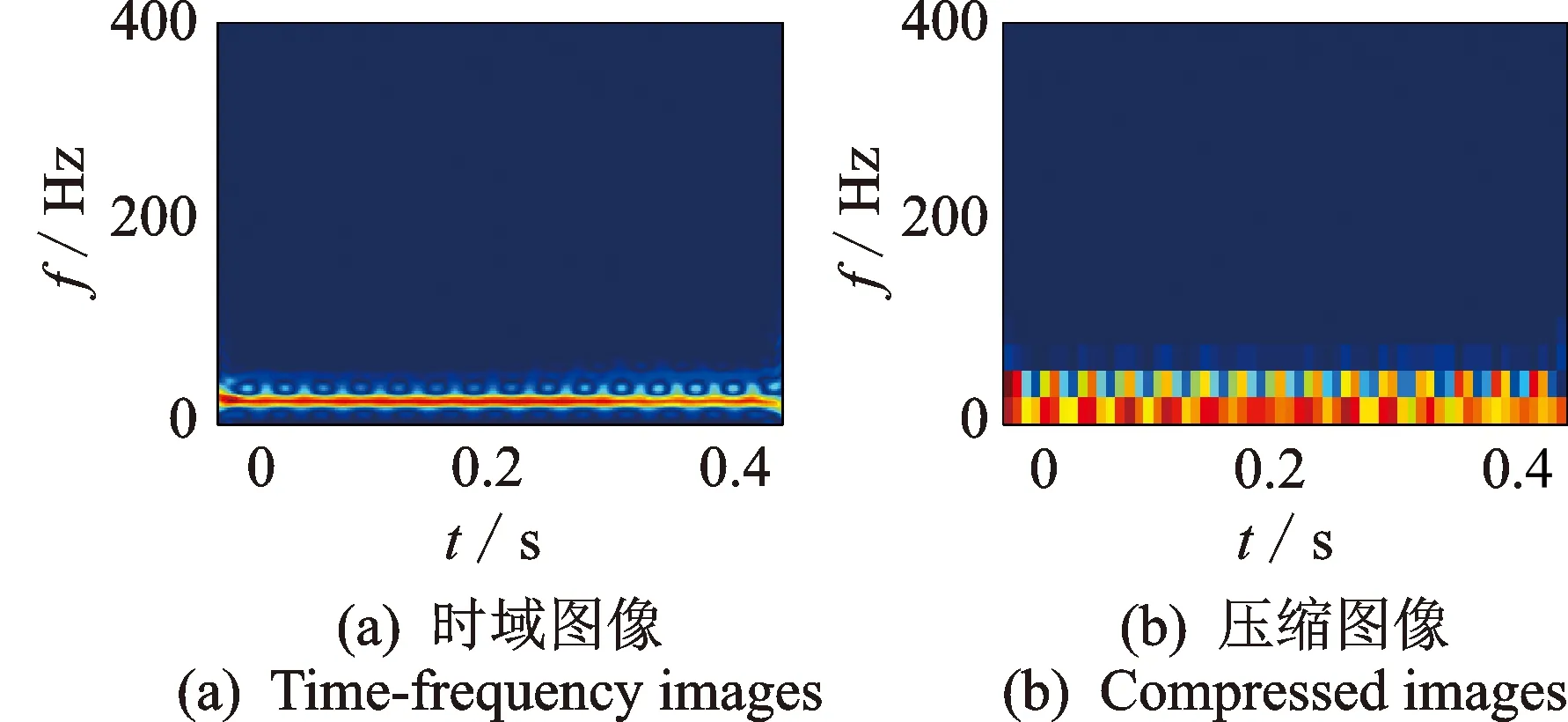
图4 油膜涡动故障的SPWVD时频图像及其压缩图像Fig.4 SPWVD time-frequency images and compressed images of oil whirl fault

为了减小数据规模，在半监督字典学习前，采用图像缩放技术中的双三次插值算法，将SPWVD1024×1024时频矩阵压缩至30×30矩阵，如图4所示。为防止过度拟合的产生，本算法所有系数的选取均采用交叉验证法自动完成。另外，为了保证结果的客观性及对比的公正性，所有试验结果均为运行20次后的平均值。为防止产生过拟合现象，所提算法中的3个正则项系数均采用交叉验证法自动选取。关于熵阈值上限值φh和下限值φl确定，先采用训练数据的稀疏编码来粗略估计其类别分布，通过熵值分布确定φh为0.6，从而进行人工标记，而最优φl值可对训练数据集通过交叉验证法进行选择。本算法所得计算结果均为独立运行20次的平均值，以确保结果的客观性。现从以下3个方面分析笔者所提方法的有效性。

1) 分析时频字典的特性。从训练集选取压缩时频图像进行子字典学习，其中子字典长度为30，原子个数为5，经SSMMDL算法得到转子6种工作状态的子字典(如图5)。可以看出，每种工作状态对应的时频原子波形都有瞬时脉冲，但是每类子字典对应的脉冲幅值大小均不相同，这样不同故障的测试样本就得到不同的稀疏编码，为故障识别奠定基础。

图5 从转子振动数据得到的各类子字典Fig.5 Sub-dictionary of each class learned from rotor vibration data

2) 针对所提方法，验证未标记样本对故障诊断性能的改善状况，以及有标记样本与未标记样本不同比例对性能的影响规律。在100组训练集中分别选择有标记样本数为40,60和80，并设置不同未标记样本数，测试不同比例下所提方法的分类准确率，并将其与仅采用有标记样本(对应未标记样本数为0)的最大间隔字典学习算法进行对比，结果见表1。

通过表1的试验结果可以看出，未标记样本的加入使故障诊断准确率得到提高；训练样本总数相同，但未标记和有标记样本数比例增加时，故障诊断准确率也随之增加；故障诊断准确率随有标记样本数增加而增加。从训练样本中包含的有标记样本数和无标记样本数来看，基于SSMMDL半监督字典学习算法的识别率高于有监督学习算法的识别率，而且随着未标记样本数的增加，算法的识别率随之提高，验证了方法的优越性。

3) 将所提方法SSMMDL与MMDL,LC-KSVD,D-KSVD、稀疏表示分类器(sparse representa-tion based classifier，简称SRC)[21]进行对比，以进一步验证所提方法的优越性。设置φhigh=φlow=0，即所有新样本全部进行标记，SSMMDL与其他几种字典学习方法的对比结果如图6和表2所示。可以看出，笔者所提方法的识别率优于其他方法，尤其当有标记样本数较少时，所提方法更显示了优越的性能。MMDL是一种有监督的最大间隔字典学习，仅利用有标记样本实现字典和分类器的同步学习，因此分类性能低于SSMMDL。D-KSVD和LC-KSVD2均为监督方法，利用有标记样本进行训练和分类，因此分类性能尚可。由于SRC是一种无监督方法，分类性能最差。而从运行效率角度，尽管所提方法的运行时间比其他3种方法耗时稍多，但完全可以满足在线监测的要求。通过上述的对比分析可知，基于SSMMDL的半监督字典学习算法体现了一定的优越性。

表1 不同有标记样本和未标记样本比例下SSMMDL算法的分类性能

图6 SSMMDL与其他方法的识别率随样本数的变化趋势Fig.6 Change trend of recognition rates of SSMMDL and other three methods with labeled sample number

Tab.2 Classification performance of SSMMDL and other methods

方 法t/s最高识别率 /%SRC0.13693.30D-KSVD0.11794.32LC-KSVD20.12196.10MMDL0.25396.55SSMMDL0.31098.89

5 结束语

笔者提出一种基于SSMMDL算法的故障诊断方法。首先，从原始振动信号的SPWVD分布中提取时频域特征，并构建训练样本集；然后，通过所提SSMMDL算法从训练样本集学习字典；最后，通过字典求解测试样本的稀疏表示，并利用基于稀疏表示的分类器实现故障模式识别，得到测试样本的故障类型。运用时频分析方法构建高维故障样本，该样本能揭示非平稳信号的频率成分及时变特征，为构建判别性较强的字典打下基础。所提方法能够充分利用无标记样本的信息，通过将无标记样本稀疏重构误差项添加至优化模型，提高了故障诊断模型的判别能力。试验结果表明，随着未标记样本数量的增加，故障识别率随之提高。转子故障诊断结果验证了所提半监督字典学习算法的优越性，相比其他算法，不但提高了识别率，而且能用于在线监测中。