半柔性阀压电泵理论与实验*

付 俊， 张建辉， 王 颖， 严秋锋

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016) (2.航空工业洪都650所 南昌，330024) (3.广州大学机械与电气工程学院 广州，510006) (4.泰州职业技术学院机电技术学院 泰州，225300)

引 言

压电泵利用压电振子能够将电能转化为机械能这一特点，并把力和运动施加在流体上，实现了以往机械传动的功能。通过控制阀体实现流体的单向运输、改变流体的速度或压强。对于这种新型流体驱动器在微机电系统、医疗及生物化学等领域能够满足流量精确管控、噪音低以及微型化等要求。

Narasaki[1]设计了最初的压电泵，曾平等[2]提出了整体开启阀压电泵可实现微流量输送，但该泵的阀体部分和阀座部分固定工艺繁琐。Ham等[3]设计的板式铰链阀压电泵，可使用电子冷却循环设备。张建辉等[4]提出了利用内外不等锥度的软质锥壳形单阀体，但阀体占用空间较大，不易微型化。Stemme等[5]提出的锥形流管无阀压电泵，利用锥形流管作为无移动部件阀，替代了传统意义上的阀来实现流体的输送，避免了泵阀跟从性差。其他无阀压电泵用流管有TESLA管[6]、漩涡管[7]、Y型管[8-10]和三通扩散/收缩管[11]等，但有较大回流，导致流量不是很大。为克服上述问题，笔者设计了一种类静脉瓣结构阀，它属于材料为刚性，结构上呈现柔性的阀，并将这种阀体安装在压电泵流道内形成半柔性阀压电泵。

1 泵阀结构设计

图1为笔者设计的半柔性阀结构。该阀由阀体、定位器和两个铰链组成，阀的制作材料为紫铜。图2为半柔性阀压电泵结构。此泵主要部分为压电振子、泵体、泵盖及半柔性阀等。在进/出水口流道两侧对称安置半柔性阀。导管b一侧为吸入阀，导管a一侧为排出阀。

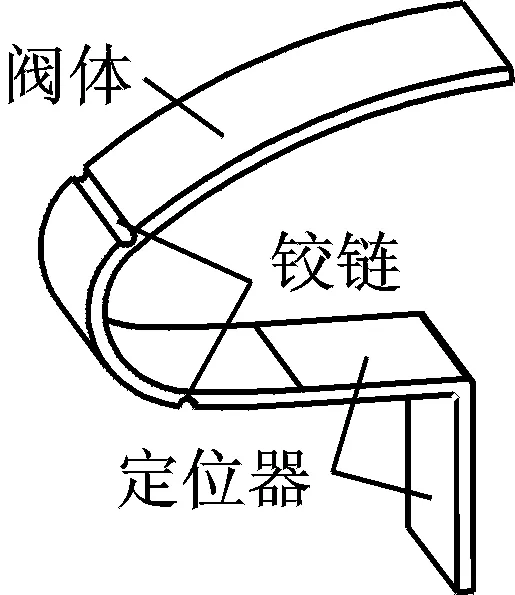
图1 半柔性阀结构示意图Fig.1 Schematic diagram of semi-flexible valve

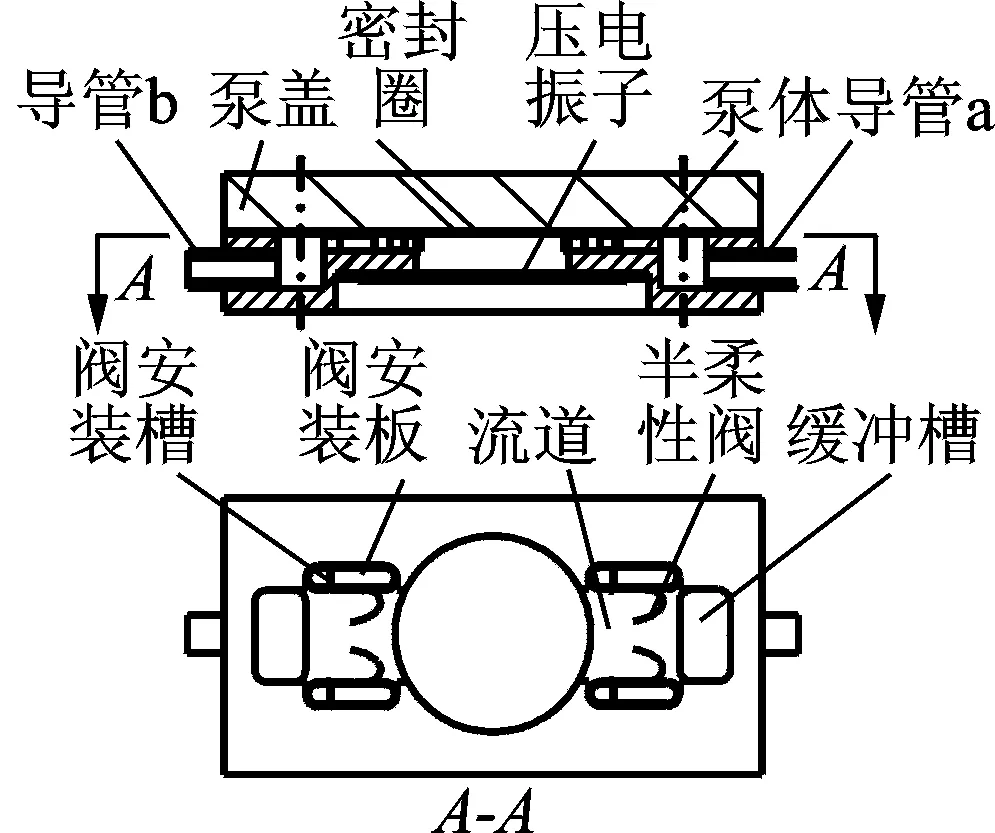
图2 半柔性阀压电泵结构示意图 Fig.2 Schematic diagram of piezoelectric pump with semi-flexible valve

2 泵的工作原理

如果无阀压电泵定义为在一个工作循环周期内，进出口的流道在任何时刻都是相连通的，没有被阻隔，那么有阀压电泵则在一个工作循环周期内，进出口的流道至少在某一瞬间被阻隔。半柔性阀压电泵是一种通过改变泵的输入(频率、电压)，而其他条件不变，可以实现有阀压电泵和无阀压电泵两种状态，并得到一定的输出。图3为半柔性阀压电泵常开时无阀状态工作原理示意图。压电振子的电压范围为0～U1，具体工作过程如下。

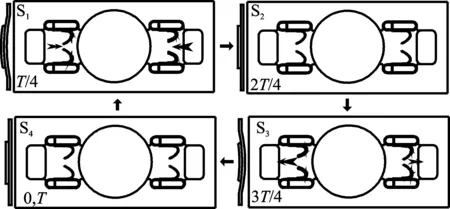
图3 半柔性阀压电泵无阀状态工作原理图Fig.3 Valve less working principle diagram of semi-flexible valve piezoelectric pump

第1阶段(0～T/4)：压电振子施加电压连续上升，其从起始位置不断凸起变形到最大变形处，腔内开始具有负压，两个吸入阀出现形变，两者间距增大，同时两个排出阀也出现形变，两者间距减小，流体由吸入阀和排出阀同时进入。

第2阶段(T/4～2T/4)：压电振子电压逐渐减小，同时其形变减小，腔内压力变大，吸入阀和排出阀的形变减少，泵腔中部分流体由吸入阀和排出阀排出。

第3阶段(2T/4～3T/4)：压电振子所施加电压连续上升，其从起始位置不断向下变形到最大变形处，腔内压强持续增加，两个吸入阀出现形变，两者间距减小，同时两个排出阀也出现形变，两者间距增大，泵腔中部分流体持续由吸入阀和排出阀排出。

第4阶段(3T/4～T)：压电振子电压在逐渐减小，同时其形变变小，腔内压力逐渐下降，吸入阀和排出阀形变不断减少，有流体由吸入阀和排出阀回流。

当泵从S3→S4→S1过程中，泵腔容积持续增加，腔内出现负压，此时两个排出阀的间距从最大距离不断发生形变，直到两者间距最小，两个吸入阀的间距从最小距离不断发生形变，直到两者间距最大，流体通过吸入阀和排出阀被吸入泵腔，该过程是吸程。当泵从S1→S2→S3过程中，泵腔容积持续变小，腔内压力持续变大，此时排出阀的间距从最短间距逐渐发生形变，直到两者间距最大，吸入阀的间距从最大逐渐变形，直到两者间距最小，流体通过吸入阀和排出阀被排出泵外，该过程是排程。

在吸程过程中，阀由于泵腔有负压而产生形变，吸入阀的阀的迎面流阻持续降低，排出阀的迎面流阻持续增大，而阀在原始未形变前，阀的迎面流阻反向比正向大，因此，吸入阀产生的流阻远小于排出阀产生的流阻，而对应的阀流进的流体量却相反。同理，在排程过程中，吸入阀产生的流阻远大于排出阀产生的流阻，而对应的阀流进的流体量却相反。所以泵由吸入阀吸入的流体大于排出的，由排出阀排出的流体大于吸入的，因此泵可以实现流体宏观的单向运输。

半柔性阀压电泵有阀状态工作原理如图4所示。压电振子电压范围为U2～U3，具体工作过程如下。

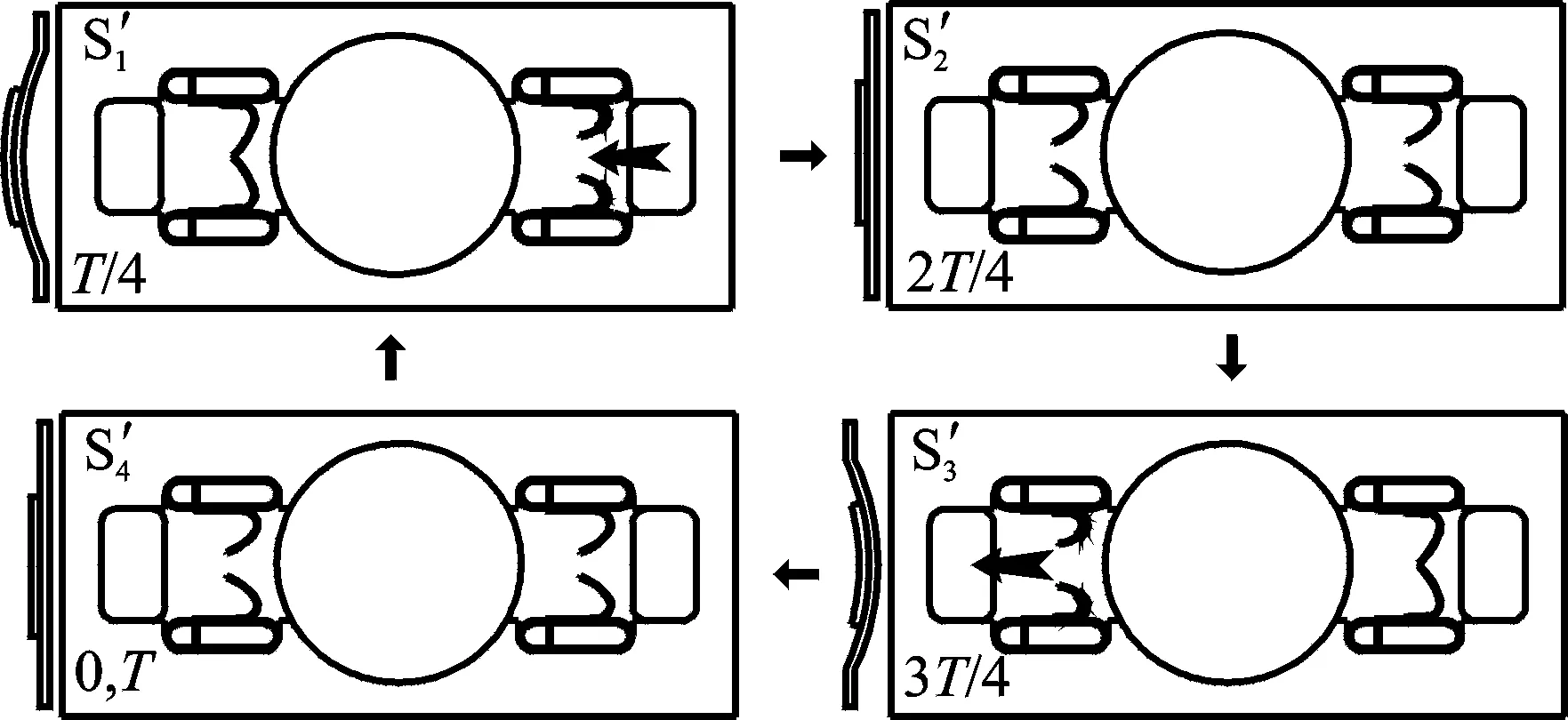
图4 半柔性阀压电泵有阀状态工作原理图Fig.4 Valve working principle diagram of semi-flexible valve piezoelectric pump

第1阶段(0～T/4)：压电振子所施加电压连续上升，其从起始位置不断凸起变形到最大变形处，腔内开始具有负压，两个吸入阀出现形变两者间距增大，同时两个排出阀也出现形变，两者靠拢闭合，流体由吸入阀进入。

第2阶段(T/4～2T/4)：压电振子电压在持续下降，同时其形变减少，腔内压力升高，排出阀和吸入阀形变持续减少，腔内部分流体从排出阀和吸入阀送出。

第3阶段(2T/4～3T/4)：压电振子所施加电压连续上升，其从起始位置不断向下变形到最大变形处，腔内压强持续增加，两个吸入阀出现形变，两者靠拢闭合，同时两个排出阀也出现形变，两者间距增大，泵腔中部分流体由排出阀排出。

第4阶段(3T/4～T)：压电振子电压持续下降，同时其形变减少腔内压强持续下降，排出阀和吸入阀形变不断减少，有流体由吸入阀和排出阀回流。

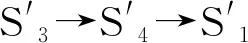
3 理论分析

半柔性阀可以简化成如图5所示的伪刚体模型。在两段圆弧连接点形成特征铰链，并分布扭转弹簧，扭簧的弹簧常数分别为k1和k2。在吸程阶段，阀在进水口处流道内某阶段受到大小为q(t)的压力，如图5所示。在排程阶段，阀同样受到一个大小相同，方向相反的压力，如图6所示。通过控制电参数实现阀的变形大小，从而实现半柔性阀的功能，达到其对流体进行控制。

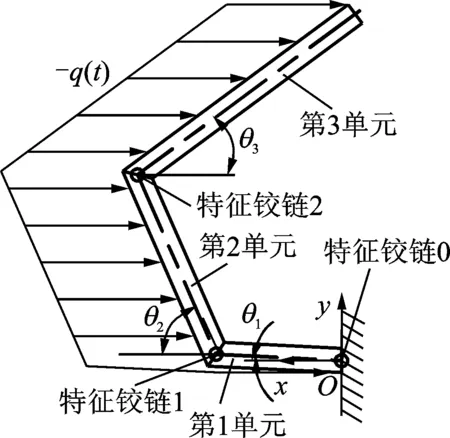
图5 伪刚体模型正向受力模型Fig.5 Forward force model of pseudo rigid body model

图6 伪刚体模型反向受力模型Fig.6 Reverse force model of pseudo rigid body model

吸程阶段，特征铰链1所受扭矩为

T1=-0.5q(t)(L2sinθ2+L3sinθ3)2

(1)

Δθ1=T1/k1

(2)

其中：L2，L3分别为第2，3单元的长度。

扭转弹簧1转动引起的刚体位移为

(3)

吸程阶段，特征铰链2所受扭矩为

T2=-0.5q(t)[L3sin(θ3+Δθ1)]2

(4)

Δθ2=T2/K2

(5)

扭转弹簧2角变形引起的刚体位移为

(6)

扭转弹簧1角变形引起的刚体位移为

(7)

在x和y方向上的总位移为

(8)

排程阶段，特征铰链1所受扭矩为

T3=0.5q(t)(L2sinθ2+L3sinθ3)2

(9)

Δθ3=T3/k1

(10)

扭转弹簧1转动引起的刚体位移为

(11)

排程阶段，特征铰链2所受扭矩为

T4=0.5q(t)[L3sin(θ3+Δθ3)]2

(12)

Δθ4=T4/k2

(13)

扭转弹簧2角变形引起的刚体位移为

(14)

扭转弹簧1角变形引起的刚体位移为

(15)

在x和y方向上的总位移为

(16)

k1和k2近似值分别为

(17)

(18)

其中：E为弹性模量；I2，I3分别为第2，3单元的惯性矩；γ2，γ3分别为第2，3单元的特征半径系数。

扭矩的计算不精确会给后续计算带来很大误差。此误差的根源在于计算是基于最新的变形位置、而不是最终的变形位置进行的。因此，可以利用载荷增加技术和迭代法减少此误差。

载荷增加技术是通过逐步增加外载荷进行的。这意味着要施加一定比例的外载荷，并应用链式算法求出其变形。该方法可以大大提高链式算法的计算精度, 尤其是相对较大的变形。随着载荷增加数的增多, 半柔性阀变形计算的精度将会提高。

如果上述两种方法相互结合，能在一定程度提高计算精度。根据最终的载荷增加计算出来的变形来估算新的利弊和满外载荷引起的新变形，直至计算要求为止。根据实际情况，可以对迭代的次数和载荷增加做出相应的调整。

在半柔性阀压电泵工作时，无论何种工作状态，其进出口都有一个名义上的阀开启或关闭以达到流体的单向运输。在有阀工作状态，半柔性阀形变最大，半柔性阀和流道由于加工和配合需要形成一定间隙，会引起流体的损失，在计算过程中对此进行忽略，根据伯努利方程

(19)

其中：H1=H2。

(20)

其中：ρ为流体密度；p1和p2分别为压电泵内部压力泵出水口压力；v1和v2分别为泵腔内流体速度和出水口流体速度；H1和H2分别为泵腔内流体高度和泵出水口处液面高度；A1和A2分别为半柔性阀安装处流道截面积和泵出水口截面积；f为压电振子驱动频率；ΔV为在1/4周期内腔体积变化量。

对圆形压电振子在某一驱动条件下，其振型曲面类似于半径为R的旋转抛物面。最大振幅位于振子中心，幅值为ω0，在压电振子上建立极坐标系，压电振子中心为坐标原点，极轴沿半径方向，纵坐标轴沿压电振子振动方向，则压电振子运动到最大振幅位置时，其方程为

ω(r)=ω0(1-r2/R2)

(21)

得到在1/4周期内，压电振子由于发生形变而引起泵腔内容积的变化量为

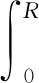
(22)

4 半柔性阀压电泵实验

图7为压电泵样机，泵盖和泵体采用有机玻璃制作，复合型压电振子基体用黄铜制作，并与压电陶

图7 压电泵样机Fig.7 Piezoelectric pump prototype

瓷黏接而成，压电振子与泵腔通过硅胶垫片与硅橡胶连接形成弹性支撑。表1为压电振子几何参数。

表1 压电振子几何参数

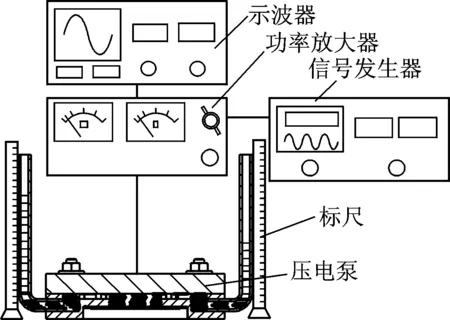
图8 压电泵压差实验示意图Fig.8 Schematic diagram of differential pressure test for piezoelectric pump

图9 压电泵实际压差实验测试Fig.9 Actual pressure difference test of piezoelectric pump

针对半柔性阀压电泵的性能，对泵样机进行压差和流量实验，实验采用纯净水作为工作介质。图8为压电泵压差实验示意图。图9为压电泵实际压差实验示意图，通过测试二次液面高度差Δh，反映压差大小。图10为泵流量实验示意图。压差测试时，为了方便观察，在水中滴入红色染料。泵出的水进入烧杯中，用电子秤取量烧杯中的单位时间内的流体质量。

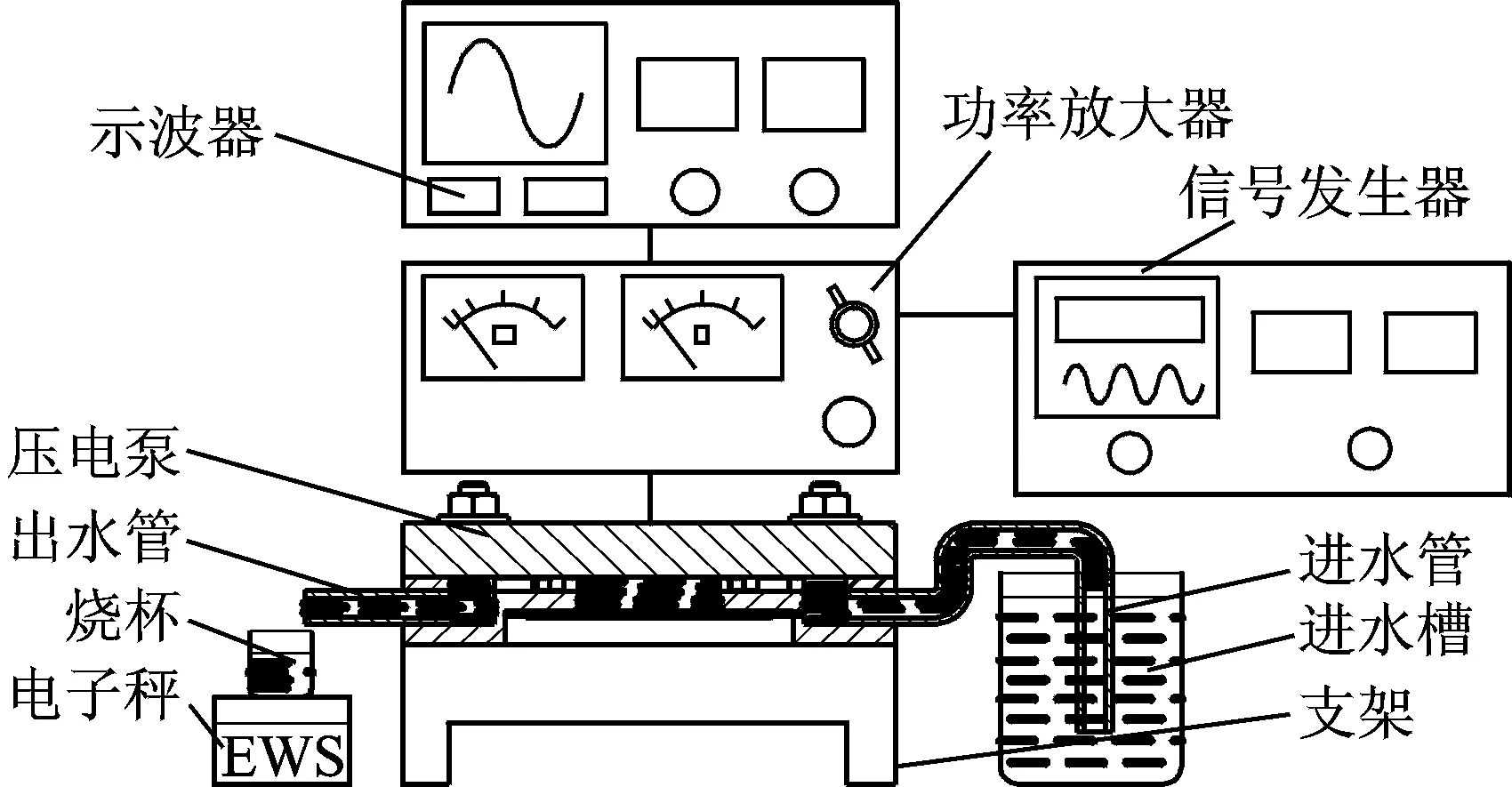
图10 压电泵流量实验示意图Fig.10 Schematic diagram of flow test for piezoelectric pump

5 实验结果及分析

实验时对压电振子施加不同电压和频率的交流电，得到压电泵频率与压差的关系如图11所示。驱动电压在40～140 V时，最佳频率为16 Hz，在16 Hz以下随着频率增加，压差也增加，在16 Hz以上随着频率的增加，压差下降。在电压为140 V、频率为16 Hz时，压差最大为51 mm；在电压为160～220 V时，最佳频率为7 Hz，在7 Hz以下随着频率增加压差呈上升趋势，在7 Hz以上随着频率增加压差呈下降趋势。在驱动电压为220 V、频率为16 Hz时，两端压差值为199 mm。由于泵阀跟从的缺陷[12]，压差随着频率增大而减小，直至接近于零。

图11 压电泵频率与压差的关系Fig.11 Relationship between piezoelectric pump frequency and pressure difference

图12 为压电泵电压与压差的关系。根据实验得到，当驱动电压在80～220 V之间，压差与电压呈正相关，电压上升，压差也逐渐增加，但不同电压范围最佳工作频率不一样。

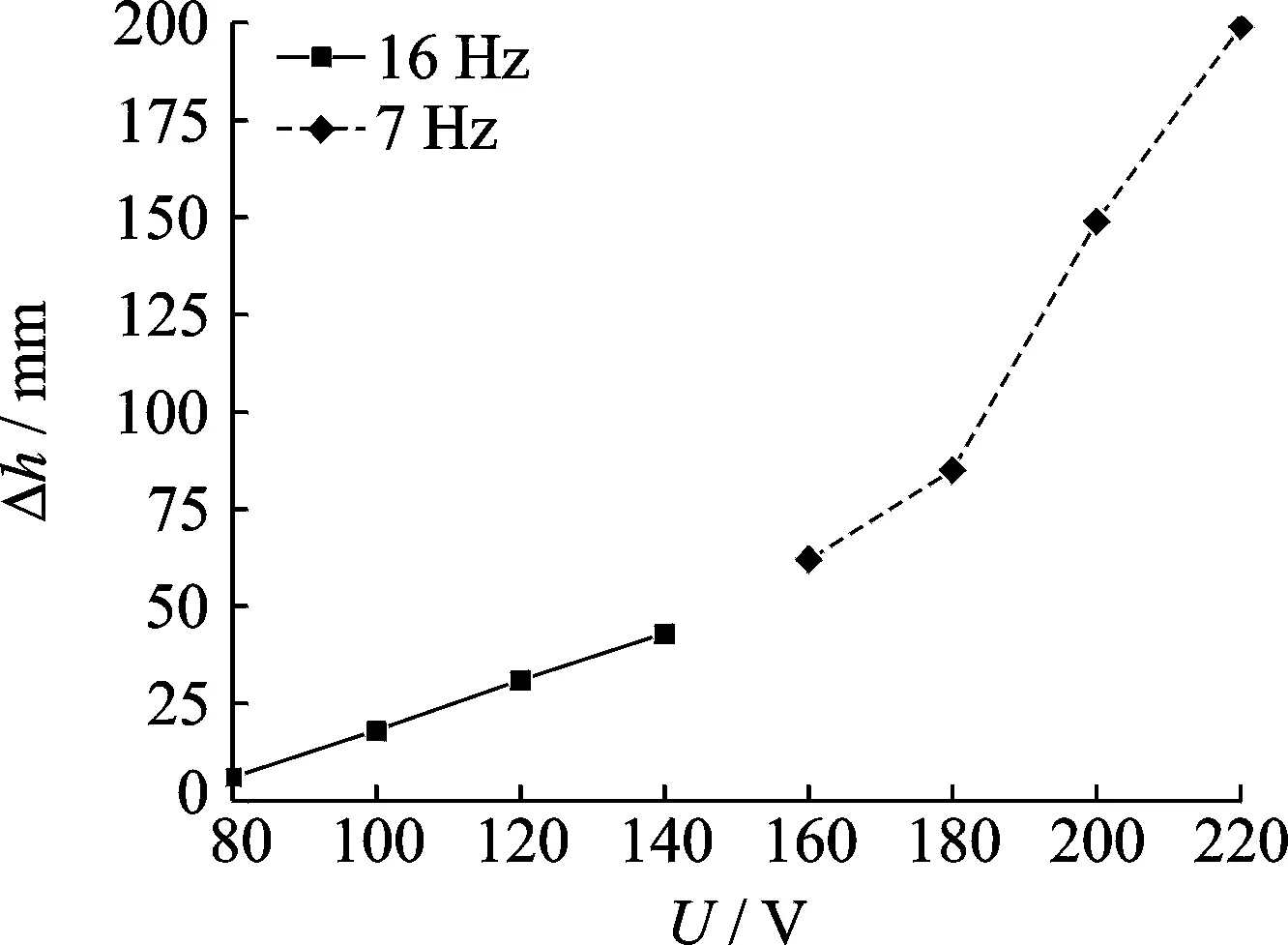
图12 压电泵电压与压差的关系Fig.12 Relationship between voltage and differential pressure of piezoelectric pump

图13为压电泵频率与流量的关系。根据实验可知，驱动电压在40～140 V时，泵频率与流量呈单峰变化，在22 Hz以下，随着频率增加流量也增加，随着22 Hz以上频率的增加，流量逐渐下降。在电压为160～220 V时，泵频率与流量为双峰变化，前一个峰值会随着电压增加逐渐高于后一个峰值，且后一个峰值对应的频率会随电压的增加逐渐变小。当电压增加，压电泵有效工作频率范围会逐渐加大。在出现双峰时，泵的最佳工作频率为22 Hz，随着电压增加，最佳工作频率为11 Hz。这主要是由于11 Hz为有阀状态，22 Hz为无阀状态，且随着电压增大，有阀状态效果大于无阀状态的效果。

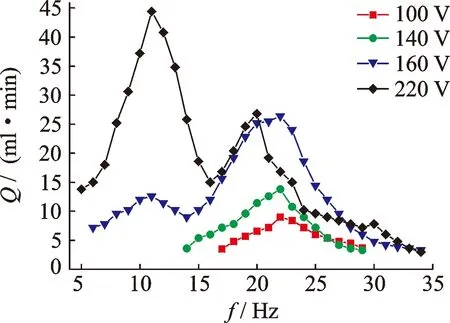
图13 压电泵频率与流量的关系Fig.13 Relationship between frequency and flow of piezoelectric pump

图14为电压与流量的关系。根据实验得到，驱动电压范围在40 ～280 V之间，泵流量随电压值升高而增加，但在22 Hz，200 V以后，电压与泵流量不呈正相关，主要原因是由于200 V以后，后一个单峰值对应的最佳频率会变小。

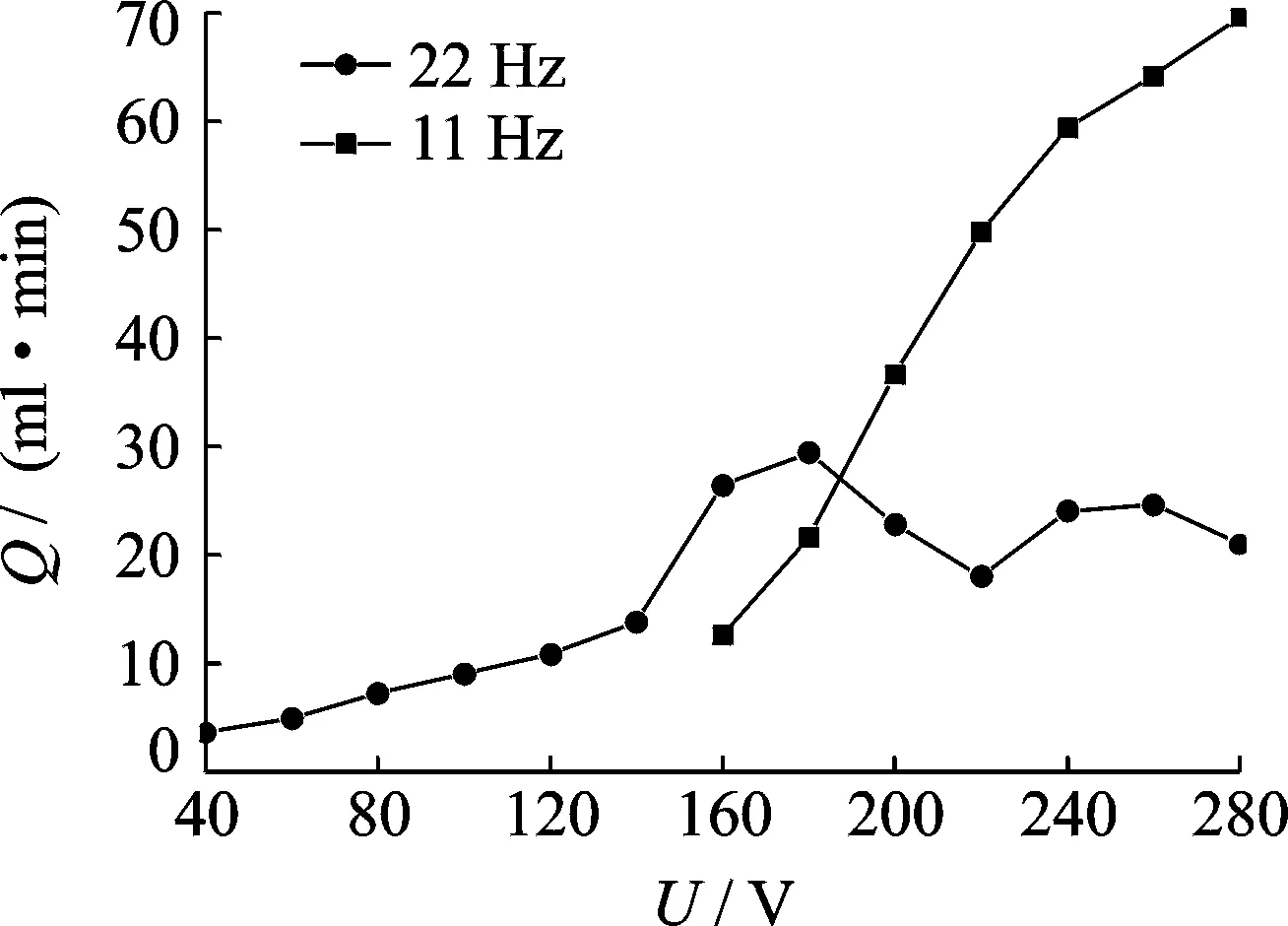
图14 压电泵电压与流量的关系Fig.14 Relationship between voltage and flow of piezoelectric pump

6 结 论

1) 笔者设计了一种新型结构的半柔性阀压电泵，该泵的关键部件是一种类静脉瓣结构阀，它属于材料为刚性，结构上呈现柔性的阀，可以在不改变其他条件时，实现两种工作状态，并实现流体的运输。

2) 对半柔性阀压电泵工作原理进行分析并建立伪刚体简化模型，分析了该模型对载荷的响应。得出泵腔内压力变化有利于阀体的功能的实现，从理论上验证了该泵功能上可实现状态的转变。

3) 对半柔性阀压电泵样机进行实验，测量了频率和电压幅值对压电泵压差的关系。实验结果表明：电压为40～140 V时，最佳频率为16 Hz；电压为160～220 V时, 最佳频率为7 Hz；在电压为220 V、频率为7 Hz时，最大压差达到199 mm；在特定频率下，进/出口压差随电压幅值的升高而增大。又测量了频率和电压值对压电泵流量的关系。实验结果表明：电压为40～140 V，流量随频率变化仅出现单峰，电压为160～220 V，流量随频率变化出现了双峰的变化，并对这一现象进行了解释。

4) 实验发现：在一定电压时，随频率变化，流量出现单峰；超过一定电压值时，随频率变化，流量出现双峰的现象并对这一现象进行了解释。