超声电机用开槽碟簧的计算与设计方法*
2019-11-06冷维杰孙志峻彭瀚旻
冷维杰, 孙志峻, 彭瀚旻
(南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
引 言
超声电机作为一门多学科结合的新技术,其工作原理是利用压电陶瓷的逆压电效应和超声振动来激发弹性体(定子)在超声频段内的微幅振动,并通过定、转子(动子)之间的摩擦作用将振动转换成转子的直线或者旋转运动,输出功率,驱动负载[1]。超声电机运行过程中,定子和转子之间的预压力对其摩擦性能有着重要影响,甚至直接决定了超声电机的整体输出性能,因此,对定子和转子施加稳定的预压力十分重要[2]。
开槽碟簧作为一种具有非线性刚度特性的承压结构,非常适用于超声电机的预压力加载。目前,部分超声电机已经采用碟形弹簧进行定转子之间的预压力加载,但是对于小尺寸系列超声电机,由于其尺寸的限制,需要对碟形弹簧进行结构改进设计。同时,由于小尺寸系列超声电机的输出性能对预压力的波动非常敏感,碟形弹簧的设计对计算模型的精度提出了更高的要求。目前,在碟形弹簧的设计过程中[3-5],普遍使用的传统计算公式是从经典的Almen-Laszlo 理论[6]出发,结合传统的悬臂梁小变形理论,推导出的载荷-位移刚度特性的计算公式(简称Schremmer公式[7])。但是该计算公式精度较差,适用范围受到诸多限制,不能满足设计需求。考虑到以上因素,笔者采用在碟形弹簧基础上进一步改进结构的开槽碟簧作为小尺寸系列超声电机的预压力加载部件,并基于圆锥壳体理论建立了开槽碟簧的力学计算模型。试验结果表明,该力学计算模型具有较高的准确性。
1 开槽碟簧的力学模型
1.1 开槽碟簧的结构
开槽碟簧的几何结构以及截面受压变形示意图如图1、图2所示。开槽碟簧可以看成由外圈的普通碟簧和内圈的数个分离齿组成。通过滑动简支条件的支承,开槽碟簧承受竖直方向上的轴对称载荷P作用。
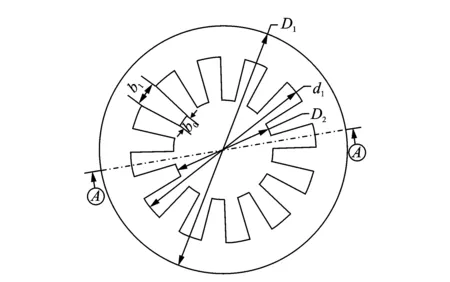
图1 开槽碟簧的基本几何结构Fig.1 Basic geometry of slotted belleville spring
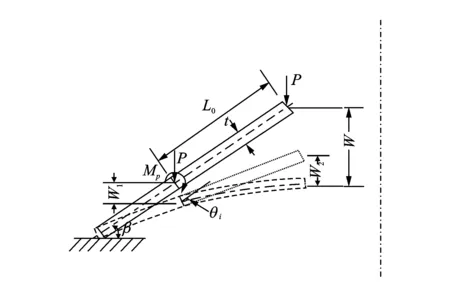
图2 开槽碟簧A-A剖面受压变形图Fig.2 Deformation image of A-A profile
1.2 外圈普通碟簧的力学计算模型
取外圈碟簧的一段变形微元进行分析,如图3所示。其中:左边表示未变形时候的状态;右边表示变形后的状态,变形后相应的变量用*号进行了标记;α为变形前微元沿径向的切线与对称轴的夹角;θ=α*-α为半径R处微元径向切线的转角;ξ为圆周方向;η为径向方向。
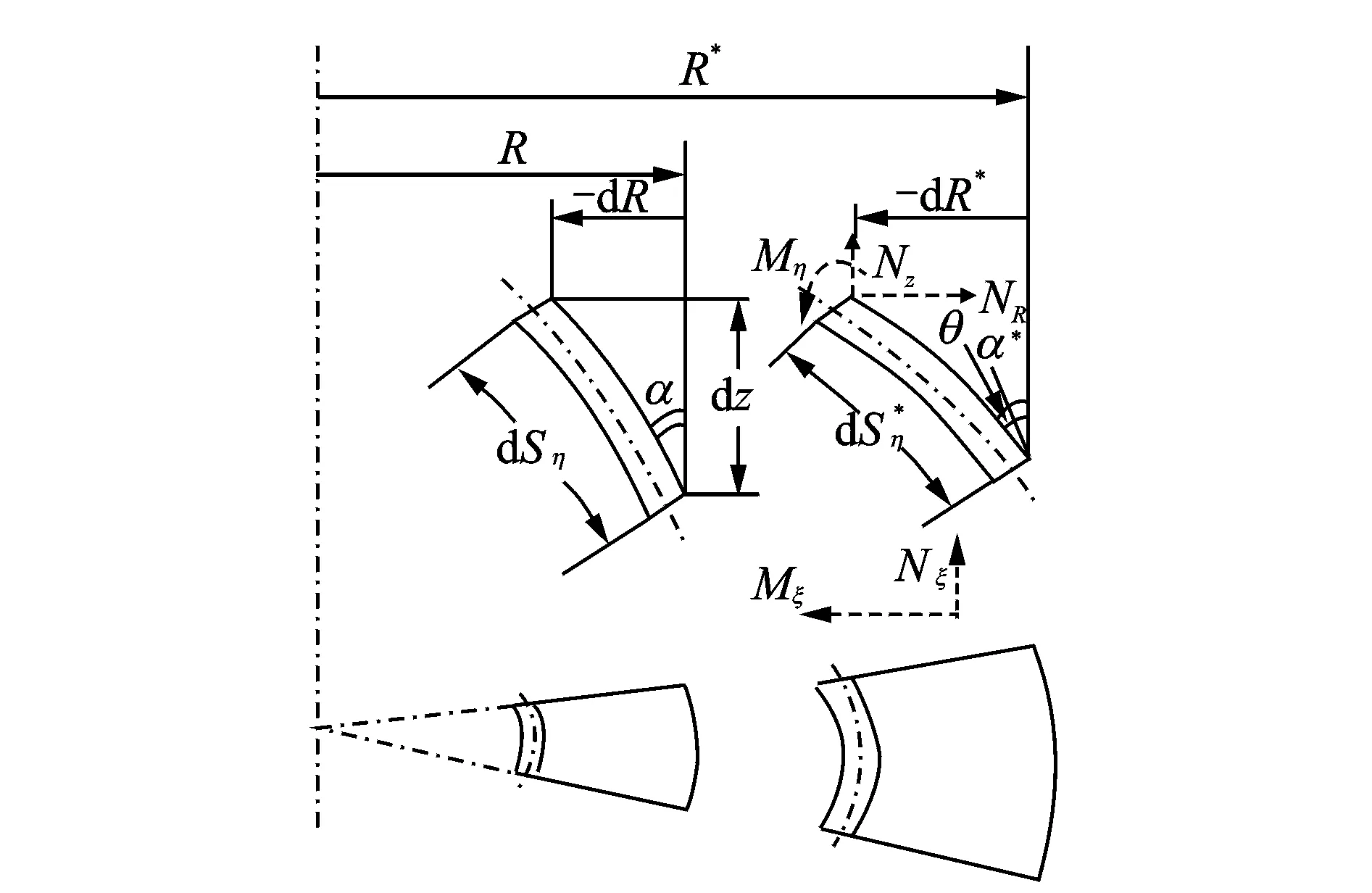
图3 径向微元的几何结构变形Fig.3 Structure deformation of radial infinitesimal
由几何关系可知,周向曲率的变化量xξ为
(1)
径向方向上,由于初始状态下,碟簧的曲率为零,因此径向方向上的中面曲率就是曲率变化量,径向曲率变化为
(2)
周向线应变为
(3)
径向位移为
ur=Rεξ=R*-R
(4)
径向方向上,中面线应变为
(5)
对式(4)微分并结合式(5)可得协调性条件
(6)
在竖直方向上, 微元在z方向的高度增量为
(7)
定义NR,Nz,Mx和Mh为微元中面单位长度上受到的力和力矩。考虑到几何结构和受力的轴对称性,微元所受的剪切力、扭矩以及横向剪切力Qx均为0,微元的受力情况如图4所示。
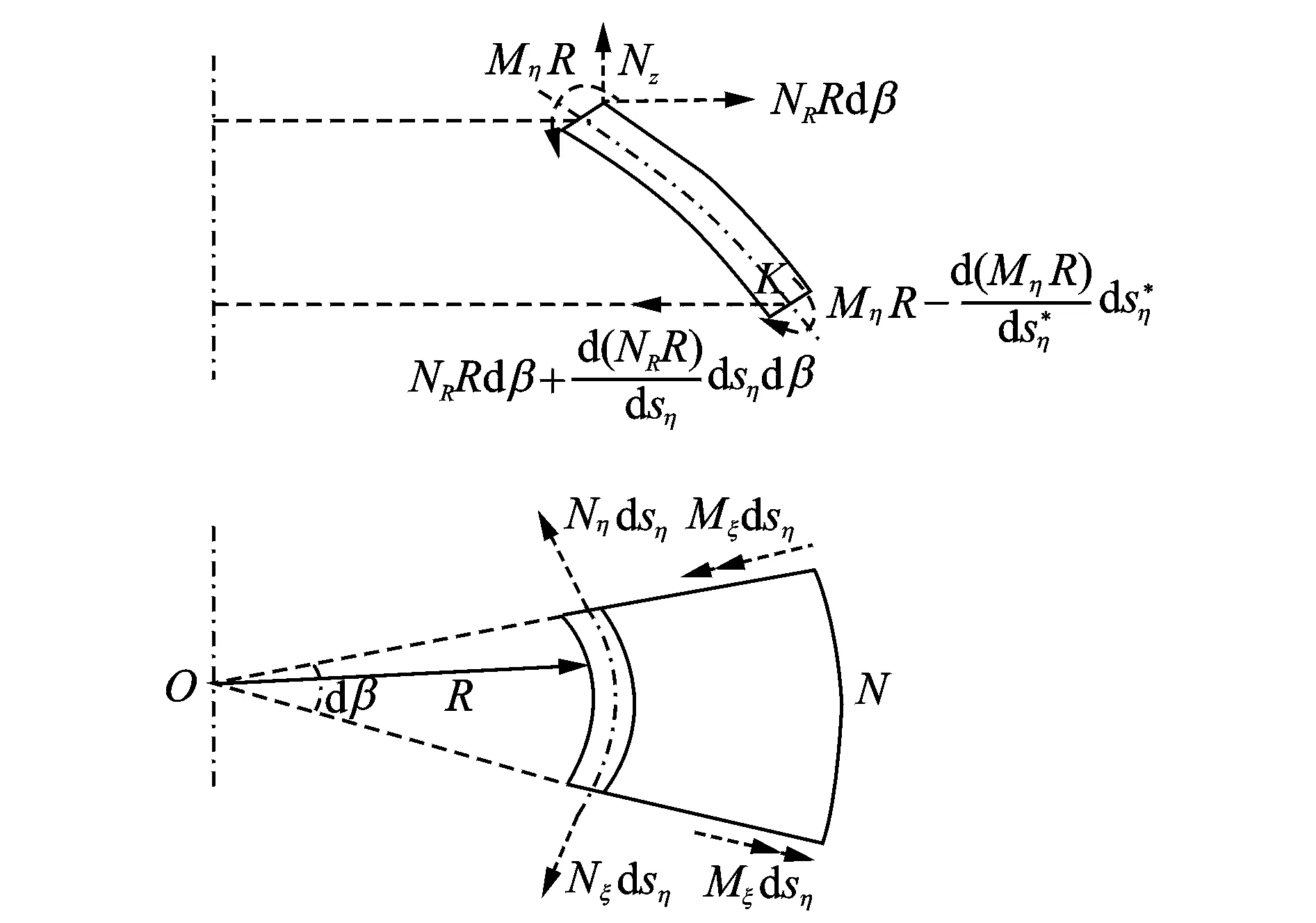
图4 微元受力示意图Fig.4 Free-body diagram of radial infinitesimal
记微分算子
(8)
其中:f为可微函数。
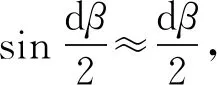
Nξ=-[V]′sinα
(9)
其中:V=NRR。
如图4所示,对K点取弯矩平衡有∑Mk=0,即有
(10)
沿径向方向的合力为
(11)
根据Kirchhoff-Love假设,可得圆锥壳的弹性定律为
(12)
其中:E为圆锥壳的弹性模量;v为泊松比;D=Eh3/[12(1-v2)]为弯曲刚度;h为圆锥壳的厚度。
将式(9)、式(11)代入式(12),并结合式(6)可得
(13)
将式(1)、式(2)代入式(12),并结合式(10)可得
(14)
碟簧的力学计算模型包含2个2阶微分方程式(13)和式(14),为了便于计算,先将上述2阶微分方程转化为只包含1阶变量的状态方程,并引入待求微元变形后的竖直位置变量z*和变形后的径向位置变量R*,得到以下包含变量组(θ,Rθ′,V,RV′,z*,R*)的状态方程组
(15)
求解上述方程组,即可得到碟簧在载荷P下的内径处竖直方向上的位移
(16)
由于开槽碟簧外圈碟簧部分的边界条件分布在内外径处,方程组(15)的求解问题为边值问题,采用打靶法将其处理为初值问题,并结合Runge-Kutta方法可进行求解。
1.3 内圈分离齿的力学计算模型
开槽碟簧的受载过程中,受竖直方向上集中力作用的内圈分离齿变形,可看作渐变截面悬臂梁自由端受集中载荷大变形问题进行求解,如图5所示。
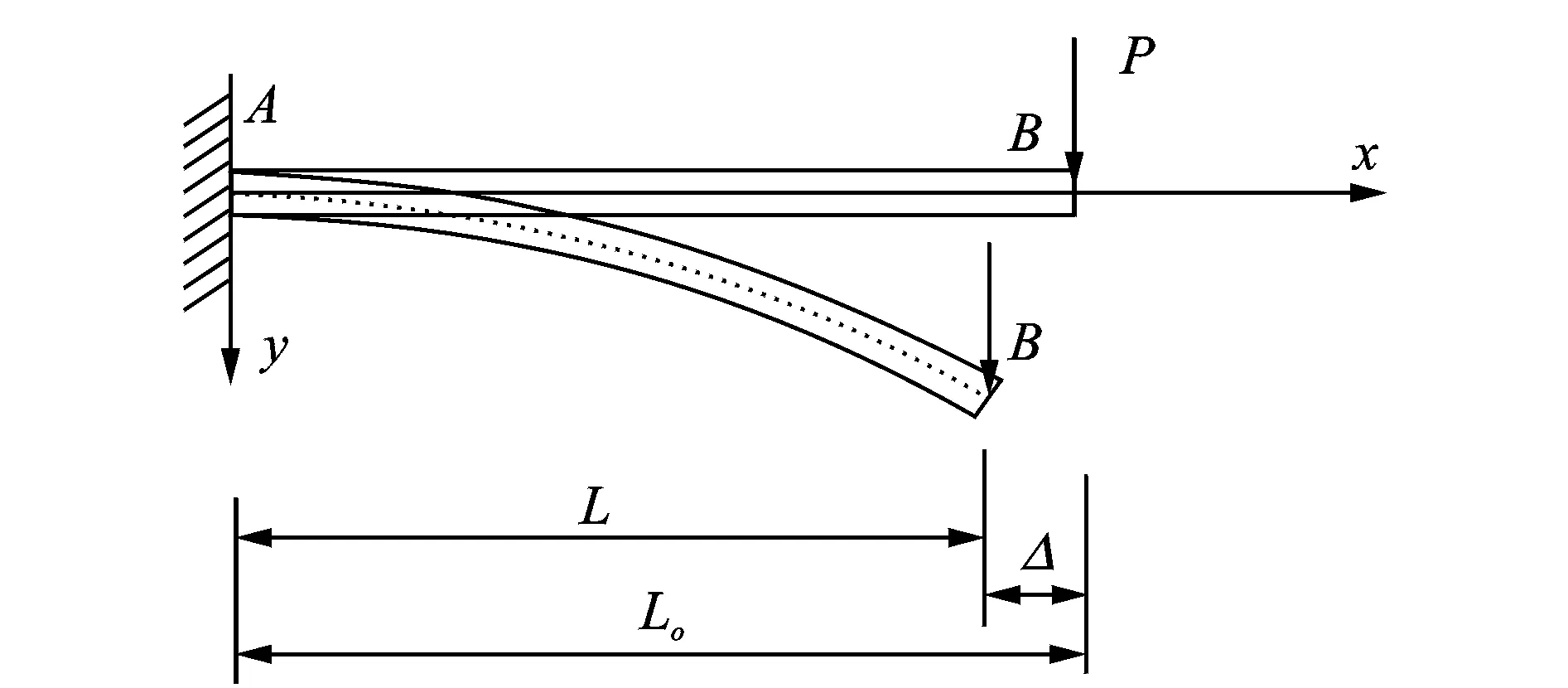
图5 悬臂梁自由端受集中载荷作用图Fig.5 Loading diagram of cantilever beam with concentrated load on the free end
目前,对于悬臂梁大变形问题,针对不同的受力情况和边界条件,已经得到了有效的计算方法[8-10]。由材料力学推导[11]可以得到任意情况弯曲变形的挠曲线微分方程
(17)
其中:w为x处悬臂梁的挠度;M(x)为x处悬臂梁所受到的转矩;I(x)为x处悬臂梁的截面惯性矩。
设定Q(x)=M(x)/I(x),y(x)=dw/dx,原曲线微分方程(1)可变换为
(18)
分离变量并积分可得
(19)
其中
(20)
从式(20)中解出y(x)并积分可得悬臂梁挠度
(21)
由于悬臂梁固定端处不发生移动和转动,因此该处的边界条件为
(22)
w|x=0=0
(23)
代入式(21)中可得积分常数C1=0,C2=0。
假设悬臂梁的原长为L0,受载变形后自由端水平位移为Δ,受载变形后的悬臂梁在水平方向上的投影长度为L,则有L=L0-Δ,如图5所示。由于变形前后悬臂梁的总长度保持不变,因此有条件
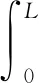
即
(24)
由以上推导可知,一旦确定了自由端的水平位移Δ,就可求得g(x)。水平位移Δ可以通过试误法确定,即先给定Δ某个初值,然后用二分法,当式(24)右边表达式的计算结果与悬臂梁原长L0的误差在设定的误差范围内时,可视作Δ即为所求。得到g(x)即可通过式(21)求得悬臂梁变形的挠度曲线。对于渐变截面悬臂梁,其基本几何结构如图6所示。其中:b1为齿根宽度;b0为齿顶宽度;b(x)为距离固定端x处的截面宽度。
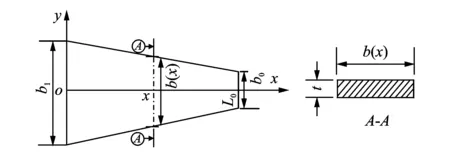
图6 渐变截面悬臂梁的基本几何结构Fig.6 Basic geometry of cantilever beam with gradual change section
由几何关系可知
b(x)=(1-x/L0)b1+(x/L0)b2
(25)
截面惯性矩I(x)为
I(x)=b(x)h3/12=b1h3/12+h3x(b2-b1)/12L0
(26)
将上述推导的b(x),I(x)代入式(20)可得
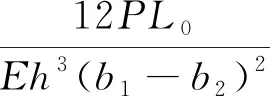
(27)
将g(x)代入式(24),利用二分法确定悬臂梁自由端水平位移Δ,然后重新代入式(27)求得g(x),最后通过式(21)求得悬臂梁变形的挠曲线方程。
1.4 开槽碟簧的力学计算模型
分离齿齿顶处的竖直方向上总位移由两部分组成:a.外圈蝶形弹簧变形带动分离齿的刚性转动;b.内圈分离齿的受载弯曲变形。
1.4.1 外圈碟簧部分
通过载荷移置,将作用在悬臂梁自由端的载荷P移置到外圈碟簧的顶部,其大小不变,并设定其均匀作用在整个圆周上,则作用在碟簧顶部圆周的线载荷大小为Pl=P/(πd1)。另外,由于载荷的移置,产生的移置弯矩Ml也作用在碟簧顶部圆周处,周向的线弯矩大小为Ml=Mp/(πd1),其方向如图2所示。开槽碟簧工作过程中,碟簧外径自由端水平方向受力NR为零,并且没有弯矩作用,即碟簧外径有边界条件
(28)
将式(9)、式(11)代入式(12),并结合式(4)可得外圈碟簧受载变形后的外径位置
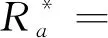
(29)
同时,碟簧外径处竖直方向位移为零,即
(30)
碟簧内径处,由于移置弯矩Ml的影响,其边界条件为
(31)
即
(32)
由于外圈碟簧在受载过程中产生了弯曲变形,计算外圈碟簧变形对开槽碟簧分离齿自由端总位移的作用大小时,应该考虑外圈碟簧顶端处的内锥角度变化的影响。设定碟簧顶端处的内锥角度变化量为θi,其具体数值可由1.2节求解碟簧刚度特性计算微分方程组中的变量θ得到,顶端处的内锥角度为βi=β-θi,则由图2中的几何关系可知,外圈碟簧受载变形对总位移的作用大小为
(33)
1.4.2 内圈分离齿部分
开槽碟簧的分离齿部分可以当做渐变截面悬臂梁进行计算,在1.3节中已经推导了渐变截面悬臂梁的计算模型。注意到开槽碟簧的几何结构特点,m个分离齿共同承载外部载荷P,因此对于单个分离齿,所受到的载荷Pi=P/m。由开槽碟簧的内锥角度β,可得外部载荷P在垂直于悬臂梁的y方向上的分力为Pv=Picosβ,可知距离分离齿齿根x距离处截面的弯矩为
M(x)=Pv(L-x)
(34)
其中:L=L0-Δ,Δ为悬臂梁自由端在x方向上的位移。
将式(34)代入式(27)可得
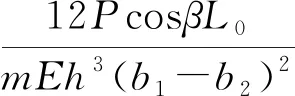
(35)
进一步将式(35)代入式(24),并通过试误法可计算得悬臂梁自由端的x方向上的位移Δ,然后通过式(21)
(36)
可求得悬臂梁自由端沿y轴方向的位移w,根据所求结果可得悬臂梁自由端在竖直方向上的位移为
W2=wcosθ+Δsinθ
(37)
由以上分析可得,开槽碟簧在外载P作用下的总位移大小为
W=Wi+W2=W1+W2+L0sinβ-
(38)
2 开槽碟簧力学模型的计算
选取试验开槽碟簧的基本结构参数如表1所示。
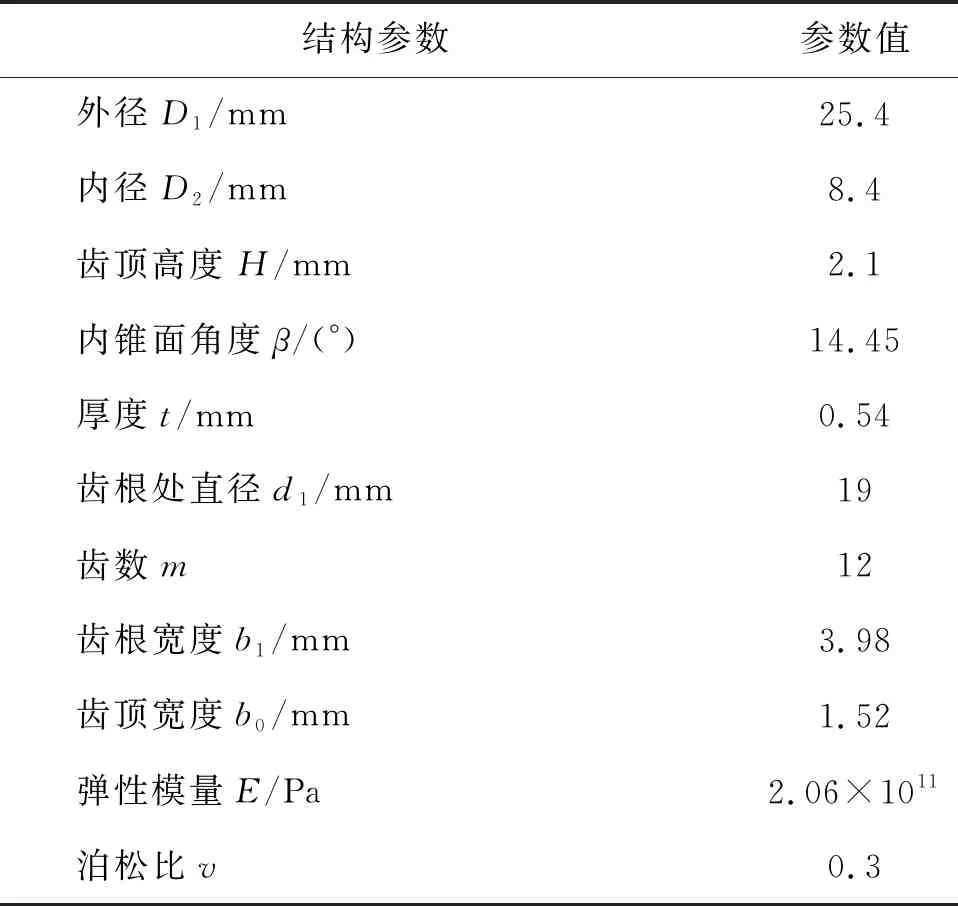
表1 开槽碟簧的结构参数
将本研究的计算结果与有限元计算结果、传统Schremmer公式结果以及试验结果进行对比分析,如图7所示。
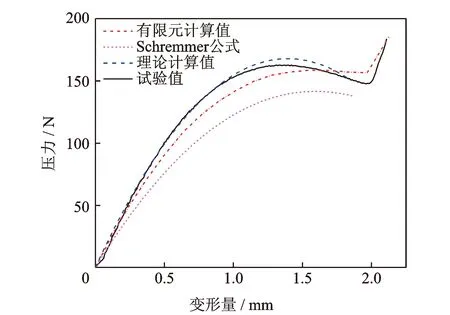
图7 开槽碟簧载荷-位移曲线对比Fig.7 Comparison of force-displacement curves
由对比结果可知,笔者提出的理论方法比传统的Schremmer公式以及有限元方法更加准确。相对于试验值,各个计算方法的相对误差如下:同一变形量情况下,Schremmer公式计算结果的最大相对误差达到了±23%,平均相对误差达到±18%;有限元方法计算结果的最大相对误差为±9.3%,平均相对误差为±5.8%;理论计算方法结果的最大相对误差仅为±3.5%,平均相对误差仅为±1.7%。在小变形阶段(变形量在0~0.7 mm之间),开槽碟簧的载荷-位移刚度特性近似呈线性关系,该线性段的压力值范围可达0~127 N。变形量在0.7~1.39 mm范围时,开槽碟簧的刚度逐渐较小,在变形量WP=1.393 mm时,刚度变为零,并达到受载的最大值Pmax=168 N。当变形量大于Wp,开槽碟簧特性曲线处于负刚度阶段。另外,有限元方法的计算值与试验值在曲线的末端均有一个压力值随位移迅速增大的上翘阶段,而笔者提出的计算方法得到的曲线没有上翘阶段。主要原因在于开槽碟簧试验和有限元模拟过程中,在曲线末端处已经处于压平状态,上下压板开始挤压开槽碟簧,此时压力随着变形的增加而迅速增大。但是对于理论计算方法,由于压力与边界条件始终限定在内外径处,开槽碟簧被压平之后还可以继续沿受载方向发生变形,因此不会出现压力值随位移迅速增大的上翘阶段。
3 准零刚度特性的参数敏感性分析
3.1 参数敏感性试验流程
为了满足超声电机对开槽碟簧准零刚度特性的需求,建立基于准零刚度特性需求的开槽碟簧结构设计方法,需要分析准零刚度特性对开槽碟簧的结构参数的敏感性。
在实际超声电机用碟簧的制作过程中,考虑到制作工艺和原材料成本,一般选用弹簧钢进行开槽碟簧的设计制作,因此,其基本的材料属性(如弹性模量E和泊松比v)已经确定,本研究主要对开槽碟簧的几何结构参数进行设计。另外,由于小尺寸系列超声电机的尺寸限制以及开槽碟簧的装配限制,开槽碟簧的外径D1一般根据实际情况设定。因此,对于超声电机用开槽碟簧的结构参数设计,设计参数组包含的结构参数为
(d1,D2,t,H,c)
笔者基于Matlab编制的准零刚度计算程序,利用Isight数字化分析软件平台,建立了敏感性分析试验流程,如图8所示。
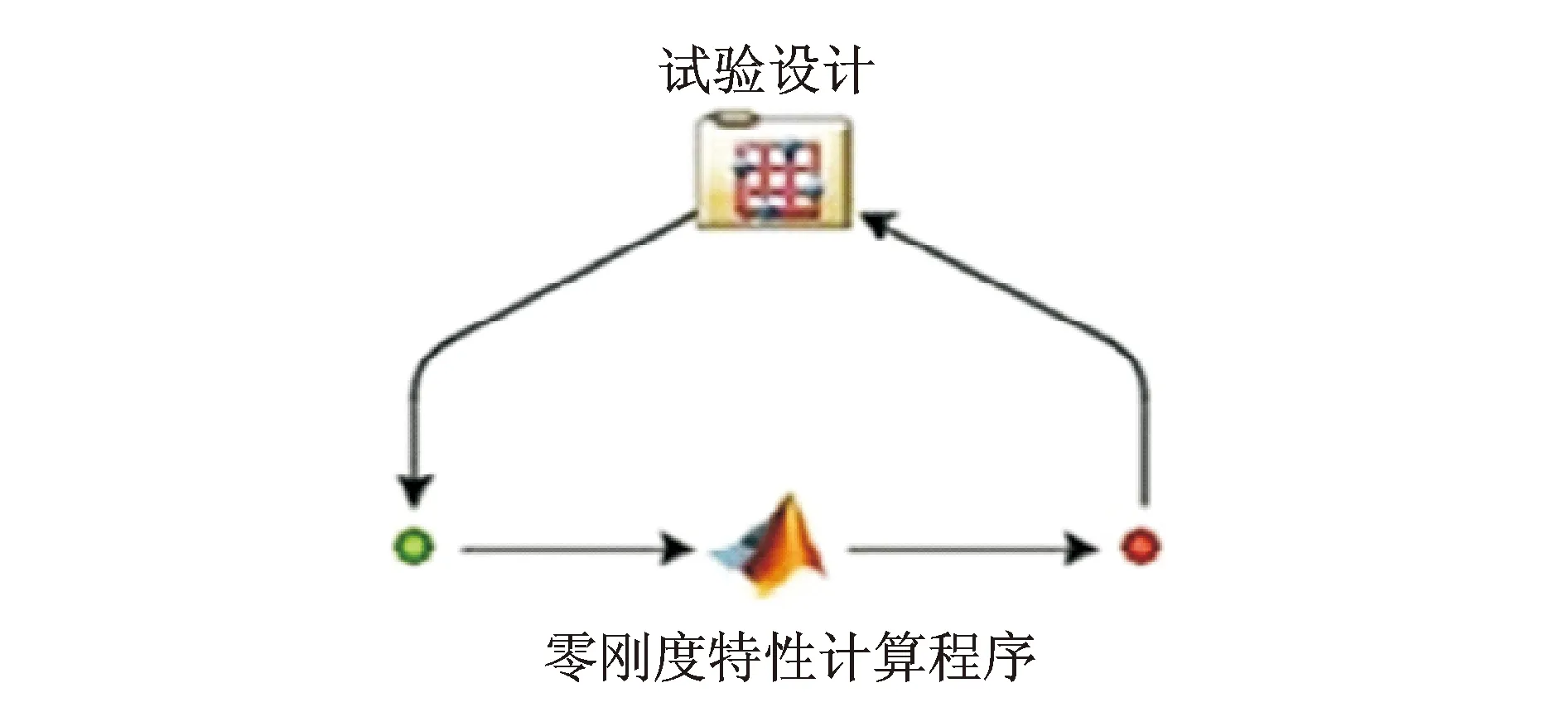
图8 敏感性分析试验流程Fig.8 Flow of parameter sensitivity analysis
试验过程中,试验模块首先将样本点传递给计算程序Matlab,计算得到结果之后,将结果由Matlab传递给试验模块。如此不断进行循环计算,直到试验方案中的样本点全部计算完成,试验结束。整个试验过程,样本点的选择对试验分析结果有很大的影响。因此,为了使样本点的选取更加容易,对设计参数组进行变量代换处理,设定
(39)
试验参数组变化为(q1,q2,q3,H,t),根据开槽碟簧的实际使用情况,参数组的约束范围为
(40)
在以上约束范围内,布置2 000个试验样本点,并进行均匀优化处理。设定参数组(q1,q2,q3,H1,t)为试验因子,准零刚度区间长度L(q1,q2,q3,H1,t)为试验响应。
3.2 试验结果分析
通过试验方案流程的计算,得到试验响应对试验因子的敏感性分析Pareto图,如图9所示。
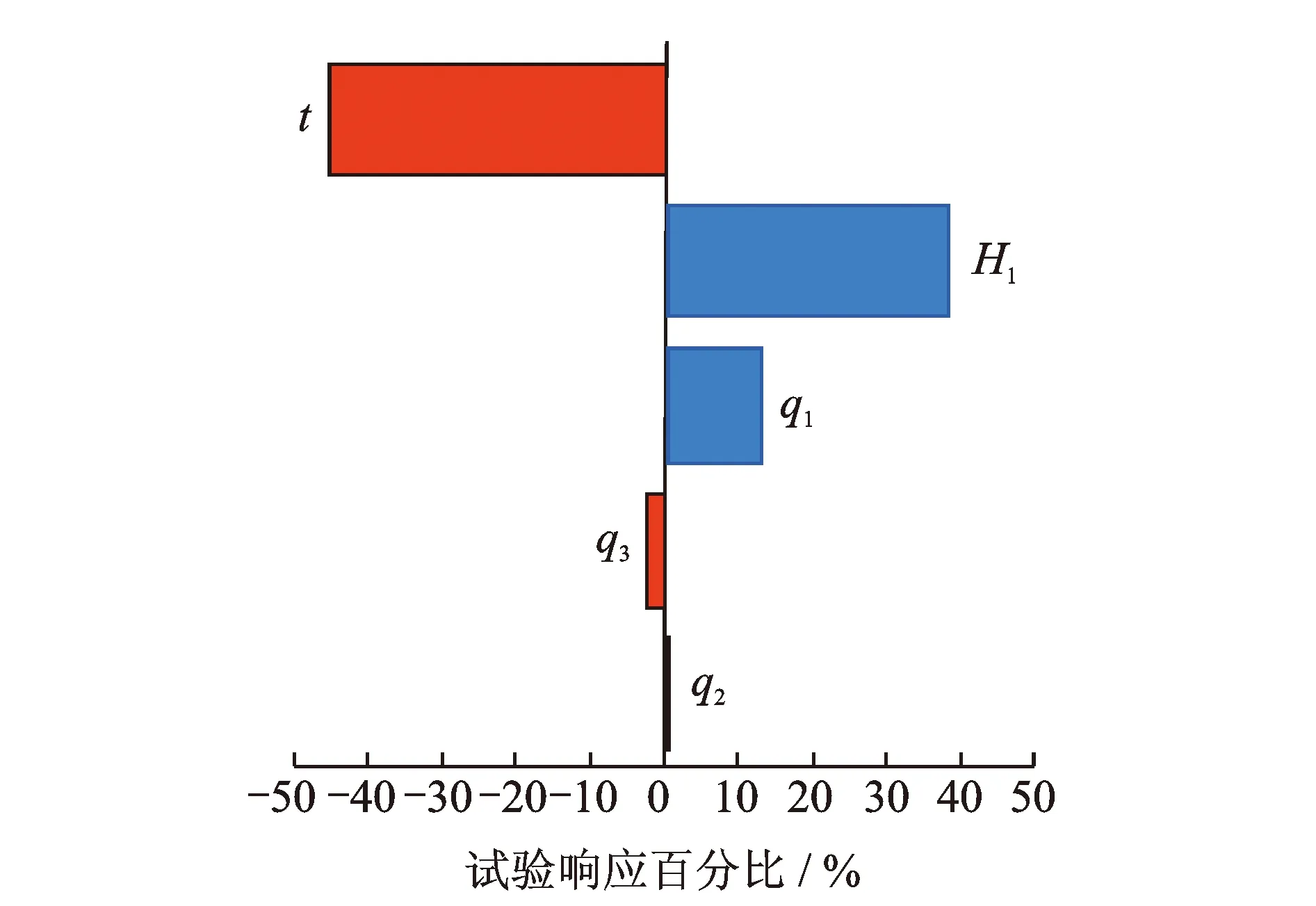
图9 试验响应的Pareto图Fig.9 Pareto diagram of test response
图9表示试验因子对试验响应的影响程度,并以百分比的形式按照影响程度的大小从上到下排列出来。其中:蓝色代表试验因子和试验响应呈正相关;红色代表试验因子和试验响应呈负相关。由图可以看出:开槽碟簧的厚度t与准零刚度段长度L整体呈负相关,并且相比于其他参数量,其影响程度最大,百分比超过了45%;外圈碟簧的自由高H1对准零刚度段长度L的影响程度百分比将近40%,二者整体呈正相关;其余参数量对准零刚度区间长度L影响不大。
从样本点计算结果中输出外圈碟簧自由高H1和开槽碟簧厚度t对准零刚度段长度L的三维结果图,如图10所示。
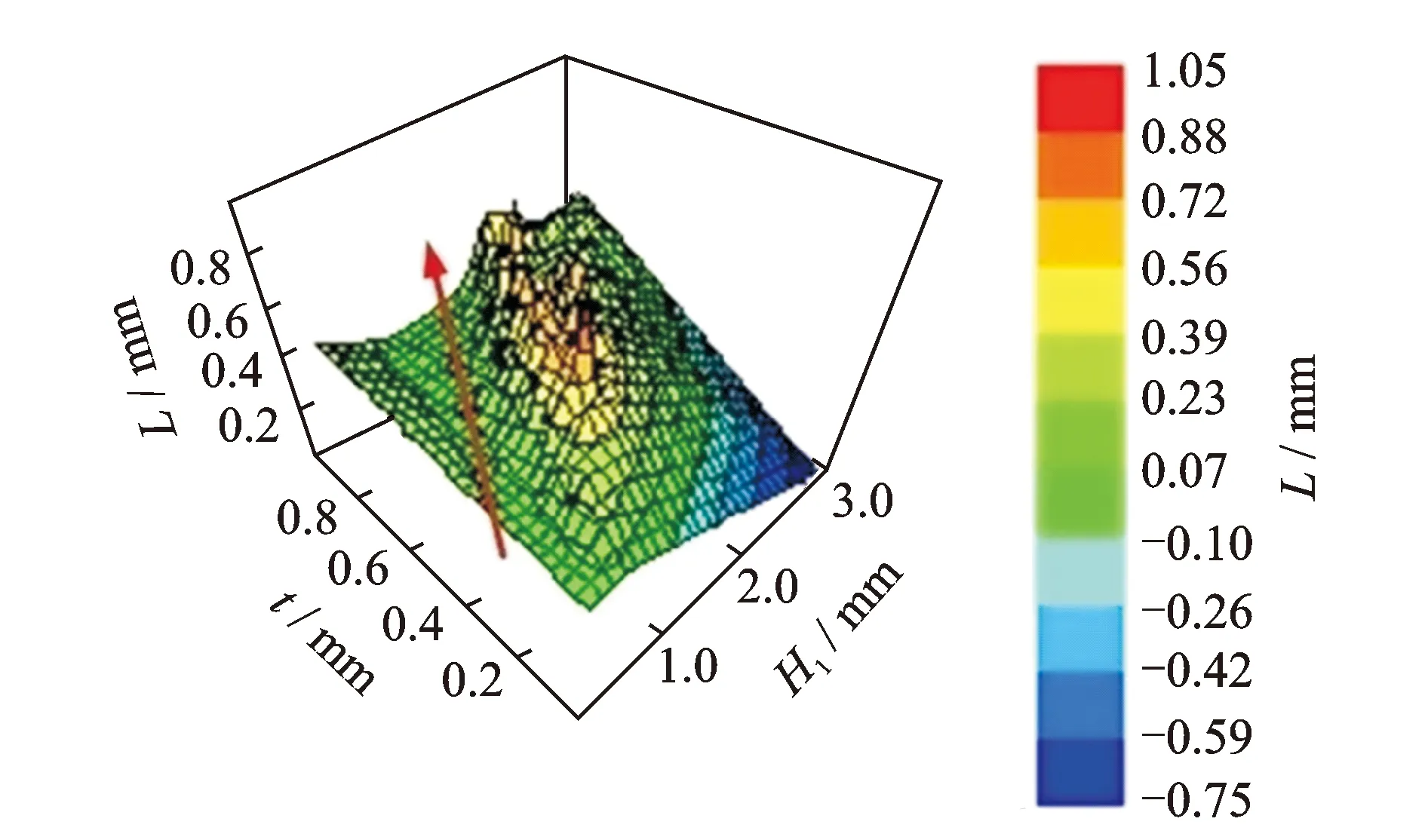
图10 高度H1和厚度t与长度L的关系图Fig.10 Relation graph of height H1, thickness t and length L
由图10可以看出,沿图中红色箭头方向,准零刚度段长度L的大小一直处于峰值附近,该方向是指向零刚度段长度影响的最优方向。因此,进一步考虑高厚比H1/t对准零刚度段长度L的影响情况。由计算结果输出高厚比H1/t与L的等值线图,如图11所示,其中H1/t为无量纲单位。
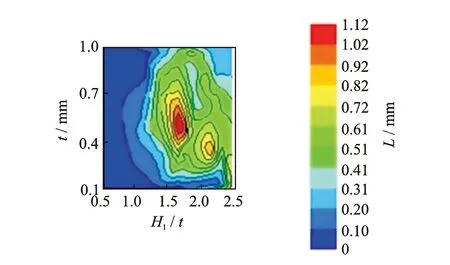
图11 高厚比H1/t与厚度t等值线图Fig.11 Contour plot of H1/t and thickness t
由图11可以看出,试验响应存在一个峰值区域,该区域对应的高厚比H1/t的最优取值范围为
1.5
(41)
由以上分析可知,在开槽碟簧的设计过程中,可以先设定开槽碟簧的高厚比最优取值范围,然后基于最优取值范围,对其他变量进行优化设计。
4 结 论
1) 基于圆锥壳体理论以及渐变截面悬臂梁大变形理论,建立了开槽碟簧在滑动简支条件下受轴向载荷的力学模型。对比分析结果表明,该力学模型比传统计算公式和有限元方法更加准确,相对误差在±3.5%以内。
2) 基于本研究提出的开槽碟簧准零刚度特性计算方法,设计了准零刚度特性的结构参数敏感性试验。由试验结果分析得到了准零刚度特性的最优高厚比取值范围为1.5~1.8之间,可作为准零刚度特性开槽碟簧结构的设计参考。
