借助几何直观，发展空间观念

谢华英

摘 要：文章分析了学生应如何借助几何直观，发展空间观念。教师应从抽象概念入手，帮助学生形成空间意识;动静结合，发展学生空间观念;培养学生养成画图的习惯，运用数形结合，促进空间观念的形成;操作和想象并行，充分感知，促进空间观念的深化;由直观到抽象，动静结合，促进空间观念的提升。

关键词：几何直观;空间观念;图形转换

《义务教育数学课程标准（2011年版）》指出，空间观念是学生在学习过程中通过几何学习和图形学习实现的目标，其目标包括分析、抽象、观察、综合、比较、想象的过程。融入几何和图形学习的整个过程，在图形认识、图形位置、图形运动中都蕴含着学生发展空间观念的任务。几何直观是数学素养的重要指标，借助几何直观可以把复杂的数学问题变得简明、形象。教师应该在教学过程中多创造机会，引导学生借助几何直观，发展学生空间观念，提高学生数学素养。

一、创造机会，形成空间意识

（一）从抽象概念入手，帮助学生理解概念

数学概念的理解，对学生空间观念的发展十分重要。教学时教师可以利用多种措施加深学生对概念的理解，学生先要进行直观认识，随后创建表象，再到抽象总结、理解事物本質，最终展开想象。在观察物体的过程中，需要先把初始形状和事物具体某一面有机联系起来，随后掌握形状的一般概念，再到不需要参考具体事物便可以辨别图形。在认识位置和方向的过程中，应该从实践性角度入手，辨认实际方向，随后进行想象，通过参照物来辨别具体位置，了解方向的相对性特征。在认识图形的过程中，应该是先对图形进行直观辨认，随后通过语言描述具体特征。在学习图形运动的过程中，应该从现实情境中感知图形运动变化。

例如，在“线”的学习过程中，教材给出了生活中的一种绷紧的常见弦和一个拽紧的线，指出可以将两者都看作是线段。将琴弦或线画到纸上便是线段，而线段的两端是线的端点，因为在日常生活中无法找出直线的原型，所以教材中提出将线段向两端进行无限延伸便可以得到直线。在教学过程中，教师可以引导学生思考无限延长的意义，想象直线到底多长，是否可以测量直线的长度。随后引出射线的概念，从生活中寻找射线的原型。最终在对图形中的线段、射线和直线进行认识后，可以思考其中的差异和相同点。

（二）从抽象概念入手，掌握图形变换

图形运动与几何变换是小学数学中的重点内容，是形成数学思维的基础方法和学习的主要对象。因此在教学过程中，学习平面图形时不仅要掌握标准图形，同时还需要了解转换方位后的图形。比如，在构建体积、面积公式的过程中，应该通过形状变化掌握哪些发生改变，而哪些没有变化，通过现有知识进行推导，并得出体积公式和面积公式，在遇到一些比较复杂的问题时，可以通过等积替换法、转化法、割补法、平移法等方法来实现图形的变换。

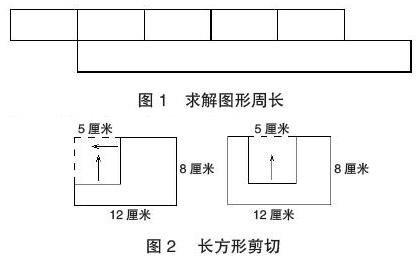
教师在练习设计中，应该适当添加各种图形变化方法习题，如两个相同的长方形，长是20厘米，宽是2厘米，将其中一个顺着长边平均分成五等分，随后将其拼接在一起，试问该图形的整体周长。具体如图1所示。

二、动静结合，发展空间观念

空间观念的培养需要以事物的想象和观察为基础，学生经过一段时间的学习已经具备了分析、想象和观察的基础。为此，在小学数学课堂教学过程中，教师可以结合学生所了解的现实问题，设置教学情境，引导学生利用自身经验进行观察、描述、分析、画图和想象，促使学生逐渐形成空间观念。

（一）养成画图的习惯，数形结合，促进空间观念的形成

数形结合是对相关技能和知识的贯通式理解，逐渐形成的一种数形之间的转化意识，这种运用能力和认识能力是教学过程中所需要的。为此，教师应该引导学生树立画图观念，将需要解决的问题图形化，使计算和问题更加直观，促进形象思维的有效展开。

比如，在“数对”教学中，教师可以引导学生将数对和方格纸中的点联系起来，并形成一种对应关系，用数对的形式来代表方格中的点，或是通过方格中的点来表示数对。在学习分数和小数的过程中，学生可以用直线中的刻度点设置对应关系，通过直线中的点显示数，或用数字来表示具体的点。在“正负数”学习内容中，可以在数轴中寻找对应点，用正负数表示两种意义相反的数量，掌握其中一点的正数便表示可以找到另一个负数点。

又如，从一个长为12厘米、宽为8厘米的长方形中，剪下一个正方形，而正方形的边长是5厘米，剩下的图形周长最长是多少厘米？这道题单纯通过想象很难解决问题，在这种状况下通过画图的方法，可以使整个计算过程更加简单。通过画图，学生可以很清楚地知道，第一种剪法，图形周长和原来相等，而第二种剪法，周长比原来增加了10厘米。具体如图2所示。

（二）操作和想象并行，充分感知，促进空间观念的深化

皮亚杰曾说：“空间观念的形成不像拍照，要想建立空间观念，必须有动手做的过程。”儿童的智慧集中在手指尖上，指尖上的数学如何更具智慧性，笔者认为想象与操作的相结合是一种行之有效的方法。这样既能避免表面化的操作，又能使操作活动更具数学化、思维化，更能在想象的过程中发展学生的空间观念。

例如，教学“长方体的认识”时，笔者为各小组准备了一些不同颜色的小棒和接口，让学生通过小组合作选取材料来搭一个长方体，在选材料的过程中，学生其实是在头脑中“搭”，接着再动手验证“搭”，这样既理解了长方体的基本特征，又初步建立起立体的三维表象，加深了对长方体的空间感知，空间观念得到发展。接着，笔者让学生想象：“如果把搭好的长方体拆掉1条棱，你还能想象出它的形状吗？想一想，最少剩下几条棱时，这个长方体的形状还是确定的？”

一开始减少1、2根棱的时候，对学生的空间想象力的要求比较低，学生很容易就能想象出来。当棱越来越少的时候，对空间想象力的要求也在逐渐增大，学生的空间想象能力实现了有层次性的培养、提升。当棱的数量减少到下面只剩长、宽的时候，大部分学生想象不出来了，有部分学生仍然可以想象出几种可能性：有可能垂直于底面的棱比较长，这个长方体比较高（课件显示比较高的长方体配合学生想象）;还有可能垂直于底面的棱比较短，这个长方体比较矮（课件演示）。

在师生、生生互动交流中，师生共同确定相交于一个顶点的三条棱可以确定长方体的形状、大小，从而揭示出“长、宽、高”的定义，接下来进行一系列的面、体的转换想象练习。借助三条棱这个中介，通过空间想象，在实际物体、几何图形与特征描述之间建立了可逆的联系，缩短了二维空间与三维空间的距离。

（三）由直观到抽象，动静结合，促进空间观念的提升

小学生的思维方式还处于从形象思维向抽象思维发展过渡的阶段，这就决定了其空间想象能力的培养必须从观察入手，动静结合。

在教学“探索图形”这课时，笔者充分运用多媒体技术，实现了对学生的空间想象能力有层次性的培养、提升。 课上，笔者出示用27小正方体拼成的表面涂色的大正方体，并有意把它打乱，顺势引出：“你们能帮老师还原这个大正方体吗？”这时的学生自信满满，认为只是小菜一碟。但是过了两分钟，大部分小组却无法还原，这引发了学生的思考，学生们就七嘴八舌地说开了，有的学生说：“这事看着简单，没想到做起来还挺难的。”有的学生说：“位置老放不对。”还有的学生说：“小正方体涂色情况有很多种，容易乱。”

这时，教师从中提取以下3个问题。

问题一：小正方体涂色的面有哪几种情况？

问题二：每种情况分别有多少块？

问题三：每种情况分别在什么位置上？

教师提问：“你们心中想的是这些问题吗？请你们认真观察手中的黄色正方体（不能拆开），并思考大屏幕上的问题，把你的想法以算式的形式表示出来。”

这时，热闹的课堂顿时安静下来了，学生通过几分钟的静静思考，很快得出答案。接着，教师通过多媒体课件的变色处理，让学生很直观地观察到每种正方体的位置规律：3面涂色的位置就在顶点上，2面涂色的小正方体在棱中，而1面涂色的就在面中，没有涂色的包在体中。

而在探索棱長为4厘米的正方体时，教师不再提供实物，而只提供平面图让学生在脑海中找出位置并算出各种情况的块数。当学生汇报答案时，对没涂色的正方体到底有几块产生了争议，此时教师利用课件的动态演示，把正方体一层一层拆解，让学生将看到的与自己刚才的想象进行对比，不断深化空间想象能力。对于棱长为5厘米、6厘米的正方体，教师则放手让学生通过想象、推理、探索得出答案，并引导学生观察，最终总结出规律。

通过触觉、运动觉与视觉的协同活动，动静结合，学生空间观念发展得到有力支撑，这个形不仅印在学生的眼中，还深深地刻在学生的脑中。

综上所述，学生空间观念的发展并不是一蹴而就的。学生生活经验越丰富，空间观念的形成就越快。无论是观察、画图、演示还是操作、想象，其核心都是借助几何直观，以便帮助学生循序渐进地逐步脱离具体的形象，从而走向几何的抽象;以提升学生数学思维，积累数学经验，促进其空间观念的形成。

参考文献：

[1]马增福.小学数学“空间观念”与“几何直观”中“核心素养”解读——以人教版小学数学为例[J].教育实践与研究，2018（9）：4-15.

[2]陈玲玲，柯爱武.借助几何直观 发展空间观念——“探索图形”教学实录与评析[J].小学数学教育，2017（19）：67-69.

[3]柏雨濛.关于“北师大版”初中数学教科书中“几何直观”的内容研究[D].沈阳：沈阳师范大学，2017.