舰载相控阵雷达组网资源管理的一致性算法

2019-11-05杨善超田康生吴长飞

兵工学报 2019年10期

杨善超，田康生，吴长飞

(空军预警学院预警情报系, 湖北武汉 430019)

0 引言

相控阵雷达(PAR)因为其波束快速捷变扫描能力、丰富的工作波形、强大的资源配置等优势，从技术上缓解了目标容量与数据率之间的矛盾，能够同时执行多种任务[1]。但是PAR体制在执行多种任务时也会受到自身时间和能量资源的限制，为了更好地应对各种威胁，在现代反导预警体系中PAR都会以组网协同的方式进行工作。为充分利用PAR网络(PARN)性能，必须实现高效的资源协同管理，即利用有限的资源，选择合适的雷达对合适的目标进行服务，进而完成对多扫描空间和多目标的探测跟踪任务[2]。

PARN资源管理属于传感器管理范畴，其结构分为集中式和分布式两种[3-4]。相比于集中式资源管理，分布式结构存在以下优点[5]：1)面对节点失效和网络攻击时有更强的鲁棒性；2)具有较好的可扩展性能，适应更多的雷达节点；3)能有效减少计算资源和信息传输资源的消耗。因此分布式资源管理是雷达界的研究热点之一。

文献[5]针对空间目标跟踪中的分布式传感器管理，提出了基于一致性的拍卖算法，其前提是任意雷达可以获得并利用全局信息。文献[6]研究了运用拍卖算法进行分布式传感器管理，以确保由通信代价引起的能量有效性问题。文献[7]针对无线传感器网络的目标跟踪问题，以信息增益为目标函数，提出了一种合作型分布式传感器分配算法。文献[8]研究了基于局部信息的分布式传感器管理方法，将整数规划问题松弛化，通过梯度法进行求解。文献[9]通过重新定义最小化低概率拦截(LPI)性能的目标函数，构建了基于LPI的分布式雷达网目标跟踪资源管理算法。这些算法致力于解决分布式多传感器多目标分配问题，在一定程度上提升了系统性能，但是研究前提条件都是任意传感器节点间可进行信息传输并获得全局信息，且不考虑噪声干扰。对于舰载PARN(SPARN)而言，各节点通过无线通信的方式进行信息传输，无法获得全局信息，并且信息传输会受到噪声干扰，造成各雷达对其他节点的资源状态信息等存在估计偏差，进而导致资源分配方案不一致的问题。

针对SPARN分布式资源管理，本文首先利用图论方法表示雷达网的拓扑结构，在此基础上提出基于一致性的资源管理算法。算法分两阶段：第1阶段是本地资源管理优化，构建出平衡各雷达负载且使资源消耗最少的资源管理优化模型，每个雷达根据该模型给出关于整个网络的本地雷达分配方案；第2阶段是分配方案一致化，根据网络拓扑结构进行各雷达节点间的信息传输，利用一致性算法对所有本地分配方案进行处理，得到全局一致性的分配方案。

1 预备知识和问题描述

1.1 PARN的图形化表示

PARN的拓扑结构具有多样性，不论哪种结构，都可以用图论的方法对其进行图形化表示。图的数学表示形式为G={Θ,Γ,A}。对于一个由N节点组成且节点间信息传输有方向限制的PARN，可以用一个有向图G来表示，其中，Θ={1,2,…,N}是N个雷达节点集合；Γ⊆N×N是有向边集合，如果i、j之间存在有向边即eij∈Γ，则表示雷达i可以传输信息给j；A=(aij)N×N为图G的加权邻接矩阵，如果eij∈Γ，则aij=1，否则aij=0.

在一个有向图中，如果任意2个节点之间都存在着一条有向路径，则称其为有向强连通图。对于所有雷达间都能相互传输信息的网络，可以用任意两节点间皆存在路径的无向图(无向图与有向图的构成要素相同，但边是没有方向的)G来表示，称为连通图[10]，在该图中，Γ要包含任意两节点之间的无向边。对于无线通信的SPARN，有向强连通图的拓扑结构更为常见。图1(a)为一个包含5个节点的PARN有向强连通图。

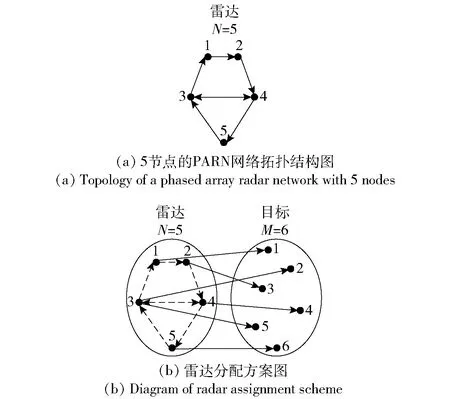
图1 雷达网络及雷达分配方案的图形化表示示例Fig.1 Graphical representation of radar network and radar assignment scheme

在雷达网资源管理问题中，可以用一个二部图[11]：Gas={Θ∪Φ,Γas}来表示雷达分配方案，Φ={1,2,…,M}是目标集，Γas⊆N×M是二部图中由雷达集到目标集的有向边集合，每一条边表示一个雷达与目标配对。此外在G和Gas中，Θi表示所有能与雷达i进行信息传输的节点集合，数量大小为|Θi|. 图1(b)所示是一个包含5个雷达节点、6个目标的雷达分配方案图。

(1)

1.2 SPARN分布式资源管理的一致性需求分析

系统的一致性是指系统中所有个体通过信息交换与融合，最终使全部个体的决策或者状态等趋于一致[12]。一致性问题是分布式系统和分布式决策的重要内容，也是分布式计算的基础，在无人飞行器控制、人造卫星簇控制等多智能体系统中得到了越来越广泛的应用研究[13-14]。在多智能体系统中，智能体之间的局部通讯协议(或者智能体网络拓扑结构)最为关键，它体现了智能体之间局部信息交换的过程，这可以用上述图论基础来表示。

SPARN是多智能体系统的一种，对其进行分布式资源管理是相对于集中式资源管理结构而言的。集中式结构有一个唯一的中央融合中心，各雷达节点把目标状态等信息传送到该中心，由中心进行信息融合并作出资源管理决策。而分布式结构没有中央融合中心，由各单雷达作出关于整个网络的资源管理决策，并且只与特定节点进行信息传输和交换。图2为两种结构的示意图。

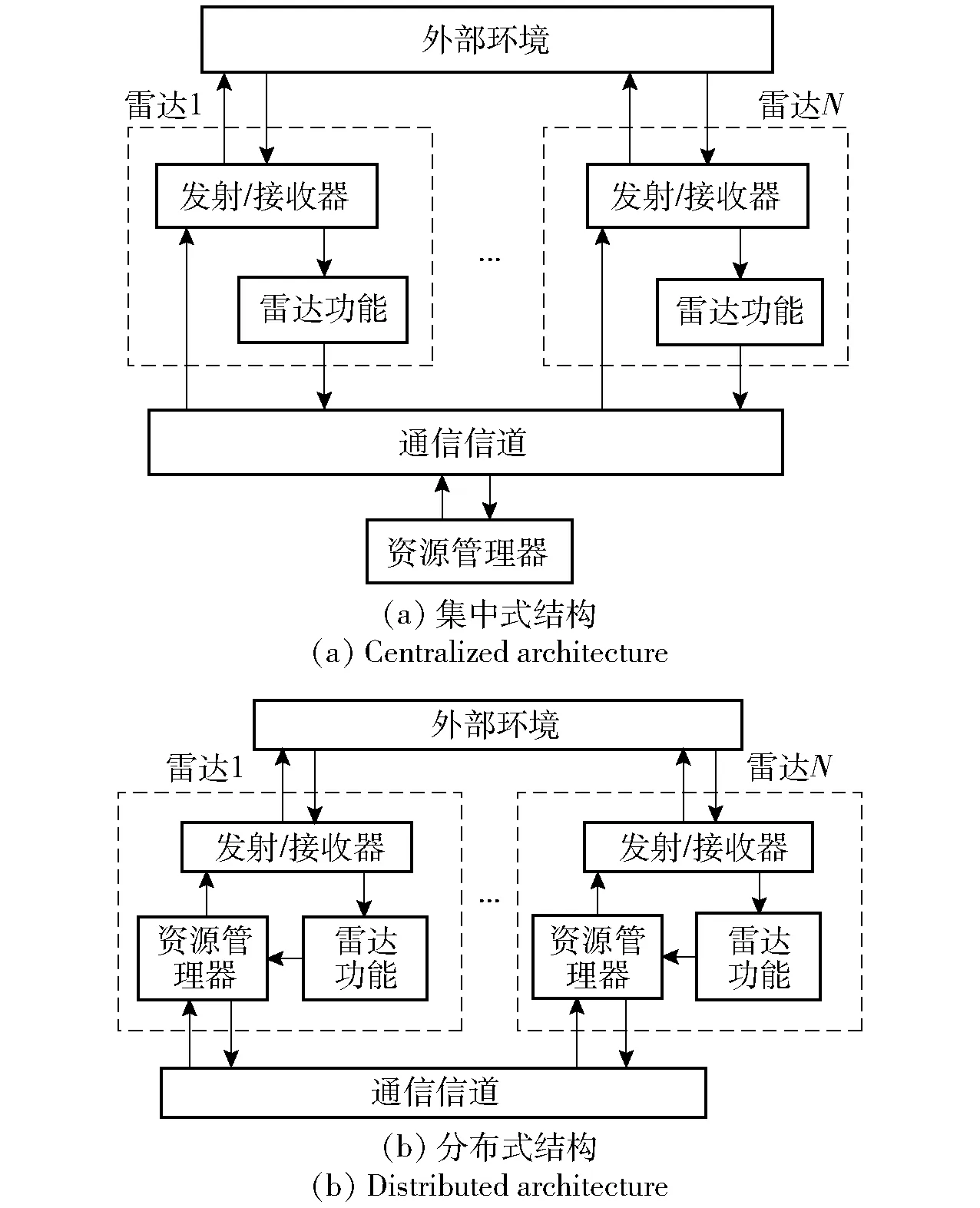
图2 雷达网资源管理结构Fig.2 Resource management architecture of radar network

在分布式资源管理过程中，根据SPARN拓扑结构的不同，各雷达节点能够获取的信息集分两种情形：1)网络是连通图结构，各节点能够获得相同的全局信息,但是会受到传输噪声的影响；2)网络不是连通图结构，各节点得到不同的信息集，同时受到噪声的影响。两种情况下，各雷达都对其他节点的资源情况以及状态信息等存在估计偏差，会导致资源管理过程中各节点给出的雷达分配方案不一致。因此，必须构建SPARN资源管理的一致性算法，运用该算法通过各雷达节点间的信息交换和传输，得到一个全局一致的分配方案。

2 本地资源管理优化

2.1 雷达资源模型

PAR资源通常包括时间资源、能量资源、计算资源3种，而时间资源是限制其执行任务能力的主要因素。本文主要从时间资源角度考察其带给PARN资源管理的限制。

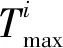
当雷达未跟踪目标时，一直在执行搜索任务，根据雷达方程，信噪比[16]可以表示为

(2)

式中：Pa是发射信号平均功率；Ar是接收天线面积；v是目标的雷达散射截面积；K是玻尔兹曼常数；Te是噪声温度；Ls是系统总损耗；Ω是最大探测距离为l时的雷达搜索空域立体角；ns是脉冲重复次数，设置为1；Ts是搜索时间。由此可得到雷达i对其搜索空域的总搜索时间表达式为

(3)

(4)

对于舰载PAR，因其采用雷达阵面共形设计，可实施360°扫描，Ω应为其全向扫描的空域立体角。此外，(4)式中的各参数是假设已知且固定的。

一旦有目标被探测并完成了跟踪起始，雷达波束会直接指向目标进行跟踪，以完成目标状态更新[16]，则有

(5)

式中：R是雷达目标距离；Gt是发射天线增益；Tt是对某一目标执行一次跟踪采样的时间，

Tt=cR4，

(6)

(7)

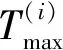
(8)

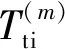
在TAS模式下，雷达占空比决定了PAR的时间资源[16]满足以下条件：

(9)

因此雷达i的时间资源使用率Pi及其限制条件可以表示为

(10)

2.2 本地资源管理模型

因为雷达资源有限而目标数目众多，且随机出现新生目标，所以需要在确保完成任务前提下，尽量占用少的雷达资源并使各雷达负载均衡。本地资源管理优化模型的目标函数就从均衡雷达负载和资源消耗最小两方面构建。

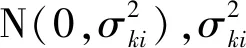
ki=Pi+wki.

(11)

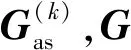
(12)

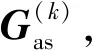
(13)

(14)

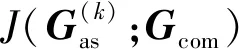
(15)

(16)

式中：Vim=1表示雷达i与配对的目标m必须具有可见性。

对于该资源管理优化模型，运用遍历算法求解会产生巨大的运算量，因此采用文献[17]中的遗传算法求解模型，以提高求解效率。

3 分配方案一致化

3.1 一致化算法

由于各节点对其他雷达的资源估计可能存在偏差，导致不同雷达给出的本地优化分配方案不一致。为有效实施资源管理，必须使各差异化的本地方案达到一致。

Ak∈N×M是只包含0、1元素的邻接矩阵。无论G属于哪种网络拓扑结构，其中各雷达向邻近节点传输分配方案信息时都会受到传输噪声干扰。假设qki(n)是雷达k在第n次迭代中向雷达i传输信息时的信道噪声。由于传输噪声通常在信号频带上具有平滑的功率谱密度，且呈现电压零均值分布，通常将其视为拥有恒定方差的零均值高斯白噪声。

根据雷达网的拓扑结构，节点i只能接收其邻近节点集合Θi中的节点所传输的信息。假设ki(n)表示雷达i在第n次迭代中接收雷达k所传输的分配方案信息，将其表示为

ki(n)=Ak(n)+qki(n),k∈Θi，

(17)

式中：Ak(n)是雷达k在第n次迭代的分配方案信息。

构建一个在每个元素上执行0-1条目的判定函数Dec(·)，其判定规则为

(18)

随着时间步长的推进，每个雷达可以通过接收到的信息来逐步更新其本地雷达分配方案，即

(19)

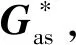
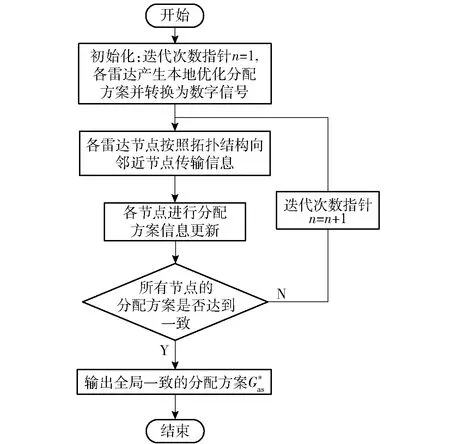
图3 一致性算法流程图Fig.3 Flow chart of consistency algorithm

3.2 算法收敛性分析

(19)式所示的各节点分配方案更新过程，可以表示为

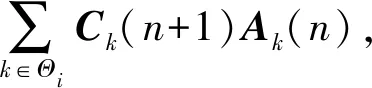
(20)

式中：Bi(n+1)为第n次迭代过程中Ai(n)的系数矩阵；Ck(n+1)为Ak(n)的系数矩阵，二者均为0-1矩阵。

δi(n+1)=Ai(n+1)-A*.

(21)

根据(20)式，(21)式可表示为

δi(n+1)=Bi(n+1)δi(n)+

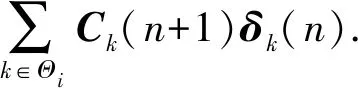
(22)

进一步，将(22)式向前推导，可得

δi(n+1)=Bi(n+1)Bi(n)×…×Bi(2)δi(1)+

(23)

‖δi(n+1)‖=‖Bi(n+1)‖‖Bi(n)‖×…×

‖Bi(2)‖‖δi(1)‖+

‖Ck(2)‖‖δk(1)‖.

(24)

由于系数矩阵都为0-1矩阵，有‖B‖≤1、‖C‖≤1. 当迭代次数n逐渐增大时，有

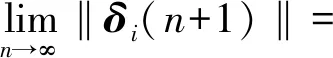
(25)

表明节点i的分配方案最终收敛于A*. 同理，网络中其他节点的分配方案通过迭代最终也收敛于A*.

此外，在利用本文算法进行状态更新的过程中，各节点的信息传输严格按照网络拓扑结构进行，且考虑了噪声影响，因此理论上该算法对不同雷达网络拓扑结构都具有适用性。

4 仿真验证与分析

4.1 有效性验证

首先对本文方法的有效性进行仿真验证。设置4个飞行目标在一个500×500的坐标网格内机动，目标状态用(x,x′,y,y′)表示，跟踪外推预测和滤波过程采用卡尔曼滤波，过程噪声方差和初始协方差分别为

每个目标初始位置随机，初始速度随机为0～5网格/s，每个目标的跟踪采样间隔为1 s.

SPARN由8个节点组成，可以监视整个网格区域并对4个目标进行持续跟踪。设置每个节点的探测空域为以该节点为圆心、半径250的圆形区域，波束照射区域表面积为50×50个坐标网格。各雷达最大搜索帧周期为10 s，最大平均功率60 kW，基准信噪比20 dB，对飞行目标的量测噪声方差为diag[100,100]. 此外，雷达网络拓扑结构为有向图，其表示信息传输关系的邻接矩阵为

仿真过程持续30 s，雷达网络布局以及0～30 s之内各目标运动轨迹如图4所示。由于舰船的机动速度相对于飞行目标而言很小甚至可以忽略，将各舰载雷达节点假设为静止状态。

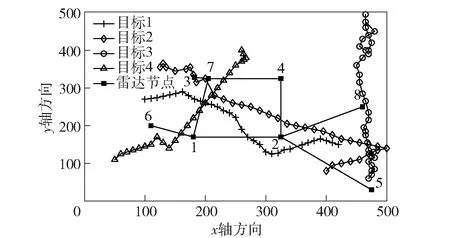
图4 目标跟踪轨迹及舰载雷达网络布局Fig.4 Target tracking trajectory and radar network topology

假设网络信息传输噪声方差统一为0.1；雷达k对雷达i资源使用率估计偏差wki的方差在(0,0.1]之间取随机值。对于本地资源管理优化模型，采用参数设置如表1所示的遗传算法进行求解。

表1 遗传算法参数设置

利用本文算法得到的仿真时间内每一时刻的雷达分配方案如图5所示。表2为15 s、30 s两个时刻，各节点的本地分配方案和全局分配方案对比。

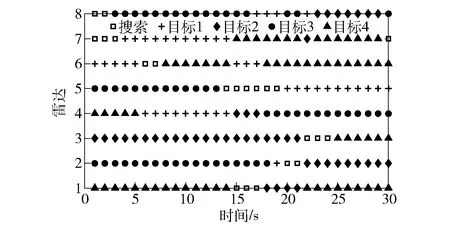
图5 全局一致的雷达分配方案Fig.5 Global-consistency radar assignment scheme

结合图5和表2可以看出：当不进行一致化时，各节点给出的本地优化分配方案具有差异性，这与协同资源管理的目的不相符；而进行一致化后，能够产生全局唯一的分配方案。此外，从图5中可以看出：所有目标在任一时刻都至少有一个雷达对其进行跟踪，以确保跟踪效果；同时由于跟踪任务更加消耗资源，当雷达网络负载不均衡或者总资源占用量过大时，会在保证目标跟踪状态的情况下使部分雷达处于搜索状态，例如雷达2在20～21 s时刻、雷达3在22～24 s时刻执行搜索任务。该仿真结果表明本文算法能够有效进行SPARN资源管理。

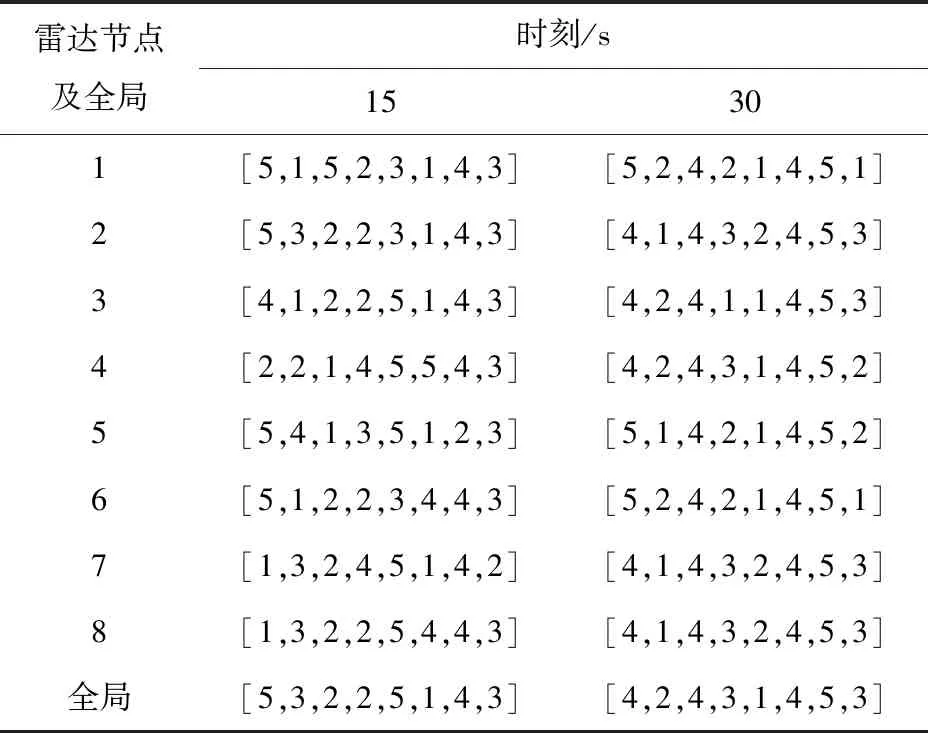
表2 本地分配方案和全局分配方案对比

注：中括号内由前至后分别为雷达1～雷达8的跟踪目标编号，编号5表示执行搜索任务。

4.2 性能对比

本文算法属于雷达网协同资源管理，仿真中将该算法与各雷达独立资源管理[4]进行比较。仿真参数设置与实验1保持不变，对两种情况分别进行100次蒙特卡洛仿真。

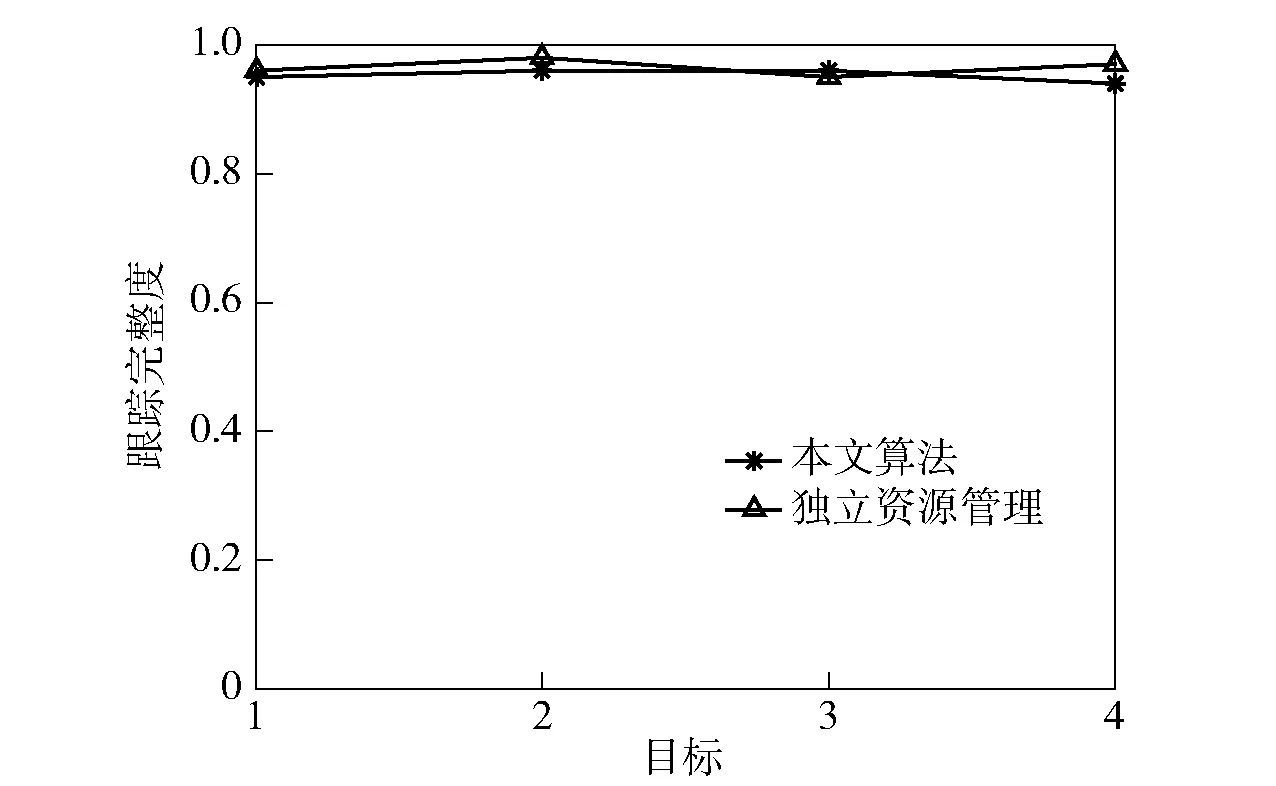
图6 目标跟踪完整度对比Fig.6 Comparison of target tracking completeness

图6、图7分别为两种算法下的目标跟踪完整度、雷达平均跟踪占有率[4]对比。结合图6、图7可以发现：利用本文算法和独立资源管理所得到的目标跟踪完整度都接近于1，二者都对目标有较好的跟踪效果；本文算法下的平均跟踪占有率在0.2～0.3之间，而进行独立资源管理时的平均跟踪占有率在0.3～0.4之间波动。该仿真结果表明，本文算法与独立资源管理相比，能够在消耗更少资源的情况下获得近似的跟踪效果，这种性能优势在目标更为密集的环境下会更加明显。

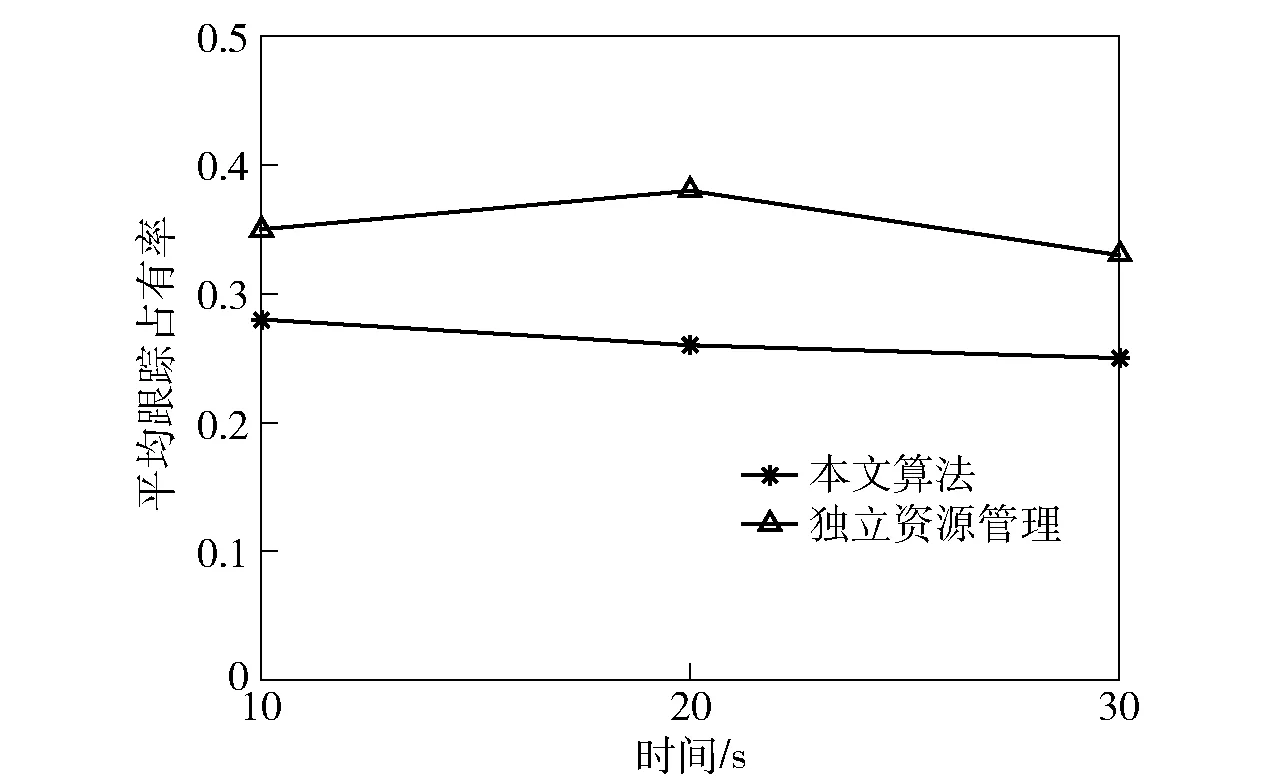
图7 雷达平均跟踪占有率对比Fig.7 Target tracking occupancy

4.3 算法适用性验证

在有效性验证中，雷达网络拓扑结构为有向图，信息传输噪声方差为0.1. 为验证本文方法对于不同SPARN拓扑结构的适用性，另设置一组仿真实验：雷达4部，随机产生15个目标，在6种不同的网络拓扑结构与信息传输噪声组合下(见表3)，分别利用本文算法进行资源管理实验，不断增加迭代次数，考察各种组合达到一致性的情况。

表3 网络拓扑结构和信息传输噪声组合

其他参数设置与实验1保持不变，进行100次蒙特卡洛仿真。不同组合下利用本文算法达到一致性情况如图8所示。

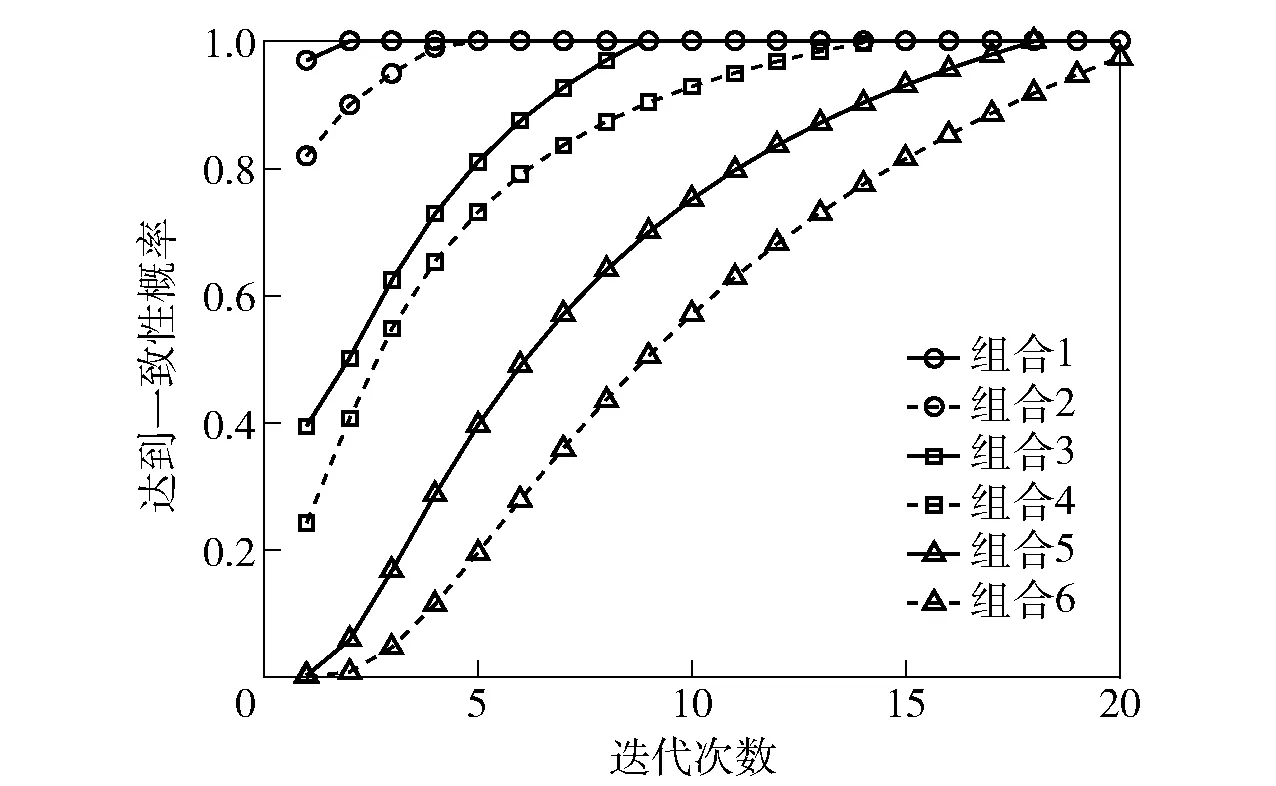
图8 一致性情况对比Fig.8 Comparison of consistency behaviors

由图8可以看出，在不同组合下利用本文算法都有至少95%的概率达到全局一致性，表明本文算法对于不同组合都具有有效性。此外，不同组合下网络达到一致所需的迭代次数对比如表4所示。

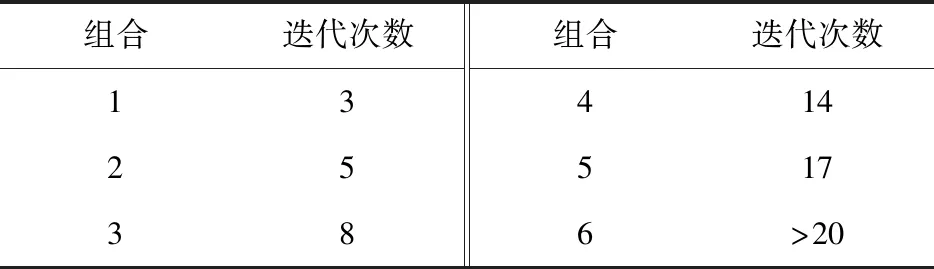
表4 网络一致化所需迭代次数

综合表4和图8可以看出：当拓扑结构为连通图、噪声方差为0.15和0.20时，网络分别经3次和5次迭代达到一致；当保持噪声方差为0.15，拓扑结构分别为连通图、有向强连通图、有向图时，网络分别经3、8、17次迭代达到一致。这表明，相对于传输噪声变化，拓扑结构变化对网络一致化性能的影响更大。这是因为拓扑结构的变化直接对节点间的信息传输方式以及连通性产生影响，当连通性变差时，对其他节点的资源使用估计会产生更大误差，需要更多迭代次数才能使网络达到一致。此外还可以看出，由连通图结构到有向强连通图结构再到有向图结构，网络的一致化性能呈递减趋势。这是因为连通图结构中每个节点都能获取全局信息，因而各本地优化分配方案间差异最小，使其一致化速率最快；相反，有向图结构中，各雷达对其他节点的资源估计变差最大，一致化速率最慢。

该仿真结果表明本文算法对于不同拓扑结构、信息传输噪声的SPARN都具有适用性；网络拓扑结构对于算法性能的影响较大，而算法在连通图形式的网络拓扑结构下性能最好。