基于多体动力学的节能型膜系统运动机构分析

王 祺，张洪伟*，窦艳涛，俞建荣，冯昆鹏，王 琳

(1.北京石油化工学院，北京 102617；2.碧水源科技股份有限公司，北京 102206)

近年来，随着污水处理市场的不断扩展，传统的污水处理工艺已经无法满足当前水质安全保障的需要，依靠膜技术作为技术内核的污水治理技术取得飞速的发展[1-2]，其中以膜作为关键核心的污水处理系统是当前环境下一种典型的和更加高效的水处理技术。

污水处理膜系统相比传统除污能够更好地实现污染物与水的分离效果，当前污水处理系统多采取曝气式的方法对污水进行处理，即鼓风机抽取外界空气并通过输气管道输送到设在池底的曝气装置中，以气泡形式弥散逸出，从而保证对象物料与膜丝的充分接触。但是，这种曝气方式通常消耗大，不符合现代节能环保理念；并且膜处理随之会带来膜污染，经过长时间处理后，膜层会形成厚的污染层，导致通量降低、效率下降。因此，众多学者针对曝气对膜污染的影响进行了大量研究。王运超等[3]研究了动态曝气对于膜污染的作用，提出了降低能耗的可能性并给出了可行建议。魏进等[4]归纳了曝气过程对膜污染的主要影响，并提出控制膜污染的因素，为后续研究提供了技术参考。

为了降低能耗，笔者设计了一种基于曲柄滑块式的膜系统往复运动机构，以机械运动的形式代替曝气，取得相同的效果[5]，运行机理为在滑行架带动下膜系统朝前后进行往复运动，并赋予惯性力，从而去除形成在所述膜表面的污染物质，这种低频运动能够有效地降低能耗，且大幅度提高治理效率，而往复机构的关键在于能否长期平稳的运行，为此，采取多体动力学与有限元分析结合的方法对膜系统机构的运动过程进行模拟与分析，运动分析结果为后续工作提供数据支撑。

1 多体动力学简介

多体动力学是一门研究多体系统运动规律的科学，多体系统即多个物体相互连接组成的系统，主要研究系统的运动学及动力学关系[6-8]。一般包括多刚体动力学系统与柔体动力学系统2大类。刚体动力学在研究过程中忽略物体的变形，将其假设为刚体。而柔体动力学则需要考虑物体的变形及应力情况。另外，在分析过程中，有些物体可作为刚体，而有些物体可作为柔性体处理，称之为刚柔耦合多体动力系统[9-12]。

多体动力学的关键在于建模方法与数值计算，其中建立正确的系统动力学方程尤为重要，对于复杂的动力学方程，需要依靠计算机的辅助[13-15]，笔者采用ANSYS Workbench进行机构的动力学分析，建模重点在于各类运动副的创建，包括转动副、移动副等。动力学分析结果包括某个构件或某个点的位移、速度、加速度以及某些运动副处的约束力、约束力矩等。

2 膜系统多体模型建立

利用曲柄滑块机构设计了一种基于连杆式的往复运动膜系统。主要包括驱动装置、传动装置、箱体滑行架及膜系统。系统运动形式基于曲柄滑块机构，即先通过法兰的回转运动，再转化为连杆的往复式直线规律运动，最后通过连杆作用于滑行架，滑行架带动整个膜系统进行往复直线运动。

利用SolidWorks建立机械运动式膜系统多体模型，将装配体模型导入Workbench中进行多体动力学仿真分析，膜部件具体结构没有考虑，仅考虑其重量作用，没有考虑电机、减速机具体结构，将其作为动力源输入条件。结果如图1所示。

图1 简化多体模型Fig.1 Simplified multi-body model

运用 ANSYS Workbench 软件中Rigid Dynamic分析模块建立6个旋转副约束、2个固定约束以及4个移动副约束，关节副如图2所示。2个固定约束：轴承座与曲轴固定连接。6个旋转副：地面与法兰设置为旋转副，连杆前段与法兰设置为旋转副，连杆后端与轴承座曲轴设置为旋转副。4个移动副：滑轮与地面设置为移动副。

图2 关节副Fig.2 Joint vice

3 膜系统动力学分析

根据往复机构的运动状态可将其简化为对心曲柄滑块机构。曲柄滑块机构由曲柄(法兰或偏心轮)、连杆、滑块通过移动副和转动副组成，如图3所示。其运动分析包括位移分析、速度分析、加速度分析。先建立机构位置与时间的方程，再对时间求导，得到速度方程，再对速度方程进行时间求导，得到加速度方程。曲柄滑块系统只有一个自由度，所以只有一个自变量，取角速度ω，根据条件建立运动参数与自变量之间的数学关系。

图3 对心曲柄滑块机构简图Fig.3 Schematic diagram of center crank slider mechanism

3.1 数学模型建立

图4 位移随时间曲线Fig.4 Displacement curve over time

图5 速度随时间曲线Fig.5 Speed curve over time

利用Matlab软件对理论模型进行解析求解，求解运行过程的滑块位移、速度及加速度，结果如图4、图5、图6所示。设置模型中曲柄长度r=0.05 m，连杆L=0.25 m，曲柄角速度ω=30 r/min。待求参数：滑块位移x、滑块速度v、滑块加速度a。建立平面直角坐标系，如图3所示，得到滑块位移x：

图6 加速度随时间曲线Fig.6 Acceleration curve over time

对曲柄滑块机构进行速度分析，式(1)对时间t求导可得到滑块速度v：

(2)

对曲柄滑块机构进行加速度分析，式(2)对时间t求导可得到滑块加速度a：

(3)

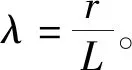
3.2 运动结果分析

针对建立的机械式膜系统模型，在法兰处施加恒定角速度30 r/min，进行多体动力学仿真，如图7所示。以往复机构的位移、速度和加速度作为求解项，计算获得机构的运动特性曲线，结果如图8～图10所示。对比可得Workbench求解数据曲线与Matlab解析解曲线基本吻合，且符合对心曲柄滑块运动学规律，证实了有限元分析的正确性，为后续复杂结构的仿真提供了参考与支撑。

图7 多体动力学模型 Fig.7 Multi-body dynamics model

图8 滑行架的位移变化曲线Fig.8 The displacement curve of the glide frame

图9 滑行架的速度变化曲线Fig.9 The velocity curve of the rack

图10 滑行架的加速度变化曲线Fig.10 The acceleration curve of the carriage

由图8可以看出，滑行架从最左端移动到最右端时，曲线斜率从零逐渐增加再逐渐减小，移动到最右端时曲线斜率为零。此时滑行架速度为零。在该范围内，速度方向为负X轴，速度逐渐增大再逐渐减小为零。滑行架从最右端移动到最左端时，曲线斜率从零逐渐增加再逐渐减小，移动到最左端时曲线斜率为零。此时滑行架速度为零。在该范围内，速度方向为正X轴，速度逐渐增大再逐渐减小为零。滑行架回到初始位置并开始下一个周期循环。

由图9可以看出，在0～0.5 s和1～1.5 s之间，滑行架速度各出现一个负极值-3.323 m/s和正极值3.329 m/s。且观察发现，滑行架从最右端极限位置运动到最左端位置的平均速度略大于从最左端极限位置运动到最右端位置的平均速度，也就是说滑行架空回行程的平均速度大于工作平均速度。因此对于往复机械式膜组设备，尽可能选择对心曲柄滑块机构，保证构件传力性能较好；对心曲柄机构中加速度近似左右对称；偏置曲柄随偏心距离增加，左右不对称现象增加，速度波动增加。

通过加速度曲线(图10所示)可以研究膜系统工作时往复运动产生的惯性力。在往复运动中惯性力的影响对能否平稳运行十分重要，惯性力是指当物体有加速度时，物体本身具有的惯性会使物体倾向于维持当前的运动状态，即惯性力的方向与加速度方向相反，所以通过加速度的方向走势可以判断惯性力的方向。在左极限点前后滑行架加速度方向是右行的方向，往复惯性力向左；在右侧极限点前后加速度方向是左行的方向，往复惯性力向右。左右极限位置往复瞬间惯性力最大。

往复加速度理论上与角速度的平方正相关，所以曲柄的角速度的变化，对于加速度影响尤为明显，角速度峰值出现时间与加速度峰值时间基本一致。

4 结论

(1)设计了一种往复运动膜系统，利用惯性力作用减少膜污染。运用Matlab对理论模型进行求解，得出相关运动参数，再用ANSYS Workbench对结构进行动力学仿真，通过对比计算参数是否一致来验证ANSYS Workbench动力学仿真的正确性。

(2)将多体动力学及有限元法引入到污水处理用膜系统机械运动机构的运动分析中。运用 ANSYS Workbench 中 Rigid Dynamic 模块对往复式结构进行动力学分析，包括位移曲线、速度曲线、加速度曲线及惯性力随时间变化的过程，了解往复式机械结构的整个运动过程，对结构设计提供指导。

(3)以往的刚柔耦合分析都是基于Adams与ansys的联合仿真，数据与结果来自不同的软件处理，会带来一定数据偏差，现在用Workbench自带模块Rigid Dynamic 仿真，使仿真结果更加准确，为污水处理用膜系统机械往复运动机构的后续开发与优化提供可靠的数据支撑。