基于关联规则的土石坝渗流推理预测方法及应用

李 俊,苏怀智,2, 周仁练

(1.河海大学水利水电学院,江苏 南京 210098; 2.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)

我国已建大坝9.8万余座,其中绝大多数为土石坝。渗流是影响土石坝安全的重要因素之一,土石坝的各种破坏形式都直接或间接与渗流有关,所以准确预测渗流量的大小对实现土石坝的安全监控有着重要意义[1-2]。根据已建立的渗流量统计模型,土石坝渗流量主要受上下游水位、降雨入渗以及坝前淤积和防渗体的时变过程等影响[3-4]。但土石坝渗流性态受多种因素的影响,预测难度很大[5]。

目前,界内对于渗流预测的研究主要集中在神经网络、时间序列、回归分析等方面,这些方法或多或少存在一定的缺陷。神经网络存在收敛速度慢、泛化能力弱等缺点;时间序列预测方法在处理模糊数据时可能会出现模型过度拟合的危险;回归分析需要建立复杂的数学模型,通过求解线性方程组得到各个回归系数,当线性方程组出现病态或奇异时,回归方法是无法处理的[6-12]。1993年,Agrawal等首先提出关联规则的概念。关联规则是形如X→Y的蕴涵式,即由事物X推导出事物Y。其中,X和Y分别称为关联规则的先导和后继,并且关联规则X→Y存在支持度和信任度。Apriori是一种经典的关联规则算法,用于挖掘大数据中潜在的事物联系。该算法采用自底向上的遍历思想逐级挖掘,以确保关联规则的准确性。针对经典Apriori算法执行效率低的缺点,周发超等[13]引进TID标识码,使得算法效率大大提高;林郎碟等[14]将Apriori算法应用于图书推荐服务中,结合“分割-整合”的思想,为建设智能图书推荐系统打下理论基础;Guo等[15]将温度、湿度、气压和风速打包成事务组,进行短期风速预测,将预测结果用于校正由混沌时间序列所预测的结果,取得较好的预测精度。本文将Apriori算法用于挖掘环境量(包含上下游水位、降雨量等)与渗流量之间的内在关系,建立推导法则,从而为大坝渗流监控和预报提供一种新途径。

本文的主要思路是利用某土石坝实测数据建立预测模型,然后检验该模型的预测精度并给予评价。在对实测数据进行预处理时,首先分析环境量和渗流量的相关关系,用K-means聚类算法对环境量和渗流量进行离散化处理,然后将处理过的数据转换成Apriori算法能够识别的布尔型矩阵进行关联规则的挖掘,最后将关联规则用于渗流量的预测。通过实例演示和精度分析,证实了该预测模型具有较好的预测精度。

1 土石坝渗流监测数据预处理

1.1 渗流量与环境量相关关系及滞后性分析

本文仅考虑渗流量受上游水位、降雨量和下游水位的影响[3]。当环境量(上游水位、降雨量和下游水位)发生变化时,渗流量不会立刻响应,所以在进行关联规则挖掘时,在同一组数据内,环境量和渗流量不应是同一时间,环境量应较渗流量有所提前,此性质恰好可以用于建立预测模型[16]。需要注意的是,环境量相对渗流量提前的时间也各不相同,应根据环境量的性质分别计算。

1.1.1上游水位

上游水位是影响渗流量大小的重要因素,显然,在其他环境量保持稳定的前提下,渗流量与上游水位呈正相关关系。有两种方法估计上游水位的渗流响应滞后时间:

a. 利用大坝泄流。水库一般会在雨季来临之前或者需要放水抗旱时大量泄流以降低库水位,根据工程经验,一段时间后,坝体渗流量也会随之下降。所以,选取某一次泄洪前后且无降雨的时间段内一组数据,直接观察渗流量变化滞后的时间,即为上游水位的渗流响应滞后时间。

b. 利用稳定数据。如果没有合适的泄洪时间段,那就只能选用多段稳定数据来估算。当水库不泄洪且无降雨时,水库水量损失主要是因为蒸发和渗流,水库水位会稳步下降,渗流量也会相应变化。可以选取多段无降雨时段,观察渗流量的滞后时间,取均值(以天为单位,取整)作为上游水位的渗流响应滞后时间。

1.1.2降雨量

降雨量对土石坝渗流量的影响较为明显,也比较容易判断渗流响应滞后时间。选取前后一段时间均无降雨,且上下游水位变化幅度较小或变化稳定的短时降雨,观察渗流量响应时间,作为降雨量的渗流响应滞后时间。

1.1.3下游水位

通常情况下,下游水位变化不大,所以该模型不考虑下游水位的渗流响应滞后时间。为了方便建模,下游水位取与上游水位对应的同一天的值。

1.2 实测数据离散化

关联规则算法不具备处理连续数据的能力,所以在进行关联规则的挖掘前,应先将实测数据进行离散化处理。所谓离散化,即将连续型环境量(或渗流量)所处的区间,利用K-means算法划分成多个短区间(簇),所处同一短区间(簇)的数据归为一类,用区间编号代替。K-means是一种基于形心的划分算法,使用簇Ci的形心代表该簇。K-means算法把簇的形心定义为簇内点的均值[14]。

以渗流量为例介绍该算法的处理流程。假设m天的渗流量实测数据需要划分为k个簇,随机选取k个数据,每个数据作为一个簇的初始形心,对剩下的每个数据,根据其与各个簇中心的距离,把他分配到最相似的簇。然后,对于每个簇,使用上次迭代分配到该簇的对象,计算新的均值。然后,使用更新后的均值作为新的簇中心,重新分配所有对象。继续迭代,直到分配稳定,即本轮形成的簇与前一轮形成的簇相同[17]。

1.3 布尔型转换

将实测数据聚类以后,为满足Apriori算法对输入数据的要求,还需要将聚类后的实测数据转换成布尔型数据,即只用0和1表示。

以渗流量和上游水位为例,简要说明转换过程。假设有m组数据,矩阵表中每一行表示同一天的监测值,每行数据均包含渗流量、上游水位、降雨量和下游水位4个变量,构成m×4矩阵A∈Rm×4。利用K-means算法将渗流量和上游水位分别划分为k1、k2类,对于矩阵中的所有实测数据,均用该实测数据所处的簇编号代替。

比如渗流量被聚类成k1类,转换成布尔型矩阵时,渗流量对应布尔型矩阵的前k1列,且每个实测数据的簇编号对应的布尔型矩阵中渗流量列编号,用1标注该列,其余列均为0。上游水位、降水量、下游水位都可用相同方法转换。

2 基于Apriori算法的土石坝渗流关联规则

利用Apriori算法挖掘关联规则可分为两步,首先挖掘实测数据中的频繁项集,然后将频繁项集推理成关联规则。支持度是指项集在数据库中出现的次数或频率,置信度是指关联规则在数据库中的准确性。算法中,所有支持度大于最小支持度的项集称为频繁项集,所有置信度大于最小置信度的关联规则称为强关联规则[18]。最小支持度和最小置信度的取值应保证算法所挖掘出来的强关联规则的数目合理,且将强关联规则用于工程预测时,预测精度要满足工程要求[19]。

利用Apriori算法产生频繁项集的过程主要分为连接和剪枝两步:首先,将包含i个变量的项集称为i-项集,将包含i个变量的频繁项集称为i-频繁项集,扫描所有实测资料,产生候选1-项集,根据最小支持度,产生1-频繁项集。然后由1-频繁项集自连接产生2-项集,对2-项集剪枝处理,即剔除2-项集中有非空子集是非频繁项集的项,再根据最小支持度,产生2-频繁项集。重复以上步骤,直到得出包含上游水位、降雨量、下游水位和渗流量4个变量的4-频繁项集[20]。

图1 预测流程

然后由频繁项集产生强关联规则,例如2-频繁项集(U,S),其中U为取值在区间[a,b]内的上游水位;S为取值在区间[c,d]内的渗流量。

则关联规则由U推导出S的支持度SS和置信度CC的计算公式分别为:

SS(U→S)=P(U∪S)

(1)

CC(U→S)=P(US)

(2)

该关联规则可以表述为:当上游水位在区间[a,b]内时,渗流量有P(US)的可能性出现在区间[c,d]内,且这种情况出现的频率为P(U∪S)。

3 基于关联规则推理的土石坝渗流预测实现过程

综合应用K-means算法和Apriori算法,基于土石坝渗流关联规则的推理,实现土石坝渗流预测的具体流程如图1所示,主要步骤如下。

步骤1:渗流量与环境量相关关系及滞后性分析。利用前文提到的方法分别计算环境量的渗流响应滞后时间,根据滞后时间,将理论上具有因果关系的渗流量与环境量调整为同一组数据,构成新的数据组。

步骤2:聚类离散化。利用K-means算法对新的数据组进行聚类分析,并用聚类出来的簇编号代替实测数据,构成离散型实测数据矩阵。

步骤3:布尔型转换。将离散型实测数据矩阵转换成Apriori算法能识别的布尔型矩阵。

步骤4:关联规则的挖掘。将得到的布尔型矩阵作为Apriori算法的输入矩阵D,同时输入最小支持度和最小置信度进行关联规则的挖掘。

步骤5:关联规则的筛选。经过上述关联规则挖掘后,会产生多个4-频繁项集,并由此产生多种强关联规则。但是并不是所有的强关联规则都能用于预测,只有形如U、R、D→S(其中U、R、D分别为上游水位、降雨量和下游水位,S为渗流量)的强关联规则才是有用的[19]。所以需要对所产生的强关联规则进行筛选。

步骤6:渗流量的预测。对于所筛选出的强关联规则U、R、D→S,环境量均提前渗流量一段时间,设环境量提前时间分别为mU、mR、mD,若要预测某一天的渗流量,环境量应分别取mU、mR、mD前的值。显然,所产生的渗流量预测结果是一个聚类区间,而不是一个准确的值。考虑到聚类所产生的区间大小不一,不适合作为预测结果,本文采用区间上下边界的均值作为预测结果。

步骤7:预测结果评价。本文选取平均绝对误差、平均相对误差以及均方根误差作为评价指标[21]。

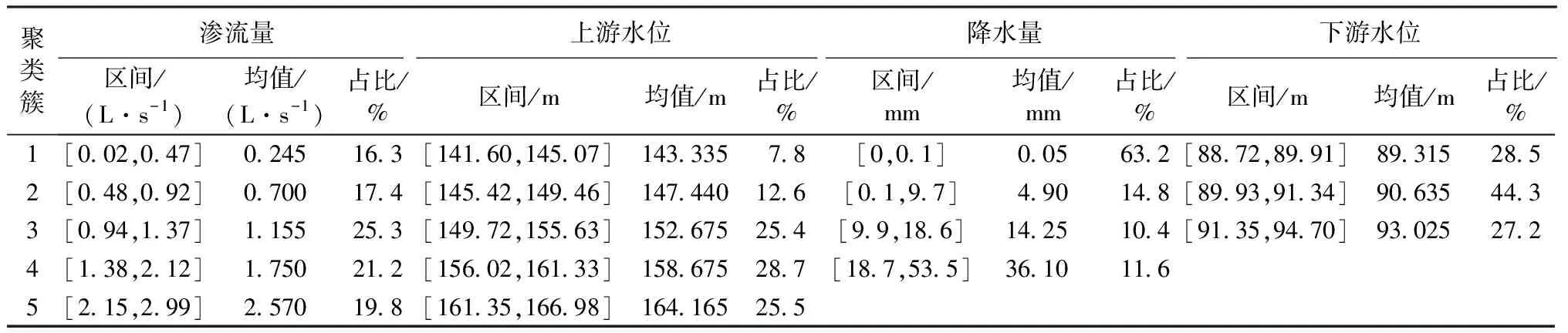
表1 K-means聚类算法对各变量聚类结果

4 工程实例分析

以某水库左岸土石坝段渗流量为预测对象。该坝段坝顶高程177.60 m,设计蓄水位170.0 m,共布设3个渗流监测点,分别监测先锋沟、左下挡和结合面部位。对先锋沟观测点在2014年7月10日至2017年12月29日期间的渗流量(L/s)进行220次观测,其中前200组数据作为训练集,后20组数据作为检验集。具体渗流量及相关环境量过程线见图2。

图2 某水库左岸土石坝段渗流量及相关环境量过程线

4.1 渗流量与环境量相关关系及滞后性分析

选取两组典型的上游水位与渗流量变化趋势,绘制成折线图,观察两组曲线的关键折点,可确定上游水位渗流量响应滞后时间为1 d,同时下游水位渗流量响应滞后时间也为1 d。

图3 典型上游水位与渗流量变化趋势

选取前后一段时间内均无降水的一次短时降水后的渗流量变化趋势图,如图4所示,观察得到降水量渗流响应滞后时间为0。在预测时,降水量的取值应根据天气预报来确定。

图4 典型降水量与渗流量变化趋势

经过上述计算,应先将当天的渗流量、降水量与前一天的上、下游水位调整为同一组数据,然后进行后续处理。

4.2 聚类离散化及布尔型转换

对渗流量及环境量用K-means聚类算法离散化,根据区间长度分别取k1=5,k2=5,k3=4,k4=3,结果如表1所示。

根据上述结果,可将200×4原始数据矩阵转换成200×17布尔型矩阵,用于关联规则挖掘。

4.3 关联规则的挖掘与筛选

将处理好的200×17布尔型矩阵作为Apriori算法的输入数据,由于最小支持度和最小置信度的取值尚无经验可循,为得到合理数量的强关联规则并达到预期的精度,经反复尝试,最终确定取最小支持度为3,最小置信度为0.6,进行关联规则的挖掘,得到18个4-频繁项集,由该频繁项集,可推导出64组强关联规则。筛选出可以用于预测的关联规则,整理结果如表2所示。表中下标表示该物理量所在的聚类簇,如表中第一行U3、R1、D1→S1表示当上游水位在区间3,降水量在区间1,下游水位在区间1时,降水量有75%的可能出现在区间1,且这种情况出现了27次。

表2 筛选出的可以用于预测的强关联规则

4.4 利用强关联规则预测及评价

由于用于挖掘的数据较少,并不能挖掘出所有环境量区间的任意组合(共有120种组合)的关联规则。所以,并不是检验集中的所有数据都能用于预测检验。只有环境量符合挖掘出的关联规则的组合,才可以预测。这里只对符合所产生关联规则的6组数据做预测,结果如表3所示。

表3 渗流量预测结果误差

由表3可知,6组数据的平均绝对误差为0.278 L/s,相对误差为17.45%,均方差为0.293 L/s,根据强关联规则所预测的结果均有较好的精度,相对误差控制在20%左右,预测精度良好。这表明,在进行关联规则的挖掘时,取置信度为0.6是足够的,若为了提高预测的准确率而过度的提高置信度,会使得可用的强关联规则数量减少,这显然是不合理的。

5 结 语

基于Apriori算法对关联规则的挖掘,本文建立了一种新的渗流量预测模型,该模型的特征总结如下:

a. 内部逻辑关系明确,易于通过各种编程软件实现。这为继续深入研究改进提供了很大的便利。

b. 预测精度高。渗流量的预测不同于坝体变形等方面的预测,渗流量的影响因素多,各影响因素之间关系复杂且变化多样,常规算法很难对渗流量进行准确预测。本文所构建的预测模型,将预测精度控制在20%左右,基本实现预期目标。

c. 通过对比相似的关联规则,可初步判断环境量与渗流量间的变化规律。例如,在表4中,对比规则5、6,可知上游水位对渗流量的影响非常显著;同样的,对比规则1、3,可知当降水量较小时,对渗流量的影响也较小。

d. 显然,增大置信度或支持度会提高模型的预测精度,但也会导致产生的强关联规则较少,即模型的可预测范围会缩小;反之,减小置信度或支持度会大幅增加强关联规则的数量,使模型预测范围扩大,但同时预测精度也会降低。所以,本模型的后续研究应该着重于置信度及支持度的大小(预测精度)和关联规则数目(预测范围)的权衡问题。