水文随机变量二维分布及其应用

芮孝芳

(河海大学水文水资源学院，江苏 南京 210098)

作为随机变量的水文要素或水文特征值之间，由于物理原因，其中有一些或多或少存在着一定的因果联系，揭示并应用这些联系来处理或解决一些水文学问题，是水文学的重要研究内容之一。笔者第一次在概率统计指导下接触这一学术领域始于我国著名水文学家刘光文先生的学术讲座。笔者已经保存了56年的听课笔记清楚地记录着，那是1963年5月20日下午，刘光文先生作了题为“二元机率分配及相关的基本概念”的学术讲座。从“二元机率分配的基本概念”，到“变数之间的关系”，刘光文先生作了缜密而富有启发的讲解，令人耳目一新，令笔者至今记忆犹新。在日后漫长的岁月中，这一讲座所涉及的内容及透视出的科学思想无时无刻不在笔者的学术生涯中起着指导性作用。刘光文先生这一学术讲座开启了我国水文学术界研究水文随机变量二维分布及其应用的先河。本文试图根据半个多世纪以来这一领域的发展和笔者的思考与实践，从概念、理论到实际应用，进一步探索二维分布在处理或解决水文学问题中的思路和方法，以期引起研究二维分布及其应用的兴趣，踏踏实实，满怀信心，走守正创新之路。

1 两个随机变量之间关系的数学描述

水文随机变量之间可能存在函数关系或相关关系，也可能相互独立。两个随机变量中，若一个随机变量X的每个现实x，都只与另一个随机变量Y的一个现实y对应，则称这两个随机变量之间为函数关系，又称确定性关系。根据物理意义，两水文随机变量的函数关系属于因果函数关系。水文随机变量随时间、空间的变化虽然也是一种函数关系，但不是因果函数关系，而是数量函数关系。两个随机变量中，若对应一个随机变量X的每个现实x，另一个随机变量Y将以不同的概率取不同的值，或者说，对应于随机变量X的每一个实现x，随机变量Y将有不同的条件分布，则称这两个随机变量之间为相关关系。两个随机变量中，若对应一个随机变量X的每个现实x，另一个随机变量Y将有完全相同的条件分布，则称这两个随机变量之间为独立关系。

两个随机变量的二维分布函数就是它们之间关系的最完整描述。因为，若两个随机变量X与Y为函数关系，则由随机变量函数的分布函数理论知，只要已知其中一个的分布函数，另一个的分布函数就可以推导出来。这表明这时二维分布实际上已退化为一维分布了。若两个随机变量X和Y相互独立，则由概率论知，二维分布将等于这两个随机变量的分布函数之乘积：

f(x,y)=fx(x)·fy(y)

(1)

F(x,y)=Fx(x)·Fy(y)

(2)

若两个随机变量X与Y为相关关系，则由概率论知，二维分布将为边际分布与条件分布之乘积：

f(x,y)=fx(x)·fy(yx)=fy(y)·fx(xy)

(3)

或

F(x,y)=Fx(x)·Fy(yx)=Fy(y)·Fx(xy)

(4)

式中：f(x,y)和F(x,y)分别两个随机变量X和Y的二维密度函数和二维分布函数；fx(x)和Fx(x)分别为随机变量X的密度函数和分布函数，或称二维分布关于X的边际密度函数和边际分布函数；fy(y)和Fy(y)分别为随机变量Y的密度函数和分布函数，或称二维分布关于Y的边际密度函数和边际分布函数；fy(yx)和Fy(yx)分别为X发生条件下Y的条件密度函数和条件分布函数；fy(yx)和Fy(yx)分别为Y发生条件下的X的条件密度函数和条件分布函数。

命题“两个随机变量之二维分布是它们之间关系的最完整描述”的科学性之所以毋庸置疑是因为，如果两个随变量为函数关系，那么其二维分布必退化为一维分布，反之，如果一个二维分布可表达为一维分布，那么这两个随机变量必为函数关系；如果两个随机变量相互独立，那么必满足式(1)或式(2)，反之，如果二维分布可表达成式(1)或式(2)，那么这两个随机变量必相互独立；如果两个随机变量之间只具有一定的相关关系，那么必满足式(3)或式(4)，反之，如果二维分布可表达成式(2)或式(3)，那么这两个随机变量之间必定只具有一定的相关关系。

因此，所谓两个随机变量之间的数学描述，实际上就是构建两个随机变量的二维分布函数。

2 二维正态分布的两个随机变量之间的关系

二维正态分布是迄今为止，为数不多的能给出解析数学表达式的二维分布，其密度函数为[1-3]：

(5)

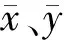
由式(5)可得，二维正态分布的两个边际分布均为一维正态分布，分别为

(6)

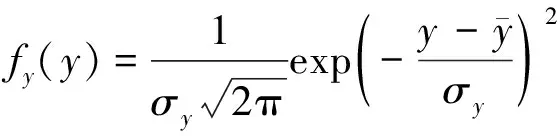
(7)

两个条件分布也都是一维正态分布，分别为

(8)

(9)

由以上两点并非充分条件，因为反之并不一定成立。

由式(5)还可以发现，当r=0时，式(5)和式(8)、式(9)将分别变为

(10)

(11)

(12)

这就说明，对于二维正态分布，两个随机变量X与Y的Pearson相关系数r=0是与式(10)～(12)完全等价的，也就是说，r=0是服从二维正态分布的两个随机变量相互独立的必要和充分条件。这个“完全等价”对不服从二维正态分布的两个随机变量则是不成立的。

进一步考察二维正态分布的条件分布，还会有新的发现。事实上，由式(8)可知，Y倚X的条件均值和条件均方差分别为

(13)

(14)

由式(9)可知X倚Y的条件均值和条件方差分别为

(15)

(16)

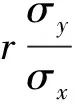
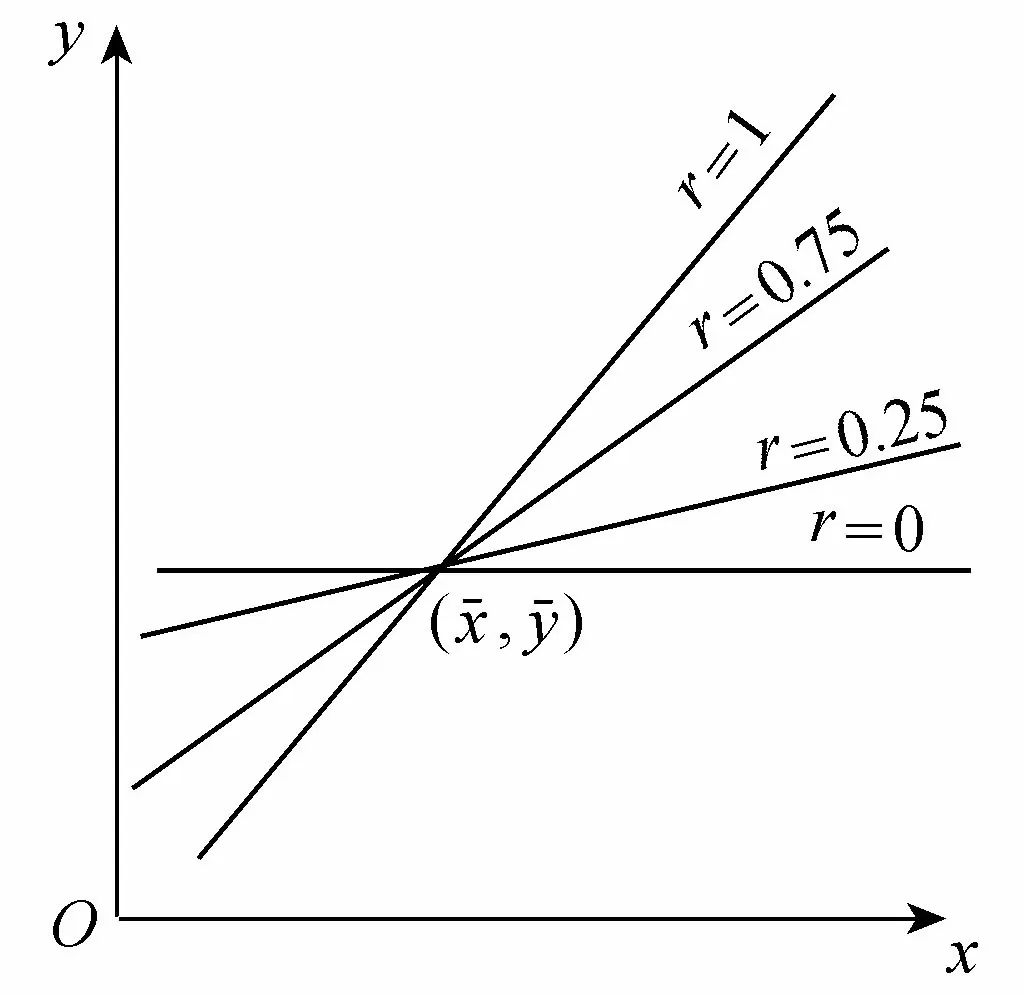
图1 二维正态分布不同r的Y倚X的回归线

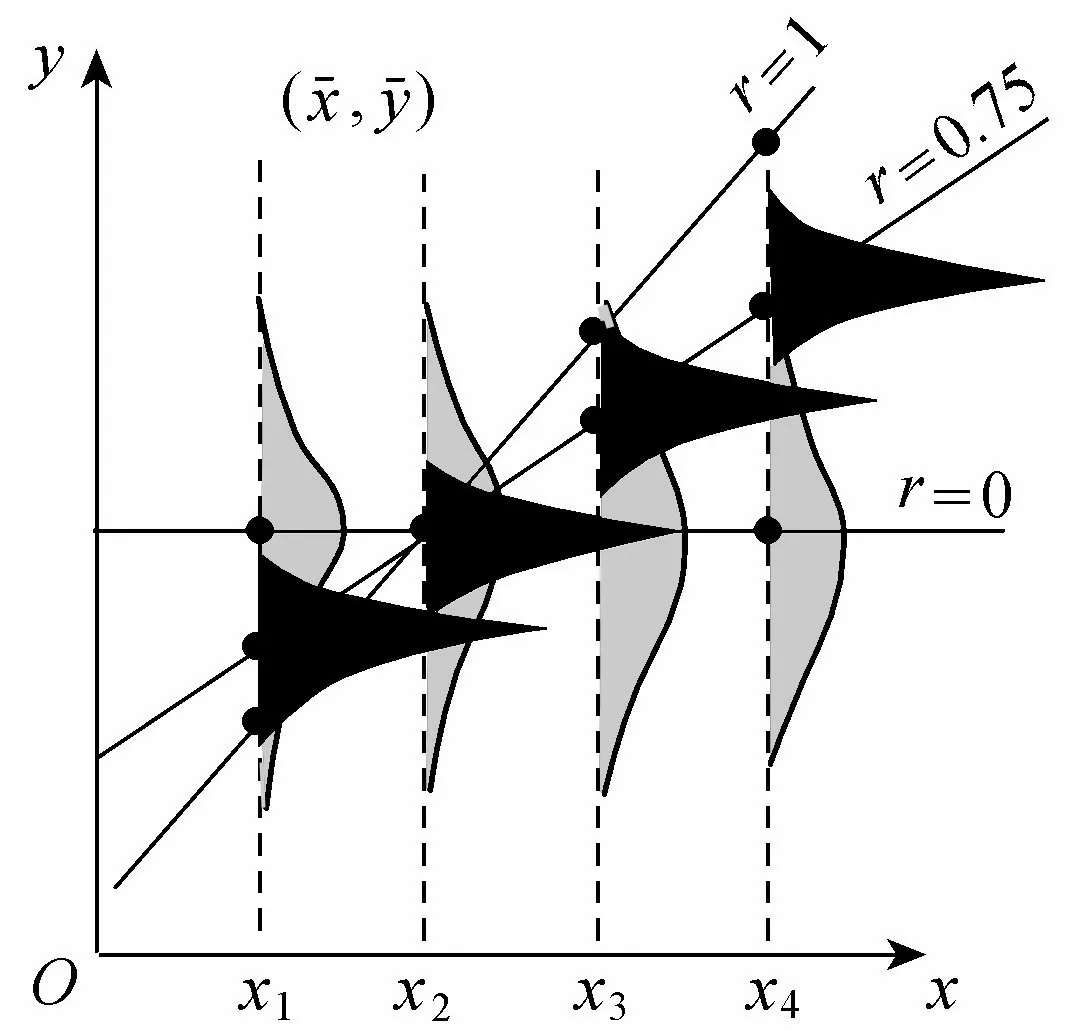
图2 二维正态分布不同r的条件密度函数

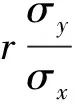
(17)

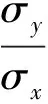
(18)

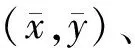
3 Copula函数理论和方法

若两个随机变量均服从正态分布，则其二维分布即为式(5)。若两个随机变量中只有一个为正态分布或者两个均不为正态分布，则其二维分布就不能用式(5)表达，在这种情况下，将如何寻找其二维分布呢？显然，寻求两个随机变量的二维分布函数一般要比寻求一维随机变量分布函数困难得多，正因为如此，在水文学中二维分布的研究相对薄弱。本节和下一节仅对确定任意两个随机变量二维分布的Copula函数和形变函数的理论和方法进行讨论。

Copula函数的起源可追溯到1959年[4],是年，Sklan指出：可以将任意一个n维分布函数分解为n个边际分布和一个Copula函数，其中边际分布描述每个随机变量的一维分布函数，Copula函数则描述这些随机变量之间的相关性。因此，Copula函数是一个将多个随机变量的一维分布“连接”成为多维分布的函数，顾名思义，可将Copula函数译作“连接函数”。Sklan这一基本思想是以定理的形式公布于世的，以构建二维分布为例就是：令H为具有边际分布F和G的两个随机变量的二维分布，那么将存一个Copula函数C，使得

H(x,y)=C[F(x),G(y)]

(19)

在式(19)中，若F和G是连续的，则Copula函数C将是唯一的。根据这一定理，可以得到如下推论：若H为具有边际分布为F和G的两个随机变量的二维分布函数，C为其Copula函数，F-1和G-分别为F和G的反函数，则对于C的定义域I2即[0,1]2内的任意(u,v),有

C(u,v)=H[F-1(u),G-1(v)]

(20)

上述Sklan定理及其推论显然表明，在两个随机变量的二维分布未知时，将可以通过边际分布和Copula函数来构建，而在二维分布已知时又可以利用边际分布的反函数求出相应的Copula函数。笔者认为，Copula函数理论提出的意义不仅在于可以通过寻找Copula函数，继而构建出二维分布，而且在于能够揭示出隐含在二维分布中过去未曾被发现的Copula函数及其所描述的相关性质。

现有的文献表明，根据生成元的不同，Copula函数可分为椭圆型、Archimede型、二次型、极值型等类型[5]。其中Archimede型Copula函数，由于构造方便，使用容易，已得到较为广泛的应用，它又有3种具体型式：

a. Gumbel-Hougaard Copula函数，公式为

(21)

式中：u=F(x);v=G(y);θ为Copuar参数，θ≥1。当θ=1时，u与v相互独立，当θ→∞时，u与v为函数关系。由于两个随机变量均为较大值时变化敏感，故式(21)能较好地描述具有上尾相关特性的两个随机变量之间的相关性。

b. Clayton Copular函数，公式为

C(u,v)=u+v+[(1-u)-θ+(1-v)-θ]-1

(22)

式中：符号意义同前述。当θ→0时，u与v相应独立；当θ→∞时，u与v为函数关系。由于两个随机变量均为较小值时变化敏感，故式(22)能较好地描述具有下尾相关特性的两个随机变量之间的相关性。

c. Frank Copula函数,公式为

(23)

式中：符号意义同前述。当θ>0时，u与v为正相关；当θ<0时，u与v为负相关；当θ→0时，u与v相互独立。由于两个随机变量无论较大值还是较小值变化均不敏感，故式(23)难以快速捕捉到两者相关性的尾部变化。

以上3种常用的Copula函数中均包含有参数θ，在数学上现已研究出了一些确定θ值的途径和方法，其中以根据Kendall秩次相关系数τ与θ之间的关系确定θ值最为常见。对于Archimede型Copula函数，其参数θ与Kendall秩相关系数τ之间的关系列于表1。

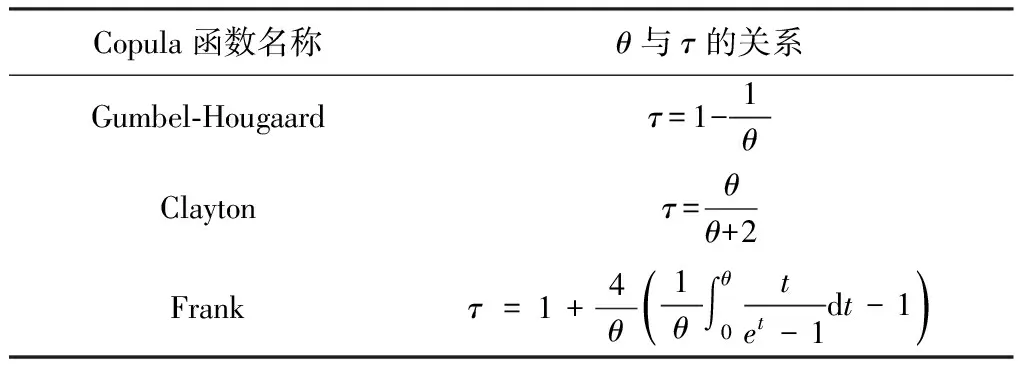
表1 Archimede型Copula函数的参数θ与Kendall秩相关系数τ的关系

Copula函数理论和方法在快速发展的金融业刺激下，已有了长足的进展，水文学中使用它仅仅是近十多年来的事。

4 形变函数理论和方法

早在1923年，Narumi就指出,在估计二维样本的联合分布即二维分布时应当考虑二维分布函数的两个最重要的数字特征：两个随机变量的回归线和条件方差[6]。前者描写了倚变量条件均值随另一随机变化的每个现实的变化；后者可看出倚变量的条件方差随另一随机变量的每个现实的变化。嗣后，1934年别伦斯谦、1954年萨尔马诺夫、1951年可历克赛也夫[7]分别根据二维分布这两个重要数字特征先后提出了刚性相关、弹性相关和挠曲相关等概念，从而丰富了Narumi的学术思想。

刚性相关是指倚变量的条件均值随另一个随机变量的每个现实而变，而条件均方差则保持不变的相关。这里回归线可为线性，也可为非线性。刚性相关的两个随机变量相关散点图如图3所示。弹性相关是指倚变量的条件均值不随另一个随机变量的每个现实而变，为常数，但倚变量的条件方差却随另一个随机变量的每个现实而变，并在引进一个变形函数后则不随另一个随机变量的每个现实而变的相关。弹性相关的两个随机变量散点图如图4所示。挠曲相关是指虽然倚变量的条件均值和条件均方差随另一个随机变量的每个现实而变，但在引进一个变形函数后可以使条件均值和条件均方差都不再随另一个随机变量的每个现实而变的相关。挠曲相关的两个随机变量相关散点图如图5所示。不难看出，刚性相关和弹性相关都是挠曲相关的特例。这3种相关虽不能盖全，但由于抓住了二维分布中条件均值和条件均方差两个最主要的数字特征的变化特点，已能适用于许多情况了，因此，若能解决这3种相关的二维分布构建问题，则就能基本上满足水文学中构建二维分布的需要了。

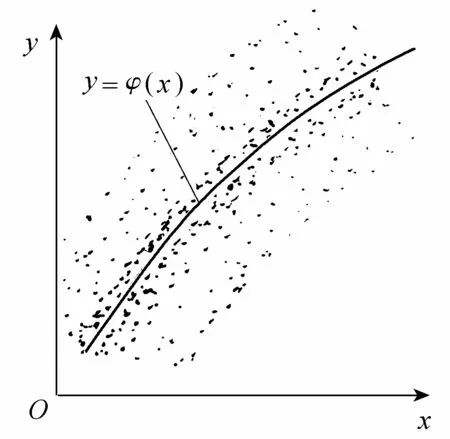
图3 刚性相关散点分布

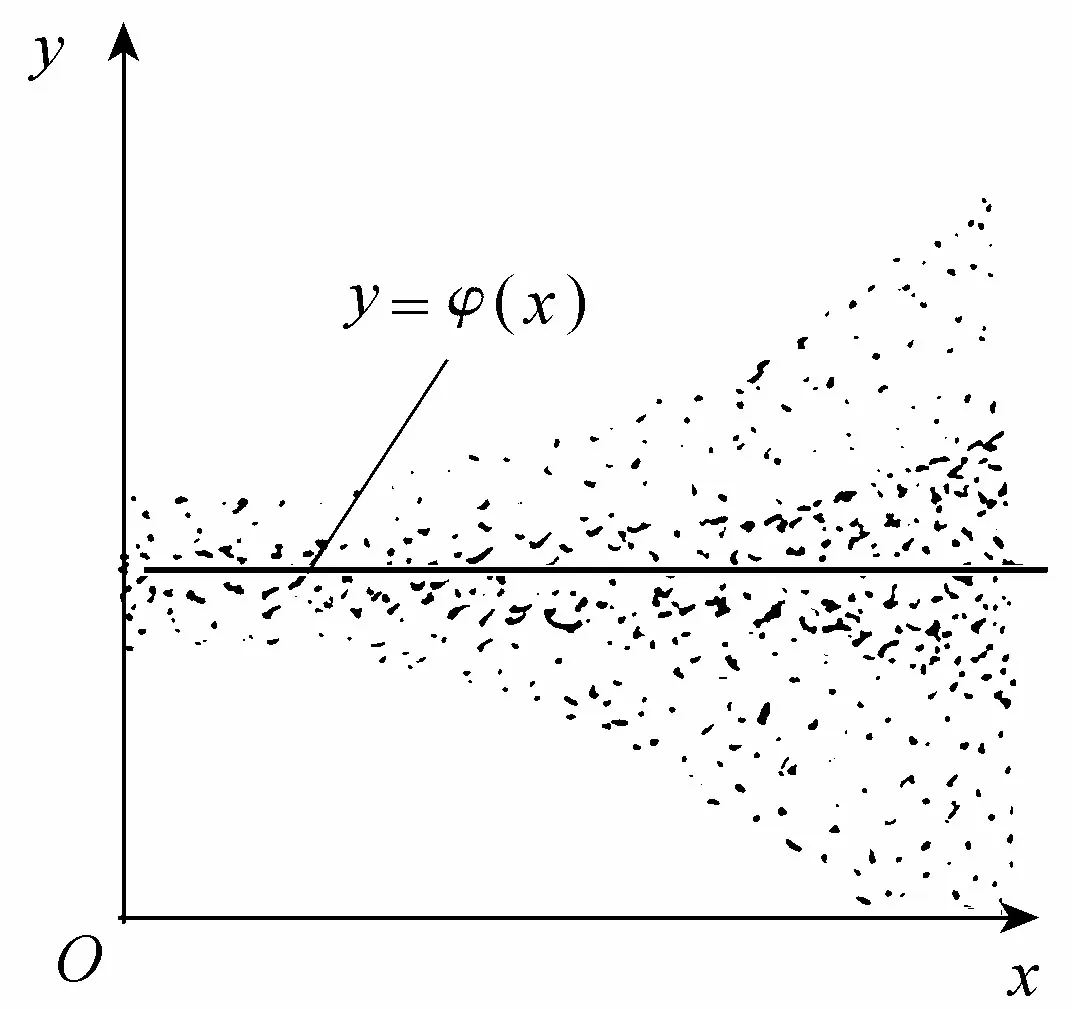
图4 弹性相关散点分布

图5 挠曲相关散点分布

利用形变函数构建两个随机变量二维分布的基本思想是；首先根据两个随机变量X与Y的相关散点图的点据分布特点识别相关类型；然后将X和Y的现实x和y经由形变函数变换成新的变量u和v，以达到消除原随机变量X与Y之间的相关性的目的 。因为两个新随机变量U和V相互独立，故可得U和V的二维密度函数和分布函数分别为f(u,v)和F(u,v)；最后通过变换再由求得的f(u,v)和F(u,v)分别得到原随机变量X与Y的二维密度函数和分布函数f(x,y)和F(u,v)。

对于刚性相关，通过下列变换就可将原随机变量X和Y转变成两个相互独立的新随机变量U和V：

u=x

(24)

(25)

式中：φ(x)为Y倚X的回归方程；(1-φ(x)/y)为刚性形变函数。

对于弹性相关，通过下列变换就可将原随机变量X和Y转变成两个相互独立的新随机变量U和V

u=x

(26)

v=yλ(x)

(27)

式中：λ(x)为弹性形变函数。

一般地，对于挠曲相关，则通过变换：

u=x

(28)

(29)

就可将原随机X和Y转变成两个相互独立的新随机变量U和V。式(29)中之λ(x)[1-φ(x)/y]称为挠曲形变函数。

由上述可知，根据形变函数理论构建刚性相关、弹性相关和挠曲相关的二维分布需要解决的问题有：寻找合适的弹性形变函数、检验新随机变量U和V的独立性、导出原随机变量与新随机变量的二维分布函数或密度函数的数学关系等。寻找合适的形变函数，至今尚无理论方法，一般只能根据相关散点图的点据分布特点，用经验试错法确定。本文仅就后两个问题做进一步讨论。

在概率论中，检验两个随机变量之间独立性的最严格方法是它们的二维分布函数等于两个边际分布函数的乘积，或者是它们的二维密度函数等于两个边际密度函数的乘积。若对两个具有相关关系的随机变量X和Y已经获得了n个二维现实：(x1，x1)、(x2，x2)、(x3，x3)、…、(xn，xn),这n个二维现实实际上就是一个来自其总体的二维样本。按照数理统计理论，利用这个二维样本可以对总体的二维分布函数和两个边际分布作出估计，事实上有F(xi,yi)=P{x≥xi∩y≥yi},F(xi)=P{X≥xi},F(yi)=P{Y≥yi}(i=1,2,…,n)。因此，如果

P{X≥xi∩Y≥yi}=P{X≥xi}·P{Y≥yi}

(30)

那么X与Y将是相互独立的。图6是利用式(30)检验两个随机变量独立性的一个实例，图中点据“×”为原变量的计算结果，点据“•”则为由形变变函数转换成新变量的计算结果。不难看出，对于两个具有相关性的随机变量，引入适当的形变函数可使它们的相关性减弱，甚至消除，从而使两个新随机变量相互独立。

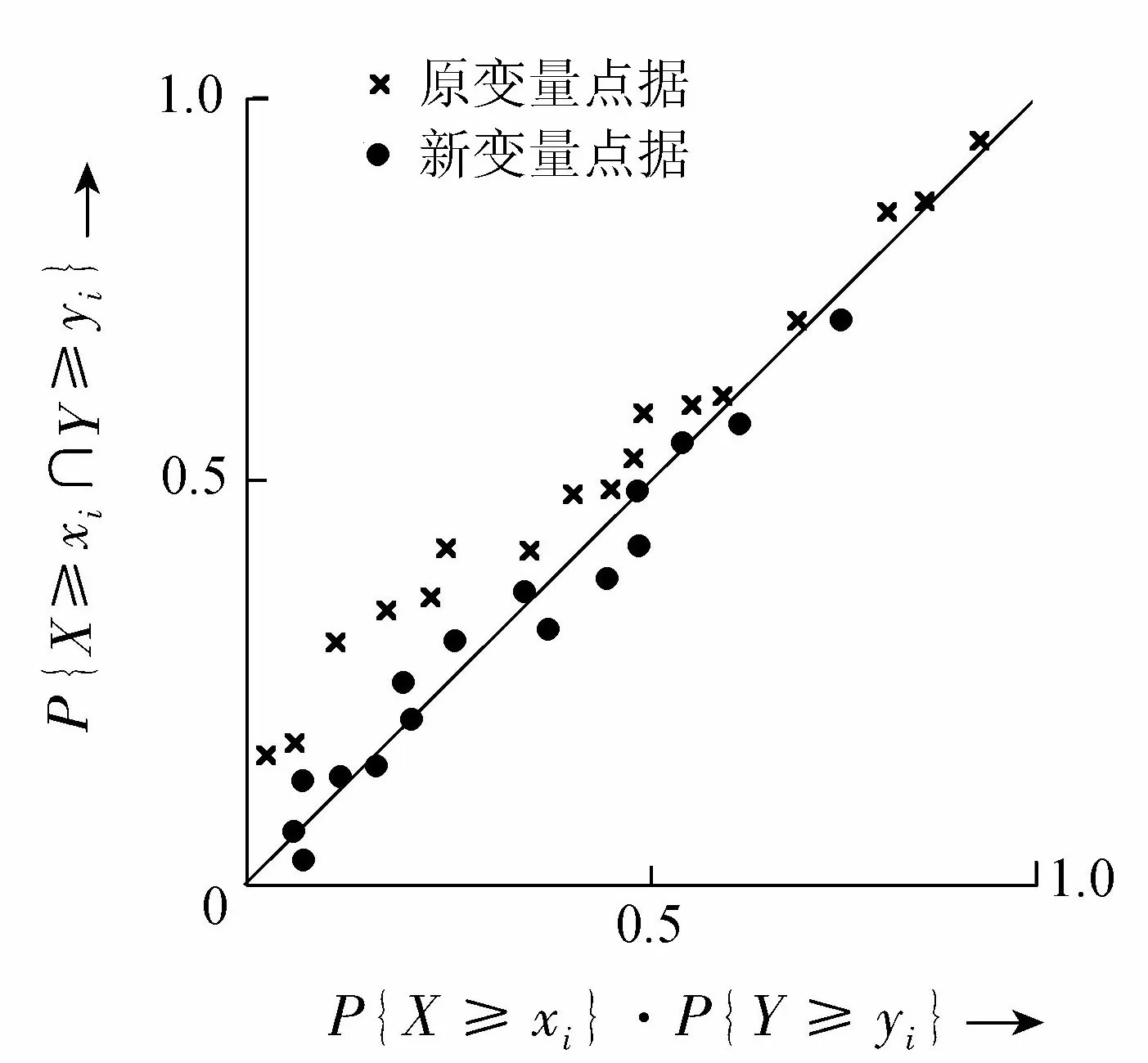
图6 独立性检验

为了导出原随机变量与新随变量二维分布函数之间的数学关系，只需利用重积分知识，即有

(31)

式中：J为雅可比行列式，其计算式为

(32)

例如：对于刚性相关，可以通过式(24)和式(25)表达的变换来使新随机变量相互独立的，因此其雅可比行列应为

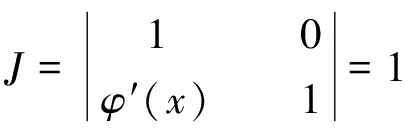
(33)

这就表明，对于刚性相关，式(31)变为

因为已证明U与V相互独立，故上式变为

(34)

同理可得弹性相关和挠曲相关情况下原随机变量与新随机变量二维分布函数之间的数学关系。

5 在水文学中的应用

在求解众多的水文学科学和应用问题时，常常会遇到求解边际分布、条件分布、复杂事件概率、随机变数函数的分布等问题。求边际分布指的是在具有相关性的两个变量中，由一个变量X的分布函数推求另一个变量Y的分布函数。由概率论知，这个问题可表达为

(35)

求条件分布指的是：在具有相关性的两个随机变量中，当其中一个X取现实x时求另一个Y的分布函数。由概率论知，这个问题可表达为

(36)

求复杂事件概率指的是推求包括有两个或两个以上随机变量的复杂随机事件的概率。由概率论知，构成复杂事件有“或”和“交”两种基本类型。因此，若复杂事件仅涉及两个随机变量，则其“或”和“交”的概率分别为

P{X≥x∪Y≥y}=P{X≥x}+P{Y≥y}-

P{X≥x∩Y≥y}=Fx(x)+Fy(y)-F(x,y)

(37)

P{X≥x∩Y≥y}=F(x,y)

(38)

求随机变量函数的分布函数指的是，当随机变量Z是另外一些随机变量X1、X2、…的函数即X=g(X1，X2，…)时，通过X1、X2、…的联合分布函数推求Z的分布函数。由概率论知，有

(39)

若Z仅是两上随机变量X和Y的函数即Z=g(X,Y)，则式(39)变为

(40)

式中：Ω为积分域。

由式(35)～(40)容易看出，无论是求边际分布和条件分布，还是求复杂事件概率和随机变量函数的分布，都要涉及二维或多维分布问题。

在水文学中，资料的插补展延属于求边际分布问题[6]。概率水文预报属于求条件分布问题[7]。非一致性样本频率分析，有的属于求复杂事件概率问题，有的则属于求随机变量函数的分布函数问题。水工程风险率[8]、设计洪水[9-10]、干支流洪水和洪与潮遭遇组合[9,11]、地貌瞬时单位线[12-14]等一般均属于求随机变量函数的分布函数问题。因其中大多数问题可在现有的文献中找到，故本文仅对二维分布在不一致性样本频率分析中的应用作具体讨论。

用数理统计理论和方法确定随机变量分布函数的思路，是通过分析样本的统计规律来推断总体的统计规律。因此前提必然是样本必须来自同一总体，如果样本不完全来自同一整体，那么这个样本就是非一致性样本，这种不一致性样本不加区别地放在一个样本中显然是不能反映总体的统计规律的。从物理成因可知，一个样本之所以不一致，可能是形成机理上的差异，也可是受到了外因，如人类活动的干扰。由后一个原因导致的样本不一致性及其改正方法已有许多文献讨论过[15],而由前一个原因导致的样本不一致性及改正，笔者发现有一种错误的观点正在流行[16]。这种错误观点认为若样本中有来自不同总体的两种信息，则其总体分布函数F(z)是这两种信息所对应的分布函数F1(x)和F2(y)分别以α和(1-α)为权重的加权平均即F(z)=αF1(x)+(1-α)F2(y)。现以某站降雨频率分析为例来说明其错误所在。由分析得知该站年最大一日雨量可能出现在梅雨季，也可能出现在台风季。也就是说，该站年最大一日雨量可能是由梅雨和台风两种天气系统形成的。如果不分形成机理而将所得年最大一日雨量系列作为样本，那么这个样本将不具备一致性。在这种情况下，正确的思维应是先分别从梅雨季和台风季中各选取最大一日雨量样本，在求得这两个样本的分布函数F1(x)和F2(y)后，再按式(4)求得该站年最大一日雨量的分布函数F(z)。因为

{Z≥z}={X≥z∪Y≥z}

所以P{Z≥z}=P{X≥z}+P{Y≥z}-

P{X≥z∩Y≥y}

即F(z)=F1(z)+F2(z)-F(z,z)

(41)

如果欲求该站年降雨量分布函数，那么由于年降雨量Z为梅雨季雨量X和台风季雨量Y之和，即Z=X+Y，而梅雨雨量和台风雨量的形成机理不同，正确的思维应是先分别建立梅雨季雨量样本和台风季雨量样本，在求得这两个样本的分布函数F(x)和F(y)后，再按下式求得年降雨量的分布函数：

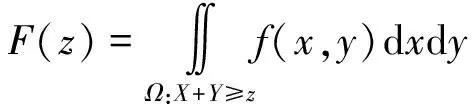
(42)

6 结 语

水文现象是十分复杂的，这不仅表现为其形成机理和时空变化十分复杂，而且表现为变量之间的关系十分复杂。对有些水文问题的解决，一维分布理论和方法已不能适应，而有待引入多维分布理论和方法。多维密度函数或多维分布函数是多维变量之间关系的最完整描述。揭示水文现象有关变量之间的关系，寻求多维分布函数，用于解决有关水文学问题已成为水文学的重要研究内容。

近一个世纪以来，无论是数学，还是水文学，对二维分布的研究都有了一些进步。在数学上提出了由两个边际分布，通过寻找连结函数构建二维分布的Copula函数理论和方法。在水文学上则发展了根据两个随机变量相关散点图的特点，通过引入形变函数构建二维分布的形变函数理论和方法。这两种理论和方法，各有千秋，如能深入研究，也许会碰撞出一些新的火花。

迄今为止，二维分布在资料插补展延、概率水文预报、非一致性频率分析、水工程风险率、设计洪水、干支流洪水及洪与潮遭遇组合、地貌瞬时单位线等水文学问题中得到了应用。笔者将二维分布处理以上问题归纳为三类：一是直接应用二维分布性质，如资料系列插补展延、概率水文预报等问题；二是通过分析事件而应用二维分布，如水工程风险率等问题；三是通过建立功能函数而应用二维分布，如设计洪水、干支流水和洪与潮遭遇组合、地貌瞬时单位线等。当然也有一些水文学问题涉及以上三类中之二，例如非一致性样本频率分析。正确应用二维分布的性质，正确分析事件之关系，以及正确选择和建立功能函数，就成为二维分布由理论通向应用的桥梁。

在水文观测年限不长，水文资料还不够丰富时，二维分布的使用必然受到很大的限制，因此在半个世纪前谈论二维分布在水文学中应用似乎过于超前，但现在面临的是信息爆炸时代，不失时机地将二维分布的研究提上议事日程，也许是当代水文学者的历史责任。