工业过程多速率分层运行优化控制
2019-11-01陆文捷马小平
代 伟 陆文捷 付 俊 马小平
先进控制与优化技术一直被认为是复杂工业过程提质增效、实现经济利润提高的关键.如今,其前沿核心技术之一是工业过程运行优化控制[1−2],内涵是采用信息技术,围绕生产过程的知识与数据信息进行集成,通过过程运行优化与控制的智能化和集成化,在保证过程安全运行的条件下,不仅使基础回路输出很好地跟踪设定值,而且控制整个运行过程,使其在生产条件约束下实现质量、效率和能耗等运行指标的最优化[3].
当前工业过程运行优化控制通常采用分层结构,其优点在于它提供了优化和控制层任务的清晰界限,在被控对象和时间尺度上均有不同.运行层面向工业运行过程,具有慢时间尺度特性,其目标是优化设定值;基础回路层面向基础设备/回路过程,具有快时间尺度特性,其目标是实现设定值的跟踪.
在工业过程运行优化控制的分层结构下,已取得了大量基于模型的研究成果,如SOC (Selfoptimizing control)以及SOC 与NCO tracking(Necessary conditions of optimality tracking)集成、RTO (Real-time optimization)以及RTO 与MPC (Model predictive control)集成的优化控制方法.
SOC 以静态经济效益模型为目标函数,离线求解一组满足生产约束的被控变量及其设定值,使工业过程受扰后,不改变设定值仍可处于近似经济最优状态[4−5].SOC 与NCO tracking 的集成方法是在SOC 选择基础回路层的被控变量后,采用NCO tracking 更新设定值,以提高动态性能[6].但对于干扰源众多或者干扰变化幅度较大的工业过程来说,难以利用SOC 确定被控变量,或者满足SOC 基本条件的被控变量根本不存在.基于RTO 的运行优化控制方法,是基于基础回路层稳态的过程模型求解运行层的最优设定值[7],但其只能在系统达到稳定时才进行优化,优化周期较长,难以处理动态扰动.基于拟稳态概念的小周期采样的RTO 方法[8]由于时间尺度难以把握,有时会导致生产不可控制的问题,难以工业应用.RTO 与MPC 的集成方法[9−11]在基础回路层采用MPC 方法,运行层采用RTO 求解期望的稳态最优值,并设计运行层MPC计算基础回路层的被控变量和MPC 输入量的设定值,上层MPC 优化与底层MPC 控制采用相同的周期,实现扰动产生后设定值的快速调整.但RTO与MPC 的集成方法存在运行层稳态模型和基础回路层动态模型失配以及网络问题,影响优化效果,为此,运行层采用过程动态模型的DRTO (Dynamic RTO)与MPC 的集成方法[12]、双层MPC 方法[13]以及RTO 与Network-based MPC 的集成方法[14]被相继提出.但实际工业过程,如冶金、选矿,运行过程机理复杂,加之设备状况及生产环境的变化影响,导致数学模型难以精确建立[1−2],从而制约了上述基于模型的分层运行优化控制方法的实际工业应用.
知识驱动的分层运行优化控制方法在假设基础回路控制器可保证设定值快速跟踪的条件下,集中研究基于专家系统[15]、案例推理[16]、模糊规则推理技术[17]及各种技术相集成[18]的运行层智能设定值优化方法.知识驱动的优化控制方法主要是依靠模拟领域专家的经验与知识,与环境的交互能力差,当工况变化时,常常依然需要领域专家对控制器进行调整,而人的主观性和随意性导致系统难以优化运行.实际工业生产过程中存在大量能够反映过程运行机理和运行状态的实时与历史运行数据,因此采用数据驱动技术来研究分层运行优化控制方法已成为当前的热点.
自适应评价设计(Adaptive critic design,ACD)是强化学习在控制理论领域中的一种近似方法,被广泛用于解决模型未知的最优控制问题[19].与ACD 相类似的名称还包括自适应动态规划[20]、神经动态规划[21]等.文献[22]借鉴ACD 思想,在假设基础回路层稳定跟踪的基础上,在运行层提出了由评价网络和执行网络串联组成的数据驱动控制回路设定值优化方法.文献[23]针对磨矿特性,提出强化学习与传统PI 集成的分层运行优化控制方法.文献[24]在基础回路层采用多回路PI 控制的基础上,提出一种基于Q-学习的次优设定值设计方法.文献[25]提出一种零和博弈脱策强化学习与传统PI 相集成的分层运行优化控制.上述分层优化控制方法考虑了两层快慢时间尺度特性,实现了设定值的动态调整.然而,实际工业过程控制系统中,因各检测装置的采样周期不同,使得基础回路层的采样和控制周期可能不同,即基础回路层也存在多速率问题,因此,工业过程的运行优化控制是具有三种及以上速率的多速率分层结构,导致上述算法难以直接使用.
本文结合工业过程分层控制结构下的多速率特点,针对一类基础回路层模型已知,运行层模型未知的工业过程,提出一种基于Q-学习、MPC 与提升技术的集成运行优化控制方法.其首先在基础回路层采用提升技术对采样与控制周期不一致的动态模型提升至框架周期,对增维后的动态模型采用MPC进行控制器设计;其次,运行层采用一种数据驱动的Q-学习方法,借助工业过程中采集的数据优化基础回路层的设定值,从而实现运行优化控制的目标;最后以闭路磨矿为背景进行实验研究,验证了方法的有效性.
1 分层运行优化控制问题描述
本部分首先简要介绍工业过程运行优化控制的层级架构,然后对多速率分层运行优化控制问题及难点进行分析,并给出本文的控制策略.
1.1 工业过程分层运行优化控制架构分析
工业过程分层运行优化控制结构如图1 所示.其中r表示工业过程运行指标,分层控制的目标即是能够通过选取一个合适的基础回路设定值w,并通过调节基础回路控制量u使回路输出y跟踪w,从而控制实际运行指标r在期望运行指标r∗附近.
工业过程包括回路过程和运行过程两层动态,其运行过程往往机理复杂难以建模,且整个系统因层级功能以及所涉及的被控对象特性的差异导致层级间时间尺度各异,以及由于信号变化速率相差较大,各检测装置的采样周期不同,难以统一基础回路的控制与采样周期.由此可以看出,工业过程运行优化控制是一个多层次、多时间尺度且部分模型未知的多速率控制问题,对现有控制理论提出了挑战.如何针对多时间尺度被控对象特性,在分层的多速率控制结构下,将运行层优化与基础回路层控制相集成,模型与数据相结合,实现运行优化控制目标是本文研究的重点.
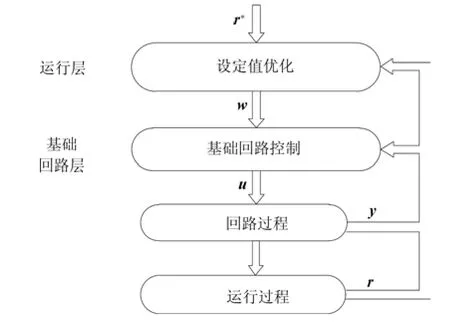
图1 多速率工业过程的双层层级架构Fig.1 Two-layer structure of multi-rate industrial processes
1.2 运行优化控制策略
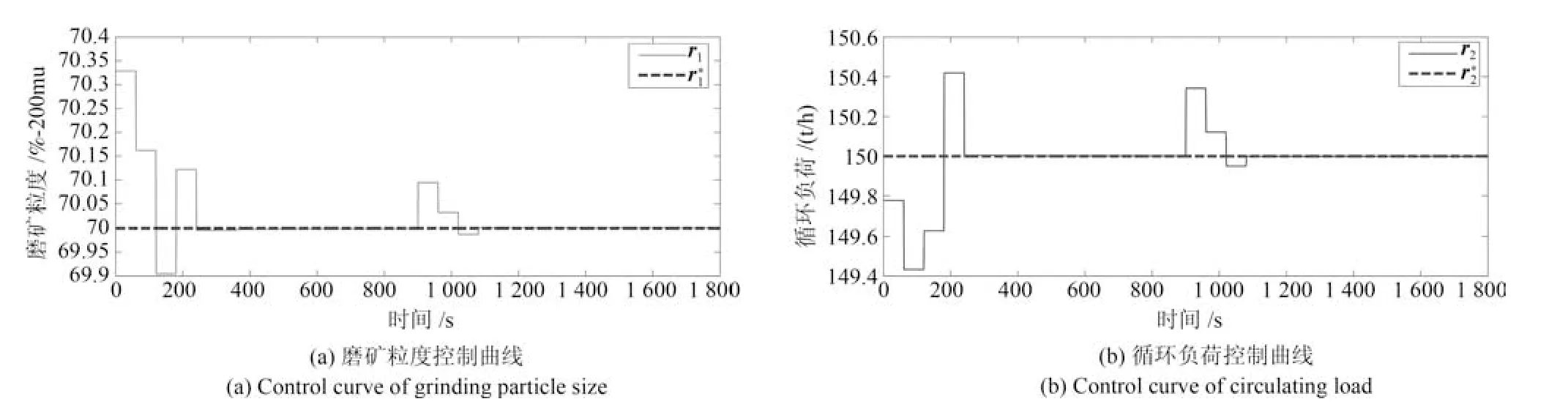
由上述分析可知,回路过程直接与检测装置以及执行机构相接触,而各种仪表因其自身的特殊性,获取信息和处理信息的速度不同,加之控制节点分散,因此在很多复杂的实际工业过程控制中,系统的控制更新速率与采样速率并不一致,且通常对控制输入的在线更新速度要求较高.因此本文考虑的基础回路层多速率采样控制策略是针对基础回路过程以T2为周期进行等周期采样,而基础回路控制器的输出由周期为T1的保持器转换得到的情况,T1与T2之间满足关系式T1 本文解决上述多速率分层运行优化控制系统设计问题的思路是:首先,通过提升技术将基础回路层的控制与采样周期均提升至框架周期T0,使该层速率一致,并采用MPC 设计基础回路控制器;然后,针对框架周期T0普遍小于运行层控制周期T(T=ξT0,ξ为正整数)的问题,进一步将基础回路层的周期T0提升至运行层控制周期T,使基础回路层的快时间尺度动态特性与运行层的慢时间尺度一致,从而构建增广状态模型用于描述由基础回路控制器、回路过程和运行过程组成的广义被控对象;继而针对这一部分模型未知的广义被控对象,提出一种基于Q-学习的数据驱动运行层设定值优化方法,以根据系统运行状态在线更新设定值. 工业实际中的回路过程往往为非线性动态模型,然而它们通常在运行点附近稳态运行,因此能在运行点附近线性化. 考虑如下连续时间基础回路过程模型: 其中,xf ∈Rnx,u ∈Rnu,y ∈Rny分别为基础回路层被控对象即回路过程的状态、控制输入和控制输出变量,nx、nu和ny表示相应变量的维数;Ac,Bc,Cc和Dc为回路过程模型的系统矩阵. 控制周期T1与采样周期T2有如下关系:T1=ph,T2=qh,p小于q且互为质数,h为基周期,由此可得框架周期T0=pqh,即T1和T2的最小公倍数.采用提升技术使基础回路层的控制与采样周期均提升至框架周期T0,以解决基础回路层中的输入输出多速率控制问题,具体方法如下. 首先以基周期h将基础回路层模型离散化为 对离散化后的系统进行提升,将输入向量维度提升q倍,输出向量维度提升p倍,即将u和y的周期均提升至T0,m表示采样周期T0下的运行步数.提升过程定义如下: 提升后的基础回路层状态空间模型如下: 为了便于表示各系统矩阵先做如下定义: 注1.对多时间尺度系统,当p和q为互质整数时,对每一个i,0≤i ≤p −1,存在整数ci ≥0 和0≤di ≤p满足iq=cip+di,i=1,2,···,p −1. 注2.经过提升后的系统(3),本质上是系统将多速率系统以“块”的思想对输入输出信号进行“堆叠”,以一个大于系统所有周期的时间为大周期即框架周期T0,对系统信息进行采集,使得输入和输出在框架周期T0内以其各自的实际周期进行增维.从而所组成的新系统方程既不损失原系统信息,又将多速率系统化为单速率,便于系统设计与分析. 提升至框架周期T0之后的基础回路层控制系统为一个多输入多输出的非方系统,且相比于原系统,不仅输入输出的维度大大增加,而且变量之间的耦合性也随之加强,难以实施常规的PID 控制方法.因此,本文采用MPC 对其进行控制.为简单起见,推导过程中的预测时域和控制时域均设置为1,具体如下. 根据式(3)可得到预测模型为 由于工业过程均为连续变化的系统,且底层基础回路控制采样与控制周期较小,通常为秒级或毫秒级,前后连续两个时刻系统变化不大,因此,为简单起见,将¯u(m+1)用¯u(m)来代替,则上式改写为 工业过程控制系统通常希望过程变量与设定值值尽可能接近外,还希望生产过程中的各类消耗尽可能低,故采用如下目标函数: 其中,α=[Iny×ny···Iny×ny]T∈RNy×ny表示将设定值w的维度提升至与相同的系数矩阵,分别为预测控制输出和控制量的加权因子,其中, 则目标函数(7)变为 将预测方程(6)代入式(8),可得: 求Jmpc的极值,即,不难得到最优控制律为 由于运行层具有慢时间尺度特性,其优化出的设定值w在运行控制周期T内保持不变,故w(m+i)=w(m),i=1,2,···,ξ −1(ξ=T/T0), 由此可得: 将式(12)代入式(3),可得系统闭环方程: 注3.将来代替只是工程上的一种近似处理方法,对于变化较快的工业过程,可计算求解两个控制时间序列即但每一时刻只实施当前的控制量. 如式(13)所示,基础回路层闭环控制周期为T0,而运行层的控制周期为T,通常情况下T >T0,此时运行层控制器的设计仍然是一个多速率控制问题,因此首先需要将系统提升到慢时间尺度T,通过递推容易得到: 则通过递归提升后的系统可以表示为 式(15)即是基础回路层在慢时间尺度T下的闭环模型,可与运行过程模型相结合构成运行层的广义被控对象. 考虑如下连续时间运行过程模型: 对式(16)按周期T进行离散化可得: 结合式(15)、式(17)两式联立得到如下增广矩阵: 由此可得,统一时间尺度后的运行层广义被控对象为 为了公式的清晰表达,在下文中多处将r(k),r∗(k),w(k),w∗(k),x(k)和XXX(k)表示为两种表示方法同义. 为实现运行指标跟踪理想运行指标r∗,定义如下性能指标: 其中,Q和R分别为半正定矩阵和正定矩阵;运行指标的期望轨迹采用类似文献[26]的处理方法,即 注4.对于跟踪问题,性能指标的前一项为了使跟踪误差足够小,保证实际运行指标能够跟踪期望值;后一项的引入是为了限定控制输入的变化程度,避免设定值过大. 注5.为保证优化控制的可实现性,还需修定性能指标,这是因为性能指标函数中包含回路设定值部分,如果当不收敛于0,而设定值w(k)由于依赖系统状态x(k)和理想运行指标r∗(k),也不收敛于0,性能指标(21)可能无界.实际工业过程中,运行指标表征工业生产中间过程的产品质量、能耗与物耗等,无法满足k →∞时收敛到0 的条件,为此,需要在性能指标函数中引入折扣因子γ(0<γ <1)避免对收敛到0 的限制,使得只要系统输入输出有界,则J有界. 结合式(20)和(21),运行层的设定值优化转化为求解如下带有折扣因子的线性二次跟踪(Linear quadratic tracking,LQT)问题. 当广义被控对象模型即式(20)已知时,可通过引入贝尔曼方程及哈密尔顿函数求解上述带有折扣因子的LQT 问题.但对于工业过程,其运行过程机理复杂难以获得模型(As,Bs,Cs,Ds),因此,式(20)含有部分未知模型,导致难以采用传统LQT 求解方法.下文首先将求解LQT 问题转化为线性二次调节(Linear quadratic regular,LQR)问题.进而引入贝尔曼方程及哈密尔顿函数进行求解,阐明该方法对系统全动态模型的依赖,继而采用增强学习,设计一种基于Q-学习的数据驱动方法. 则有折扣因子的LQT 问题(23)可重写为如下LQR: 其中,ε=C+DKx,δ=DKr −I,根据式(20)和(22)可得: 将以上两式代入式(27)中可得: 其中 则值函数表示为 由式(25)和(31),可得如下贝尔曼方程: 将式(31)代入式(32),有 由此,得到如下LQR 问题的哈密尔顿函数: 根据文献[27−28],求解LQR 问题需满足最优性的必要条件: 将式(24)代入上式,得到: 也可采用在线策略迭代算法逐步求解矩阵P和最优控制率K∗,具体算法如下: 算法1.基于贝尔曼方程的在线策略迭代算法 步骤1.策略评估(用贝尔曼方程计算Pj+1,j=1,2,···); 步骤2.策略提升 在线策略迭代算法在初始值K1能镇定系统的情况下,可通过迭代LQR 贝尔曼方程(38),采用最小二乘法(Least squares,LS)或其递推算法(Recursive least squares,RLS)计算正定矩阵Pj+1,并改进设定值优化策略直到收敛,从而获得最优的设定值. 从上述计算过程可以看出,无论是采用ARE 离线求解还是采用在线策略迭代算法,均依赖系统的全部动态信息(T,B1),对于无法建立运行过程的工业系统,两种算法均难以使用.因此,在下节中将利用Q-学习来求解带有折扣因子的LQR 问题,实现设定值优化. 基于Q-学习的设定值优化方法是一种在线迭代算法,其不需要系统动态信息(T,B1),具体算法如下: 根据贝尔曼方程(33),定义Q-函数为 由增广系统(24)可改写式(40)为 因此,定义: 由此可以看出最优设定值的求解只与矩阵H相关,类似第3.3 节中算法1 的在线策略迭代算法,本文通过在线采集的数据Xk,Zk,Zk+1对矩阵H进行逐步估计,从而求得最优设定值w∗.具体算法如下. 由于Q-函数满足如下贝尔曼方程: 将上式(44)代入式(45)可得: 根据式(43)和(46),可采用算法2 所示的在线策略迭代算法逐步求解矩阵H和最优设定值w∗. 算法2.基于Q-函数的策略迭代算法 步骤1.策略评估 步骤2.策略提升 在每一次策略评估时,矩阵Hj+1可利用数据采用LS 或RLS 获得;此后将Hj+1用于策略提升,更新后的设定值在基础回路层MPC 控制器的作用下,产生新的工业过程数据,再次用于策略评估,如此循环,当算法收敛时,通过式(48)即可求得最优设定值w∗.从上述算法过程可以看出,基于Q-学习的设定值优化方法无需任何系统动态先验知识,是一种无模型的数据驱动方法. 注6.为保证式(47)中Hj+1能够在LS 或RLS 算法下被准确估计,要求数据充分,因此在执行策略迭代时需要加入持续激励条件.实际上,工业过程在运行时不可避免会受测量扰动的影响,因此,一定程度上保证算法所需的充分持续激励条件,从而使得Hj+1能够被准确估计.从强化学习的角度看,干扰可以帮助算法更有效地探索周围的环境,增加选择最优值的几率. 注7.由式(47)可以看出,Hj+1是控制参数,本文直接采用LS 或RLS 算法对Hj+1进行估计,从而计算控制输出,不需要辨识系统模型.因此,从自适应控制的角度看,是一种直接自适应控制方法,对于具有不确定性和时变的被控对象具有一定的自学习和自适应能力. 由于V(Xk)和Q(Xk,wk)在数学公式上等价,结合式(31)和(41)可以得到: 由此可以看出Q-函数和H矩阵的同趋性,因此,当Q-函数随着j →∞而趋于最优值时,Hj和Kj都会趋于最优值,本节即通过这个思想来证明算法的收敛性. 在LS 算法充分求解,保证式(47)中Hj+1能被准确估计,且在初始控制策略保证运行指标稳定的前提下,可得引理1. 引理1. 证明.由和式(47)可得: 引理2. Kj+1和Pj+1的关系如式(39)所示,其中, 证明.式(52)可直接由式(41)得到,根据式(49)可得: 由此易得式(53). 引理3.Pj+1满足如下迭代过程: pj+1和Hj+1是同步且等价的. 证明.将引理2 中的式(52)代入式(53)可得: 定理1.假设LQR 问题在状态反馈信息下是可解的且具有一个值结构.那么,初始值H0、K0在稳定范围内时,通过定理1 中式(50)的迭代,Hj会最终趋近于H∗.其中H∗为Q-函数迭代至最优值Q∗(XXXk,wk)时的取值,此时P∗的值对应式(37)所能求出的理想解. 证明.已有文献已证明广义ARE 通过迭代可以保证初始值P0=0 时,P收敛于P∗[29],从而说明本文ARE 可通过式(55)的迭代使得Pj收敛于P∗.又引理2 和3 说明了Pj和Hj是同步变化的,所以Hj最终也会趋近于期望值H∗,即 上述算法的收敛性分析是在LS 可充分求解的前提下讨论的,对于采用RLS 算法下的控制器收敛性分析,详见文献[30]. 为了验证本文方法的有效性,本文以典型工业闭路磨矿过程为对象进行仿真实验研究. 磨矿过程是对矿石经过物理的研磨、分级处理,将颗粒由大变小,从而将有用矿物从脉石中分离出来.本文选取如图2 所示的典型磨机过程,其由电振给矿机、球磨机和水力旋流器等设备组成.磨矿生产过程中,原矿首先和一定比例的水被输送至球磨机,球磨机通过自身旋转带动机内钢球对矿石进行研磨.研磨后的矿石随矿浆流动从球磨机出口处排出流入泵池,矿浆经稀释后由底流泵打入水力旋流器进行粒度分级,形成含有细颗粒物的溢流矿浆和含有粗颗粒物的底流矿浆.底流矿浆返回至球磨机再进行研磨,形成循环负荷.由于粒度过粗或过细都不利于有用矿粒的选别,因此溢流矿浆的产品粒度r1是关键的运行指标之一;此外,循环负荷r2反映了磨矿能耗水平,是体现磨矿运行效率的重要运行指标.磨矿过程控制的目标即是实现产品粒度r1和循环负荷r2的优化控制. 由于产品粒度r1和循环负荷r2与磨机给矿量和泵池补加水密切相关,因此,磨矿系统通常设置磨机给矿和泵池补加水两个基础控制回路,运行过程以磨机给矿量和泵池补加水量为输入,以运行指标为输出.由于给矿和给水的动态过程较快,而矿石研磨需要较长的时间,因此,磨矿过程的回路过程和运行过程具有不同时间尺度特性,是一个典型的多层次、多时间尺度的控制问题.为了验证本文所提方法,将电振给矿机频率u1和泵池补水阀门开度u2两个基础控制回路的控制周期T1设置为2 s,磨机给矿量y1、和泵池补水流量y2的采样频率T2设置为3 s,运行层周期T为60 s,即ξ=10.根据本文所提的多速率分层运行优化控制方法,可以得到基周期h为1 s,框架周期即基础回路层控制周期T0为6 s. 图2 闭路磨矿过程工艺流程图Fig.2 Flow chart of closed-circuit mineral grinding process 根据文献[31],结合实际磨矿过程,两层动态模型分别采用式(49)和式(50)来近似模拟. 将上述模型转换为控制器设计所需的状态空间模型,即 由于本文方法不需要运行过程动态信息,因此运行过程模型(52)只用于被控对象仿真,其在控制器设计时并未使用. 实验设置期望的磨矿粒度为70%,期望的循环负荷为150 t/h,即r∗=[70,150]T.本文方法首先依靠系统运行产生的新数据,通过Q-学习给出新的决策量w作为给矿量和泵池补水量的设定值.然后,基础回路层通过MPC 控制器调整给矿量控制量和泵池补水量控制量,使给矿量、补水量跟踪运行层所给的设定值w. 采用本文所提方法的控制效果如图3∼5 所示,图3 描绘的是运行层磨矿粒度和循环负荷跟踪其期望值的变化曲线;图4 给出了基础回路层给矿量和泵池补水量跟踪其设定值的变化曲线;图5 是基础回路层给矿机电振频率和泵池补加水阀门开度的变化曲线. 从图3 可以看出,在运行指标初始状态与期望值较大偏离的情况下,控制系统在6 个运行控制周期即360 s 内快速实现了运行指标r的优化控制,并在每一次磨机给矿量和泵池补水流量回路的设定值w1和w2优化设定后,其过程变量y1和y2均能够在远小于运行控制周期的时间内跟踪设定值.由此可以看出,本文所提出的工业过程多速率分层运行优化控制方法在基础回路层和运行层均能够获得良好的控制效果.此外,在第900 s 仿真时间处,使模型参数发生突变,以模拟实际生产过程中矿石性质(如矿石硬度和矿石粒度)的变化对系统的扰动.从仿真结果可以看出,在出现扰动后,本文方法凭借其自身的自适应能力,可以使运行指标快速回到其期望值,具有良好的稳定性. 将所提方法与PI+MPC 和PI+PI 两种控制方法,在相同实验条件下进行对比.其中PI+MPC控制方法在运行层采用PI 控制器,控制器参数取基础回路层采用本文所提出的基于提升技术和MPC 的控制器,其控制结果如图6 和图7 所示.PI+PI控制方法在运行层和基础回路层均采用PI 控制方法以单速率设计控制器,运行层的控制器参数取;基础回路层的参数取其控制结果如图8和图9所示. 从图7 和图9 可以看出,PI+MPC 控制方法由于基础回路层采用了提升技术和MPC,基础回路层的跟踪效果好于PI+PI 控制方法,这是因为采用提升技术和MPC 设计的控制器一方面可以很好地解决多速率导致的时变特性,另一方面能够对系统的耦合进行有效的处理.由于PI+MPC 与PI+PI 两种控制方法在运行层均采用PI 控制器,因此对运行指标的控制效果相似,这可从图6 和图8 看出.虽然两种控制方法均能实现磨矿粒度和循环负荷两个运行指标的跟踪,但调节时间约1 000 s,均远远大于本文所提方法下的360 s.由此可以看出,本文所提出的工业过程多速率分层运行优化控制方法具有响应速度快,且稳定好的特点,对稳定运行指标,实现工业过程的提质增效效果显著. 图3 本文方法下的运行指标控制曲线Fig.3 Control curve of operational indices using the proposed method 图4 本文方法下的基础回路层输出曲线Fig.4 Output curve of basic loop layer using the proposed method 图5 本文方法下的基础回路层输入曲线Fig.5 Input curve of basic loop layer using the proposed method 图6 PI+MPC 方法下的运行指标控制曲线Fig.6 Control curve of operational indices using the PI+MPC method 图7 PI+MPC 方法下的基础回路层输出曲线Fig.7 Output curve of basic loop layer using the PI+MPC method 图8 PI+PI 方法下的运行指标控制曲线Fig.8 Control curve of operational indices using the PI+PI method 图9 PI+PI 方法下的基础回路层输出曲线Fig.9 Output curve of basic loop layer using the PI+PI method 本文针对多层次、多时间尺度、且运行层模型未知的复杂工业过程,创新性的考虑了多速率分层问题,将提升技术、模型预测与增强学习方法相结合,提出一种工业过程多速率分层运行优化控制方法.其通过两种提升方法将多速率分层问题统一到一个时间尺度,采用一种数据驱动的Q-学习算法,求解基础回路最优设定值,同时设计基础回路层的MPC 控制器实现设定值的快速跟踪,从而最终实现运行指标对其期望值的跟踪.将本文方法针对一段闭环磨矿过程进行了仿真实验研究,表明了其有效性.本文方法无需采用运行层模型来设计运行层控制器,仅利用数据通过自学习实现设定值的在线优化,对运行层机理复杂难以建立模型的复杂工业过程控制器的设计具有参考价值.2 基于提升技术和MPC 的基础回路层控制器设计
2.1 基于提升技术的基础回路层多速率处理方法
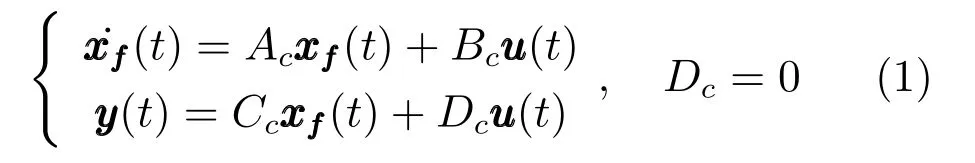

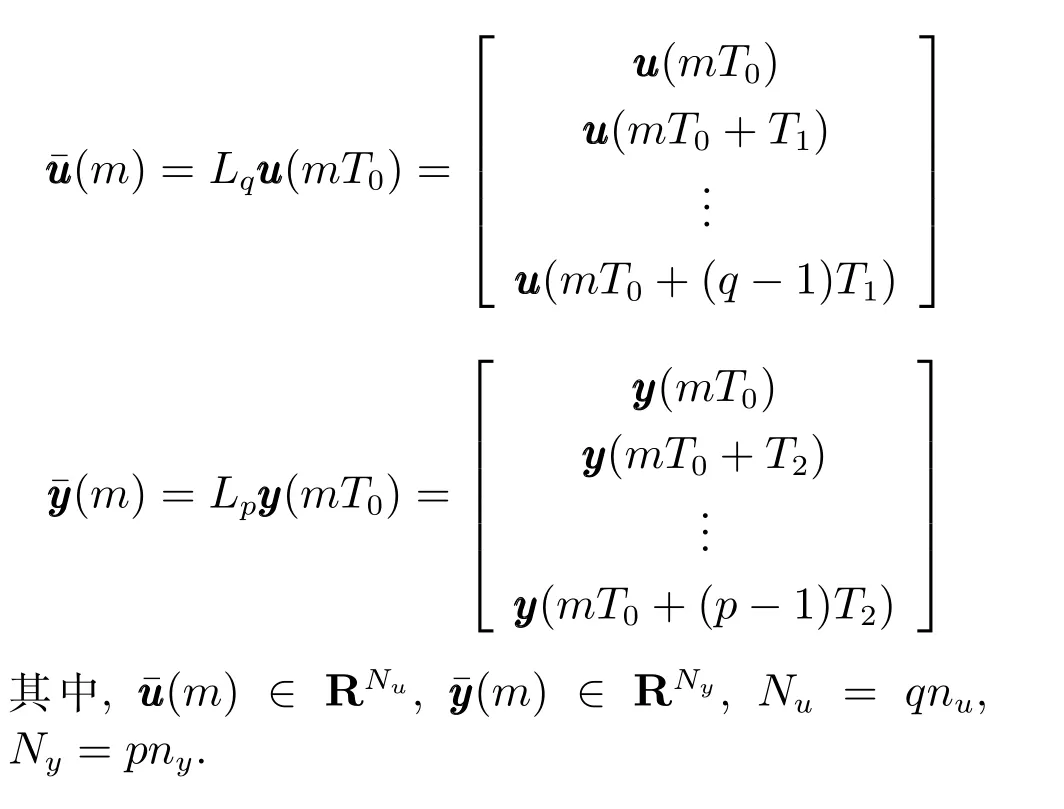
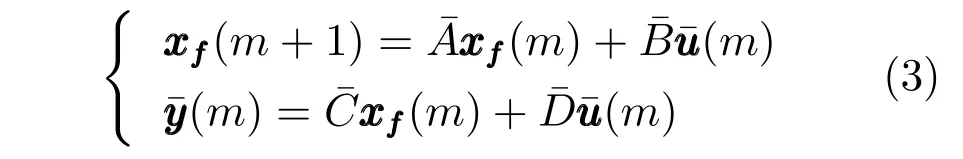

2.2 基础回路层控制器设计
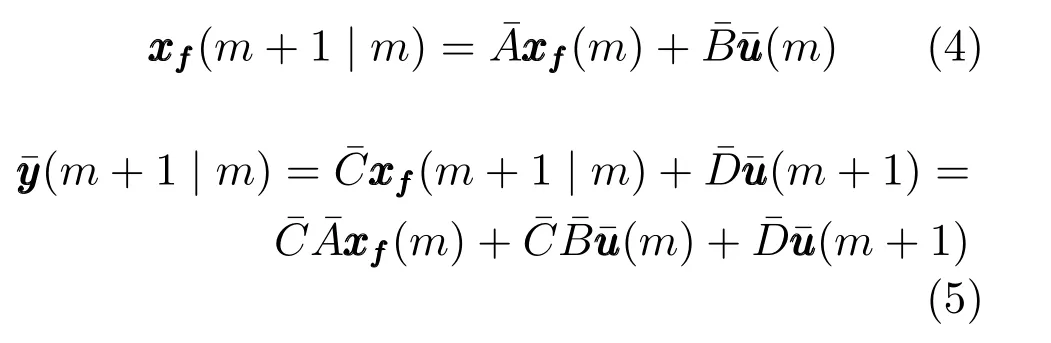



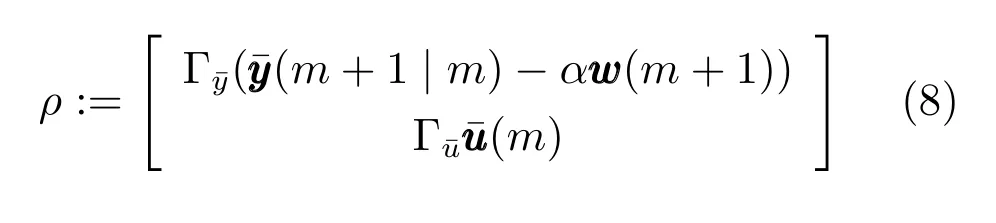
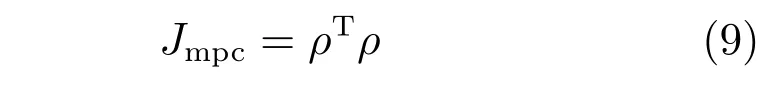
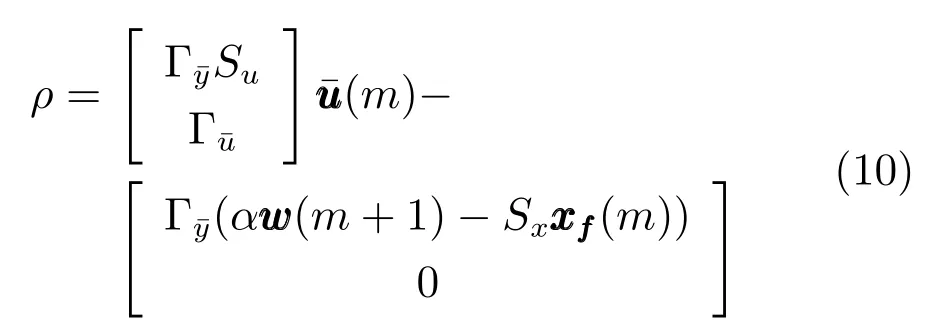
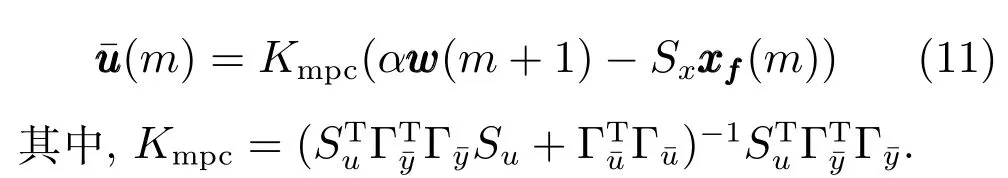
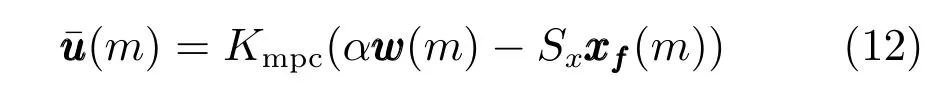
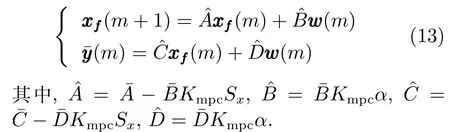
3 基于递归提升和Q-学习方法的运行层控制器设计
3.1 基于递归提升的运行层多速率处理方法
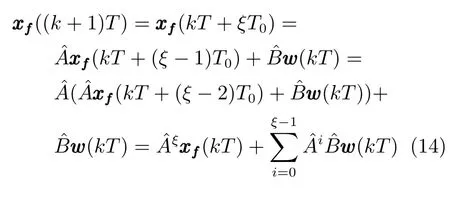
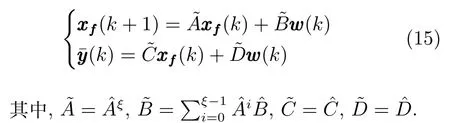
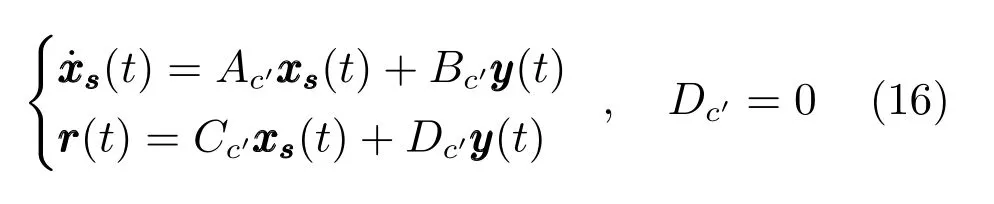
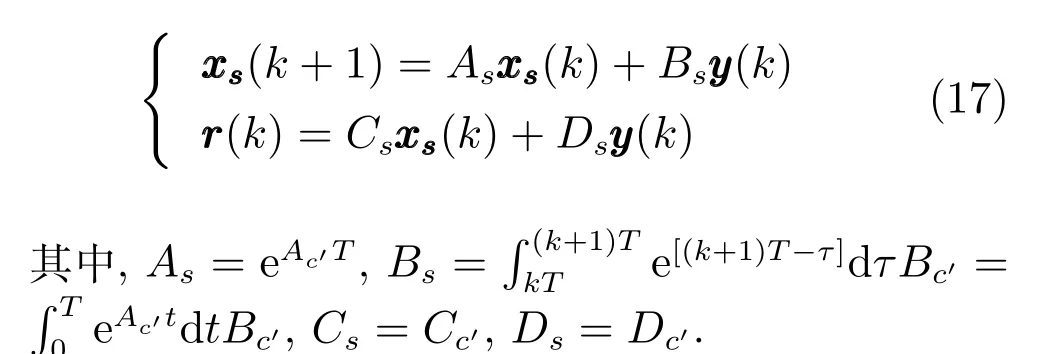
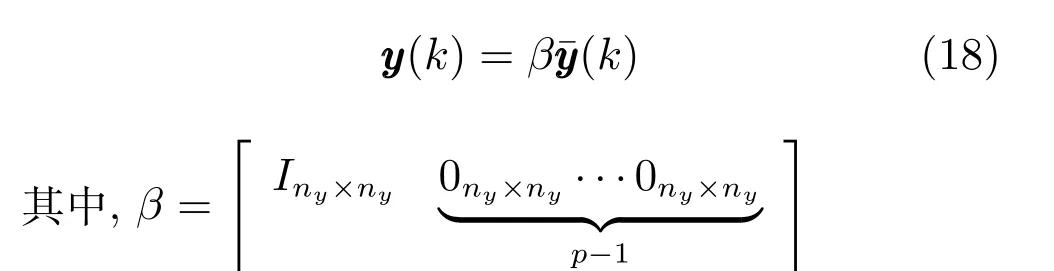
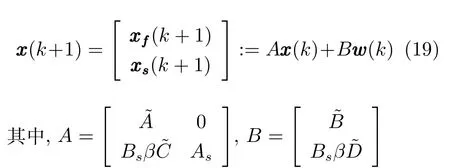
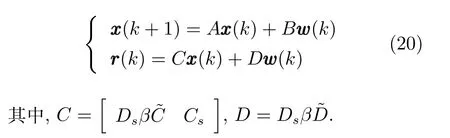
3.2 运行层设定值优化问题
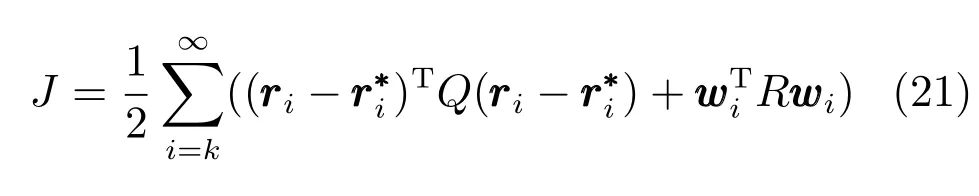
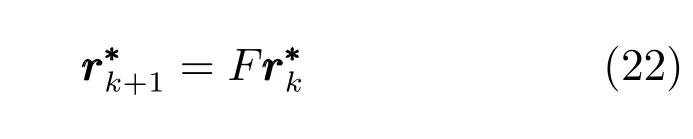
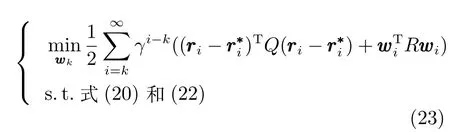
3.3 基于模型的运行层设定值优化

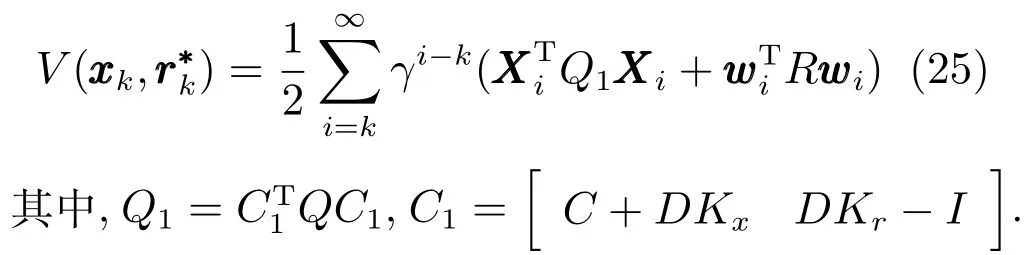
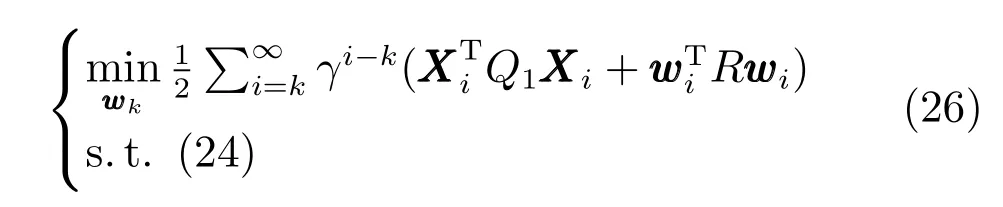
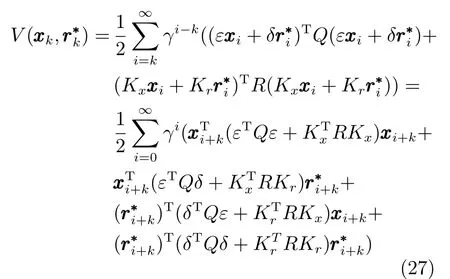
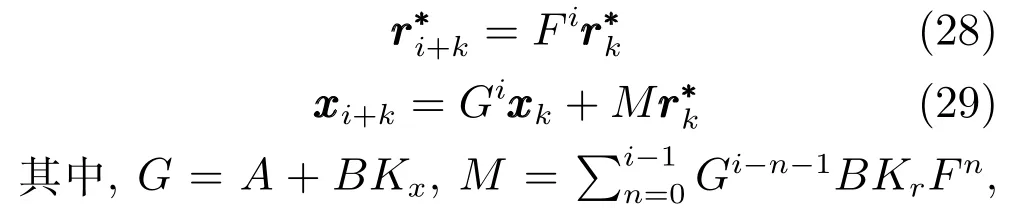
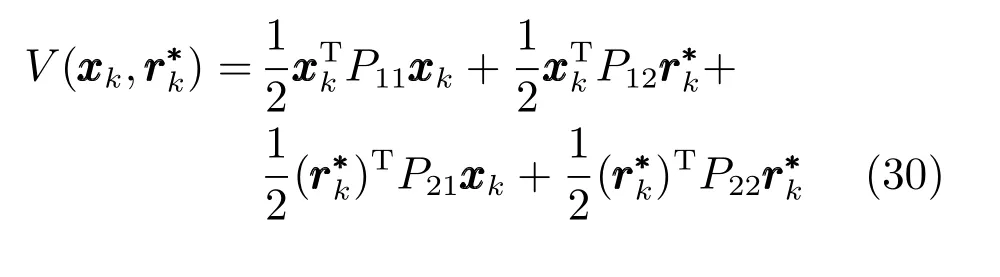
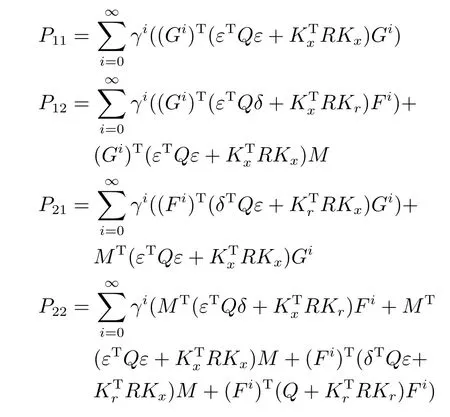
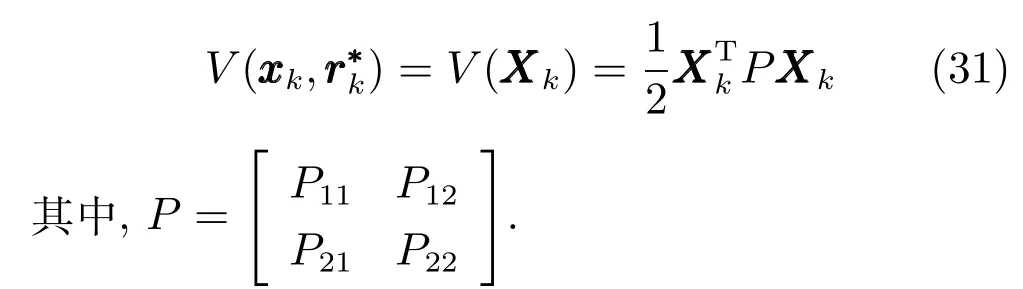
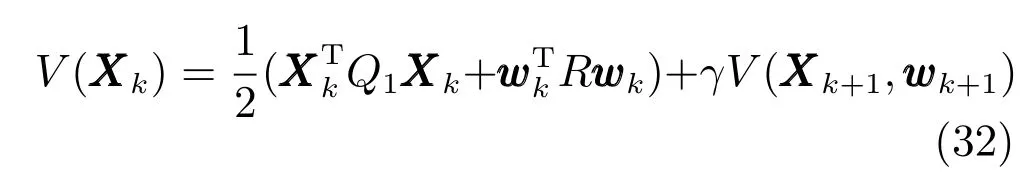
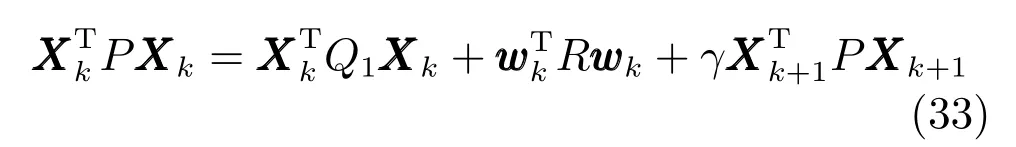
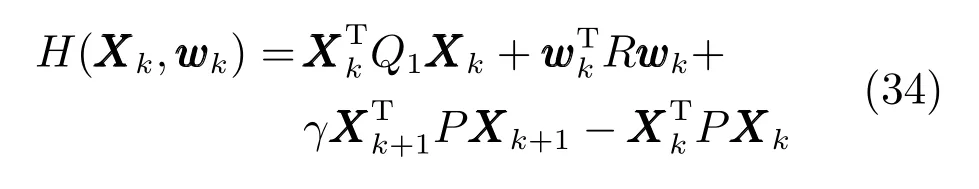
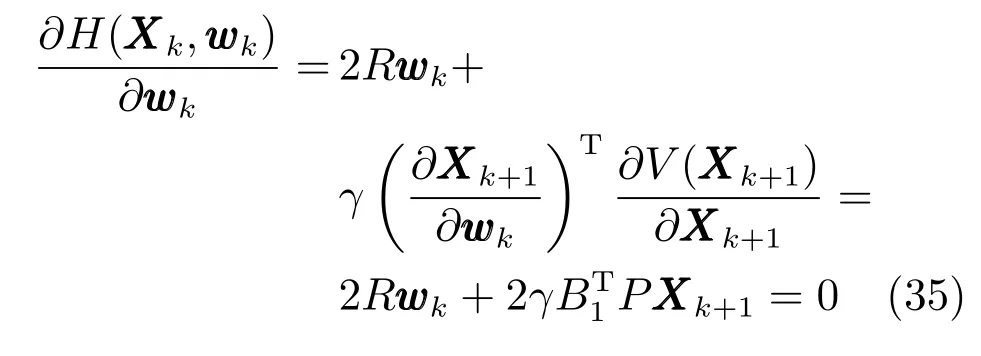

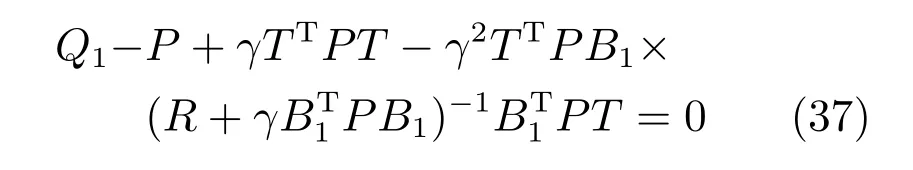
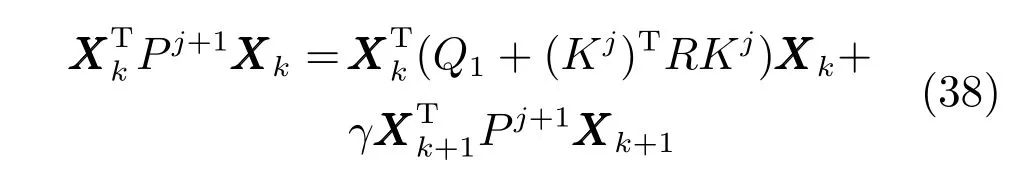
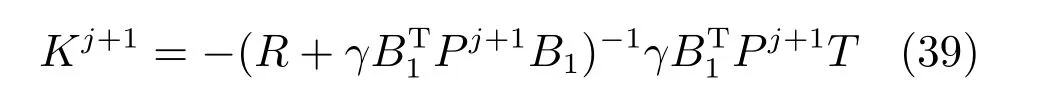
3.4 基于Q-学习的数据驱动运行层设定值优化


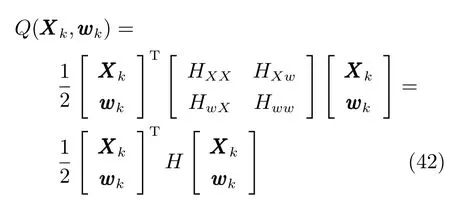
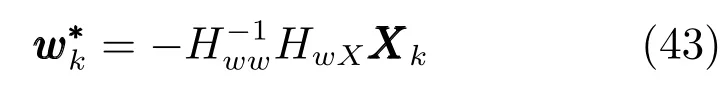
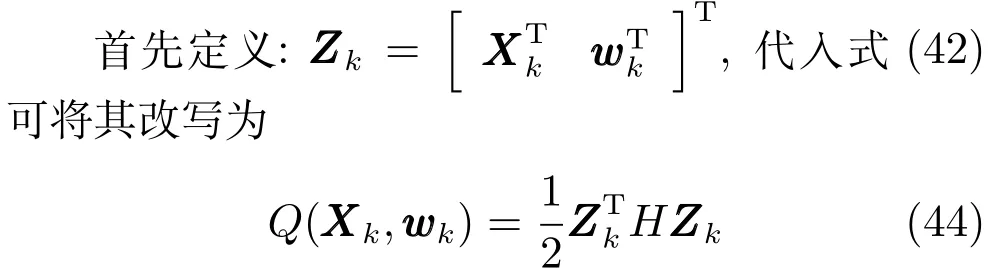
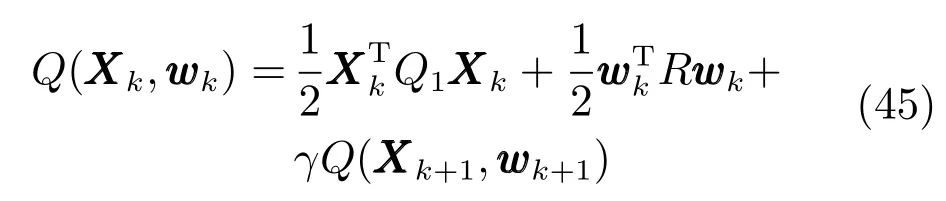
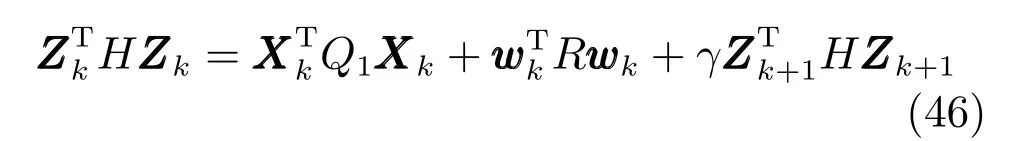
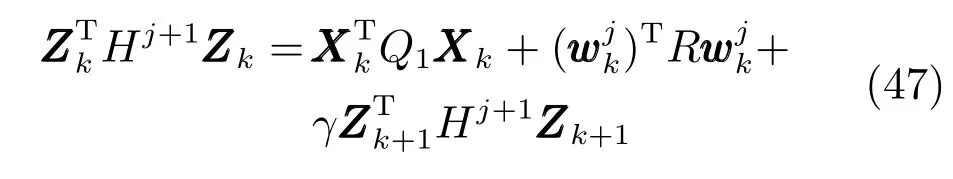
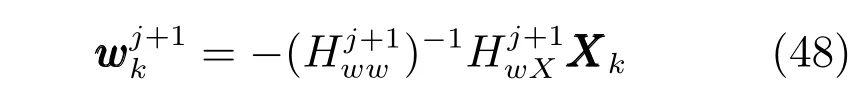
3.5 数据驱动运行层设定值优化算法的收敛性分析
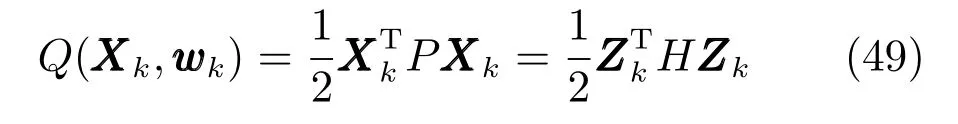
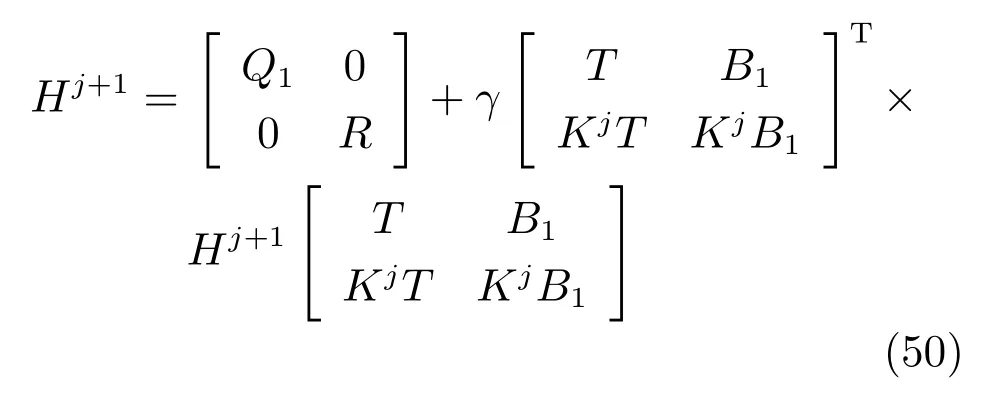
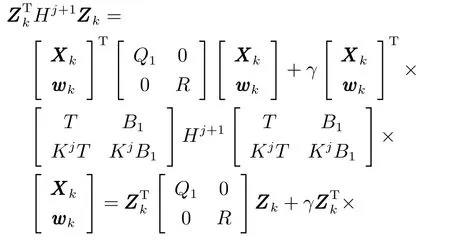
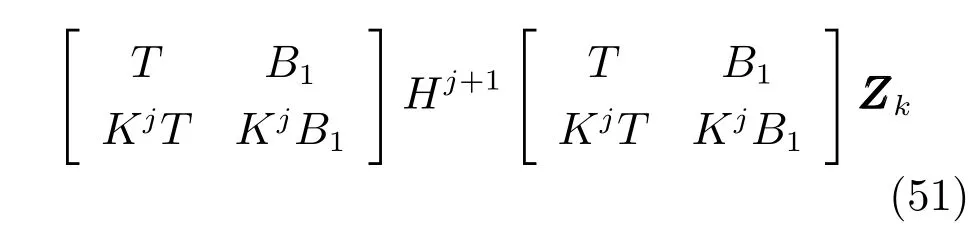
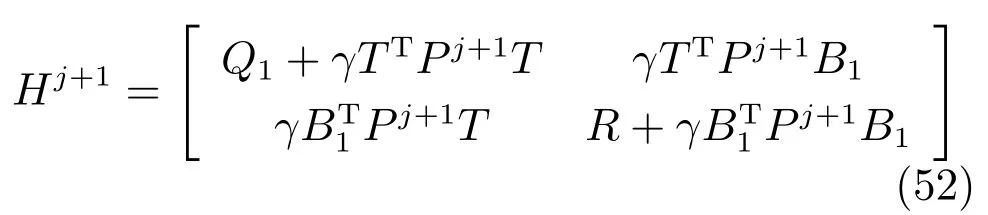

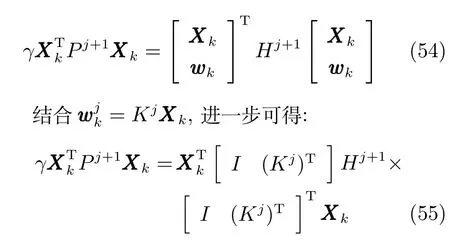
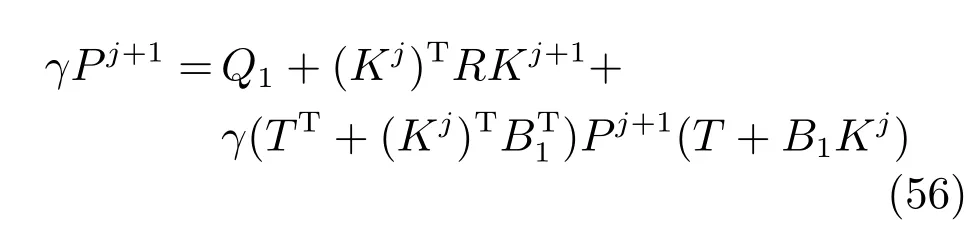
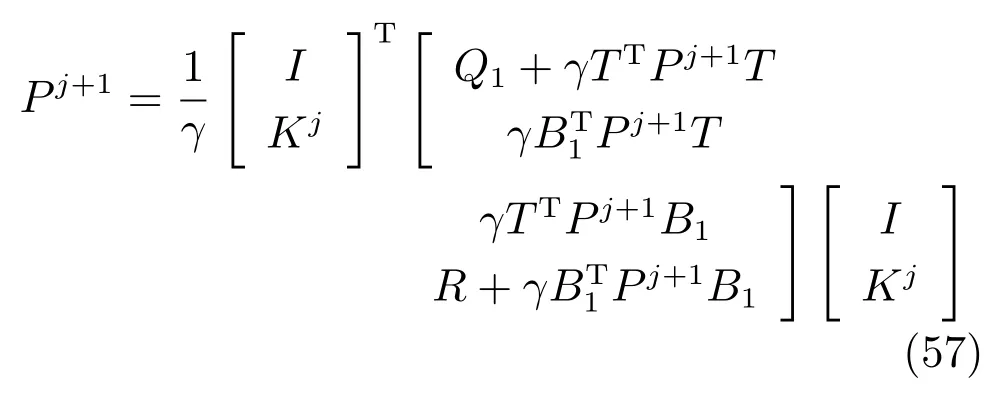
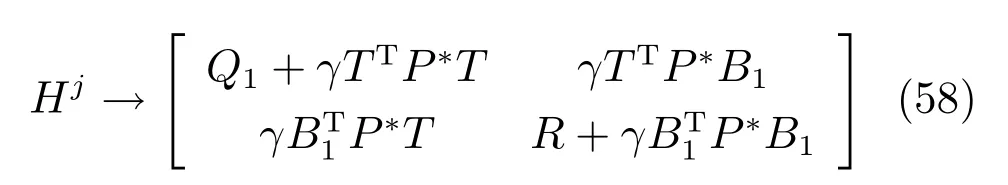
4 仿真实验
4.1 闭路磨矿工艺流程




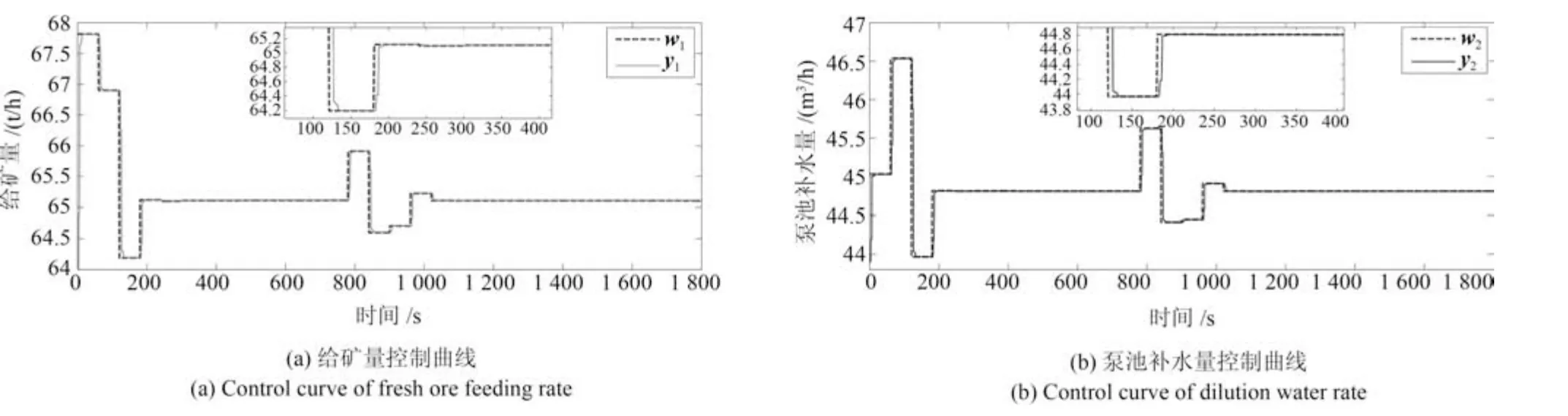
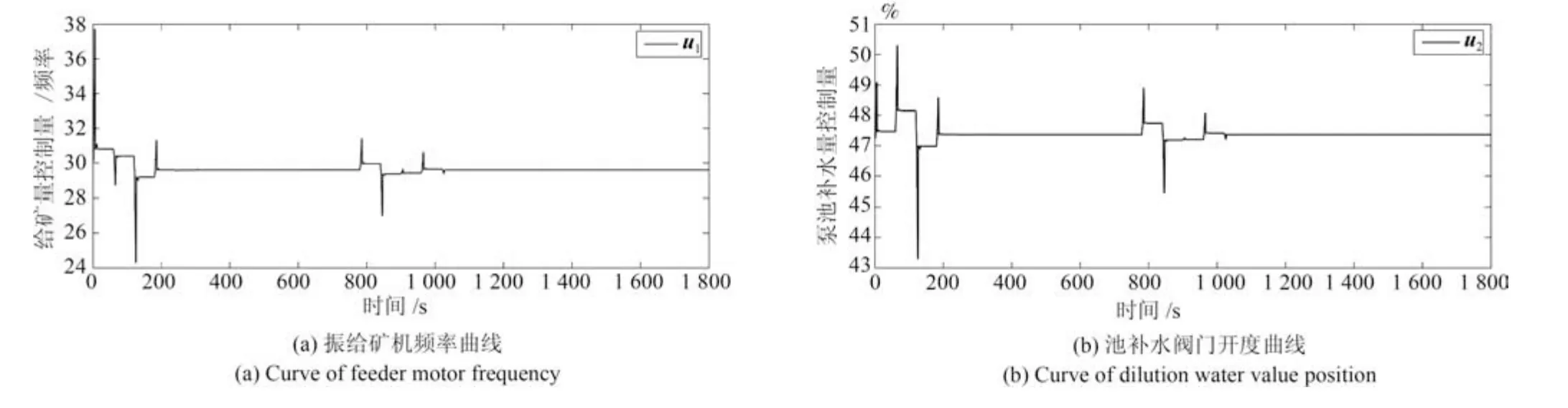
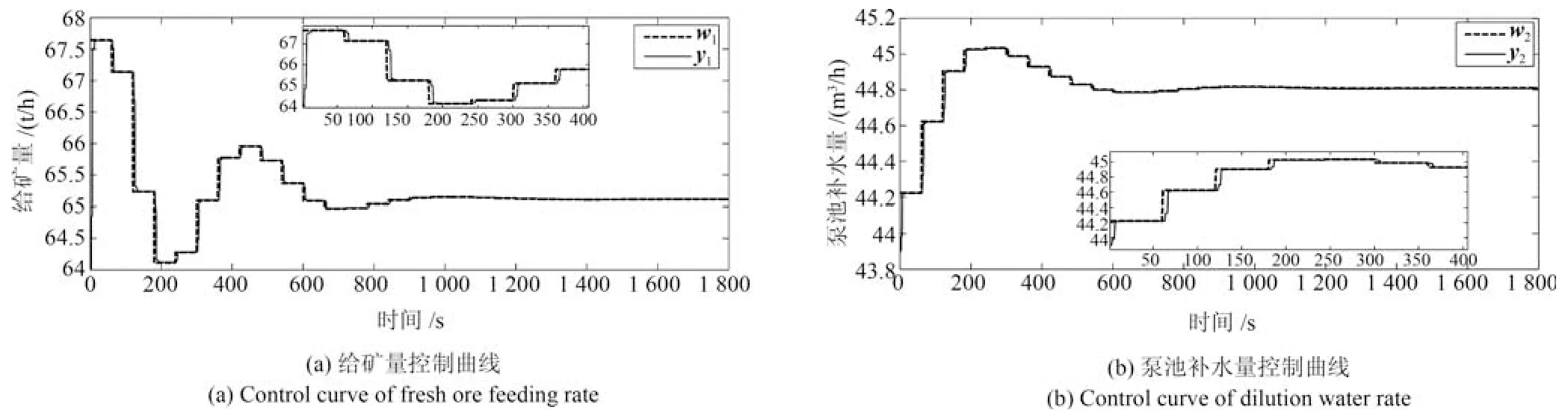
4.2 仿真实验研究



5 结论
