联合嵌入式多标签分类算法

刘慧婷 冷新杨 王利利 赵鹏

单个对象含有多个标签注释的学习与挖掘是众多领域中经常遇到和研究的问题[1−7].例如:在文本分类中,每个文档可能会被赋予几个预先定义的主题;在生物学领域中,每个基因可能会同时含有几种不同的功能片段、如新陈代谢功能、转录功能和蛋白质合成功能等;在场景图片分类中,每张场景图片从不同的角度分析会有不同含义,如人物、沙滩和天空等.这些问题都有一个共同特点,即单个实例同时含有多个标签,或被同时分为多个类别,被称为多标签问题.

近年来,多标签学习问题被众多学者关注与研究,提出了一系列的多标签学习算法.例如,基于二元相关(Binary relevance,BR)的方法[5]将多标签学习问题分割成多个独立的二元分类问题,即为每一个标签训练一个分类器;基于标签排序的方法[8−9]将标签成对比较进行排序,把多标签学习转化为标签排序问题:基于算法改编的方法[10−13]将单标签学习的算法进行改进使之适用于多标签学习.随着深度学习技术[14]的发展,文本表示能力的进一步提高,基于表示学习的多标签算法[15]被提出;此外,基于树的方法[16−17]和基于嵌入的方法[18−28]被提出用于提高多标签分类性能和减少面对高维数据时产生的昂贵的时间开销.

现存的多标签分类算法可分为两大类:问题转化法(Problem transformation methods,PTM)和算法改编法(Algorithm adaption methods,AAM).PTM 在解决多标签分类问题时,算法具有简单,易于理解与实现等优点.但PTM 缺点也比较明显,如基于二元相关的方法忽略了标签间关系:考虑到标签间的高阶相关性的标签幂集法(Label powerset)[29]因含有指数级的标签空间,不仅会导致训练时间复杂度过高,而且还可能存在标签类别的不平衡性等问题;基于链式标签法的算法[9,30],性能完全依赖于链式标签排序,但最优排序未知.AAM 通过改进已有的机器学习算法来解决多标签学习问题,如基于SVM 改进的RankSVM 算法[10−11]、基于kNN 改进的IMLLA 算法[12]及基于朴素贝叶斯改进的NBML 算法[13];这些改进型的算法避免了为每个标签单独学习而忽略了标签间的关系,当遇到具有高维特性的多标签数据时,不仅需要较大的时间消耗,性能还会有所损失.

主成分分析算法(Principal component analysis,PCA)[31]、线性判别分析(Linear discriminant analysis,LDA)[32]及局部线性嵌入(Locally linear embedding,LLE)[33]等各种嵌入技术常被用于多标签分类任务.矩阵分解技术在低维嵌入过程中可同时得到低维嵌入表示C及解码矩阵D,相比于使用PCA 及LDA 需要两个独立步骤(编码与解码),降低了误差.

为了解决PTM 与AAM 面临的问题,考虑到矩阵分解技术的优势,本文提出基于去噪自编码器(Stack denoising autoencoder,SDAE)和矩阵分解的联合嵌入学习算法Deep AE-MF,该算法不但能够得到一个具有深层语义的文本表示,还能在降低时间复杂度的同时探索标签间的关系.它能够将SDAE 对特征学习到的深层语义低维表示和矩阵分解得到的标签低维表示联合在一起共同学习,得到一个高效的多标签分类模型.与BR 型算法对比,Deep AE-MF 在学习时能够利用矩阵分解技术对标签间的关系进行间接探索;与AAM 型算法相比较,Deep AE-MF 使用SDAE 技术对特征进行了非线性学习,得到了深层语义的文本表示;与特征/标签嵌入类算法相比,Deep AE-MF 整合了SDAE 和矩阵分解两种技术对特征与标签同时进行联合嵌入学习,使得模型的预测与嵌入两个学习阶段同时进行.

在Deep AE-MF 算法中,特征部分的学习利用SDAE 能够对浅层特征挖掘出深层语义的特性得到一个深层语义的低维表示;标签部分的学习则使用矩阵分解技术得到低维嵌入表示C及解码矩阵D,避免了采用不合适的编码函数的风险同时,解决了编码与解码需要单独学习的代价;最后将特征与标签部分学习得到的低维表示联系在一起,使得特征嵌入和标签嵌入能够共同学习并得到一个共享潜在子空间用于模型的学习和预测阶段.本文主要贡献点如下:

1)Deep AE-MF 方法紧密耦合了SDAE 和矩阵分解,是一种新的基于深度学习和矩阵分解联合学习的多标签分类算法.

2)特征嵌入过程使用SDAE 能够有效地学习到数据浅层特征对应的深层语义表示.

3)Deep AE-MF 方法将特征嵌入和标签嵌入进行联合学习,能够为特征与标签空间找到一个有效的潜在共享子空间,提高多标签分类算法的泛化性能.

4)实验部分通过在6 个常用的数据集上对比10 种多标签分类算法,证明了提出的Deep AE-MF方法的有效性.

1 相关工作

随着互联网技术的普及,信息呈现指数式的爆炸增长,使得数据信息具有高维、无序及冗余等特点.例如,在一个网络社区中对某张图片进行标记注解时,其标记可能需要从百万候选标记中选择.这些高维数据的出现,使现有的基于PTM 和AAM 的多标签分类方法变的不可行[18],因为这些方法面对高维数据问题时,所需要的时间代价是不可负担的.

为了解决上述问题,文献[34]提出利用标签之间存在的依赖关系对标签构造一棵树结构用于多标签分类;文献[35]采用部分标签代替全体标签的方法.这些方法只是在一定程度上缓解了高维多标签学习存在的时间花销过高的问题.

图1 基于嵌入方法的两种模型图Fig.1 Illustration of models based on embedding method

为了更加有效地缓解高维数据带来的时间花费过大而影响算法性能的问题,维度约减/嵌入技术被用于多标签学习.维度约减/嵌入的方法大致可分为两类:基于特征的维度约减(Feature space dimension reduction,FSDR)[19−23]和基于标签的维度约减(Label space dimension reduction,LSDR)[24−28].如图1(a)所示,FSDR 首先将高维的特征空间X转化至低维潜在空间C,接着在C与Y之间学习到一个映射h(C);对未知标签实例进行预测时,先将其对应的高维特征转化为低维表示,再利用映射h(C)得到最终的预测.文献[19]在BR算法框架上对每个独立的二元分类问题学习时,使用无监督线性方式将原始特征空间转化为低维潜在空间,有效地减少了时间开销.文献[20]指出在BR框架下,每个学习问题的输入都是相同的,可通过维度约减学习得到一个共享的子空间,不仅可以减少时间开销,还解决了当标签高维时参数过多的问题.文献[19−20]均是采用线性方式对高维特征进行低维嵌入学习,但是在现实世界中,数据的高维表示与低维表示之间的关系,大都是非线性的.文献[21]则是利用非线性的核函数对原始特征进行非线性转化,文献[22−23]利用深度学习能够挖掘提取特征之间深层关系的特性,进一步对非线性关系探索,但由于只考虑到特征信息限制了模型的性能.LSDR 型嵌入学习则是针对高维的标签向量而提出的一种嵌入技术,如图1(b)所示,该方法先对高维的标签空间Y进行编码至低维潜在空间C,接着再进行学习由X与C之间的映射h(X);当对未知标签实例进行预测时,首先由映射h(X)得到低维标签表示的预测结果,然后再使用Q(解码)得到最终的预测结果.文献[24]首次采用基于标签嵌入的方法进行多标签分类,它通过对稀疏的原始标签进行探索,提出使用线性技术CS(Compress senseing)将原始标签空间转化为低维标签空间C,再利用CoSaMP 重构方法将C解码为原始标签空间表示.作为对文献[24]的进一步研究,文献[18]将标签重构过程和分类模型预测过程进行联合优化,提出基于贝叶斯框架的BLM-CS 方法用于进行多标签分类.虽然文献[18,24]能够有效地减少面对高维数据时的多标签学习的时间开销,但是在对低维标签空间C转化时未考虑标签之间存在的关系,限制了其模型的性能.于是文献[25]提出PLST 方法在原始标签空间与低维标签空间重构解码过程中使用PCA 降维技术,在对高维标签向量进行约减的同时探索到标签间的关系.文献[26]指出PLST 方法在进行维度约减时只是单纯地考虑标签信息却没有使用相关的特征信息,因此在PLST 方法基础上提出CPLST 方法,在原始标签空间重构的过程中引入相关的特征信息,进一步提高模型对未标记数据预测的准确率.文献[27]提出FaIE 方法,在对原始标签矩阵空间Y转化时使用矩阵分解技术得到低维空间表示C和解码过程Q;与PLST 和CPLST 方法使用的显式编码相比,减少不恰当使用编码函数的风险.文献[28]也是基于标签嵌入型的方法.LSDR 与FSDR 均是以找到一个合适且有效的低维表示空间为目标,因此又可统一被称为基于嵌入的方法.

由上述介绍可知,现有基于嵌入的方法中,少数工作利用核函数(如:多项式核、高斯核等)进行非线性方式转化;更少有工作在转化时同时利用特征与标签信息.因此,本文提出Deep AE-MF 方法,将模型的预测与学习过程紧密耦合共同优化学习,在联合嵌入学习过程中,不仅能够将特征的非线性表示用于标签嵌入学习过程中,还能对标签间的关系进行探索并加以利用,从而得到一个高效的多标签分类模型.

2 Deep AE-MF 算法分析与设计

2.1 基础定义

给定一个含有N个样本的数据集其中X=[x1,x2,···,xN]T∈RN×d,Y∈RN×K,X指数据集的特征空间,Y指数据集的标签空间,N是数据集中样本的个数,d是特征向量的维度,K是标签向量的维度.对于实例对(xi,yi),xi是数据集中第i个实例对应的特征向量,yi则是数据集中第i个实例对应的标签向量,当其含有第j个标签时有yij=1;否则,有yij=−1.在模型训练学习输入时统一用(xtr,ytr)表示训练实例对,测试输入时统一用(xtest,ytest)表示测试实例对,xtr和ytr分别指训练与测试时使用的实例对应的特征向量,xtest和ytest分别指训练与测试时使用的实例对应的标签向量.

定义1.多标签分类是指利用给定数据集学习到一个映射F:X →Y,当给定一个测试实例(xtest,ytest),输入xtest由映射F可正确地预测出ytest.

定义2.在多标签分类学习中,若在标签i出现的实例中,总是有标签j出现或标签j几乎都不出现,这种标签之间的共现或非共现现象被认为标签间具有相关性;前者被称作标签间正相关性,后者则是标签间负相关性.二者形式化定义分别如下:

式(1)统计的是任意两个不同的标签在数据集中的共现次数,次数越大则认为二者具有更强的正相关性(即二者具有更强的“正向依赖”关系);式(2)统计的是任意两个不同的标签在数据集中的非共现次数,次数越大则认为二者具有更强的负相关性(即二者具有更强的“负向依赖”关系).

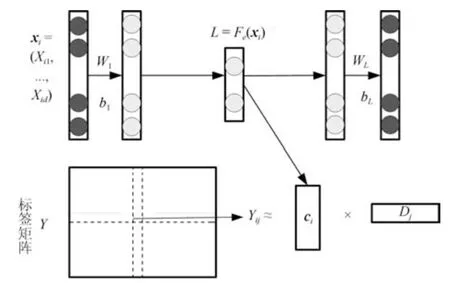
图2 Deep AE-MF 算法模型图Fig.2 The model of algorithm deep AE-MF

2.2 Deep AE-MF 方法

在标签嵌入方法的思想上结合深度学习,提出一种多标签分类方法Deep AE-MF.如图2 所示,Deep AE-MF 是基于SDAE 和矩阵分解的联合嵌入学习模型.由文献[36]可知使用SDAE 对原始特征矩阵X探索与学习,可得到一个具有深层语义的低维表示L(即Fe(X));矩阵分解则是对标签矩阵Y直接分解学习得到Y在低维空间的潜在表示C及其解码矩阵D(即Y=CDT).在训练过程中,将训练实例对(xtr,ytr)输入到Deep AE-MF 模型中,由SDAE 和矩阵分解分别得到对应的特征与标签低维空间表示,再利用CCA (Canonical correlation analysis)技术将两者对应的低维空间表示耦合在一起,使二者对应的低维潜在表示具有最大相关性,即更小的差异性,以此为模型学习到合适的潜在低维空间C.于是,Deep AE-MF 方法的目标函数如下所示:

其中,Φ1为特征嵌入学习损失,Φ2是标签嵌入学习损失,Φ3是指X与Y联合嵌入学习共同子空间损失,Φ4则是模型中参数Θ 的正则化,α、β、λ、γ则是用于平衡各种损失的超参数.

当Deep AE-MF 模型学习完成后,能够对任意输入预测其对应的标签.即在Deep AE-MF 模型中输入测试实例xtest后,首先xtest通过SDAE 中Fe编码转化为低维空间表示,接着再利用矩阵D进行解码得到最终预测结果ytest(即ytest=DFe(xtest)).下面将按照特征嵌入、标签嵌入及联合嵌入三部分详细介绍Deep AE-MF 模型.

2.2.1 特征低维嵌入学习

为了能够将高维特征空间X有效地转化至低维嵌入空间L,且更好地探索二者间的非线性关系,使用SDAE 对特征进行低维嵌入学习.SDAE 是一种以自身输入作为输出的前馈神经网络.如图2 上部分所示,SDAE 结构由5 层网络构成,以中间层为界,左边几层称之为编码层Fe,右边几层称之为解码层Fd,本文取SDAE 的中间层即Fe(X)作为X对应的低维潜在空间L的表示.为了避免过拟合,保证找到有效潜在空间L,在对SDAE 输入时加入高斯噪声ε,式(3)中Φ1即为对特征低维嵌入学习时SDAE 产生的损失,其详细形式如下所示:

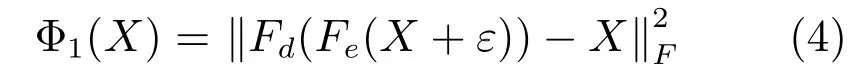
其中,X ∈RN×d是对应的未加入噪声的真实输入特征向量,ε ∈RN×d是指通过高斯分布产生的噪声矩阵,矩阵内的元素值均在0 与1 之间,X+ε ∈RN×d指加入高斯噪声后的输入,Fd(Fe(X+ε))是SDAE 的预测输出,是指傅里叶标准化(即矩阵F-范数).为了简便,除非特别说明,在下面的论述中(X+ε)均用X代替.

2.2.2 标签低维嵌入学习

如图1(b)所示,现有的大多数的标签嵌入学习包括编码P与解码Q两个独立部分,通常对于编码部分是基于某种假设得到编码函数P.但基于某种假设构造的显式编码函数可能会得到一个不恰当、不准确的低维嵌入转化,弱化了模型的性能.为了避免这种风险,本文对标签空间Y进行无假设嵌入学习—使用矩阵分解技术直接得到Y的低维嵌入表示C和对应的解码矩阵D,同时隐式地对标签之间的关系进行探索.为了提高对Y重构的能力,Y与C、D之间的差异被期望最小化,式(3)中的Φ2(Y,C,D)是对Y与C、D之间差异的描述,具体形式如下表示:

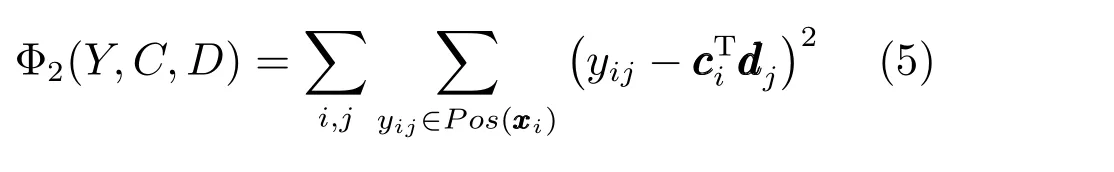
Y指标签空间,yij是指Y中第i行第j列的元素值,C=[c1,c2,···,cN]T∈RN×s是对标签嵌入学习时利用矩阵分解得到的Y对应的潜在空间表示,ci是指潜在空间表示C的第i列,D=[d1,d2,···,dK]T∈RK×s则是矩阵分解得到对C的解码矩阵,dj是指潜在空间表示D的第j列,Pos(xi)是指xi含有的标签集合.为了简便,除非特别说明,在接下来的论述中的形式均为C=[c1,c2,···,cN]T∈RN×s和D=[d1,d2,···,dK]T∈RK×s.

2.2.3 特征与标签联合嵌入学习

为了提高对低维嵌入C的可预测性,C的学习过程中应与实例的特征有着更强的相关性[37].本文使用CCA 技术将X与Y紧密耦合在一起,并使二者在低维空间具有最大相关性,以此得到一个共享潜在子空间C提高模型的性能.作为相关跨域数据(例如,输入特征数据X及其标签数据Y)的标准统计技术方法,CCA 在最大化两个域的投影空间的相关性时找到对应的投影W1及W2,即最大化corr(WT1,WT2).当使用DNN (Deep neural network)取代CCA 中对应的两个线性投影函数时,就得到了DCCA 方法.该方法能够以梯度下降法学习和更新与DNN 模型中具有类似目标函数的参数.

在本文中,Φ3(Fe,C)用于衡量特征和标签在低维潜在表示中的差异性,是标签与特征之间联系的纽带,对Φ3(Fe,C)使用CCA 技术并加入恒等约束[37],Φ3(Fe,C)有着如下的形式:

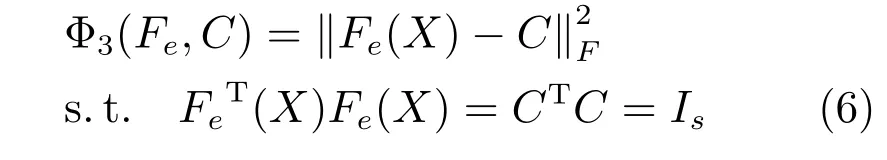
Fe指SDAE 中的编码层,Fe(X)∈RN×s是指X经过Fe得到潜在空间表示,Is ∈Rs×s是一个单位矩阵,s则是潜在空间的维度大小,C ∈RN×s是指对标签嵌入时得到的潜在空间表示.由文献[38]可知,式(6)不仅具有的功能等同于标准CCA 方法的最大化相关性功能,而且能够使用梯度下降方法有效地对参数更新.

2.3 Deep AE-MF+neg

多标签数据集中有相当一部分比例的样本含有的标签数量少于2,因此,在对Deep AE-MF 模型进行训练学习时,由于缺少丰富的标签共现信息(即标签间的正相关信息)不能对标签间的正相关信息进行有效探索与利用,限制了模型的性能;然而,这些所含标签数量少于2 的样本,却拥有着丰富非共现信息(即标签间的负相关信息).为了能够有效地利用标签间的这种负相关信息,本文在Deep AEMF 模型中引入标签负采样策略,为每个实例采样其对应的负相关标签并用于模型训练学习;关于采样的具体方案见算法1.结合式(3)∼式(6)Deep AE-MF+neg 的目标函数可表示为:

Fe和Fd分别指SDAE 中的编码层和解码层,Fe(X)∈RN×s指X经过Fe得到的低维表示,C ∈RN×s、D ∈RK×s分别指对标签嵌入时学习到的潜在空间表示与解码矩阵,矩阵是由算法1 生成.若第i个实例含有标签j或通过采样到标签j,则Mneg[i,j]=1;否则,Mneg[i,j]=0,Is ∈Rs×s是一个单位矩阵,s则是低维空间的维度大小,Φ4(Θ)表示对参数的正则化,其详细描述见式(8).

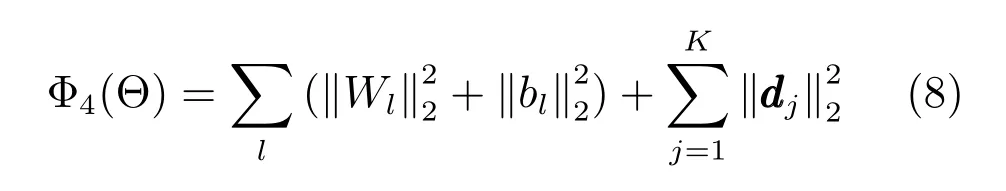
这里的Wl和bl分别指SDAE 中每层的权值矩阵和偏置,1≤l ≤5,dj为D中的第j列.同理,Deep AE-MF 的目标函数可表示成如下形式:

这里的M与式(7)中Mneg有所不同,Deep AEMF 算法在学习时未进行负采样,矩阵M中元素只与数据集的训练实例含有的标签有关,即当第i个实例含有标签j时,有M[i,j]=1;否则,M[i,j]=0.

2.4 模型优化

为了能够得到Deep AE-MF 和Deep AEMF+neg 模型,需要对式(9)与式(7)进行优化学习.由式(3)可知模型训练时的总损失表示中,Φ1(X)、Φ2(Y,C,D)、Φ3(Fe,C)、Φ4(Θ)分别是指特征低维嵌入损失,标签低维嵌入损失,子空间的学习损失,参数的正则化项.

以Deep AE-MF 为例进行优化,Deep AE-MF模型包括SDAE 和矩阵分解两个部分,对于SDAE部分的参数优化,与现有的DNN 模型优化方法一致使用梯度下降法;而对于矩阵分解部分的参数优化则采用坐标上升法.从图2 和式(9)可以看出,Φ1(X)和Φ3(Fe,C)的梯度用于SDAE 部分参数优化,Φ2(Y,C,D)和Φ3(Fe,C)的梯度则是用于矩阵分解部分的优化,Φ4(Θ)对应的是正则化项,在两部分参数更新时会有选择的使用到其对应的梯度.

对于矩阵分解部分的参数ci和dj进行优化,首先要给定SDAE 中的参数值,然后根据式(9)分别计算出参数ci和dj的梯度值,ci和dj的更新如下所示:

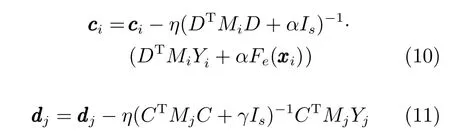
其中,Mi=diag{mi1,mi2,···,miK} ∈RK×K与Mj=diag{m1j,m2j,···,mNj} ∈RN×N分别是由矩阵M中的第i行、第j列生成的对角矩阵,矩阵M=[m1,m2,···,mN]T∈RN×K,C=[c1,c2,···,cN]T∈RN×s,D=[d1,d2,···,dK]T∈RK×s,Yi=(Yi1,Yi2,···,YiK)T∈RK×1是由标签矩阵Y的第i行组成.

关于SDAE 中参数Wl和bl更新,首先固定C和D的当前值,接着使用反向传播学习算法对SDAE 中的每层参数进行更新,每层参数更新如下所示:

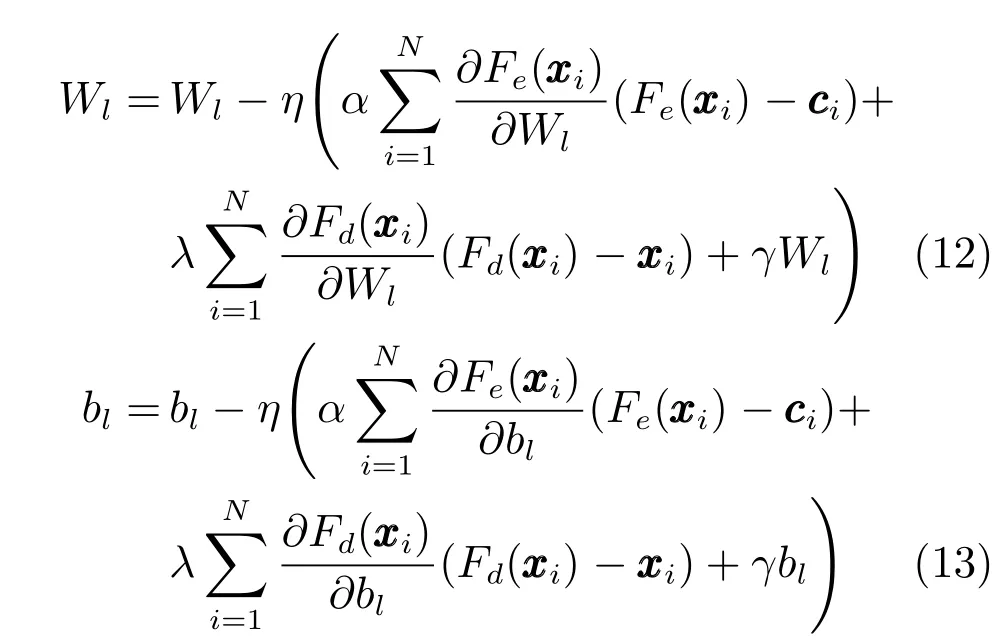
其中,Fe是指SDAE 中的编码层,Fd则是指SDAE的解码层,η是参数更新时的学习速率.

利用上述的方式对相应的参数进行更新优化,可以学习到Deep AE-MF 模型,对于Deep AEMF+neg 进行优化学习时,只需将式(10)与(11)中对应的Mi和Mj替换为Mnegi和Mnegj即可.Deep AE-MF+neg 的学习过程伪代码见算法1 与算法2.算法1 描述的是对标签进行负采样生成采样矩阵的具体过程,它利用由式(2)得到的负相关性矩阵Neg对实例含有的标签采样对应负标签,采样个数随机生成.算法2 描述的是Deep AE-MF+neg的学习过程,它的输入是特征空间X与标签空间Y及相关的超参数值.首先,在训练之前初始化模型所需的权值矩阵(步骤1);接着,由算法1 生成标签采样矩阵Mneg(步骤2);然后,由输入参数与前两步的生成结果组成所需目标函数(即式(7)),并按照式(10)∼式(13)对目标函数式(7)中的参数进行迭代更新,直至目标函数值不再变化或变化小于一定阈值(收敛)或达到最大迭代次数(步骤3).当模型学习完成后,对于任意一个的测试实例xtest,可由ytest=DFe(xtest)的方式得到对应标签预测值.

算法1.标签的负采样过程

输入.标签矩阵Y,标签数量K,样本实例数量N.

输出.标签负相关性矩阵Mneg.

步骤1.由式(2)和Y计算得到矩阵Neg ∈RK×K.

步骤2.初始化一个零矩阵Mneg∈RN×K.

步骤3.利用Y与Neg进行采样,得到Mneg

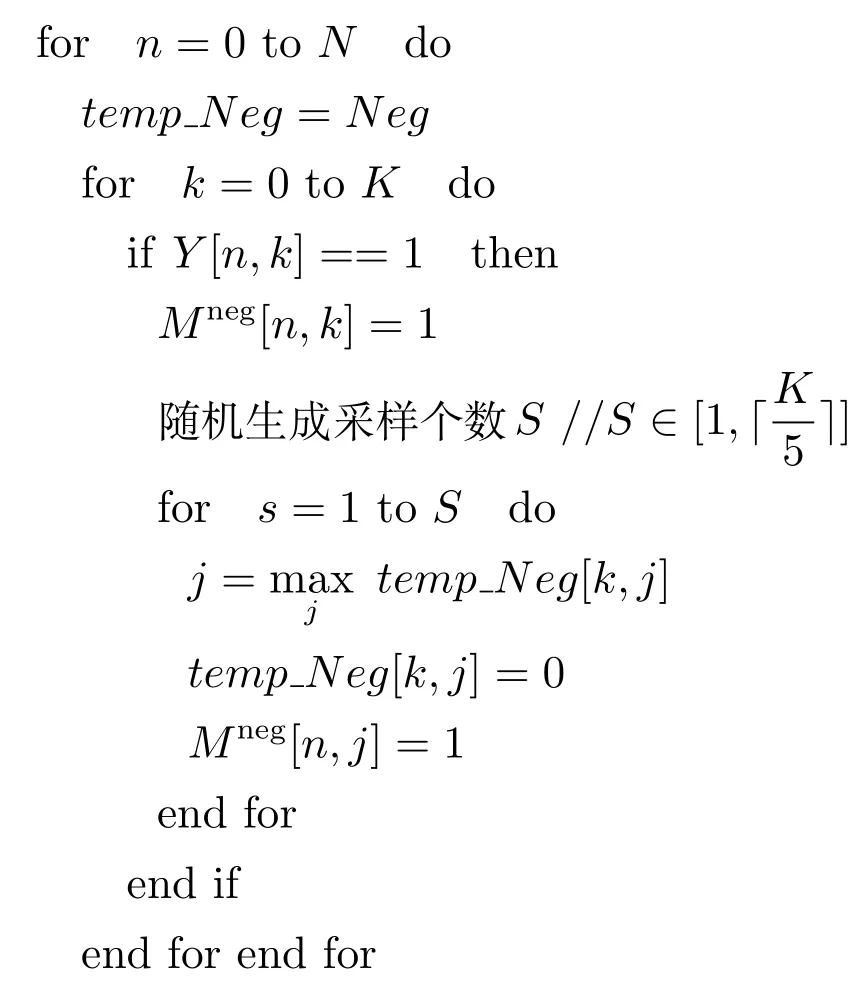
算法2.Deep AE-MF+neg 学习过程

输入.特征矩阵X,标签矩阵Y,超参数λ、α、β、γ及潜在空间大小s.

输出.Fe,Fd,D.

步骤1.随机初始化Fe,Fd,C,D,高斯分布产生一个噪声矩阵ε.

步骤2.由算法1 得到矩阵Mneg.

步骤3.重复步骤3 直至目标函数收敛(即函数值不再变化或变化小于一定的阈值)或达到最大迭代次数.

步骤3.1.按照式(7)计算出总损失,

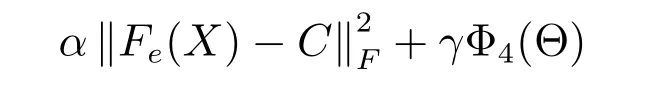
步骤3.2.按照式(10)与式(11)更新矩阵分解中的参数C与D

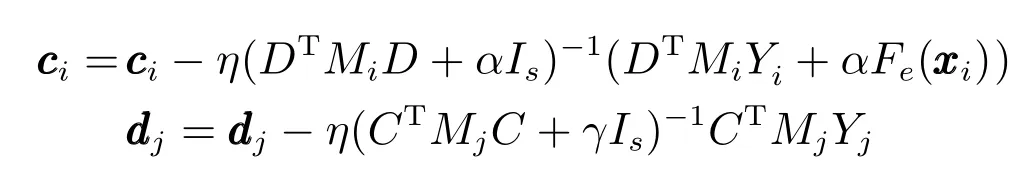
步骤3.3.按照式(12)与式(13)更新Fe,Fd

3 实验

3.1 数据集描述与预处理

为了验证本文提出的Deep AE-MF 和Deep AE-MF+neg 方法的性能,选取了6 个多标签数据集进行实验测试,分别为enron、ohsumed1http://meka.sourceforge.net/、movieLens2https://grouplens.org/datasets/movielens/、Delicious、EURLex-4K3http://manikvarma.org/downloads/XC/XMLRepository.html和TJ4http://tjzhifei.github.io/resource.html,其中前5 个是英文类型的多标签数据集,最后一个则是中文类型数据集.由于enron、ohsumed、movieLens和TJ 这4 个数据集是原始字符数据,为了能够用于实验,需要进一步对这些数据进行处理,对于英文类型的数据集进行处理时,删除数据集中的停用词、词频出现少于20 词的单词及一些非字符符号等,每个实例的特征向量表示在这里使用8 000 维的词袋进行表示;而对于中文数据集的处理,步骤与处理英文大体相同,但由于中文字词之间不像英文有空格作为分割,在预处理之前,我们首先要进行分词,分词采用通用的中文分词工具ANSJ5https://github.com/NLPchina/ansjseg.数据集更详细的描述见表1 和表2,由于EURLex-4K 和Delicious 数据集是非原始字符数据,故在表2 中无须再介绍两者的有关字符信息.

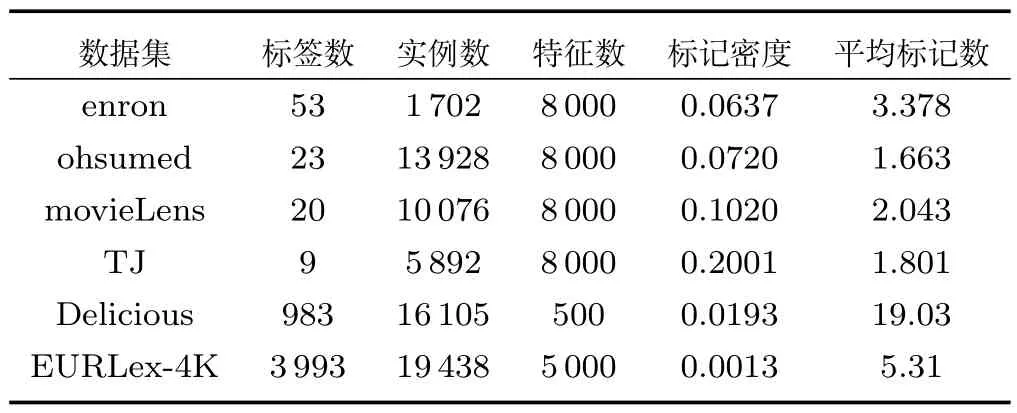
表1 多标签数据集相关统计Table 1 Multi-label datasets and associate statistics

3.2 评价准则

多标记学习框架中,每个实例可能同时拥有多个类别标签,因此,与单标签学习系统相比,多标签学习系统的评价准则相对会更加复杂些.到目前为止,已有多种评价准则被提出并广泛地用于评价多标签学习系统的性能.现选取以下5 种评价准则,即hamming loss[39]、基于标签的Macro-F1-label(或称Macro-F1)与Micro-F1-label(或称MicroF1)[40]、基于样本实例的F1 值[41]及Precision at top K (P@K)[42],用于评价多标签学习系统的性能.在这5 个评价准则中,后4 个的值越大表示模型的性能越好,最优结果值均为1;而第1 个则是值越小表示模型的性能越好,最优结果值为0.

3.3 参数设置

为了验证本文提出的方法Deep AE-MF与Deep AE-MF+neg 的有效性,将Deep AEMF 和Deep AE-MF+neg 算法与10 个多标签学习算法,即BR[5]、LS-ML[20]、CCA-SVM[20]、CCAridge[20]、PLST[25]、CPLST[26]、FaIE[27]、LEML[28]、PD-sparse[43]、和 ML-CSSP[44]进行实验比较.对比算法可分为三类:BR 代表的是经典的问题转化算法;LS-ML、CCA-SVM、CCA-ridge代表的是基于特征嵌入/约减(FSDR)型的算法:MLCSSP、PLST、CPLST、FaIE、LEML、PDsparse 则是基于标签嵌入/约减(LSDR)型的算法,其中LEML、PD-sparse 主要是针对极限多标签分类的算法.对比算法代码全部都是基于MatLab 实现的,其中BR 算法选择SVM 作为其基分类器.对LS-ML、CCA-SVM 和CCA-ridge 三个方法的参数设置均按照文献[27]最好的结果设置.对于MLCSSP、PLST、CPLST、FaIE、LEML、PDsparse 算法,超参数按照对应文献中的默认值进行设置.对于本文提出的Deep AE-MF 方法,SDAE 使用5 层的网络结构,其中学习率选取大小范围是{0.0001,0.001,0.01,0.1},对于平衡损失的超参数λ、α、β及γ设置范围则均为{0.001,0.01,0.05,0.1,0.5,1,5,10,50,100,500,1 000},潜在空间维度大小选取范围则是{0.1K,0.2K,···,K},K表示对应数据集具有的标签个数.实验结果表明:当设置损失平衡超参数λ=100,β=1,α=50,γ=0.1,s=0.6K,学习率η=0.001 时,Deep AE-MF 方法具有较好的稳定的性能.为了能够充分利用标签间的关系,Deep AE-MF+neg 模型考虑了标签间的负相关性(非共现)信息,实验结果显示利用加入的标签间的负相关性(非共现)信息能够提升模型性能.

3.4 实验结果与分析

将Deep AE-MF 和Deep AE-MF+neg 与其他10 种常见的多标签算法:BR、CCA-SVM、CCAridge、LS-ML、PLST、CPLST、MLCSSP、FaIE、LEML 和PD-sparse 进行实验比较.根据5 种评价方式,表3∼表7 分别列出了本文提出的方法与其他10 种对比算法在表1 中数据集上的详细的实验结果,且对最好的结果进行加粗表示(‘–’ 表示缺少实验结果数据).

表3 显示算法Deep AE-MF 和Deep AEMF+neg 在6 个数据集中均有4 个数据集相比于对比算法有着更小的hamming loss 值,即有着最好的性能,而且在这4 个数据集中有3 个相对于次优结果的算法分别有着3%∼10% 左右的性能提高.但二者在ohsumed 和Delicious 上排在了较差的位置,与最优结果相比有1.5% 左右的差距,从表1 的分析可以看出,ohsumed 数据集标签的平均密度相比于其他数据集过小,Delicious 数据集的特征维度偏小.在movieLens 数据中,Deep AEMF+neg 的性能略低于Deep AE-MF 性能,原因是Deep AE-MF+neg 没有像Deep AE-MF 在预测时偏好于将大部分的标签预测为−1,在数据集中标签为−1 相对1 所占的比例是非常大的,故而将标签预测为−1,可有效地减少预测错误率(即得到hamming loss 值更小).从6 个数据集中的综合结果来看,Deep AE-MF 和Deep AE-MF+neg 是优于其对比算法的.

从表4 中的结果可以看出:Deep AE-MF 和Deep AE-MF+neg 这两种方法在6 个数据集上均取得了最好的结果,优于所有的对比算法,表明SDAE 学习得到的非线性表示有利于分类模型性能的提高.其中Deep AE-MF+neg 方法好于Deep AE-MF 方法,说明通过利用标签的负相关性(非共现)信息可进一步提高模型的性能.从表4 中可看出BR 方法的性能较差,而基于嵌入方法的性能大都排在中间位置.

从表5 中的显示的结果看:Deep AEMF 和 Deep AE-MF+neg 方-法-在 movie-Lens、TJ、enron、Delicious 及EURLex-4K 这5 个数据集上取得了最好的性能,且在Delicious 和EURLex-4K 上与第3 名结果有接近10% 左右的性能提高;在ohsumed 中,基于特征嵌入的几种方法取得了比较好的结果,比Deep AE-MF 方法提高了1.5% 左右,但是在其他数据集上的性能与Deep AE-MF 和Deep AE-MF+neg 方法相比要差很多.所以,在6 个数据上进行综合性能的比较,Deep AE-MF 和Deep AE-MF+neg 方法排在前两位,采用了基于嵌入方法的算法排在中间位置,BR 最差.

表2 多标签数据集字符数量统计Table 2 The number of characters in a multi-label dataset

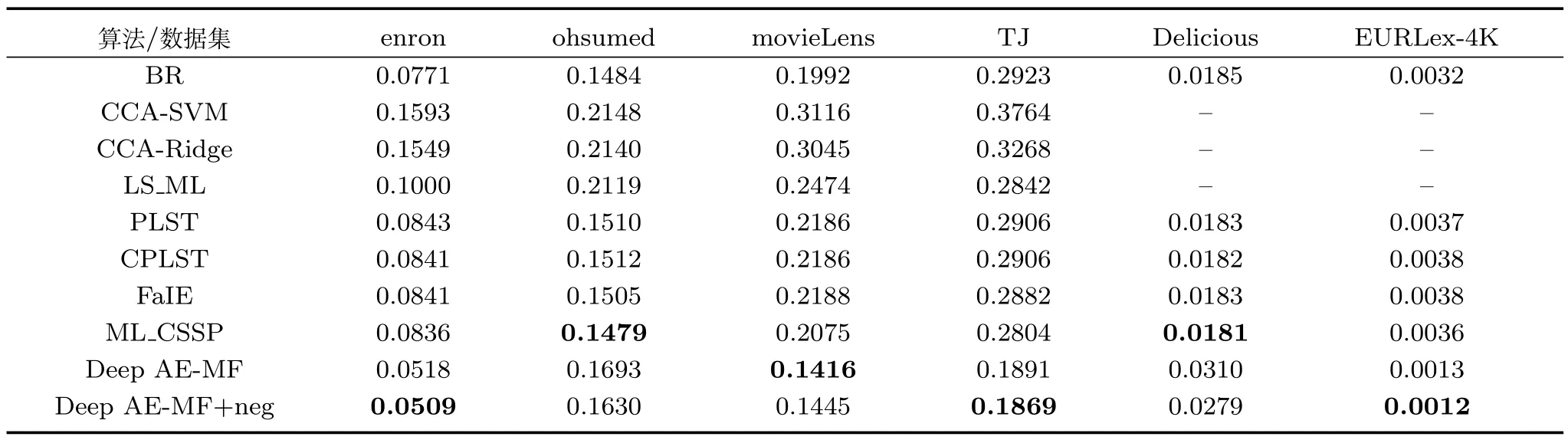
表3 基于hamming loss的性能比较Table 3 The hamming loss of ten multi-label algorithms with respect to different data sets

表4 基于Micro-F1-label 的性能比较Table 4 The Micro-F1-label of ten multi-label algorithms with respect to different data sets

表5 基于Macro-F1-label 的性能比较Table 5 The Macro-F1-label of ten multi-label algorithms with respect to different data sets

表6 基于F1 的性能比较Table 6 The F1 of ten multi-label algorithms with respect to different data sets

从表6 中的显示的结果看:Deep AE-MF 和Deep AE-MF+neg 在enron、ohsumed、Delicious及EURLex-4K 上取得了最好的结果,但在movie-Lens 数据集中Deep AE-MF 和Deep AE-MF+neg则排在次优位.原因是使用了线性与非线性转化的LS-ML 方法能够对每个实例含有的标签进行较好的预测,但与LS ML 相比本文的方法也只相差2%和1.5%.对于数据集TJ,Deep AE-MF+neg 排在了第一位置,Deep AE-MF 则排在了中间偏低的位置,原因是这些LSDR 型算法在标签维度约减的过程都直接或间接的利用了标签关系信息,与Deep AE-MF 相比能够找到一个更加有效的潜在低维标签空间.从综合性能上,Deep AE-MF 和Deep AEMF+neg 仍然领先于对比算法,尤其是BR 方法和FSDR 型的方法.

表7 基于P@K 的性能比较Table 7 The P@K of six multi-label algorithms with respect to different data sets

表7 中的数据是有关Deep AE-MF 和Deep AE-MF+neg 与极限多标签分类算法在标签数量较大的数据集中实验结果,在性能比较时,采用极限多标签分类常用的度量准则P@K (Precision at top K).实验结果显示当取不同的K值时,Deep AEMF 和Deep AE-MF+neg 均取得了最优的结果,表明了本文提出的算法能够较好解决标签维度过高的问题,且有着不错的性能.

表3∼表7 中在5 种评价标准上的实验结果显示,提出的Deep AE-MF 和Deep AE-MF+neg 的方法明显优于其对比算法.在联合嵌入学习过程中,SDAE 得到的非线性表示Fe(X),矩阵分解直接得到的低维标签表示C和解码矩阵D,有利于学习找到一个泛化能力更好的分类模型.从表中可以看出Deep AE-MF+neg 的性能几乎一直优于Deep AE-MF,表明在对标签嵌入时利用标签之间的非共现信息可以进一步提高算法的性能.

为了在统计上比较提出的算法与其对比算法在6 个数据集的实验结果,采用显著性水平为5% 的Students t test[45].在Deep AE-MF 与除Deep AE-MF+neg 外的算法对比检验时,以Deep AEMF 的性能差于或等于其对比算法的性能作为零假设,以Deep AE-MF 的性能好于其对比算法性能作为备选假设.从表8 中可以看出Deep AE-MF与每个对比算法在6 个数据集上的P值,在hamming loss 上只有一个是大于0.05 (即支持原假设);在Micro-F1-label 上所有P值均小于0.05,即均支持Deep AE-MF 的性能是好于其对比算法;在Macro-F1-label 上,仅有两个P值是大于0.05;综合分析说明Deep AE-MF 的性能优于其他算法.对于Deep AE-MF 与Deep AE-MF+neg 性能检验时,以二者性能相当作为零假设,从表8 中可以看出在3 种评价准则与6 个数据集上,18 个P值中只有2 个是大于0.05 (支持原假设),因此可认为二者的性能是有显著差异的.上述t test 的结果与分析验证本文提出算法的有效性.

3.5 参数分析

3.5.1 超参α 的敏感性分析

为了验证超参数α对Deep AE-MF 性能的影响,在{1,5,10,···,1 000}中选择不同值进行实验.本文在两个数据集上使用三种评价方式来研究参数α对实验性能的影响,结果如图3 所示.

从图3 可以看出,对于hamming loss 在enron和TJ 两个数据集上,随着α的增加,曲线先下降再升高(即性能先上升再下降);对于基于标签的Macro-F1 和Micro-F1 在enron 和TJ 两个数据集上,随着α的增加,曲线先上升再下降(即性能先上升再下降).

由图3 中可以得出α=50 附近时,在enron 和TJ 上模型均有着最佳的性能.通过分析可以认为,当α <50 时,特征和标签联合嵌入所占比重过小,使得在对标签探索嵌入时,过于注重对标签空间Y的重构,在学习标签潜在表示空间C时未能充分利用特征信息;当α >50 时,特征和标签联合嵌入时所占比重过大,表明标签嵌入时在学习标签潜在表示空间C时偏好于使用特征信息,使模型降低对标签空间Y的学习,导致对Y的重构或预测能力下降.综合对实验结果权衡分析,选取α=50 作为最终取值.

3.5.2 参数s 的敏感性分析

为找出能够使Deep AE-MF 性能最佳时的潜在空间维度s值,在{0.1K,0.2K,···,K}中选择不同s值进行实验,其中K表示数据集标签的个数.本文在两个数据集上使用三种评价方式来研究参数s对实验性能的影响,结果如图4 所示.

表8 Students t test 结果P 值(加粗表示P 值大于0.05)Table 8 P value of Students t test results (Bold indicates that P value is greater than 0.05)

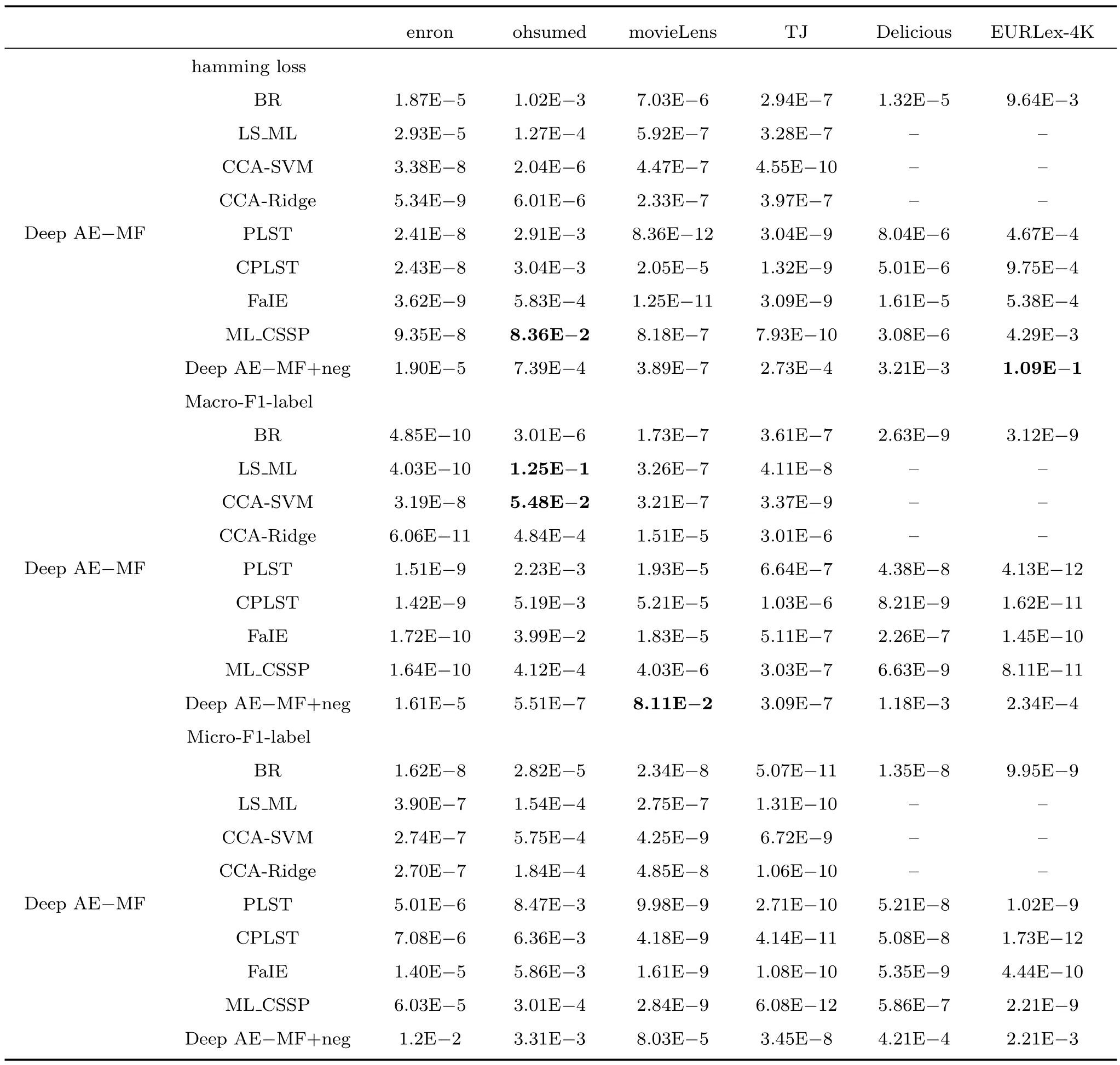
表8 Students t test 结果P 值(加粗表示P 值大于0.05)Table 8 P value of Students t test results (Bold indicates that P value is greater than 0.05)

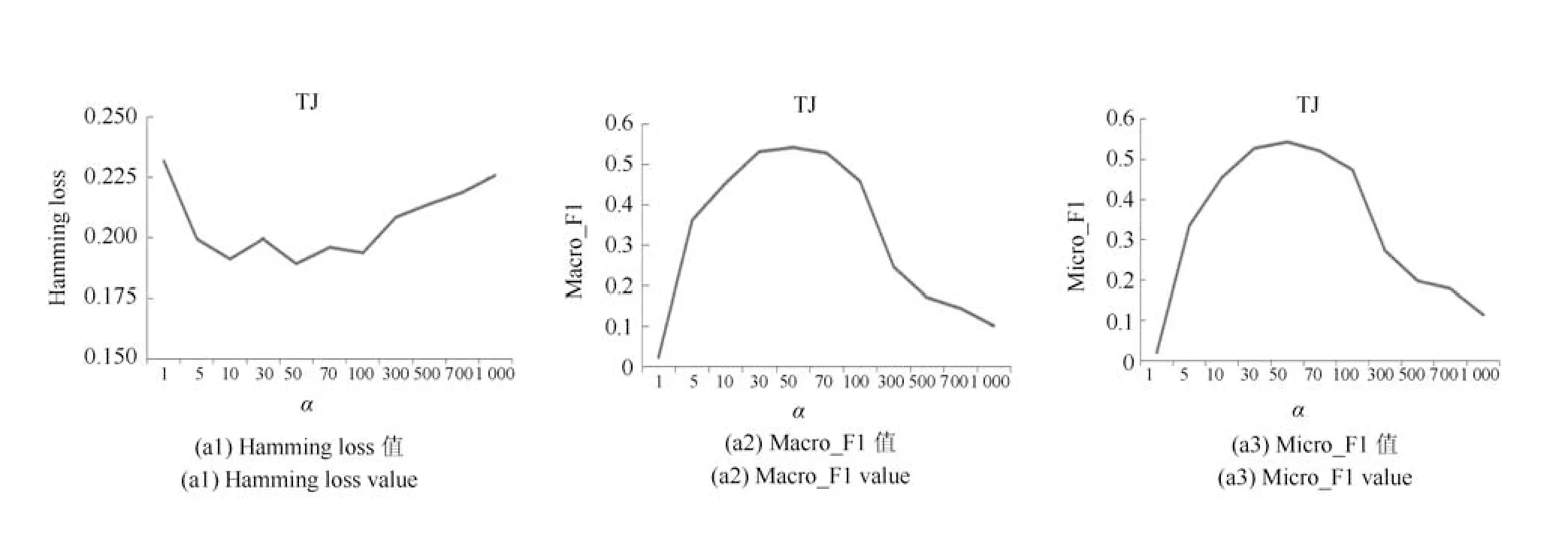
图3 α 的不同取值对数据集TJ 和enron 使用不同度量方式的性能体现Fig.3 The performance of Deep AE−MF on data sets TJ and Enronis with respect to different values of α and different metrics

图4 s/K 的不同取值对数据集EURLex-4K 和enron 使用不同度量方式的性能体现Fig.4 The performance of Deep AE−MF on data sets EURLex-4K and enron with respect to different values of s/K and different metrics

从图4 可以看出,对于hamming loss 在EURLex-4K 和enron 两个数据集上,随着s的增加,曲线总体先下降再升高(即性能先上升再下降);对于基于标签的Macro-F1 和MicroF1 在EURLex-4K 和enron 两个数据集上,随着s的增加,曲线总体先上升再下降(即性能先上升再下降).综合衡量图4 中的实验结果,EURLex-4K 和enron在s取值为0.6K附近时均达到最佳性能,因此选取s为0.6K作为最终的取值.

4 结论

本文提出基于SDAE 和矩阵分解的多标签分类算法Deep AE−MF 及Deep AE−MF+neg.Deep AE−MF 算法通过对SDAE 和MF 进行耦合得到一个特征嵌入和标签嵌入联合学习框架,能够有效地对特征非线性关系学习并同时用于标签嵌入学习中.Deep AE−MF+neg 算法在学习时利用标签之间的负相关(非共现)信息特点,提高标签嵌入学习以此最终提高模型的性能.实验结果表明,Deep AE−MF 及Deep AE−MF+neg 优于对比算法,能够有效地完成相关多标签分类任务.