一种基于最优状态点的无人车路径跟踪横向控制方法
2019-11-01王炳琪王春香
王炳琪 杨 明 王春香 王 冰
近年来,无人驾驶技术越来越成熟,路径跟踪横向控制作为无人驾驶的关键技术之一,吸引了众多国内外专家学者的关注.然而目前有关无人车路径跟踪的横向控制研究主要集中在高速公路或城区交通场景,而针对大中型车辆低速行驶在小区、施工导流路段等场景研究较少,这类场景空间狭窄、局部路径曲率较大(以下简称狭窄区域),大中型车辆很难安全裕度较大地通过.
目前国内外关于路径跟踪的研究可分为无车辆模型和有车辆模型这两类.预瞄PID 法[1−2]是常用的无车辆模型方法,这种方法最大优点是当预瞄距离足够大时,车辆稳定性可以保证,但当预瞄距离较大、路径曲率较大时,跟踪精度较低.有车辆模型的方法可以分为基于车辆动力学模型和基于车辆运动学模型这两类,车辆的横向动力学主要是在运动学基础上考虑了车辆运动时轮胎变形所产生的侧向力,Rajamani 认为车辆在低速行驶时,轮胎侧向力非常小,做出轮胎侧偏角为零的假设[3],即可忽略轮胎侧向力.文献[4]验证了当车辆前轮速度为9 m/s时,车辆运动学控制器和车辆动力学–运动学级联控制器在路径跟踪上的表现非常接近,因此可以认为车辆低速行驶时运动学模型足够适用.基于车辆运动学模型的方法主要有纯跟踪法[5−7]、基于前轮位置反馈(前轮控制)的方法[8−9]、基于后轮位置反馈(后轮控制)的方法[10−11]以及基于运动学的模型预测控制法[4,12].纯跟踪法在保证车辆稳定性的前提下控制精度较低,前轮控制和后轮控制各自只考虑了车辆前轮、后轮位置处的偏差,模型预测控制只考虑了重心以及重心处在预测时域内的偏差.这些方法只能保证车辆在某一位置具有很高的控制精度,而没有考虑车身整体的跟踪精度,因而难以保证整个车体安全裕度较大的通过狭窄区域.
针对这类情况,本文研究了整个车体的路径跟踪横向控制问题.其主要创新点包括:1)提出了车辆最优状态点和车辆最优参考状态的概念;2)为了求解车辆最优状态点,构造了车辆参考状态所对应的整体偏差这一目标函数;3)基于车辆运动学模型,依据最优状态点处车辆的横向偏差和航向偏差设计了横向反馈控制器.
1 问题描述
在狭窄区域中,车辆的可行路径十分有限,使得整个车体尽可能沿着参考路径这一条轨迹行驶,可以保证车辆安全裕度较大地通过狭窄区域,因此只考虑车辆特定位置处的跟踪精度是不够的.如图1所示,道路中间为路点拟合的参考路径曲线.考虑了车辆前轮位置和车辆后轮位置处偏差的方法,当狭窄区域路径曲率过大时,容易发生图1(a)和图1(b)中所示的碰撞.图1(c)考虑车辆与预瞄点处偏差,这样车辆会切弯而与拐角内侧发生碰撞.图1(d)则考虑了车辆重心处的偏差,这种情况车辆虽然可以通过狭窄区域,但安全裕度较小,碰撞风险较大,如图1(d)中圆圈标注处.
鉴于狭窄区域需要考虑到车辆的整体偏差,本文提出了车辆最优状态点这个概念,然后再根据该点与参考路径的偏差设计了反馈控制率,该方法提高了车辆低速行驶时的整体跟踪精度,可以有效提高车辆通过狭窄区域的安全裕度.
2 车辆最优状态点的选取
2.1 优化问题
为方便建立控制模型,将车辆简化为自行车模型,即分别将两个前轮、两个后轮合并为一个两轮模型,并且假设车辆平行于地面运动.该模型上前轮到后轮间的点定义为车辆状态点.参考路径上的点称为参考路径点.过车辆状态点沿垂直车体朝向作垂线,其与参考路径曲线的交点称为该车辆状态点对应的参考状态点.当车辆状态点与对应的参考状态点重合,且车辆航向角与对应的参考状态点处参考路径的航向角重合时,车辆的状态称为车辆参考状态,如图2 所示的车辆状态.图中ot为任意选取的车辆状态点的参考状态点,xtotyt为基于参考状态点建立的车辆坐标系,其横坐标轴代表车辆参考状态的朝向,纵坐标轴垂直于车辆参考状态的朝向.在车头到车尾的范围内,参考路径曲线沿垂直车体方向与车辆坐标系的xt轴围成的面积称为车辆整体偏差.

图1 狭窄区域车辆行驶示意图Fig.1 Vehicle driving illustration in a narrow area
显然,不同的车辆状态点对应了不同的车辆参考状态,不同的车辆参考状态所对应的整体偏差也不同,即车辆参考状态对应的整体偏差是一个与车辆状态点在车体所处位置有关的函数.因此寻找一个车辆状态点使得车辆参考状态所对应的整体偏差最小就可以表示为如下的优化问题,而该车辆状态点便称为车辆的最优状态点,该点对应的车辆参考状态称为最优参考状态.

其中ar为车辆状态点与车辆后轴中心的距离,即为该优化问题的可行解,gt(xt)为xtotyt坐标系下参考路径的曲线表达式,L为车辆前后轴距,f(ar)代表车辆参考状态对应的整体偏差,即为图2 中的灰色阴影部分的面积.
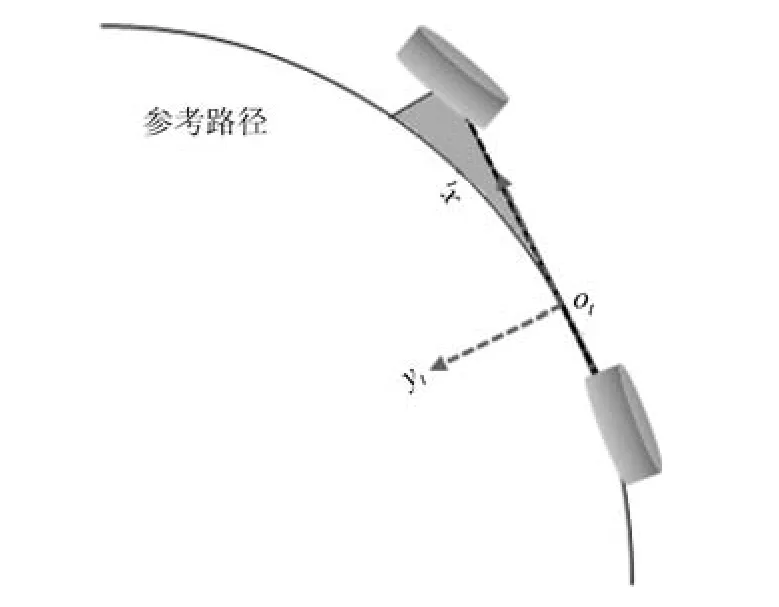
图2 车辆参考状态示意图Fig.2 The reference state of the vehicle
2.2 状态转移
为了求解上述优化问题,需要建立起xtotyt坐标系与车辆当前状态下的车辆坐标系之间的关系,如图3 所示.
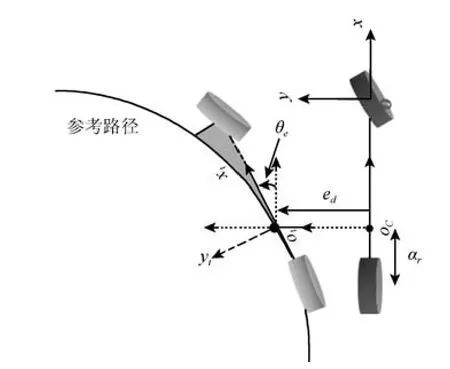
图3 车辆当前状态到参考状态的转移图Fig.3 The transfer from the current state to the reference state
车辆当前状态位于图3 右侧,由黑色表示,车辆参考状态位于图3 左侧,表示为灰色,xoy是基于车辆当前状态下前轴中心建立的坐标系,oc为车辆状态点的当前位置,g(x)为该坐标系下参考路径曲线表达式,ed为oc与参考路径的横向偏差[3],垂直于车体朝向,参考状态点在oc左侧时ed为正,θe为oc与参考路径的航向偏差,逆时针为正.显然
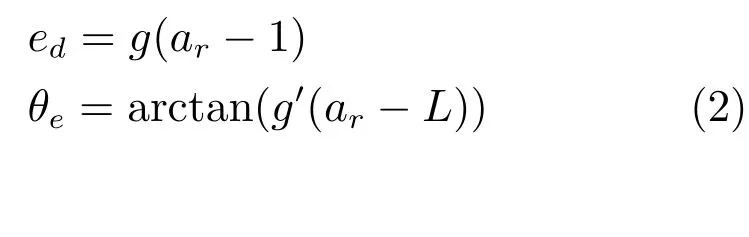
从图3 可以看出,xoy坐标系通过两次平移加一次旋转便可以转换到参考坐标系xtotyt.即
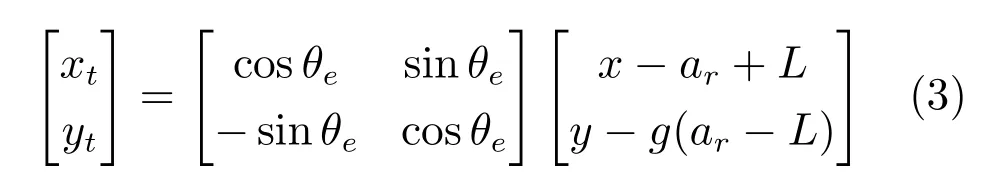
根据式(1)∼(3)可得目标函数在xoy坐标系下的表达形式
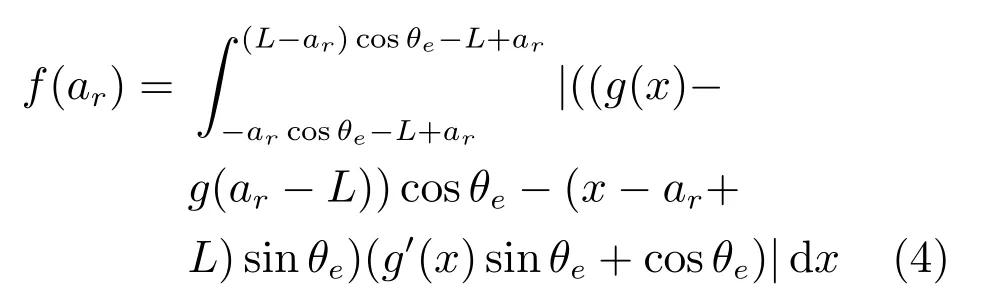
在狭窄区域中,可以认为车辆始终处于参考状态附近,为方便计算,在车辆参考状态点附近作如下近似
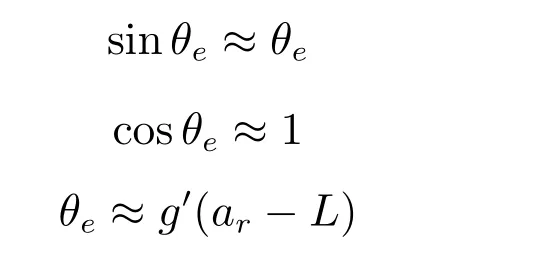
这样式(4)可简化为
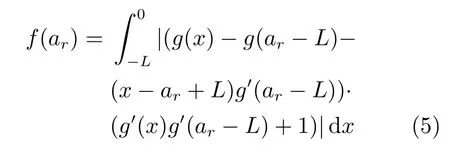
3 控制器设计
狭窄区域车辆行驶速度较低,根据文献[3−4]可知车辆运动学模型已足够适用.本文主要研究路径跟踪中的横向控制问题,假定车辆纵向速度恒定.
3.1 基于最优状态点的横向偏差模型
在车辆最优状态点处建立起的偏差模型如图4所示.其中Vf、Vr、Vc分别表示车辆前轮速度、后轮速度以及最优状态点处的速度,vx、vy分别为Vc沿车体方向和垂直于车体方向的分量,易得vx=Vr,本文认为车辆向前行驶,即vx为正,ICR为车辆瞬时转动中心,Rr为车辆后轮转弯半径.由图4 可知车辆在oc处横向偏差状态方程为
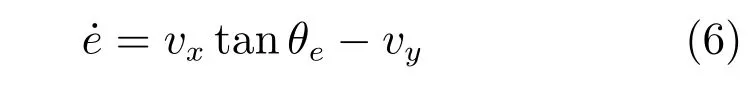
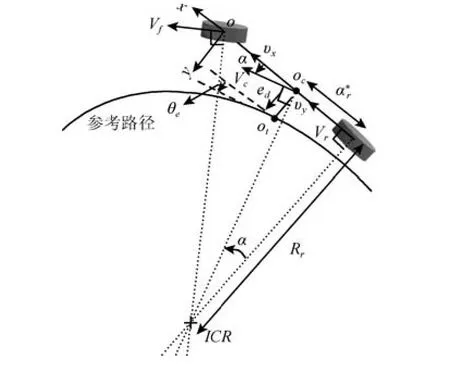
图4 车辆坐标系下的车辆运动学模型Fig.4 Kinematic model in vehicle coordinates
根据图4 中几何关系易得vy/vx=ar/Rr,将其代入式(6)则有如下结果:
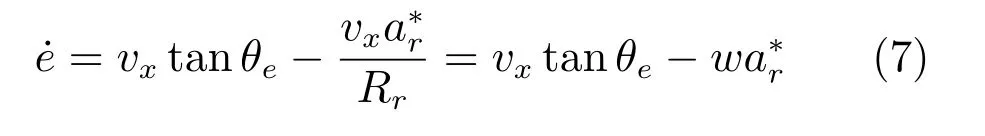
其中,w为车辆偏航角速度.
3.2 转向控制率设计
横向控制系统设计的目标是使得横向偏差ed和航向偏差θe收敛到零.由于车速较低,假定参考状态点在系统的一个采样周期内是不变的,这样参考点处的航向在一个采样周期是恒定的,则有=−w,本文参考文献[11]中的思想,设计了航向偏差反馈模型如下
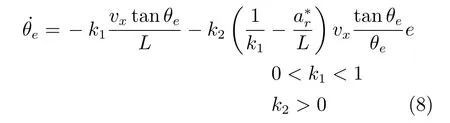
构造Lyapunov 函数
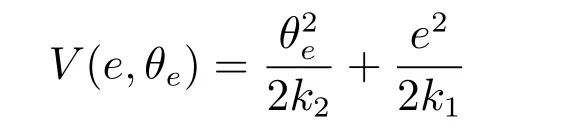
易知系统唯一的平衡点为(0,0),那么车辆沿任意轨迹(e(t),θe(t))运动时,V(e,θe)对时间的全导数为
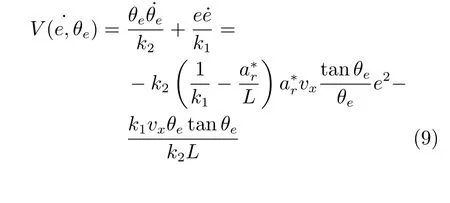
可以看出当不为0 时,(e,θe)是负定函数,当为0 时,˙V(e,θe)是半负定函数,且θe不恒为零,则该控制系统在平衡点处是渐近稳定的,所以θe和ed在平衡点附近收敛.根据=−w可得车辆转角控制律
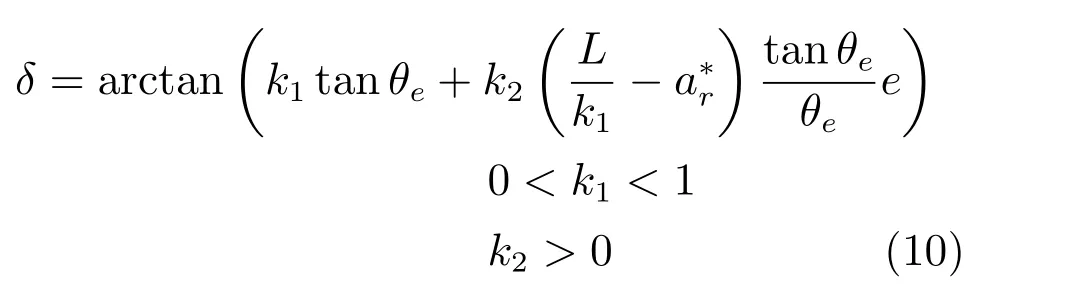
4 实验结果与分析
4.1 仿真平台
本文的仿真环境搭建在 MATLAB/SIMULINK 平台上,主要分为三个模块:参考曲线生成模块、路径跟踪模块以及车辆模型模块.
参考曲线生成模块主要是将采集到的GPS 路点在车前方一定范围内作曲线拟合,方便进行路径跟踪.路径跟踪模块是根据车辆位姿与参考路径的偏差生成控制量前轮转角.车辆模型模块是由车辆转向执行机构和车辆动力学模型组成,功能是通过输入前轮转角和车速得到车辆的当前位姿.
车辆转向执行机构近似由一阶惯性环节表示[13−14],车辆模型则是采用了2 自由度单轨车辆动力学模型[15].该模型是车辆动力学分析的基础,需要假定车辆没有纵向加速度并且是处于线性范围内的.由于本文研究的是车辆在狭窄区域的横向控制问题,因而已经假定过车辆纵向速度不变,Bundorf 于1967 年证明了当侧向加速度小于0.4 g时车辆可以认为是线性模型[16].本文实验采集了具有代表性的狭窄区域和城区道路数据,第一段狭窄道路数据中路径曲率半径最小为6 m,车速保持在10 km/h,所以最大的期望侧向加速度约为1.3 m/s2,第二段城区道路数据中路径曲率半径最小为14 m,车速保持在20 km/h,则最大的期望侧向加速度约为2.2 m/s2,都远小于0.4 g,因而该车辆模型适用于本文仿真,车辆参数如表1 所示.
4.2 仿真实验
本文实验场景选择具有代表性的单车道宽度狭窄区域和特定城区道路,其中狭窄区域是由交通锥桶模拟摆成.实验中参考路径由多项式曲线拟合生成,控制器参数为k1=0.85,k2=0.35.将本文方法与基于车辆运动学的模型预测控制、前轮控制、后轮控制、预瞄PID 以及纯跟踪这几种方法作对比,并绘制前后轮轨迹图.如图5 和图6 所示,实线代表后轮轨迹,虚线代表前轮轨迹.为统一量纲,采用车体平均偏差代替车辆当前状态所对应的整体偏差eall,其中=eall/L,并且统计了车辆当前状态从前轮到后轮的最大偏差.
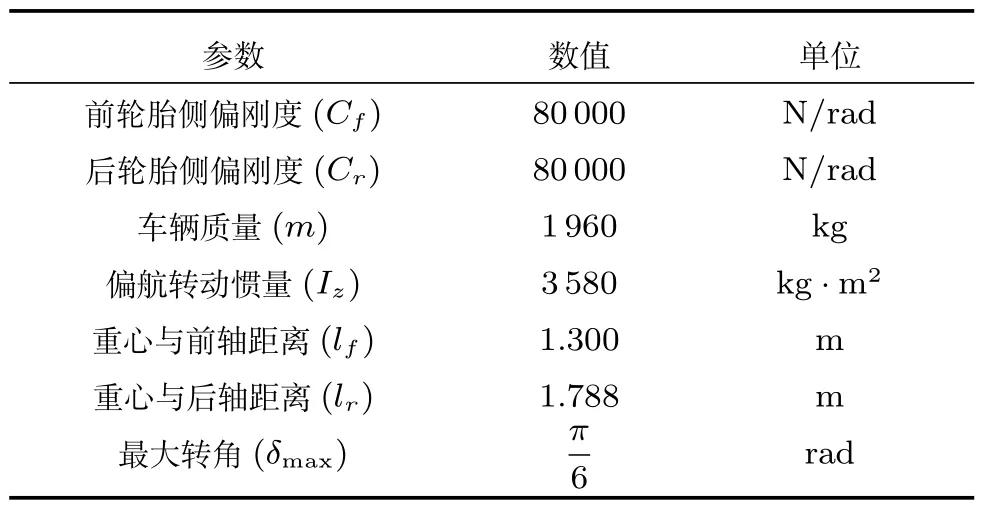
表1 车辆参数Table 1 Vehicle parameters
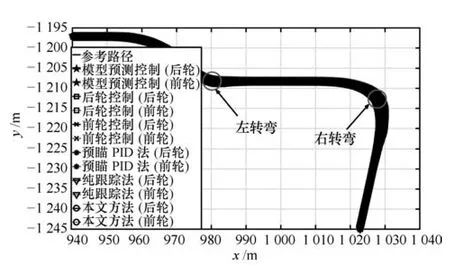
图5 狭窄区域车辆前后轮行驶轨迹图Fig.5 The front wheel and rear wheel path in a narrow area

图6 城区场景车辆前后轮行驶轨迹图Fig.6 The front wheel and rear wheel path on the urban road
4.2.1 狭窄区域场景
车辆在狭窄区域行驶轨迹如图5 所示,从左上角行驶至右下角,车速为10 km/h.方便观察,取最小曲率半径约为11 m 左转弯和最小曲率半径约为6 m 的右转弯处轨迹放大并绘制相应场景中的偏差曲线,如图7 和图8 所示.表2 和表3 显示本文方法对应的车体平均偏差和最大偏差均好于其他方法,并且在车体最大偏差这一指标上的优势更加明显,这在狭窄区域中更为重要,因为其可以直接反映车辆通过的安全裕度.
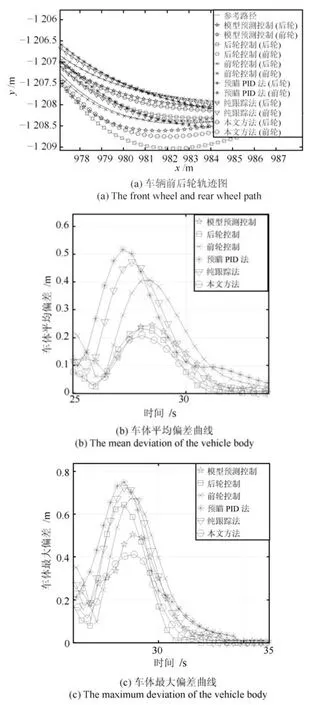
图7 左转弯道场景Fig.7 The left corner
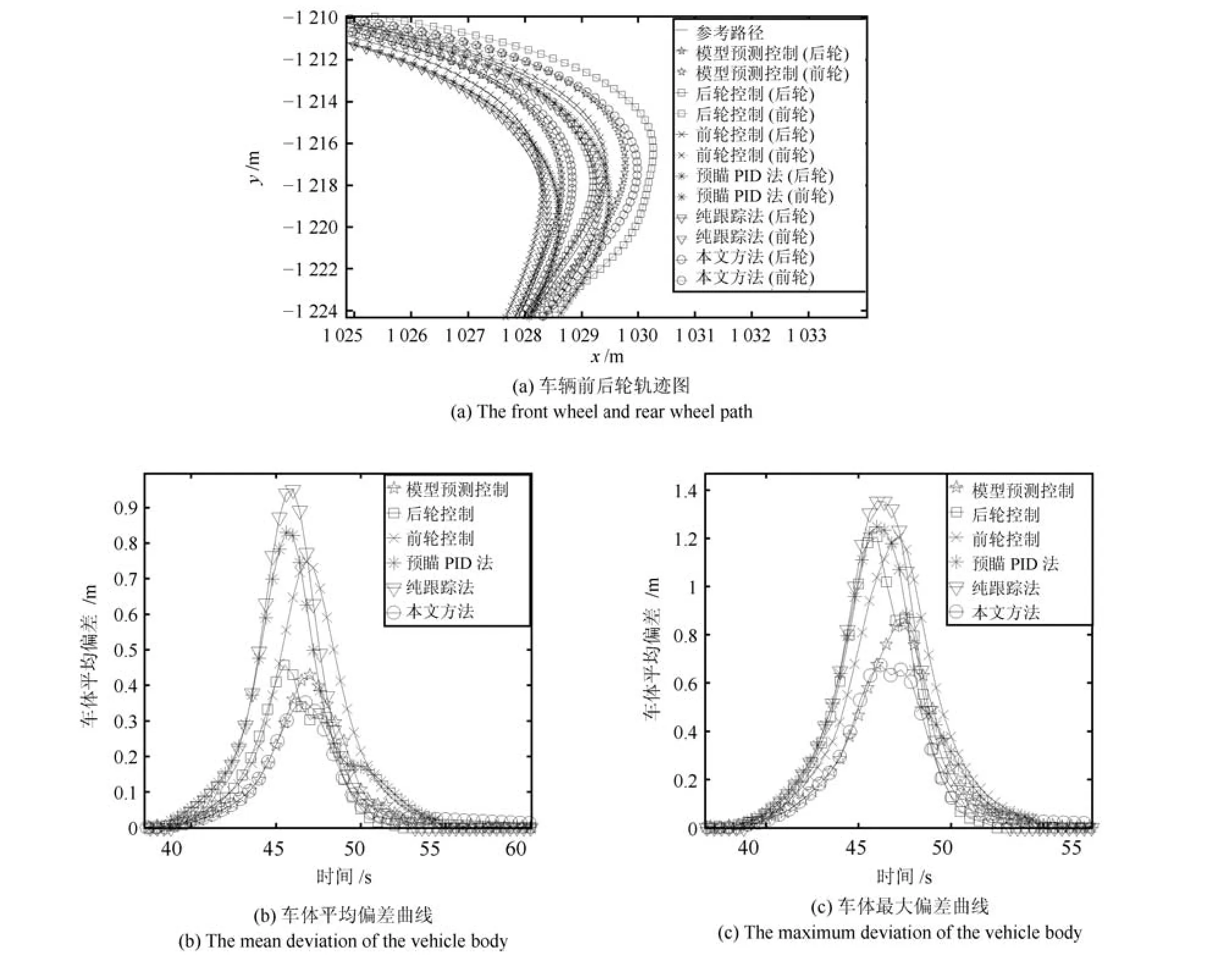
图8 右转弯场景Fig.8 The right corner
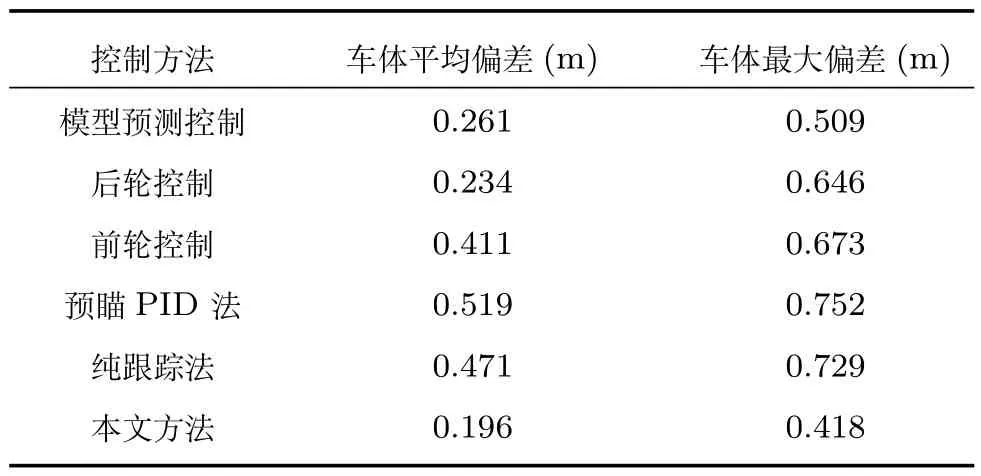
表2 左转弯场景偏差对比Table 2 A comparison of the deviation on the left corner
由图7(a)和图8(a)可以看出,本文方法对应的车辆前后轮轨迹相对最贴合参考路径,预瞄PID法和纯跟踪法在保证车辆稳定性的前提下发生了较大程度的切弯,因而跟踪精度较低.前轮控制和后轮控制在车辆特定位置处跟踪精度较高,整体跟踪精度较低,但由于后轮控制考虑了每个采样时刻内参考路径相对车辆的航向变化,所以车体平均偏差好于前轮控制,如图7(b)、图8(b)所示.模型预测控制在预测时域范围内车辆重心的跟踪精度较高,因其只考虑了预测范围内的偏差,但并没有将其扩展到车辆整体,所以整体跟踪能力依然不如本文方法.
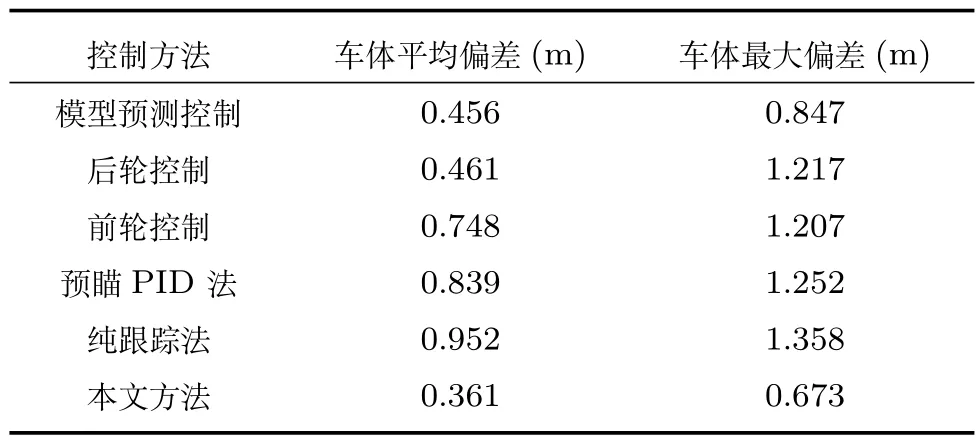
表3 右转弯场景偏差对比Table 3 A comparison of the deviation on the right corner
4.2.2 城区道路场景
城区道路场景由一段小曲率弯道、最小曲率半径为14 m 直角弯道和最小曲率半径为25 m 的“S”型弯道组成.车辆行驶轨迹如图6 所示,车速恒定为20 km/h,车辆由右上角行驶至左下角.
将图6 中圆圈标注的3 个场景车辆轨迹图放大并绘制相应场景中的偏差曲线,如图9∼11 所示.统计这些场景中对应的车体平均偏差和车体最大偏差,如表4∼6 所示.
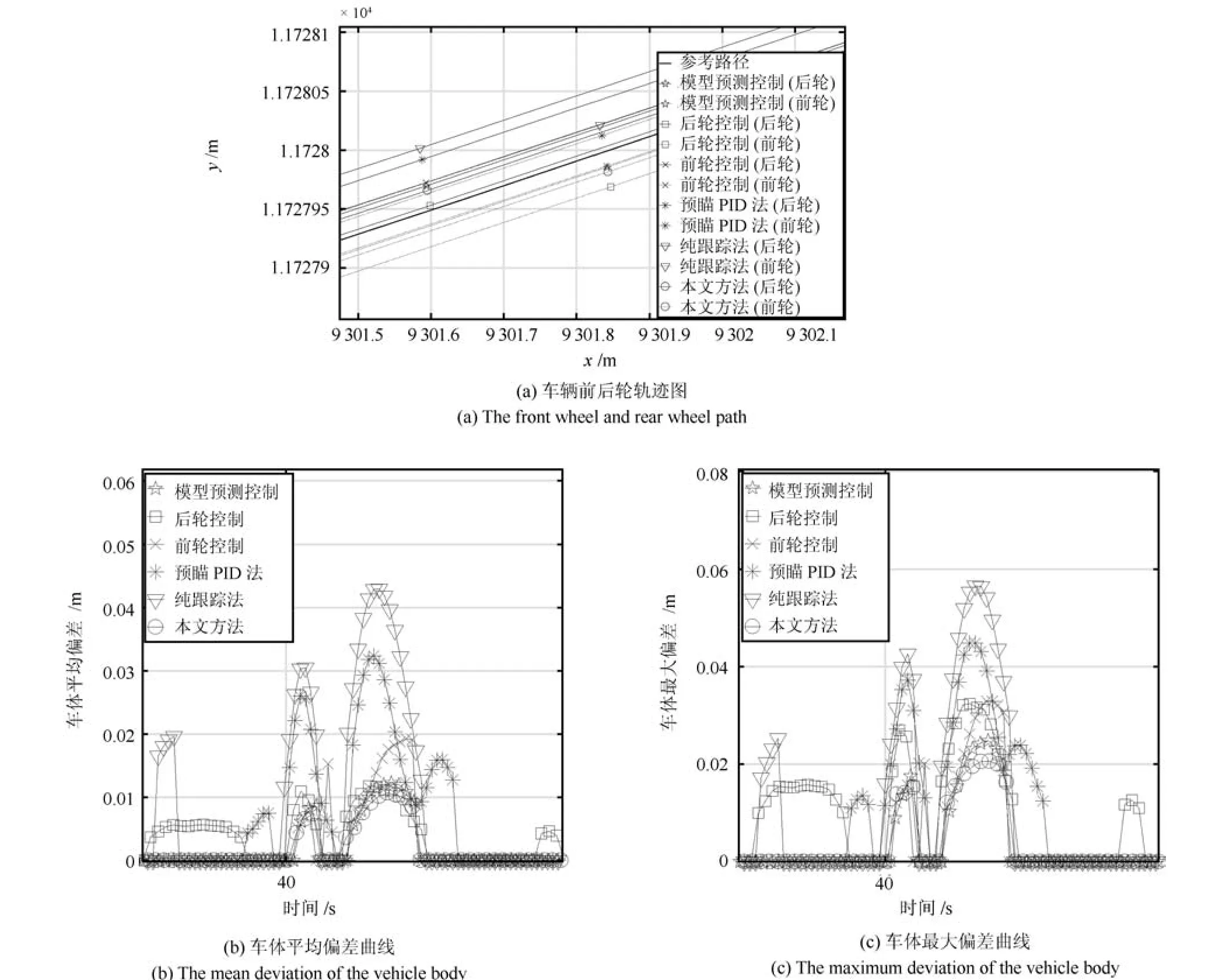
图9 小曲率弯道场景Fig.9 The small curvature road

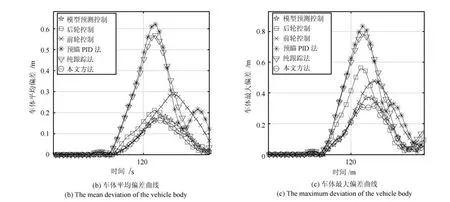
图10 直角弯道场景Fig.10 The right angle road
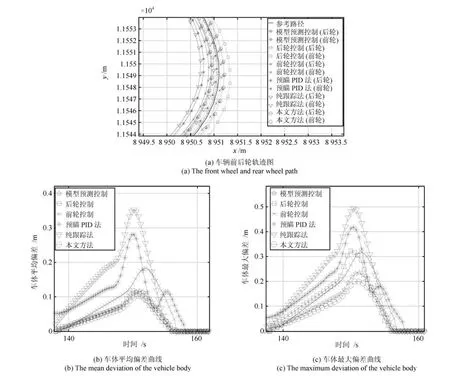
图11 “S”型弯道场景Fig.11 The“S”curved road
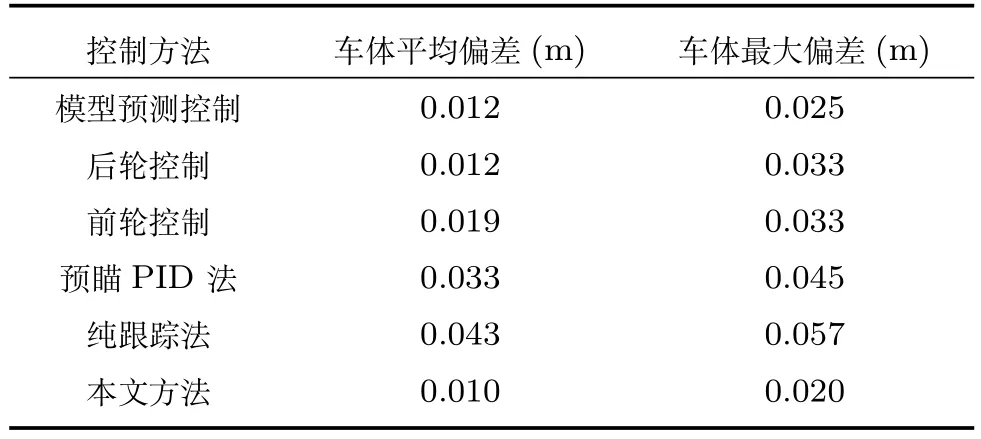
表4 小曲率弯道场景偏差对比Table 4 A comparison of the deviation on the small curvature road
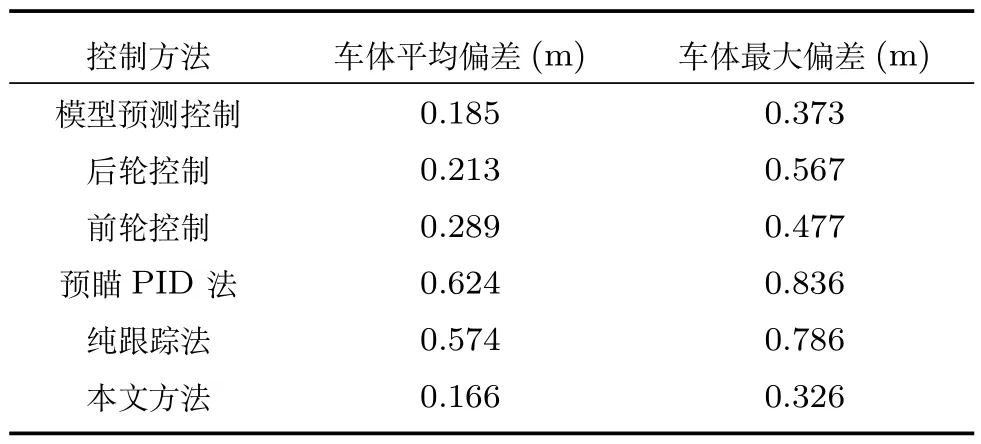
表5 直角弯道场景偏差对比Table 5 A comparison of the deviation on the right angle road

表6 “S”型弯道场景偏差对比Table 6 A comparison of the deviation on the“S”curved road
据表4∼6 可以看出,不论是在小曲率弯道、直角弯道还是“S”型弯道,本文方法对应的车体平均偏差和车体最大偏差均小于其他方法.从图9(b)∼(c)和图11(b)∼(c)中可以看出,本文方法相对预瞄PID 法、纯跟踪法、前轮控制以及后轮控制在整体跟踪精度方面优势比较明显,但相对模型预测控制优势较小,是因为这两种场景中的路径曲率变化比较平缓,所以本文所选取的最优状态点会处于车体中心附近,这与模型预测控制所考虑的偏差位置是接近的,而随着曲率变化增大,车辆的最优参考状态变化增大,其对应的最优状态点位置变化也会增大,本文方法的优势会逐渐增大,如图10 和表5 所示.因此,本文方法不仅在狭窄区域车辆整体跟踪精度较高,在城区场景相对其他方法的表现也更好.
5 结论
针对大中型车辆难以安全裕度较大地通过狭窄区域这一问题,本文提出了一种基于车辆最优状态点的横向控制方法.首先通过构造车辆参考状态对应的整体偏差这一目标函数.求解出了车辆最优状态点,并给出了对应的车辆最优参考状态,即提供给车辆可以提高整体跟踪精度的最优目标.接着基于该最优状态点处的偏差,建立了车辆横向控制模型.对比实验结果表明,不论在狭窄区域还是在城区道路场景中,本文方法都有效地提升了车辆低速行驶时的整体跟踪精度,可以保证车辆安全裕度较大地通过狭窄区域.另外,把车辆纵向速度纳入这类问题考虑范畴将是未来进一步开展的工作.
