瞻前顾后，为整数乘法画句号——《三位数乘两位数》教学设计

张 慧

【教学内容】

人教版四年级上册第47 页。

【教学过程】

一、前概念再现

师：同学们，我们学过三位数乘一位数和两位数乘两位数，你们会笔算145×2 和45×12 吗？

学生独立计算，集体订正，回忆两位数乘两位数的计算方法。

【设计意图：调动学生已有知识经验，为自主建构新知识做铺垫的同时，为培养迁移能力和感受乘法知识连贯性埋下伏笔。】

二、自主迁移，建构新知

师：三位数乘一位数和两位数乘两位数你们已经会算了，我们今天一起来研究《三位数乘两位数》。

1.审题并列式。

出示例题：李叔叔从某城市乘火车去北京用了12 小时，火车每小时行145 千米。该城市到北京有多少千米？

学生审题并列式：145×12。

2.借助估算，判断乘积所在区间。

师：有四位同学已经尝试笔算145×12，你能不能一眼看出他们当中谁算错了？

课件出示：①145×12=740

②145×12=1600

③145×12=1740

④145×12=3040

生：①错了，最小的三位数和12 相乘都超过了1000。

生：④错了，把145 看成150，12 看成20，得数才是3000。

【设计意图：估算一直是学生学习的一个难点，因此，本设计灵活处理教材，将直接估算145×12的取值范围改为判断别人的计算结果是否正确的方式呈现，虽然降低了难度，但学生仍然获得了估算的机会。】

3.自主探究计算。

师：②、③哪个错了？请同学们笔算一下，看看到底等于多少。

学生独立计算，一人板演。

全班汇报计算过程。

【设计意图：用估算的办法不容易判断②和③究竟谁对谁错，想解决这个问题还得借助于笔算，而笔算的方法与学生原有的两位数乘两位数算法是相同的，因此可以放手让学生利用前概念独立计算出得数。】

4.概括并验证算法。

师：同学们会计算这个三位数乘两位数的题目了，那如果有人问你三位数乘两位数怎样算，你怎样讲给他听呢？

四人小组概括算法。

生：末位对齐；从个位乘起；两位数的个位与三位数乘，积的末位与个位对齐；十位上的数与三位数乘，积的末位与十位对齐。

师：计算两位数乘两位数时，个位上的数与第一个因数乘，积的末位与个位对齐；三位数乘两位数时，个位上的数与三位数乘，积的末位就一定与个位对齐吗？

生：个位上2×145 等于290，是290 个“一”。

师：十位上的乘积呢？

生：1450，也就是有145 个十。

师：我们总结出了三位数乘两位数的计算方法，一起来读一读。

【设计意图：三位数乘两位数可以让学生自主迁移两位数乘两位数的算法来总结新算法，而后经历质疑与验证，将两位数乘两位数的算理再加工，从而理解三位数乘两位数的算理，并验证对于三位数乘两位数与两位数乘两位数算法相同的猜想。】

5.多位数乘三位数。

师：如果百位上的数与三位数乘，积的末位应该与哪一位对齐，表示什么？

生：表示有几个百，与百位对齐。

师：千位上的数乘呢？

生：与千位对齐，表示有几个千。

【设计意图：三位数乘两位数是整数乘法的结束课，学生在本节课中不仅要建构三位数乘两位数的计算方法，同时又要向多位数乘多位数的计算迁移。在本环节中，学生借助计数单位来解释乘法的意义，在思考某一位上的数与三位数乘的意义中感受到了知识是可延伸的。】

6.两位数十位上的数与三位数百位上的数相乘。

师：同学们已经掌握了三位数乘两位数的方法，刚才老师请同学们判断了四位同学的做法，其中第一位同学错在哪里呢？

生：漏掉了十位上的“1”与百位上的“1”相乘所得的“1”。

7.小结——延伸。

师：1740，这个计算结果对吗？我们用计算器检查一下吧。

师：三位数乘两位数与两位数乘两位数一样，不管个位上的2 与45 相乘还是与145 相乘，积的末位我们都是与个位对齐，表示多少个一；十位上的数去乘，积的末位都与十位对齐，表示多少个十。原来三位数乘两位数的算法和两位数乘两位数的算法是一样的。如果再有两位数乘四位数，怎样算呢？

生：算法与三位数乘两位数一样。

【设计意图：教学不能止步于知识的传授，还要将数学知识进行适当的拓展和延伸。】

三、巩固提升

1.竖式计算，建立模型。

师：看来同学们学会了三位数乘两位数的算法，请你在练习纸上试着计算下面两题吧。

独立计算后，投影个别学生的练习并集体说理。

师：假如不给你具体的数字，你能说说各部分表示什么吗？

师：第一个框表示什么呢？

生：表示多少个“一”。

师：下面的方框表示什么呢？

生：表示有多少个“十”，与十位对齐。

【设计意图：通过直观图的形式帮助学生建立笔算乘法的模型。学生借助模型，从宏观上再次理解笔算乘法的意义，使得乘法的意义在学生心中一般化。】

2.54×145。

师：再来试试这一题吧，想一想用什么方法好呢？

学生独立计算后，展示两种不同计算方法。

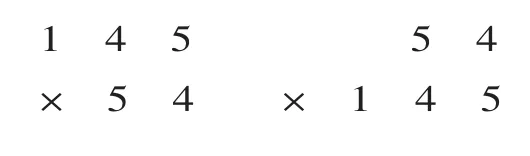
师：这两位同学的计算方法不同，计算结果都正确。你觉得两种计算方法哪种好？

生：第一种好，把145 放上面只有两行算式，54 放上面有三行算式，容易错。

师：虽然把54 放上面容易出错，老师还是想问问第三行的54表示什么呢？

生：54 个“百”。

师：经验告诉我们把数位多的数写在上面不容易出错。

【设计意图：本题两种解法都对，但学生要会选择最优的方法，因此提倡学生交换两个因数的位置，用145×54。学生通过互相启发，发现“两乘加”要比“三乘加”计算起来更容易。】

3.渗透数学文化。

师：同学们，这是古代欧洲计算三位数乘两位数的方法，你能看懂吗？

学生解释计算过程。

师：这几个“6”是什么意思呢？

生1：第一个6 是个位的3与十位的2 相乘得到的，表示6个“十”。

生2：第二个6 表示6“百”。生3：第三个6 表示6 个“十”。师：有人说，笔算三位数乘两位数就是算算有几个“一”、几个“十”、几个“百”，最后把几个“一”、几个“十”、几个“百”加起来，有道理吗？

【设计意图：渗透了数学文化的同时又逐步分析了笔算乘法意义，拓展学生的视野。学生在这道题目中感受到了计算方法多样性和文化的多样性。】

四、总结延伸

师：同学们猜，如果以后再学习乘法，会学习什么内容呢？

生1：四位数乘三位数。生2：五位数乘四位数。

师：猜错了，以后都不学多位数的笔算乘法了，知道为什么吗？

生：和三位数乘两位数的计算方法一样。

师：我们学了三位数乘两位数，以后遇到多位数乘多位数的时候可以用三位数乘两位数的方法来计算。