沟渠·线段图·数感——以图为媒，培养学生数感

石 荣

冬日的田野一片寂寥，偶有紫色的草籽点缀其中，一条用以灌溉的沟渠穿越而来，直至中部的河堰。儿时和小伙伴们在这里嬉戏打闹，经过沟渠之时，他们都能一跃而过，个小的我却只能寻个稍窄的地方慢慢探身跨过去。那时的我不明白，小伙伴们怎能毫不犹豫地就跳过去了，而我会知道自己跳不过去，好像有一股神秘的力量在操纵着这件事。现在想来，这股神秘的力量应该就是潜伏在人身上的一种数学素养——数感。数感平时是看不见摸不着的，而在主人需要的时候它就会及时出现。如果沟渠的宽度用线段一来表示，双腿跨过的距离用线段二来表示，那么只要线段一的长度不超过线段二的长度，就能安全跨过沟渠。二者的长短不需要拿尺子测量，孩子们自身就有这个能力估计两者之间的长短关系。这使我想起三年级上学期（人教版三上）在教学归总问题时课堂上画线段图的情景。

例题：妈妈的钱买6 元一个的碗，正好可以买6个。用这些钱买9 元一个的碗，可以买几个？

读题后，为了让学生更透彻地理解题意，我让他们在作业本上画线段图。在巡视的过程中，我发现对于“6 元一个的碗正好可以买6 个”这个条件，学生都能正确地用线段图表示出来，而怎么表示“9 元一个的碗”却是有些图不达意。因而在示范画图时，画好6 个6 元一个的碗后，我问学生：9 元大概要画多长呢？大多数学生是很茫然的，其中一名学生却是高高地举起了手，他说：先画和6 元的线段一样长的线段，9 元比6 元多3 元，3 元是6 元的一半，所以还要再多画6 元的一半。他的表述清楚，我欣喜地发现这个学生的数感是强烈的，而且他能借助所学过的数学知识来表述他所理解的数学信息。同时，我意识到线段图形象直观，是培养学生数感的一个很好的媒介。于是，在教学中我以线段图为切入口，有意识地让学生更多地画线段图，以达到提高学生数感的目的（以人教版三上数学教材为例）。

一、利用线段图理解概念，在概念教学中培养数感

数学概念不仅是数学基础知识的重要组成部分，而且是学习其他数学知识的基础。学生掌握基础知识的过程，实际上就是掌握概念并运用概念进行判断、推理的过程。数学中的法则都是建立在一系列概念的基础上的。事实证明，如果学生有了正确、清晰、完整的数学概念，就有助于掌握基础知识，提高解题技能。因而数感的培养应渗透于概念教学。“倍”是三上教材中一个很重要的概念，与乘法、除法、分数、比等概念在本质上有着内在的联系，在教材的编排体系中起着承前启后的作用。在教学《倍的认识》这一课时，设计了以下环节：

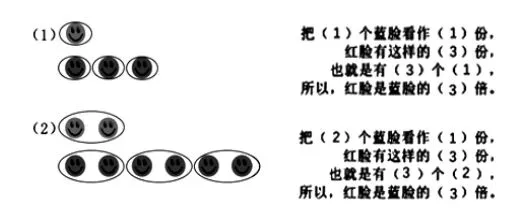
图1

图2

图3

图4

图1 是实物图，在初步接触倍的概念后，教师贴一个蓝脸，学生贴出它的三倍；教师贴两个蓝脸，学生还是贴出它们的三倍。学生在这个练习中进一步理解倍的意义，同时初步体会“比较量数量增加，比较量中的每一份都增加相同的数量，那么比较量和标准量之间的倍数关系是不变的”。在此基础上，实物图变化为图2 的椭圆形图，接着抽象成图3，进而变化成更为抽象的图4——线段图。在这个过程中学生体会“图形变而倍数关系不变”，思维经历由形象到抽象的变化。利用线段图进行比较量和标准量的计算，在用数字计算的基础上用字母来表示：如果标准量用x 来表示，那么比较量就用3x 表示，渗透符号思想。在多次的数量计算中感受数的变化，比较数的大小，感悟数量之间的倍比关系，以达到培养数感的目的。

二、利用线段图比较大小，在比较中增强数感

在具体的情境中把握数的相对大小关系，不仅是理解数的需要，同时也会加深学生对数的实际意义的理解，使数感得到发展。分数是人教版三年级上册教材的又一重要数学概念，与学生已有的整数概念是完全不同的。不足一个的物体的数量怎么表示在学生的经验中是缺失的，特别是对这些数的大小的概念更是模糊不清，学生很容易根据以往的经验判定小于。教师在教学分数的大小比较时，往往会借助各种图形来辅助。而笔者最喜欢用线段图，因为线段图能清楚地表示数量的大小、表达数量之间的关系，是解决数学问题最重要的辅助手段之一，并且线段图简单易画，可以节省时间，提高效率。

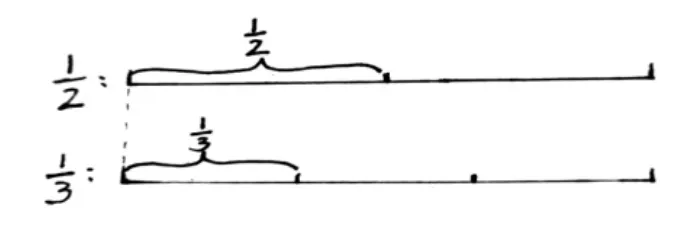
图5

两条同样长的线段（单位“1”），一条平均分成2份，一条平均分成3 份，其中的1 份哪个长？当然是平均分的份数越少，1 份就越长，如图5。用线段图表示，它们的大小关系会一目了然。

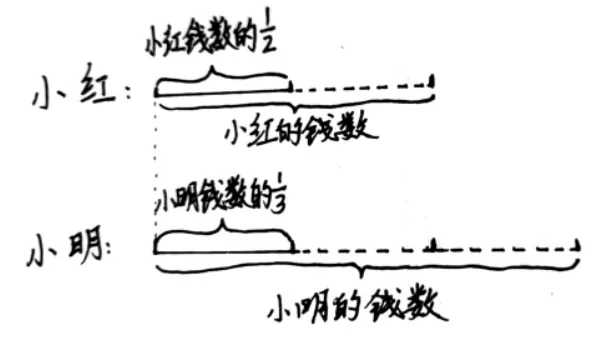
图6

这道题对于刚刚接触分数的三年级的学生来说，理解起来是有一定难度的。那么线段图在这里绝对有四两拨千斤的作用。笔者先引导学生画出一条线段表示小红钱数的，接着画出同样长的线段表示小明钱数的（因为同一本书的价钱是同样多的）。再通过理解和的意义补充画出小红的总钱数和小明的总钱数，如图6，谁的钱多一看一比就出来了。

在教学中要求学生多画线段图，养成画图的良好的解题习惯，借助线段图通过观察比较增强学生对数、数量的敏感度，培养对数的感觉，丰富对数的感悟，以达到培养学生数感的目的。

三、利用线段图厘清数量关系，在清晰数量关系中提升数感

线段图能使复杂问题简单化、抽象问题具体化，是优化解题过程的重要途径之一。用线段图把问题中的各个数量及其相互关系表示出来，数形结合使问题的内容具体化、形象化，能帮助学生理解题意，搞清数量之间的关系，寻找出解题的方法。

如，小猴和妈妈上山摘桃，小猴摘了4 个，妈妈拿一个桃子给小猴后，刚好是小猴的3 倍，猴妈妈一共摘了多少个桃？

刚刚学习了倍的知识的学生，对于题中的数量关系一时是弄不清楚的。于是我指导学生画了下面的线段图：

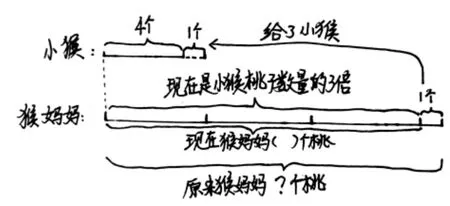
图7

在反复读题理解题意的基础上一步一步引导学生画图，搞清楚每一个信息用图怎么表示，特别是“3倍”的含义：谁是谁的3 倍，标准量是什么。通过图让学生理解了猴妈妈拿了一个桃给小猴，桃的数量减少了一个，而小猴增加了一个桃，桃的数量变成了5个，“3 倍”指的是“猴妈妈拿走了一个桃后桃子的数量是小猴增加了一个桃后桃子的数量的3 倍，也就是5 个桃的3 倍，标准量是5 个桃。厘清了这个数量关系，此题就迎刃而解了。

小学生的思维特点是以具体形象为主，通过长期的训练让学生养成画图的习惯，有利于学生的思维从形象思维向抽象思维过渡。要让学生在常态的长期的画图训练中经历运用符号和图示描述现实问题的过程，以此建立符号感，发展抽象思维，以达到提升数感的目的。

总之，以线段图为媒，数形结合，以形助数，是学习数学的重要方法，是解决问题的重要策略，也是培养和提升学生数感的强有力的手段。