任意阶梯型截面Timoshenko 梁的弯曲

杨 骁,钱 程,钱雪薇

(上海大学土木工程系,上海200444)

在梁弯曲变形的研究中,通常将其边界约束视为简支或固支等理想边界条件.虽然这种处理方式具有一定的合理性,并可简化计算分析,但对于梁边界的某些特殊连接形式,如木结构的榫卯连接、PC(prestressed concrete)结构中的结点等,应用理想边界条件分析梁弯曲可能会产生较大的误差；另外,阶梯型截面梁构件已广泛应用于机械和建筑结构等工程领域中,因此边界弹性支承下阶梯型截面梁的弯曲研究及其应用具有重要的理论意义和广泛的应用背景.

阶梯型截面梁弯曲分析的经典解析方法是以截面变化位置为分界点,将梁分为若干等截面子梁段,并对每一子梁段应用等截面梁弯曲的控制方程求其变形通解,而后根据梁的边界条件以及子梁段连接处的连续性条件,确定子梁段变形通解中的待定常数[1],或利用传递矩阵法进行求解[2-5],从而得到以分段函数形式表示的阶梯型截面梁的弯曲解.然而,随着梁变截面个数的增加,其连续性条件或传递矩阵数目增加,导致确定待定常数的线性方程组阶数增加或矩阵计算量增大,求解繁琐,难以给出形式简单的解析闭合解.为此,众多学者试图寻找适用于整个梁跨的形式简单的解析闭合解.

阶梯型截面梁弯曲分析的另一种方法是基于广义函数理论中Heaviside函数性质[6],在整个梁跨上给出包含不连续信息的微分控制方程,从而减少计算,简化分析.Falsone[7]给出了包含载荷、挠度、转角以及曲率不连续等信息的Euler-Bernoulli梁弯曲控制方程；而Yavari等[8-10]针对Euler-Bernoulli梁挠度、转角和曲率的不连续跳跃,通过构造一个事先满足跳跃条件的新挠度函数,在整个梁跨上给出了梁弯曲的控制方程,并提出了辅助梁分析方法；Biondi等[11]针对单阶梯型截面梁或梁中存在一个内部扭转弹簧的梁弯曲问题,在梁抗弯刚度中分别引入广义Heaviside函数和Dirac's Delta函数,给出了Euler-Bernoulli梁弯曲的控制方程以及适用于整个梁跨的解析闭合解；Biondi等[12]还将文献[11]的结果推广至多阶梯型截面梁以及内部多扭转弹簧梁的弯曲分析中,并研究了梁柱轴向位移的不连续性问题,但其抗弯刚度的物理描述并不十分完善；Cheng等[13]利用广义函数给出了阶梯型截面梁的静动力分析方法,并利用得到的解析闭合解进行了相关的参数敏感性问题分析.同时,广义函数亦应用于非均匀梁弯曲分析及无损检测等方面[14-21].

目前,在阶梯型截面Timoshenko梁弯曲研究中广义函数的应用相对较少,本工作应用Heaviside函数研究了边界弹性支承阶梯型截面Timoshenko梁的弯曲.首先,利用Heaviside函数,给出了任意阶梯型截面Timoshenko梁的抗弯和抗剪刚度,进而得到了任意载荷作用下阶梯型截面Timoshenko梁弯曲的解析通解；然后,利用边界弹性支承条件,确定通解中的待定常数,从而得到阶梯型截面Timoshenko梁弯曲变形的解析闭合解；最后,并利用SAP2000有限元软件验证了解析闭合解的正确性.在此基础上,本工作还数值分析了固支和悬臂阶梯型截面Timoshenko梁的弯曲,考察了变截面位置、截面大小、梁高跨比以及边界支承刚度等对Timoshenko梁弯曲变形的影响.

1 任意阶梯型截面Timoshenko梁的弯曲变形

如图1所示,设承受横向载荷q(x)作用的阶梯型截面Timoshenko梁由N段矩形等截面子梁构成,其总长为L,且在x=xi(i=1,2,···,N-1)处发生截面变化.记第i段子梁横截面的高和宽分别为hi和bi,而其抗弯刚度和抗剪刚度分别为(EI)i和(GA)i；假定梁两端为弹性支承,其竖向弹簧刚度分别为Kd1和Kd2,而横截面扭转弹簧刚度分别为Kr1和Kr2.

利用Heaviside函数[6]以及文献[11]的方法,可得到此阶梯型截面Timoshenko梁沿梁跨的抗弯刚度(EI)(x)和抗剪刚度(GA)(x)分别表示为

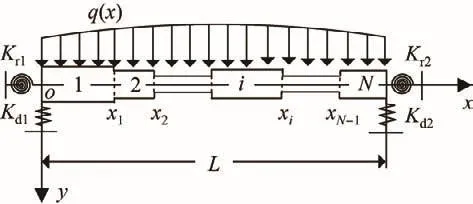
图1 阶梯型截面Timoshenko梁Fig.1 Timoshenko beam with stepped cross-section

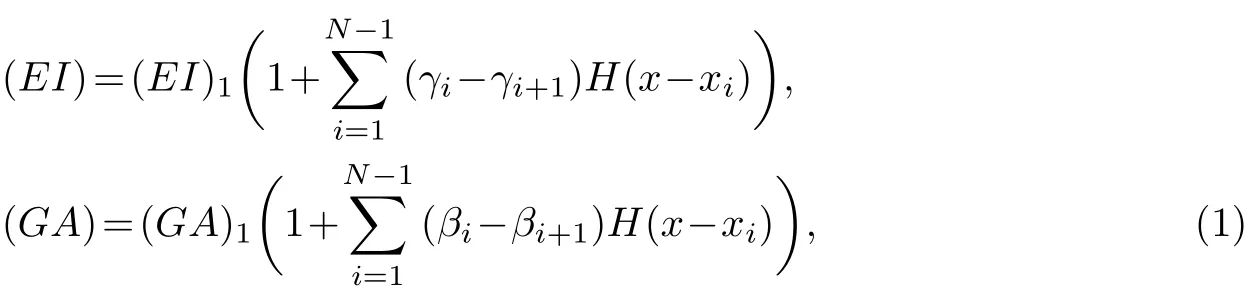
式中,H(x)为Heaviside函数,γi和βi分别为抗弯刚度和抗剪刚度的折减参数,定义为

如果记阶梯型截面Timoshenko梁的横向挠度和截面转角分别为w(x)和φ(x),则任意载荷q(x)作用下阶梯型截面Timoshenko梁弯曲变形的边值问题[1]为

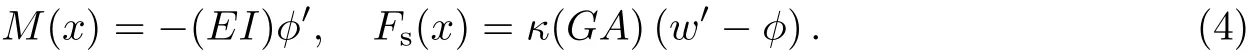
引入如下无量纲量和参数

可得如下阶梯型截面Timoshenko梁弯曲的无量纲边值问题

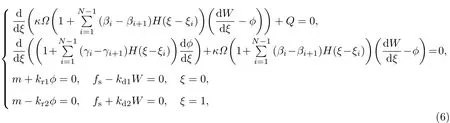
式中,m=ML/(EI)1和fs=FsL2/(EI)1分别为Timoshenko梁的无量纲弯矩和剪力,且

对方程式(6)的第一个方程两边积分,可得

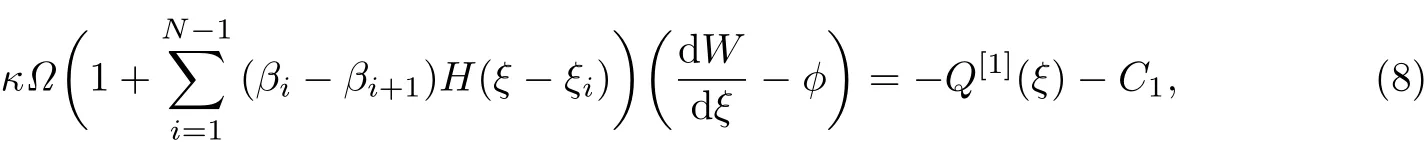
式中,C1为待定系数,且

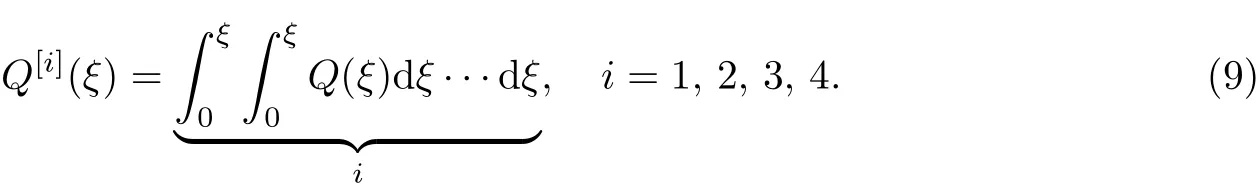
将式(8)代入式(6)的第2个方程,两边积分得

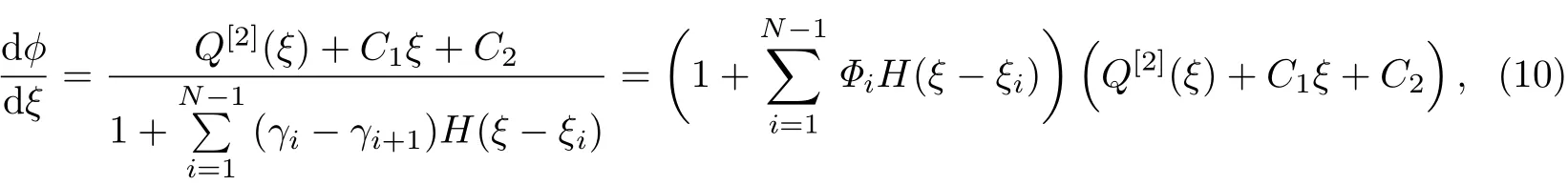
式中,C2为待定系数,且

于是,有

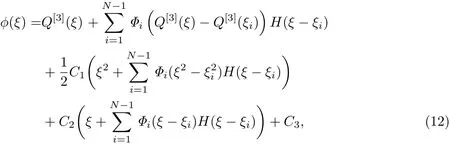
式中,C3为待定系数.

将式(12)代入式(8),两边积分得

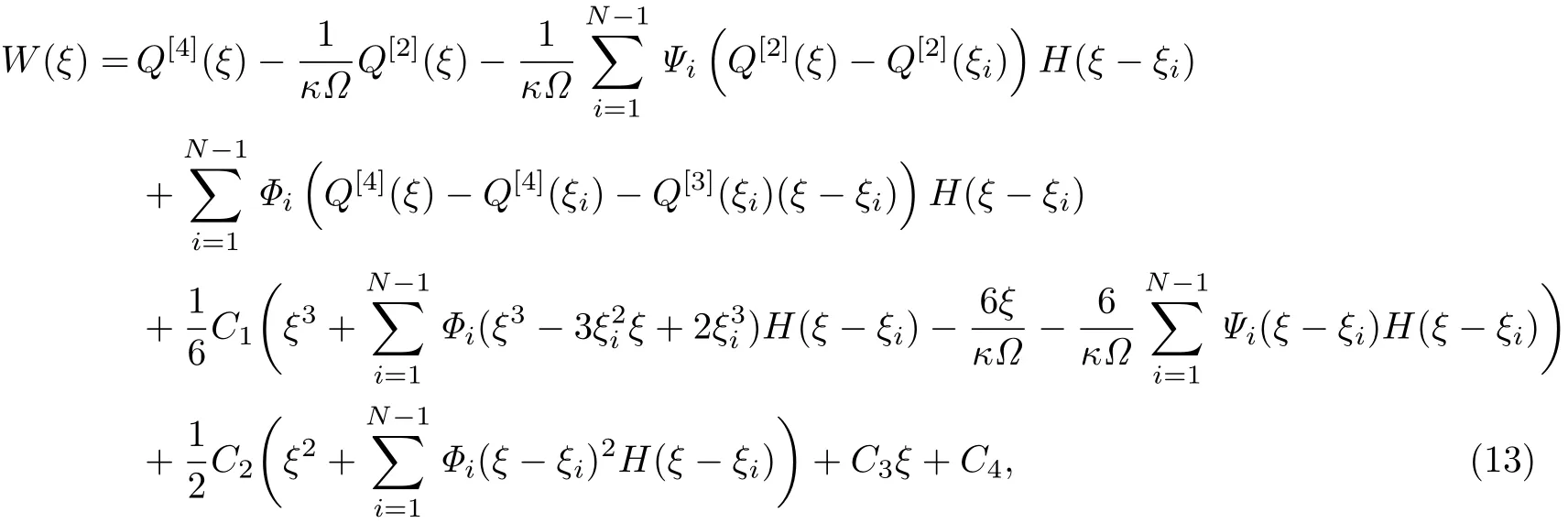
式中,C4为待定系数,且

于是,无量纲弯矩和剪力可表示为

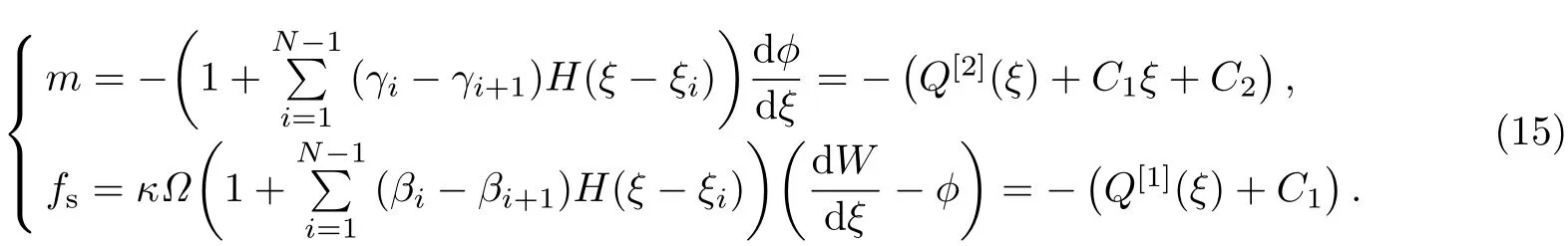
由式(6)中边界条件得到确定待定系数Ci(i=1,2,3,4)的线性代数方程组,可得

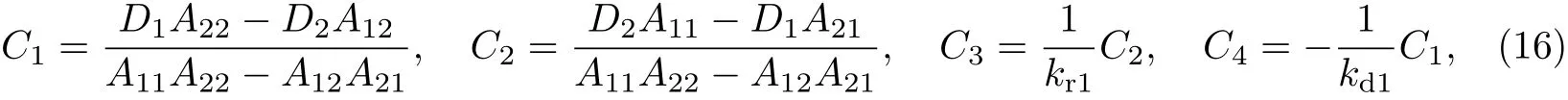
式中,

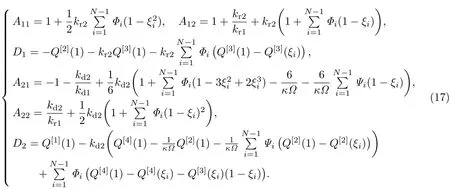
当γi=βi=0时,阶梯型截面梁退化为等截面梁.如果令Q(x)=Q,kri=kdi=∞(i=1,2),则问题变为均布载荷作用下两端固支等截面Timoshenko梁的弯曲,此时式(12)和(13)变为

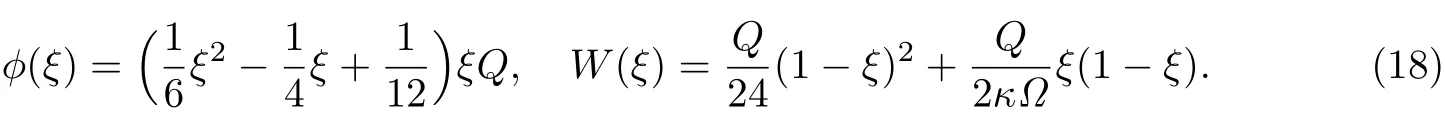
如果令kr1=kd1=∞和kr2=kd2=0,则问题变为均布载荷作用下悬臂等截面Timoshenko梁的弯曲,而此时式(12)和(13)变为

式(18)和(19)与文献[1]中的公式一致,从一个方面说明本工作推导的正确性.

2 算例分析

2.1 均布荷载下单阶梯型截面固支Timoshenko梁的弯曲

考虑长L=2 m的单阶梯型截面Timoshenko梁,即N=2,截面在x1=1 m处发生变化,且截面高度分别为h1=0.6 m和h2=0.3 m,宽度b=b1=b2=0.25 m,因此取梁弹性模量E=2×1011N·m-2,泊松比ν=0.3,剪切修正系数κ=10(1+ν)/(12+11ν)=0.85,均布荷载q(x)=q0=10 kN·m-1,且kd1=kd2=kr1=kr2=100.图2为在此工况下单阶梯型截面Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布.同时,图中亦给出了SAP2000有限元软件[22]的计算结果,可见,本工作的解析解与有限元解吻合得较好,从而验证了本工作理论公式的正确性.

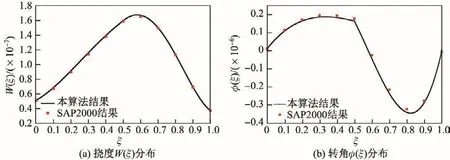
图2 单阶梯型截面Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布Fig.2 Distributions of deflection W(ξ)and rotational angle φ(ξ)of Timoshenko beam with single stepped cross-section

仍取上述单阶梯型截面Timoshenko梁的材料、几何和载荷参数,以及kd1=kd2=100.图3显示了此时边界支承无量纲扭转弹簧刚度kr=kr1=kr2对单阶梯型截面Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布的影响.可见,随着边界扭转弹性支承刚度kr的减小,梁挠度和转角增大,且在变截面ξ1=0.5处转角斜率发生明显跳跃.

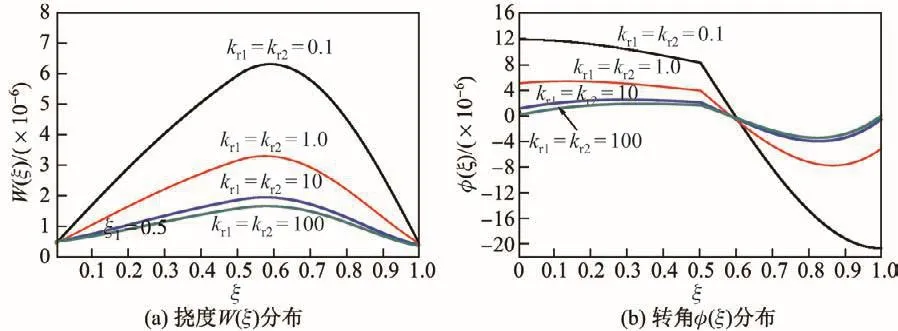
图3 不同kr时单阶梯型截面Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布Fig.3 Distributions of deflection W(ξ)and rotational angle φ(ξ)of Timoshenko beam withsingle stepped cross-section for different kr

取kd1=kd2=kr1=kr2=1010(相当于两端固支梁),除截面变化位置x1外,其他参数不变.图4为无量纲截面变化位置ξ1对固支单阶梯型截面Timoshenko梁挠度W(ξ)和转角φ(ξ)分布的影响.可见,梁的挠度分布光滑,但其截面转角在截面变化ξ=ξ1处非光滑,这是由于在截面变化ξ=ξ1处梁弯矩连续,但抗弯刚度发生跳跃,从而导致截面转角φ(ξ)的斜率,即弯曲曲率发生跳跃.由于γ2=7/8＜1和β2=1/2＜1,即子梁2的抗弯刚度和抗剪刚度小于子梁1的抗弯刚度和抗剪刚度,因此随着截面变化位置ξ1的增大,梁的整体刚度增大,从而导致随着截面变化位置ξ1的增大,挠度W(ξ)和转角φ(ξ)减小.当ξ1=1.0时,梁退化为等截面Timoshenko梁,此时挠度W(ξ)和转角φ(ξ)分别关于梁跨中是对称和反对称分布,且截面转角φ(ξ)的斜率不发生跳跃.

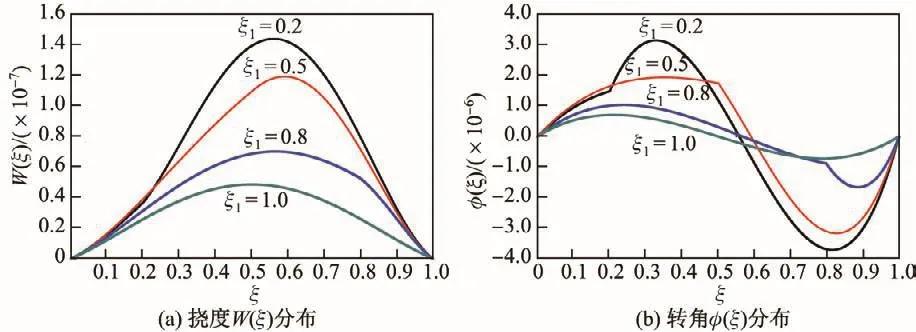
图4 不同ξ1时,单阶梯型截面Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布Fig.4 Distributions of deflection W(ξ)and rotational angle φ(ξ)of Timoshenko beam with single stepped cross-section for different ξ1

仍取kd1=kd2=kr1=kr2=1010,除h2外其他参数不变.图5显示了子梁2高度h2对单阶梯型截面固支Timoshenko梁挠度W(ξ)和转角φ(ξ)分布的影响.当h2/h1=1/3,1/2和2/3时,固支单阶梯型截面Timoshenko梁的挠度W(ξ)与固支等截面Timoshenko梁(h2/h1=1)挠度有较大的差异.随着h2/h1接近于1,即趋于等截面Timoshenko梁,其挠度W(ξ)和转角φ(ξ)趋于等截面Timoshenko梁的挠度W(ξ)和转角φ(ξ).类似地,可分析边界弹性支承条件下阶梯型截面Timoshenko梁的弯曲.

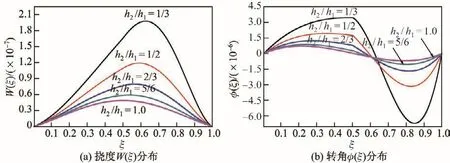
图5 不同h2时单阶梯型截面Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布Fig.5 Distributions of deflection W(ξ)and rotational angle φ(ξ)of Timoshenko beam with single stepped cross-section for different h2

2.2 均布荷载下悬臂单阶梯型截面Timoshenko梁的弯曲

为考察悬臂单阶梯型截面Timoshenko梁的弯曲变形,分别取kd1=kr1=1010和kd2=kr2=10-10,其他参数不变.图6显示了无量纲截面变化位置ξ1对悬臂单阶梯型截面Timoshenko梁挠度W(ξ)和转角φ(ξ)分布的影响.可见,截面变化位置ξ1对悬臂单阶梯型截面Timoshenko梁挠度W(ξ)和转角φ(ξ)的影响与固支阶梯型截面Timoshenko梁的相同.另外,靠近自由端的子梁截面变化并不影响固支端附近子梁的变形,即当ξ＜ξ1时其变形并不依赖于ξ＞ξ1的子梁截面的改变.

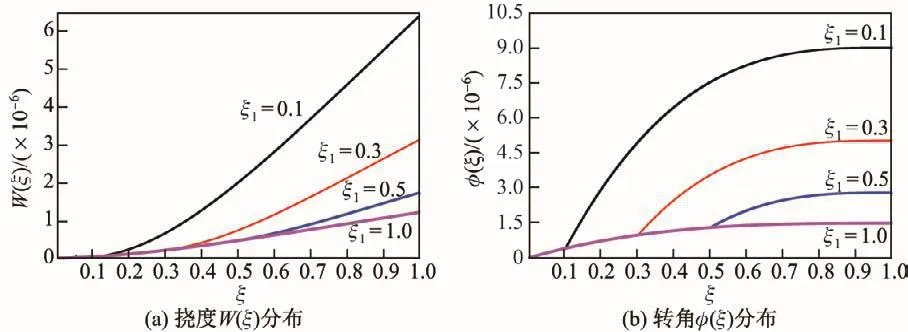
图6 不同ξ1时单变截面悬臂Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布Fig.6 Distributions of deflection W(ξ)and rotational angle φ(ξ)of cantilever Timoshenko beam with one stepped cross-section for different ξ1

2.3 均布荷载作用下固支双阶梯型截面Timoshenko梁的弯曲

考察由3个子梁组成的固支双阶梯型截面Timoshenko梁,即N=3,且取kd1=kd2=kr1=kr2=1010,材料常数不变.几何参数分别为：梁长L=1.80 m,变截面位置ξ1=1/6,ξ2=5/6,各子梁截面宽度分别为b1=0.30 m,b2=0.20 m和b3=0.25 m；一组截面高度分别为h1=0.60 m,h2=0.40 m和h3=0.5 m,记为Beam-Ⅰ,而另一组截面高度分别为 h′1=0.30 m,h′2=0.20 m 和 h′3=0.25 m,记为 Beam-Ⅱ. 图 7 分别显示了固支双阶梯型截面Timoshenko梁Beam-Ⅰ和Beam-Ⅱ的挠度W(ξ)和转角φ(ξ)的分布.可见,随着高跨比的减小,梁的挠度和转角值增大.

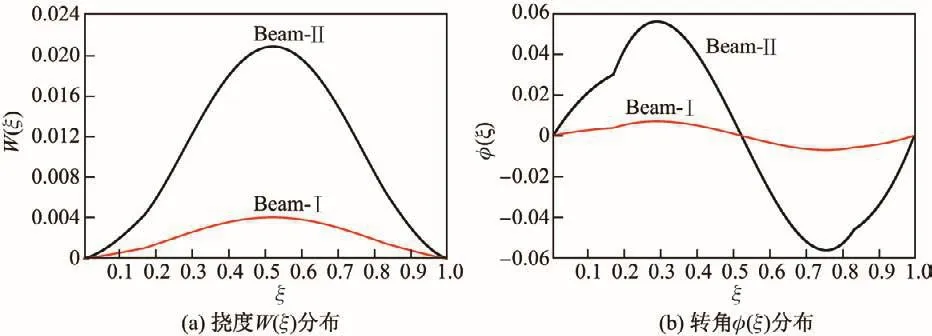
图7 固支双阶梯型截面Timoshenko梁的挠度W(ξ)和转角φ(ξ)分布Fig.7 Distributions of deflection W(ξ)and rotational angle φ(ξ)of clamped Timoshenko beam with double stepped cross-sections

3 结 论

本工作研究了边界弹性支承下任意阶梯型截面Timoshenko梁的弯曲变形.首先,利用Heaviside广义函数,给出了阶梯型截面Timoshenko梁沿梁跨的抗弯刚度和抗剪刚度；其次,由Timoshenko梁的弯曲控制方程和边界弹性支承条件,得到了阶梯型截面Timoshenko梁挠度和转角的解析闭合解.在此基础上,数值分析了固支和悬臂阶梯型截面Timoshenko梁的弯曲,考察了变截面位置、截面大小以及梁高跨比等对Timoshenko梁弯曲的影响,得到如下结论：

(1)利用Heaviside函数给出的阶梯型截面Timoshenko梁抗弯和抗剪刚度公式,避免出现经典阶梯型截面Timoshenko梁分析方法中变截面处的连续性条件,简化了计算,并给出了整个梁跨上弯曲挠度和转角的统一标准解析闭合解；

(2)阶梯型截面Timoshenko梁的挠度和转角分布与等截面Timoshenko梁的挠度和转角分布有较大的差异,在截面变化位置处阶梯型截面Timoshenko梁转角斜率存在明显的突变跳跃,且截面尺寸变化越大,转角跳跃越明显；

(3)对于悬臂单阶梯型截面Timoshenko梁,靠近自由端的梁截面变化不影响固支端附近梁的变形.