面向障碍速度不确定性的无人艇动态避碰

瞿 栋,彭 艳,蒲华燕,罗 均, 黄承义,柯 俊

(1.上海大学机电工程与自动化学院,上海200444；2.国家海洋局北海海洋工程勘察研究院,山东青岛266061)

无人艇在水面航行时需对运动船只进行规避,保证自身的航行安全.动态避碰技术是无人艇自主化程度的重要体现.然而,海面目标检测和跟踪十分困难.目前环境感知手段包括导航雷达、激光雷达、摄像机.导航雷达探测范围广,但是分辨率、探测频率较低.激光雷达分辨率较高,但是探测范围只有百米级,且易受船体颠簸的影响.摄像机能获得丰富的纹理和色彩信息,但是无法准确估计目标的方位和距离,且易受光照条件影响.另外,不同于地面无人车,船舶本身就是一个欠驱动、大惯性、强时滞的系统,航行过程中因受风浪涌流干扰导致无人艇姿态不稳,也会对无人艇传感探测造成影响.因此,在目前的技术手段下无人艇难以观测到精确的目标运动信息,使得无人艇在动态避碰过程中出现策略跳变,导致运动状态不稳定,影响航行安全.本工作将传感技术局限性导致的获得障碍物信息存在不确定性的现象,统称为障碍信息不确定性,其中障碍速度的不确定性是影响避碰成功率的关键.

针对无人艇动态避碰问题,一般有2种解决办法.一种是基于全局或者部分信息已知的路径规划方法,又称为零阶避碰方法.代表性算法包括势场法[1]、A*[2]、神经网络方法[3]等.另一种是基于行为的避碰方法,又称为一阶避碰方法,该方法能对无人艇和障碍物运动情况作出实时反应,通过改变无人艇自身运动状态实现规避动作.代表性算法包括速度障碍物[4]、动态窗口法[5]等.

针对障碍速度不确定性条件下的避碰问题,Kuwata等[6]采用速度障碍(velocity obstacle,VO)算法和国际海事避碰规则(International Regulations for Preventing Collisions at Sea,COLREGS)进行动态目标避碰,并将障碍速度不确定性融入VO区域中,建立新的VO区域,称为最差情况下的速度障碍(worst case velocity obstacle,WVO),但是并未给出WVO数学模型.Fulgenzi等[7]提出概率速度障碍法,在环境地图中将传感器检测到的目标信息以概率占据的方式进行建模,解决障碍速度不确定性对避碰过程带来的影响,该方法适用于室内移动机器人.张洋洋等[8]提出了建立4个虚拟障碍物,投射到无人艇的速度空间,模拟障碍速度不确定性对VO区的影响,该方法缺乏有效的理论支撑.杨秀霞等[9-10]以无人飞行器为研究对象,在VO算法的基础上,将动态不确定性通过威胁障碍速度矢量方向角的偏差来表示,并建立了动态不确定性VO模型,该方法未进一步对无人机速度空间中障碍速度不确定性进行建模.张成钢等[11]考虑了2个不确定性来源,即运动速度上的不确定性和运动方向上的不确定性,用概率统计的方法为不确定性建模,该方法同样适用于室内移动机器人.卢艳爽[12]用极大似然估计法计算运动障碍物航速和航向误差,依据计算结果对障碍物进行二次膨化,将不确定性转为确定性,该方法难以从根本上解决障碍速度不确定性对无人艇避碰的影响.Johansen等[13]采用模型预测控制方法,根据动力学模型及相应的控制指令计算无人艇在位姿空间中的状态,同时对障碍物的运行状态进行预测,并构建评估函数进行碰撞风险评估及控制指令择优,该方法对传感器和艇体运动的不确定性进行了考量,但是在实验过程中仍然无法避免无人艇避碰策略的剧烈跳动.Park等[14]针对运动障碍物轨迹不确定性问题,通过目标跟踪滤波器输出的估计协方差进行不确定性建模,并采用概率统计方法对碰撞风险进行计算,通过在仿真平台下避让单个/多个运动目标,验证了该算法的可行性.Larson等[15]在无人艇的二维栅格地图中将障碍物速度不确定性通过障碍物投影区(projected obstacle area,POA)的方式进行建模,采用局部路径规划的方式对含有速度不确定性的障碍物进行规避.

综上所述,目前国内外针对无人艇在障碍信息存在不确定性条件下的避碰方法研究较少,绝大多数研究尚停留在理论阶段,或者在仿真/半实物仿真状态下取得了较好的效果,但在真实应用场景下的避碰效果还有待进一步验证.本工作在已有研究基础上,提出了一种面向障碍速度不确定性的速度障碍(uncertain velocity obstacle,UVO)避碰方法,从宏观和微观两个层面解决速度不确定性条件下的避碰问题,并利用仿真和海试实验对该方法的有效性进行验证.

1 理论基础

1.1 VO原理

速度障碍法是1998年由Fiorini等[16]提出的.在北东地(north east down,NED)坐标系下,假定无人艇的位置为pA,速度为vA,障碍物位置为pB,速度为vB.无人艇加上障碍物的尺寸为r,如图1所示.

图1 速度障碍法原理Fig.1 Principle of velocity obstacle method

以无人艇的位置pA为起点,对障碍物圆作两条切线,左切线角度为λL,右切线角度为λR,如图1中绿线所示.经过障碍物的圆心pB作两根切线的垂线TL和TR.若无人艇相对于障碍物的速度vAB=vA-vB处于λL和λR之间,则将与障碍物发生碰撞.将发生碰撞的无人艇速度矢量集合称为VO,表示为

在实际应用中,对无人艇的参考速度空间进行离散化,(vi,θj)即无人艇的1个参考速度矢量(见图2),速度大小被划分为m份,速度方向被划分为n份.

1.2 最近会遇点方法

如图3所示,采用最近会遇点(closest point of approach,CPA)方法评估己方船只与其他来船的碰撞风险[17],计算2个参数即最近会遇距离dcpa和最快会遇时间tcpa,

图2 速度空间离散化Fig.2 Discretization of velocity space

式中,dcpa表示两船会遇过程中的最近距离,tcpa表示两船到达最近会遇点所需的时间,ε为设定的极小值.文献[18]在无人艇避碰中用CPA方法度量无人艇和障碍物船只的碰撞风险.将dcpa和tcpa与设定的阈值εDCPA和εTCPA进行比较,若满足式(3),则视为无人艇与障碍物之间存在碰撞风险,

图3 最近会遇点原理Fig.3 Principle of closest point of approach

1.3COLREGS

文献[19-21]将COLREGS应用于无人艇避碰中,其中在超越、对遇和右舷来船3种场景下,己方船只应从右侧避让来船；在左舷来船场景下,己方船只应保持直行,由来船采取避让措施(见图4).

对超越、对遇、左舷来船、右舷来船4种海事规则场景的定义(见图5)如下(φB表示无人艇相对于障碍物船首的方向)：

(1)超越场景,-180°＜ φB＜ -112.5°或112.5°＜ φB＜ 180°；

(2)对遇场景,-15°＜ φB＜ 15°；

(3)左舷来船场景,15°＜φB＜112.5°；

(4)右舷来船场景,-112.5°＜φB＜-15°.

图4 COLREGS场景Fig.4 COLREGS scenarios

图5 COLREGS场景判断方法Fig.5 Judgment method of COLREGS

2 不确定性条件下的速度障碍法

2.1 基于自适应阈值的CPA和COLREGS计算方法

用CPA方法计算dcpa和tcpa用于评估碰撞风险,若满足式(3),则无人艇应进入避碰状态；否则回归设定航路继续航行.因此,CPA评估结果的稳定性十分重要.然而,由于障碍速度的不确定性,导致dcpa和tcpa在设定的阈值附近波动,进而导致无人艇在避碰和回归航路2种状态之间来回切换,对艇体自身的稳定性和避碰安全性产生较大影响.

本工作采用自适应阈值的方法,将静态阈值εDCPA和εTCPA设定为动态阈值,提高碰撞风险评估结果的稳定性,

式中,ΔTcpa和ΔDcpa为设定的常数,k为自适应系数,与无人艇上一时刻的状态相关联,满足式(4),则视为当前帧存在碰撞风险.将式(4)的计算结果称为初始评估状态,设为pi.pi是一个二值化状态,0代表无风险,1代表潜在风险.为了保证避碰过程的连续性,进一步提高碰撞风险评估结果的稳定性,采用滚动滑窗法对过去一段时间的碰撞风险评估结果进行计算,滑窗中的元素为i时刻的初始评估pi.滑窗的长度选取依赖于无人艇的控制频率,本工作采用10帧.在滑窗中采用7/10法则,若过去一段时间内超过70%的时刻被判定为存在碰撞风险,则最终碰撞风险评估结果记为Ri=1,无人艇进入避碰状态；否则,无人艇退出避碰状态,记为Ri=0(见图6).

图6 滑窗方法计算最终碰撞风险Fig.6 Calculation of the final collision risk by the sliding window method

同理,由于在计算COLREGS场景的过程中以动态障碍物船首方向为参考,因此判断结果极易在4个边界角度(±15°,±112.5°)附近出现变换.本工作在以上4个边界角度附近设置4个边界缓冲区(见图7),边界缓冲区的大小为2δ,lb和rb分别为缓冲区的左边界和右边界.通过设置以上4个边界缓冲区,并且关联上一时刻无人艇的COLREGS类型,无人艇COLREGS类型切换的逻辑如表1所示,其中T表示当前时刻,T-1表示上一时刻.

图7 边界缓冲区设置规则Fig.7 Setting rules of boundary buffer

2.2 UVO数学模型

文献[6]中对障碍物不确定性条件下产生的VO区进行了阐述,新的VO区(即WVO)是一个包含原VO区的锥形.文献[9]构建了动态不确定性速度障碍模型,并运用几何法进行了推导和证明.本工作在无人艇的速度空间中对障碍物不确定性条件下的速度障碍区进行了建模,将新的VO区称为UVO(见图8).

表1 COLREGS场景切换逻辑Table 1 Switching logic of COLREGS types

图8 无人艇参考速度空间中的UVOFig.8 UVO in reference velocity space

假定障碍速度不确定性度量为ΔvB和ΔφB,对ΔvB和ΔφB进行离散处理,分别离散成N和M份,则障碍物的实际速度可以看成是一个速度集合：

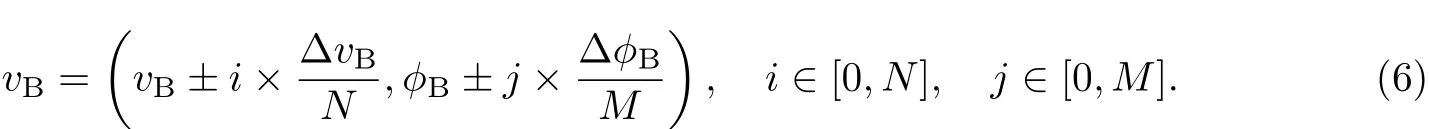
在无人艇的参考速度空间中,将障碍物的速度vB叠加到无人艇后,即可将障碍物看作是静止的.以障碍物速度大小的不确定量ΔvB为半径作圆(见图8),红圈即可等效为障碍物在速度不确定性条件下的速度集合(见式(6)).因此,可以将UVO区等效为障碍物在一个确定的速度下得到的,则障碍速度不确定性转化为确定性,

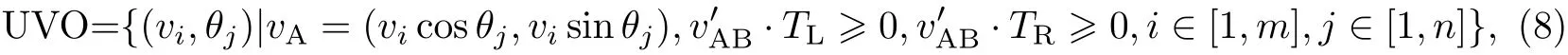
2.3 代价空间设计与策略优化

对于无人艇的参考速度空间(v,θ),需要计算每个参考矢量(vi,θj)的代价值,即评价函数J(vi,θj),该函数是一个关于v和θ的二元函数.文献[22]给出了典型的评价函数形式.本工作主要考虑以下3个因素：①是否遵守COLREGS；②是否属于UVO区；③与参考矢量的偏离程度.将违反COLREGS和属于UVO区内参考矢量对应的代价值全部置为最大代价值1,即不可行空间；然后,在其他可行空间中根据梯度下降法寻找局部最优解,避免因为寻找全局最优而牺牲了避碰策略的稳定性.

评价函数J(vi,θj)设计为

以上代价空间是一个关于(v,θ)的二元曲面,采用梯度下降方法,从代价空间中选取一个初始点(vi,θj)作为中心点,同时向4个方向进行搜索,得到4个备选点(vi-1,θj),(vi+1,θj),(vi,θj-1),(vi,θj+1),分别计算4个点的梯度值,选择梯度下降最快的点作为第二次迭代的中心点,再次向4个方向搜索.以(vi,θj)向(vi,θj+1)搜索为例,梯度值

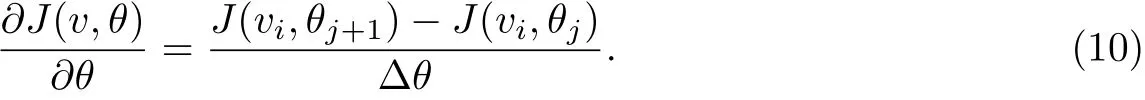
重复以上过程,则经过N次迭代,若满足某点向任意方向搜索得到的梯度值均小于所设定的阈值Δthre,搜索过程结束,该点即为代价空间中的一个局部极小值点.将该极小值点对应的(vi,θj)作为最佳避碰策略.每次迭代过程都将上一时刻的最佳避碰策略对应的矢量(v,θ)作为当前时刻梯度下降法搜索的初始点,这样就保证了前后2帧之间的输出策略尽可能相似,避免了由于避碰策略的急剧变化而导致的无人艇运动的不稳定性.

3 仿真与实验

3.1 仿真平台对比

为了验证本工作提出的UVO算法相比于VO算法具有更好的稳定性,在仿真系统中设置相同的实验场景和参数,对2种算法进行对比分析.在仿真过程中,设置对遇、左舷来船、右舷来船、超越4种场景,每种场景下VO算法和UVO算法各运行10次,共计40次.统计无人艇在避碰过程中的3个重要指标.

(1)避碰策略跳动次数Nc,前后2帧避碰角度变化超过20°视为1次策略跳动,该指标直观反映避碰策略的稳定性,跳动次数越少越稳定；

(2)避碰成功率Ps,即成功避碰次数/总实验次数；

(3)与障碍物的最近会遇距离dsafe,表示避碰过程中无人艇离障碍物最近时刻两船之间的相对距离.

以无人艇与障碍物对遇实验为例,对比2种不同算法下的避碰效果,如图9和10所示.

图9 避碰轨迹对比图Fig.9 Comparison of the trajectory in collision avoidance

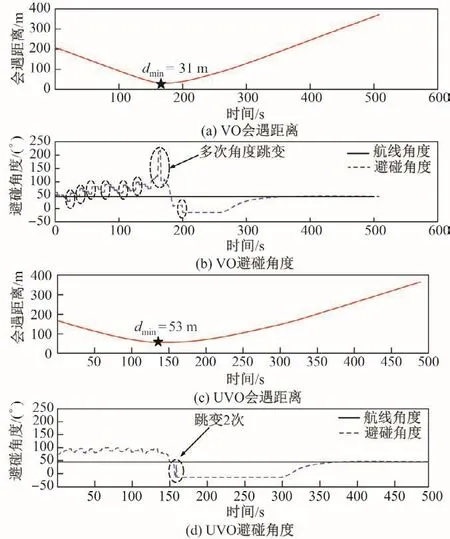
图10会遇距离和避碰角度对比Fig.10 Comparison of safe distance in collision avoidance and collision angle

图9 为2种算法对应的避碰轨迹,可见VO算法和UVO算法均能有效避开障碍物.图10为2种算法对应的避碰角度和会遇距离变化,可见UVO算法的避碰角度更加稳定,前后2帧之间跳动很小,只在避碰结束时产生了2次达到20°以上的跳动,而VO算法则有明显的角度跳动产生,达到8次.从最近会遇距离曲线的对比也能看出,UVO算法(53 m)优于VO算法(31 m).将40次仿真的结果进行统计,结论如表2所示.

表2 仿真结果统计Table 2 Statistical data of simulation results

从表2可以看出,在相同仿真条件下,基于多次实验结果进行统计分析,UVO算法在Nc,Ps和dsafe这3个主要指标上均优于VO算法.这是由于在仿真平台下对障碍物添加一定量的“噪声”干扰后,将在以下3个方面影响避碰过程：①开始与结束避碰的时刻；②避碰的宏观策略(无人艇从障碍物的左侧还是右侧规避)；③避碰的微观策略(无人艇以多大角度对障碍物进行规避).而本工作提出的UVO算法是基于以上3个关键点对CPA,COLREGS和VO算法进行改进,从而尽可能降低障碍速度不确定性对无人艇避碰过程的影响,保持艇体运动的稳定性.另一方面,从dsafe这项指标可以看出,UVO算法相比于VO算法绕行距离更远,如图9所示.这是由2.2节所述UVO算法的数学模型决定的,UVO算法的本质就是将障碍速度的不确定性通过扩大VO区的方式映射到无人艇的速度空间中,从而损失了更多的可行空间,但是对于无人艇的安全航行具有重要意义.

3.2 典型运动场景避碰实验

为了进一步验证本工作所提UVO算法的有效性,以上海大学“精海3号”无人艇为实验平台,采用激光雷达作为环境感知的主要手段[23],以有人驾驶辅助艇作为障碍物,在山东青岛某港口进行了真实环境下的避碰实验(见图11,关注“上海大学学报自然科学版”微信公众号,使用菜单栏“小程序”扫描左图观看视频).

图11 “精海3号”无人艇Fig.11 “JingHai-3” unmanned surface vessel

本实验设计了左舷来船、右舷来船、对遇、超越4种典型会遇场景.图12为4种场景下的避碰过程.实验结果表明：①在以上4种典型会遇场景下,无人艇均能有效避开运动障碍物,避碰结束后继续回归航迹线航线；②在实验过程中,单次实验的平均避碰策略跳动次数为1次,避碰过程平稳；③在4组实验中,无人艇与障碍物最近会遇距离的平均值为44.6 m,避碰

图12 4种典型会遇场景下的避碰实验Fig.12 Four types of collision avoidance experiments under typical encounter scenarios

过程安全.通过无人艇实艇海试,验证了本工作所提UVO算法的有效性.实际上,在实艇避碰的过程中,无人艇运动也存在一定的不确定性.与此同时,受到海上风、浪、涌、流的影响,无人艇运动轨迹与仿真平台下的运动轨迹也存在明显差异,表现为艇艏抖动及路径不平滑.如图12(b)和(d)所示.以上因素客观上也造成了传感器观测的不稳定,因此在实艇避碰过程中,无法完全避免避碰策略的跳动.实验结果显示以上4组避碰实验中,平均避碰策略跳动次数为小于等于1次.本工作提出的UVO算法通过牺牲时间和效率换取避碰策略的稳定性,在一定程度上能够避免避碰策略的频繁跳动.未来,还需结合传感器观测和无人艇运动控制两方面因素共同解决障碍物信息不确定性条件下的避碰问题,进一步提升避碰效率,增加安全性和稳定性.

4 结束语

本工作针对无人艇动态避碰过程中由于障碍速度不确定性导致避碰策略不稳定的问题,从宏观和微观两个尺度上基于VO算法进行改进,仿真对比和实艇实验验证了本工作提出的UVO算法具有较好的稳定性、安全性和有效性.无人艇的避碰性能未来还有很大的提升空间,在现有的技术手段下,首先要解决的问题是提高传感观测信息的准确性和稳定性；其次,是融合一阶和二阶避碰方法,从航路规划的层面解决运动障碍物的规避问题；最后,在避碰方法中加入人工驾驶的经验和方法,提升避碰手段的智能化程度.