基于改进高斯滤波与加权环境参数自适应估计的定位方法
2019-10-31杨晔晨胡越黎承文龙郁怀波
杨晔晨, 胡越黎,3, 徐 杰, 承文龙, 郁怀波
(1.上海大学微电子研究与开发中心,上海200444;2.上海市电站自动化技术重点实验室,上海200444;3.上海大学机电工程与自动化学院,上海200444)
由大量无线传感器(wireless sensor network,WSN)节点所组成的WSN网络可应用于国防军事、环境检测和预报、医疗护理、智能家居、建筑物状态监控等诸多领域[1].当今,鉴于多媒体及数据业务的蓬勃发展,人们对于在室内环境中,如地下矿井、仓库、大型超市、停车场、机场、医院等,需要对终端设备以及持有设备的人员、物品等在室内环境中的位置进行了解.在此背景下,由于基于WSN的定位技术具有成本相对较低,无需额外布线,并能及时准确获得大量的节点信息并实现高可靠性的无线数据传输的特点,因此基于WSN的定位技术已然成为目前重要的研究方向.
基于WSN定位技术的定位算法一般分为2种:基于测距的定位算法与非基于测距的定位算法[2].基于非测距的定位算法主要有质心算法、APIT(approximate point-in-triangulation test)算法、DV-hop(distance vector-hop)算法以及无定型算法等[3].这种定位算法不需要对移动节点和参考节点之间的距离进行测量,而是利用网络的连通度来对移动节点和参考节点之间的距离或移动节点的坐标进行估算.基于测距的定位算法主要有基于到达时间(time of arrival,TOA)算法、基于到达时间差(time difference of arrival,TDOA)算法、基于信号到达角度(angle of arrival,AOA)算法以及基于接收信号强度指示(received signal strength indication,RSSI)算法等[4].这种定位算法首先对移动节点和参考节点之间的距离或者角度信息进行测量,然后利用三角质心算法、加权质心算法[5]或者三角测量算法等对移动节点的坐标进行估算.由于WSN节点一般都具备RSSI值的测量功能,因此实现基于RSSI的定位算法的成本相对较低.但是由于RSSI值会受到来自多径效应、障碍物、绕射等[6]环境因素的影响,且在不同的环境下对应不同的无线信号传播模型及模型参数(也称为路径损耗模型与路径损耗模型参数,即环境参数),因此针对不同的环境,有必要对RSSI值进行适当的滤波处理,并重新估算出不同环境下的环境参数,以建立新的路径损耗模型.
在RSSI值处理方面,杨宁等[7]采用了一种改进的高斯卡尔曼滤波算法,这种算法首先利用高斯滤波剔除一些异常值,再利用卡尔曼滤波使RSSI数据平滑输出,该算法虽能够明显降低测距误差,但会带来比较大的计算开销.陶为戈等[8]采用一种混合滤波算法,该滤波算法对均值滤波、中值滤波以及高斯滤波的结果取均值作为最终的滤波结果,这种算法虽然能够降低滤波结果的最大偏差,但是由于当RSSI值波动较大时,均值滤波以及中值滤波的滤波效果并不理想,因此当RSSI值波动较大时,将3种滤波的结果取均值可能会使滤波结果的误差变大.在环境参数的估计方面,朱明辉等[9]利用传统的线性回归方法对环境参数进行估计,这种方法虽然能取得不错的效果,但是需要提前去待测环境中采集数据,而且如果待测环境占地面积相对较大,就会消耗大量的人力与物力.李瑶怡等[10]将待定位节点所在最小定位区域中的3个参考节点进行相互协作,分别估算出3组环境参数,然后再通过对这3组环境参数取均值,以获得在该最小定位区域下的环境参数,这种算法虽然解决了文献[9]需要提前去现场采集大量数据的弊端,但是这种算法对于估算出的3组环境参数仅仅做了相同权重的处理,并没有考虑各参考节点与移动节点之间的距离对于环境参数的影响力的大小.
针对上述问题,本工作提出了一种基于改进高斯滤波与加权环境参数自适应估计相结合的定位方法,该算法利用改进高斯滤波算法对接收的RSSI值进行处理,并利用加权环境参数自适应估计算法对当前待定位的移动节点所在位置的环境参数进行估计.该算法首先对移动节点所在的最小定位区域进行判断;然后利用最小定位区域内的4个参考节点来估算出每个参考节点相对于该最小定位区域的环境参数;再利用算出的4组环境参数估算出移动节点到每个参考节点之间的距离,并以此作为依据来计算每组环境参数的权值,利用加权处理之后的环境参数重新计算移动节点到各参考节点之间的距离;最后根据三角质心定位算法来估算移动节点的位置.本工作将上述改进方案在基于CC2530的ZigBee平台上进行了验证,实验结果表明,该方法能够有效提高系统的定位精度.
1 RSSI测距模型
基于RSSI的测距通常采用无线信号传播路径损耗模型[10]中的Shadowing模型[11](或称为对数距离路径损耗模型),其表达式为

式中:d0为参考距离,一般取1 m;p0为经过参考距离d0时接收到的信号强度;d为发射节点与接收节点之间的距离;ζ是均值为0,均方差为σ的高斯随机变量;p为接收信号强度;n为路径损耗指数[12],表示路径损失随着距离的增加而增大的快慢,该值依赖于环境.在实际测量中,通常选用如式(2)所示的模型:

式中,A为射频参数,被定义为距离发射节点1 m处所接收到的平均能量(dBm),也就是距离发射节点1 m处的接收信号强度.
由式(2)可以推出,距离的估算式为

由式(3)可知,影响定位测距精度的因素有3个,首先是环境参数A和n,其次就是RSSI值.
2 RSSI值的校正
由于在实际环境下,反射、多径传播、背景干扰等因素会对无线信号的传输产生一定程度上的影响,从而使RSSI值不太稳定,因此在实际应用中需要对接收到的多个RSSI值进行滤波优化,从而满足测距与定位的需求.目前比较常用的数字滤波算法有均值滤波、高斯滤波等,本工作在这些常用滤波算法的基础上,提出了一种改进高斯滤波算法.
2.1 均值滤波
均值滤波指的是将接收到的一组RSSI值进行算术平均值的计算,并将该平均值作为测量结果.当样本数n较大时,能够较好地解决RSSI数据随机性的问题,但是当RSSI的波动范围比较大时,使用该方法估算出的RSSI值的可信度下降.
2.2 高斯滤波
鉴于大量的随机变量都近似服从正态分布,因此在接收到的一组RSSI值中,某些数值就必然是小概率事件,而大部分的数值应该会在合理的区间内波动,这样利用高斯滤波能够筛选出这些大概率的数值.
首先定义高斯函数:

式中,
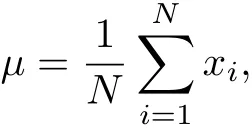
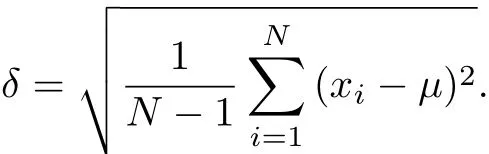
根据高斯分布,在区间[μ-δ≤RSSIi≤μ+δ]中的概率为

由上述计算结果可知,区间[μ-δ,μ+δ]为高概率发生区.通过高斯滤波筛选出在满足该高概率发生区中的RSSI值,然后对筛选出的RSSI值取平均值,得到RSSI的最终估算值.高斯滤波能够在一定程度上减少RSSI值在实际测试中由于稳定性差且易受干扰等所带来的影响.
2.3 一种改进的加权高斯滤波
当WSN网络的资源相对有限且RSSI值的样本数不多时,上述的滤波方法存在的普遍问题是当扰动较大时,样本中的异常值会对整个样本的均值以及方差造成较大的影响.因此,本工作提出了一种基于权值的改进高斯滤波模型,该滤波模型的处理过程如下:
(1)首先将接收到的一组RSSI值进行高斯滤波,在这里记高斯滤波的结果为
(2)将经过高斯处理后筛选出的RSSI值(假设有N个)分别与求差,并将差值求平方:
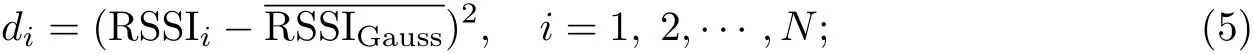
(3)计算出基于式(5)的加权系数:
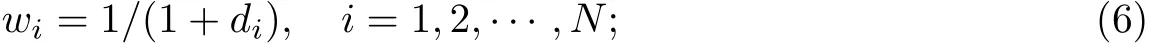
(4)最后计算出该组RSSI值最终的滤波结果为

由式(5)~(7)定义的滤波模型具有算法过程简单、易于编程实现、处理时间短的特点,并保留了高斯滤波对于抗干扰方面的优势,同时该滤波模型还对经过高斯处理之后的RSSI值分别赋予不同的加权系数,进一步提高了最终得到的数据的可信度.本工作采用该滤波模型来对RSSI值进行校正.
3 环境参数的优化
为了使测距模型能真实地反映出当前待测室内环境中的信号传播特性,以保证RSSI测距的精度,首先需要面对的一个问题就是射频参数A和路径损耗指数n的取值问题.由于A与n不同的取值会对测距的误差产生很大的影响,因此需要对A与n的取值进行优化并得到最适合当前环境的参数值.由于文献[10]并没有考虑到环境参数会随着位置的改变而改变,因此本工作针对文献[10]中提出的一种环境参数自适应估计算法(即环境参数类质心自适应估计算法),提出了一种改进的加权环境参数自适应估计算法.
3.1 环境参数类质心自适应估计算法
环境参数类质心自适应估计算法的基本思想如图1所示.图中M为待定位的移动节点,三角形abc的3个顶点为距离M相对比较近的3个参考节点,其中a,b,c 3个参考节点之间互相都能够通信,其之间距离分别为dab,dac与dbc.由于a,b,c 3个参考节点之间同处于一个相对较小的范围内,因此可以认为参考节点之间的信号传输特性和参考节点与待定位的移动节点之间的信号传输特性近似相同,即能够利用已知的3个参考节点的位置来估算出该区域的环境参数A和n.
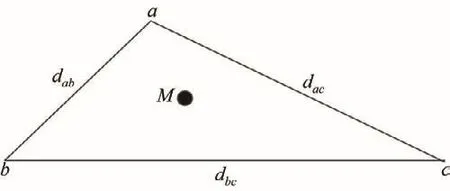
图1 环境参数类质心自适应估计算法Fig.1 Adaptive centroid-like estimation algorithm for environmental parameters
当参考节点a向b,c 2个参考节点发射信号时,参考节点b,c接收到的RSSI分别为Rba,Rca,根据式(2)建立方程组:

通过以上方程组,可以分别解得Aa,na:

同理,也可以分别得到b,c相对的参数Ab和nb,Ac和nc.于是就可以得到该区域的环境参数A和n.

通过这2个参数就可以确定在该三角形abc区域中的路径损耗模型,那么可以通过从待定位的移动节点所获取的对应的参考节点所发送过来的信号的RSSI值,来估算出待定位的移动节点和对应的参考节点之间的距离,最后再根据三角质心定位算法来估算该移动节点的位置.
3.2 一种改进的加权环境参数自适应估计算法
改进的参数优化算法的基本思想如图2所示.首先在上述算法的基础上再增加一个参考节点d,即四边形abcd的4个顶点为距离M 相对比较近的4个参考节点,其中a,b,c,d这4个参考节点之间互相都能够通信,其之间距离分别为dab,dac,dad,dbc,dbd以及dcd.
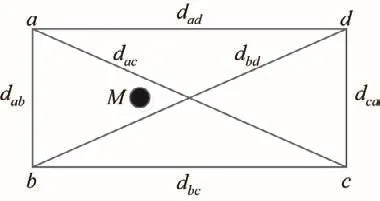
图2 加权环境参数自适应估计算法Fig.2 Adaptive estimation algorithm for weighted environment parameters
当参考节点a向b,c,d 3个参考节点发射信号时,b,c,d接收到的RSSI分别为Rba,Rca,Rda,根据式(8)建立如下3个方程组:

由式(11)定义的3个方程组,可以分别解得Aabc,nabc,Aabd,nabd,Aacd,nacd.
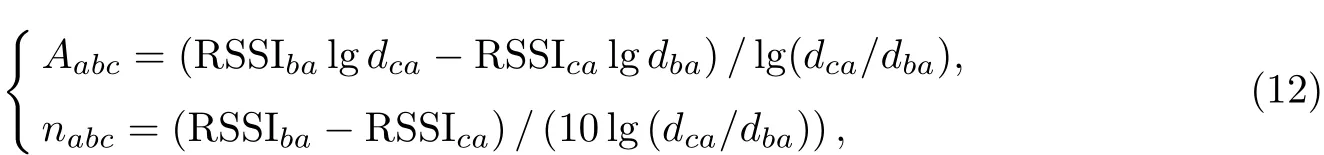
式中:Aabc,nabc代表由Rba和dba,Rca和dca这2组数据分别代入式(12)后联立得到的方程组所求得的Aa和na;同理可得Aabd,nabd和Aacd,nacd.分别通过对Aabc,Aabd,Aacd以及nabc,nabd,nacd取均值就可以得到Aa以及na:
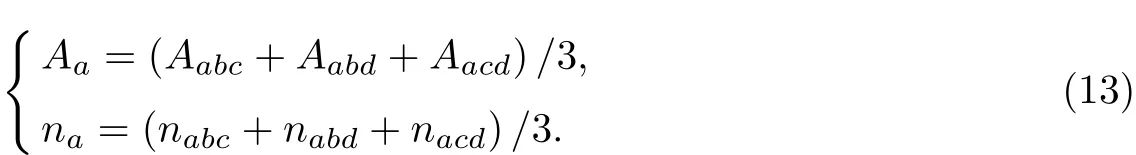
同理,也可以分别得到b,c,d相对四边形abcd区域的参数Ab和nb,Ac和nc,Ad和nd.
环境参数类质心自适应估计算法只是将参数Aa和na,Ab和nb,Ac和nc这3组参数取均值作为该定位区域的环境参数,该算法并未反映各参考节点与移动节点之间的距离对环境参数影响力的大小,而本工作提出的加权环境参数自适应估计算法能够对上述问题进行一定程度上的修正.
本工作提出的加权环境参数自适应估计算法如下.
利用上述方法分别求出Aa和na,Ab和nb,Ac和nc,Ad和nd这4组环境参数后,分别利用这4组参数计算出移动节点分别到4个参考节点之间的测量距离dij,dij代表的是利用第i组参数计算出的移动节点到第j个(这里分别用序号1,2,3,4代表a,b,c,d)参考节点之间的测量距离,对应于第k组环境参数的加权系数(通过n可以调整定位结果修正的程度,n一般取大于1的整数),因此该四边形区域中不同位置上的加权环境参数A和n的表达式为
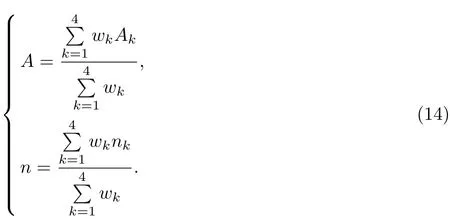
通过这2个参数就可以确定在该四边形区域中不同位置上的路径损耗模型,那么就可以通过从待定位的移动节点所获取的从对应的参考节点所发送过来的信号的RSSI值,来估算待定位的移动节点和对应的参考节点之间的距离,最后再根据三角质心定位算法来估算该移动节点的位置.
3.3 本算法的定位步骤
本算法基于2.3节提出的改进的加权高斯滤波算法,以及3.2节提出的改进的加权环境参数自适应估计算法,具体的定位步骤如下.
(1)确定待定位移动节点所在的最小定位区域:
1)初始化参考节点;
2)移动节点对请求定位的消息进行广播;
3)参考节点收到移动节点的定位请求后向其发出响应信号;
4)移动节点对收到的来自参考节点的响应信号进行比较,从中筛选出信号最强的4个参考节点参与定位.
(2)计算出移动节点在该最小定位区域中所在位置的环境参数A和n的值.
1)每个参考节点依次将接收自对应参考节点发送过来的数据的RSSI值转发给网关节点,网关节点再将接收到的RSSI值通过串口上传给上位机;当上位机接收到的各RSSI值的个数达到预定的阈值n后,上位机利用改进的高斯滤波算法对各RSSI值进行处理,得到最终的RSSI值.
2)上位机软件根据上述的环境参数估计方法,计算出该最小定位区域的4组环境参数Aa和na,Ab和nb,Ac和nc,Ad和nd.
(3)确定待定位移动节点的位置.
1)移动节点将接收自对应参考节点发送过来的数据的RSSI值转发给网关节点,网关节点再将接收到的RSSI值通过串口上传给上位机;当网关节点上传的移动节点接收到的来自对应参考节点的数据的RSSI值的个数达到预定的阈值n后,上位机利用改进高斯滤波算法对各RSSI值进行处理得到最终的RSSI值;上位机再利用加权环境参数自适应估计算法计算出移动节点当前所在位置的环境参数,并以此作为根据来估算出待定位移动节点与对应参考节点之间的距离.
2)利用三角质心定位算法计算出待定位移动节点所在坐标系中的坐标(x,y).
定位方法的流程图如图3所示.
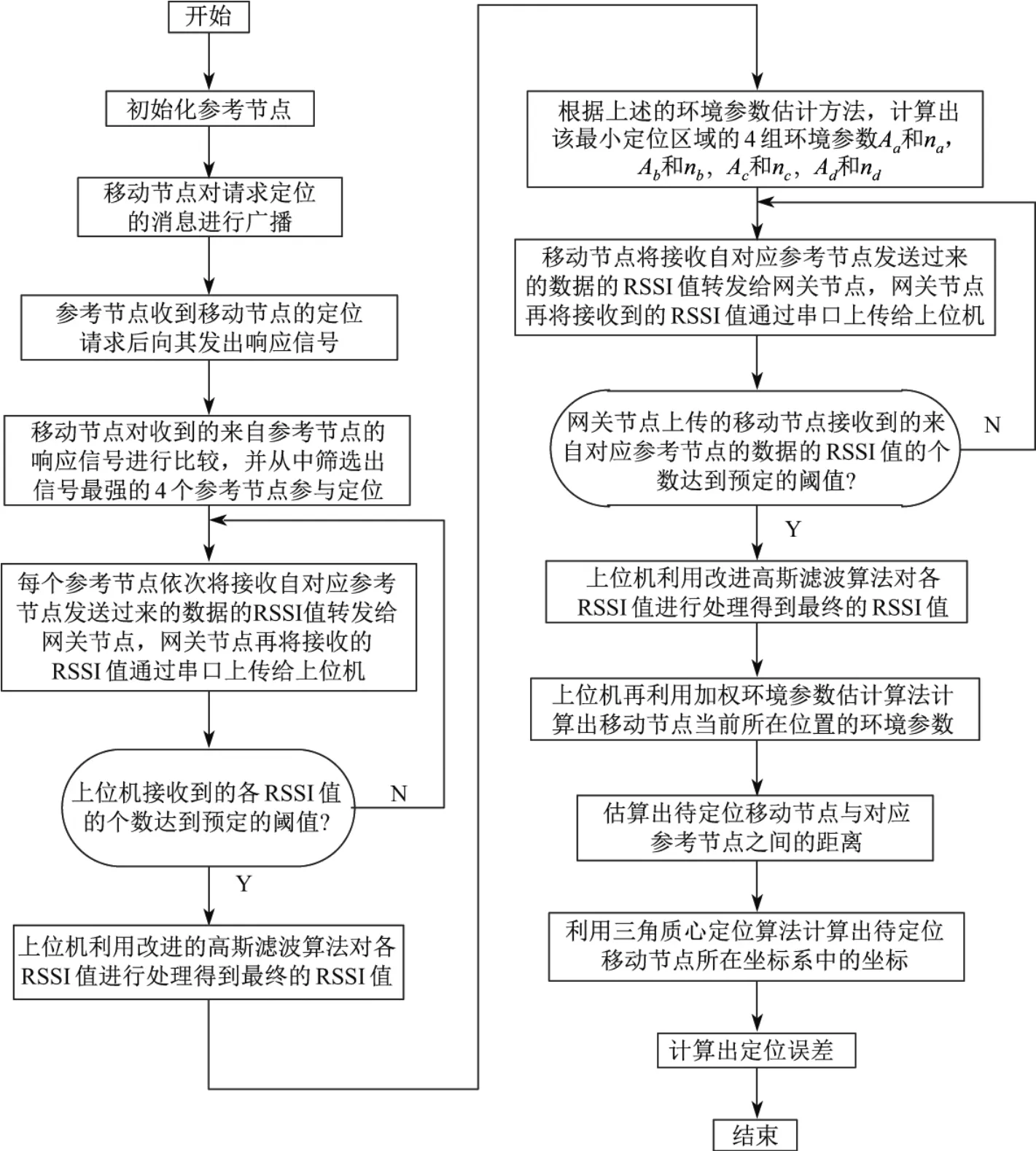
图3 定位方法流程图Fig.3 Flow chart of location algorithm
4 实 验
本实验所用的通信模块基于TI公司的CC2530芯片,上位机软件采用Visual Basic编写,上位机软件接收来自网关节点通过串口上传的信息.上位机软件具备设定移动节点的数量(支持多目标的定位)、RSSI值的采样次数、RSSI值的滤波方式、参考节点的坐标、环境参数的计算方式、实时记录移动节点的坐标、图形化实时显示移动节点的位置等功能.
本实验在室内环境中进行,在5.72m×6.00m的教室中的相同高度布置了4个参考节点进行测试,本实验对RSSI值分别采用不同的滤波算法,并结合文献[10]的环境参数类质心自适应估计算法(需要补充说明的是,由于根据文献[10]的仿真结果可知,平均定位误差会随着锚节点个数的增加而减小,因此为了能够更方便地进行对比实验,在使用文献[10]的算法时,增加一个锚节点,具体的步骤如3.2节中所述,唯一的区别是不需要如3.2节中所述的对计算出的4组环境参数Aa和na,Ab和nb,Ac和nc,Ad和nd进行加权计算,表1和图4中命名为A算法)以及本工作提出的加权环境参数自适应估计算法(表1和图5中命名为B算法)估计移动节点的位置,并在4个参考节点所包围的四边形的范围内随机选择了13个位置进行定位实验.但是考虑到天线的非方向性,故在每个位置上缓慢旋转移动节点,并在每个位置上进行多次实验取平均值作为该点的定位结果.根据文献[5]所述,一次接收10~20个RSSI值基本能满足大部分定位测距的要求,因此考虑到定位系统的实时性,将RSSI值的采样阈值设为15.表1给出了对RSSI值使用不同滤波算法时,利用文献[10]的算法与本工作提出的加权环境参数自适应估计算法时的定位误差(m)、平均定位误差(m)、最大定位误差(m)、平均改进百分比以及最大改进百分比(改进百分比是指系统使用本算法时的定位误差相较系统使用文献[10]算法时的定位误差的降低百分比).实验结果发现,改进百分比的大小随着n的增大而增大,但是当n超过10后,改进百分比的大小变化很小,因此为了减少系统的计算时间,本算法取n=10.图4是在利用文献[10]的算法时,移动节点距离坐标原点的距离增大时所对应的定位误差,图5是在利用本算法时移动节点距离坐标原点的距离增大时所对应的定位误差.
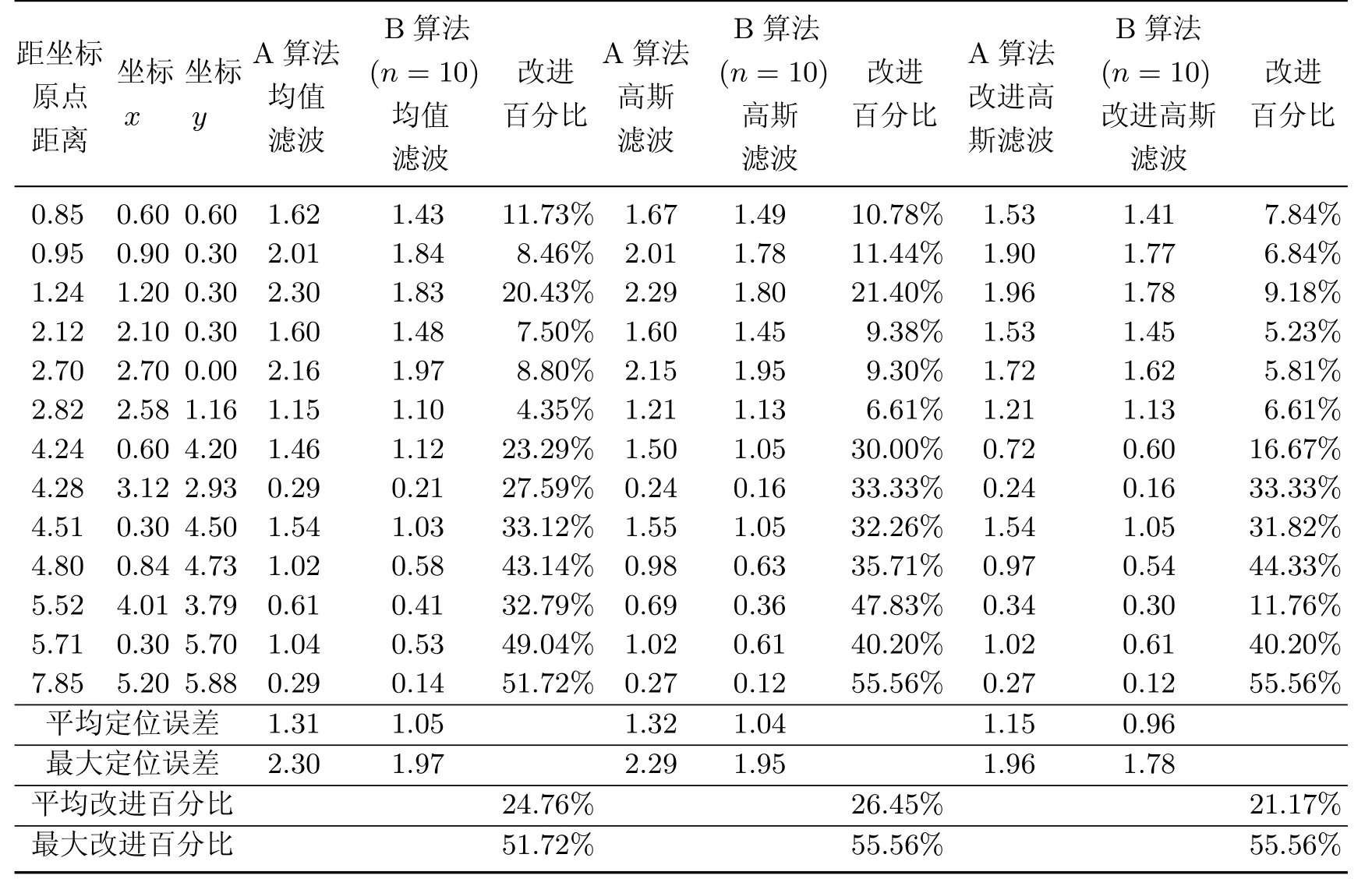
表1 定位误差比较实验数据Table 1 Experimental data of location error comparison
5 结束语
由表1中的实验结果可以看出,当系统对RSSI值使用本工作提出的改进高斯滤波算法时,对应于系统使用不同的环境参数估计算法(A算法和B算法),系统的平均定位误差分别为1.15和0.96 m,最大定位误差分别为1.96和1.78 m,小于系统对RSSI值使用均值滤波和高斯滤波时对应的平均定位误差以及最大定位误差;当系统使用本工作提出的加权环境参数自适应估计算法时,对应于系统使用不同的RSSI值滤波算法,系统的平均定位误差分别为1.05,1.04和0.96 m,最大定位误差分别为1.97,1.95和1.78 m,小于系统使用文献[10]算法时对应的平均定位误差以及最大定位误差;当系统同时使用本工作提出的改进高斯滤波算法与加权环境参数自适应估计算法时,系统的平均定位误差为0.96 m,最大定位误差为1.78 m,小于系统使用文献[10]算法并对RSSI值分别使用均值滤波、高斯滤波以及本工作提出的改进高斯滤波时的平均定位误差以及最大定位误差.对接收到的RSSI值分别使用均值滤波、高斯滤波以及本工作提出的改进高斯滤波,并使用本工作的加权环境参数自适应估计算法,可以分别使系统的定位误差平均减小24.76%,26.45%和21.17%.

图4 系统使用文献[10]算法时的定位误差Fig.4 Location errors when the system uses the algorithm of Ref.[10]

图5 系统使用加权环境参数自适应估计算法时的定位误差Fig.5 Location errors when the system uses adaptive estimation algorithm for weighted environment parameters
本工作在常规的滤波算法的基础上进行了一定的改进,提出了一种改进的加权高斯滤波算法,并在文献[10]算法的基础上提出了一种加权环境参数自适应估计算法,实验验证了本工作提出的方法的有效性.实验结果表明,本方法能够提高系统的定位精度,并且节省大量的人力与物力.本方法运算量较小,与其他比较复杂的定位方法的比较有待进一步研究.此外,本工作暂时未考虑参考节点佩戴在人身上所造成的移动节点与参考节点不在一个平面上的问题,这将是下一步需要开展的工作.
