基于IGM 和深度感知的立体图像质量评价

朱 芸,王永芳,帅 源

(上海大学通信与信息工程学院,上海200444)

由于3D图像/视频能给人以沉浸式立体体验,因此3D产品在多媒体市场中越来越吸引人们的眼球.但是由于在3D内容的捕获、压缩和传输过程中引入了不同程度的失真,降低了3D图像/视频的用户体验质量(quality of experience,QoE).因此,建立一个有效的3D体验质量评价机制来保证用户体验质量显得尤为重要.立体图像客观评价能够自动提取立体图像的特征来对图像的质量进行预测,具有快速、稳定、低物耗人耗的特点,是质量评价领域的研究热点.

现有的立体图像质量评价(stereoscopic image quality assessment,SIQA)方法模型直接将2D图像质量评价方法运用到左右视点图像上,得到相应的质量分数,然后对这2个部分的质量分数进行加权,得到立体图像的质量[1-3].但是,该方法没有考虑立体图像的特性,如深度感知、双目视觉等,与人眼感受到的立体图像质量有很大差异.在2D图像评价方法的基础上,You等[4]提出了图像质量和视差图像非线性组合的立体图像的质量；Benoit等[5]加入了视差信息,用2D图像质量评价方法C4[6]计算左右视点图像的质量,用基于结构相似度(structural similarity index model,SSIM)的方法计算视差图的质量,并将这2个部分质量融合成为最终的立体图像的质量；Yang等[7]通过计算绝对视差与传统的2维图像质量评价方法相结合的方法计算立体图像的质量.以上方法虽然考虑了视差信息,但是模型的精确度依赖于视差估计算法,比较精确的视差估计算法会大大增加计算时间,因而这种算法无法应用在实时视频质量评估中.

Shao等[8]通过训练,由立体图像的单目视觉特征得到了双目视觉特征,实验表明这些特征能有效地计算双目感知质量；Chen等[9]提出了一种基于双目融合特性的立体图像质量评价方法,该方法用Gabor滤波器作为权值响应因子,将左右图像进行双目融合生成中央眼图,将计算出的质量作为立体图像的质量；Bensalma等[10]通过模拟双目简单和复杂细胞的信息处理过程,建立了基于双目能量差异的立体图像评价模型；Galkandage等[11]扩展了基于双目能量差异的评价方法,将双目抑制等视觉特性加入到评估模型中；Wang等[12]从单个视点的质量出发,结合双目抑制特性进行3D质量评估.人类的视觉特性非常复杂,还需要进一步研究.

本工作从图像质量和深度感知质量2个方面来评估立体图像的体验质量,对于图像质量,根据人类视觉系统的内在推理机制(internal generative mechanism,IGM),将左右视点图像分别分解成可预测部分和不确定部分.对于可预测部分提出采用基于灰度共生矩阵(gray level co-occurrence matrices,GLCM)的质量评估方法；对于不确定部分提出采用基于视觉信息量的评估方法；对于深度感知质量,则采用一种改进的自然场景统计(natural scene statistics,NSS)模型来预测这部分质量.最终,将图像质量和深度感知质量融合为立体图像的体验质量.

1 基于IGM和深度感知的立体图像评价算法

本工作提出的算法流程图如图1所示,用图像质量和深度感知质量2个因素来衡量立体图像的体验质量.对于图像质量,根据自由能量理论和大脑的内在推理机制[13]可知,大脑会对输入的信息进行分析,结合已有的先验知识对信息进行推理和解读,并且忽略无序的、不可预测的信息.由此,可将立体图像左右视点分别分解成可预测部分Ip和不确定部分Iu.可预测部分包含了图像的主要信息,采用基于灰度共生矩阵的质量评估算法；不确定部分包含了无序的、不可预测的信息,采用基于视觉信息量的评估方法.对于深度感知质量,采用一种改进的自然场景统计模型对其进行评估.最后,将图像质量和深度感知质量融合成立体图像体验质量.

本工作参照文献[13]的基于贝叶斯预测理论的AR模型来推理出图像的主要内容.该方法通过周边像素χ={x1x2···xn}来预测当前像素x,计算方法为i∈χ

式中：为x的预测值,I(x；xi)为x与周边像素的互信息；为归一化系数；ε为随机噪声,这里将χ块的大小设为37×37.将输入图像分解成如图2(b),(c)所示的2个部分.

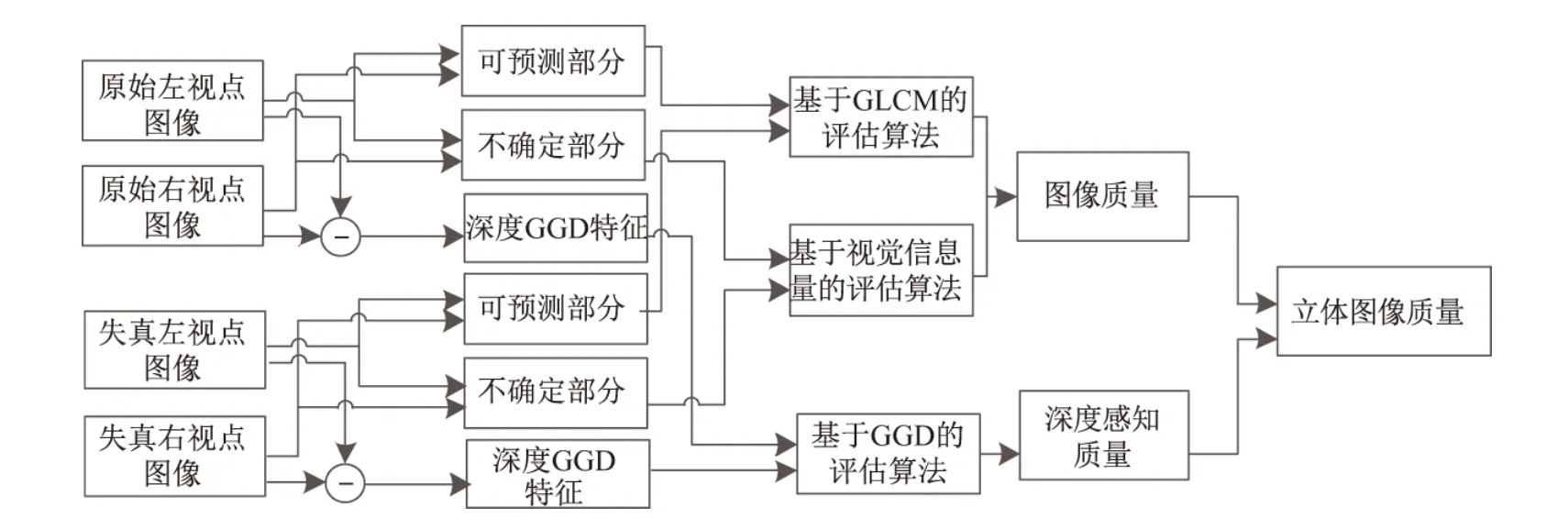
图1 算法流程框图Fig.1 Framework of the proposed approach

图2 图像分解结果Fig.2 Result of the picture decomposition

1.1 基于灰度共生矩阵的可预测部分质量评估

根据自由能量理论和人类视觉系统的内在推理机制,立体图像的可预测部分包含了图像的主要信息,这部分信息受损会影响人对图像内容的理解.GLCM是一种通过研究灰度图像的空间相关性来描述图像特征的方法.图像结构的破坏必然会使图像的空间相关性遭到破坏,因此可以利用GLCM计算可预测部分的质量.

一幅灰度级为n的图像的GLCM是一个n×n的矩阵[14],其元素为p(i,j|d,θ),表示距离为d、角度为θ的2个像素灰度级为i和j的概率.通常不直接将灰度共生矩阵作为图像特征进行分析,而是用其特征量来进行的,这些特征量可以表示图像的某些特性.在本工作中,提取的特征量如下.

(1)角二阶矩(angular second moment,ASM).

ASM反映了灰度分布均匀程度和纹理粗细程度,ASM的值越大,表示图像的纹理分布越规则,

式中：p(i,j|d,θ)是GLCM中的元素；i,j为元素的位置；d,θ为灰度图像中2个像素之间的距离及角度,这里d=1,θ =0°,45°,90°,135°.

(2) 信息熵(entropy difference,END).

END描述了图像的信息量,GLCM的信息熵描述了图像的纹理的密集程度,END的值越大,图像的纹理越趋于平坦,

(3)对比度(contrast,CON).

CON表示局部图像的变化程度,代表纹理的锐化程度.当图像边缘尖锐、有较深的纹理沟槽时,该值较大,

(4)相关性(correlation,COR).

COR表示图像灰度的局部相关性,

对原始立体图像左右视点和失真立体图像左右视点的可预测部分,分别提取以上4个特征量F=(ASM,END,CON,COR),表示为通过原始图像和失真图像的特征量的相似度来衡量图像的质量(以左视点为例)：

式中：C1为常数,C1=(0.03L)2,保证分母不为0；L为灰度级.

为了提取图像在多个尺度上的失真情况,本工作将图像转化成3个不同灰度级的灰度图,得到3个GLCM(4×4,8×8,16×16),一共得到3个相似性度量相似地,对于右视点也得到3个相似性度量那么可预测部分的质量即为

式中,ω1,ω2,ω3为权重系数,调整各部分的重要性.

1.2 基于视觉信息量的不确定部分质量评估

图像的不确定部分包含较多无序信息,该部分独立于图像的主要视觉信息,信号的能量直接表示内容的不确定度[15],即视觉信息量.由此,不确定部分的质量采用基于视觉信息量的质量评估算法.不确定部分的信息量表示为

式中,Iu为图像的不确定部分,N为图像总的像素数目.

对于原始、失真立体图像的左右视点的不确定部分,分别计算视觉信息量得到左视点的不确定部分的质量为

由人眼双目视觉和视觉信息量之间的关系[16]可知,在双目感知过程中,对立体图像的质量感知由含有较多信息量的视图决定.因此,立体图像不确定部分的质量为

1.3 基于自然场景统计的深度感知质量评估

立体图像左右视点的差值图表示物体的轮廓,也是立体图像中视差变化剧烈的地方,一旦这些位置发生失真,就会使物体的深度感下降,从而降低立体图像的感知质量.因此,本工作对立体图像左右视点作差,并利用自然场景统计模型提取统计参数,根据统计参数的变化衡量图像的深度感知质量.通过实验发现,归一化差值图并不能很好地拟合成统计模型,如广义高斯模型(generalized Gaussian distribution,GGD),故利用梯度幅度对归一化差值图进行校正.

把左右视点差值记为ΔI,将其归一化[17]：

校正后的归一化差值为

校正后的归一化差值满足广义高斯分布：

1.4 立体图像质量评估

立体图像的体验质量包括多方面的因素,不仅要考虑图像质量,还要考虑立体效果、舒适度等.对图像的可预测部分和不确定部分的质量进行融合,作为图像质量[13],结合深度感知质量融合为最终的立体图像体验质量[18]：

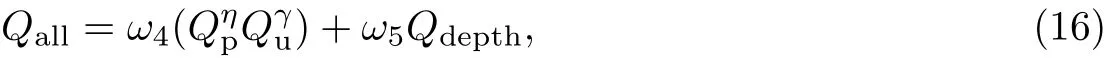
式中,Qp为可预测部分的质量,Qu为不确定部分的质量,为深度感知质量.联立式(8),(16),由BFGS(Broyden-Fletcher-Goldfarb-Shanno)优化算法[19]获得误差最小时的参数值,ω1=0.15,ω2=0.7,ω3=0.15,ω4=0.85,ω5=0.15,η =0.75,γ =0.25.

2 实验结果

本工作在Waterloo-IVC 3D PhaseⅠ[20],PhaseⅡ[21]以及Live 3D PhaseⅡ[22]图像库上对所提算法的有效性进行验证.以上3D图像库都含有对称失真和非对称失真的立体图像,特别是Waterloo-IVC 3D图像库,含有不同失真类型、不同失真程度的2个视点的组合.

在实验过程中,将图像库中80%的图像作为训练集,20%作为测试集.模型中的系数由训练得到,然后用训练好的模型对余下的20%的图像进行测试.本工作用2个常用的指标来衡量模型的性能,分别是皮尔逊线性相关系数(Pearson linear correlation coeきcient,PLCC)和斯皮尔曼秩排序相关系数(Spearman rank order correlation coeきcient,SROCC).这2个系数越趋近于1,那么这个模型的性能就越好.

为了验证模型的有效性,将本算法与其他现有的算法进行比较,这些算法分别为加入视差线索的文献[4-5,7],以及加入双目视觉特性的文献[8-9,11-12].结果记录在表1～3中,其中性能最好的2个算法的结果用黑体标出.由表1～3可见,本算法在这3个图像库中都具有较好的性能.在Live 3D PhaseⅡ数据库上,本算法的性能在对称和非对称失真的图像中都与主观评分有较高的一致性,且PLCC和SROCC都达到了0.9以上.虽然文献[9]对称失真数据库中的性能较好,但是在非对称失真数据库中的性能不如本算法.文献[12]在表2和3中的非对称失真评估性能不如本算法,且其算法需要原始图像,而本算法不需要任何参考图像,在精确度和带宽上有更好的权衡.在这2个数据库中,基于视差图的算法的性能都比较差,这是因为视差图的获得不能做到很精确,易造成实验结果有偏差.基于双目视觉的算法在不同的失真情况下更具有稳定性,但总体上在对称失真的情况下性能更好.本算法在不同数据库中的实验结果都比较稳定,且都具有较好的性能.

表1 不同算法在Waterloo-IVC 3D PhaseⅠ数据库中的性能对比Table 1 Performance of different methods on Waterloo-IVC 3D Phase Ⅰdatabase

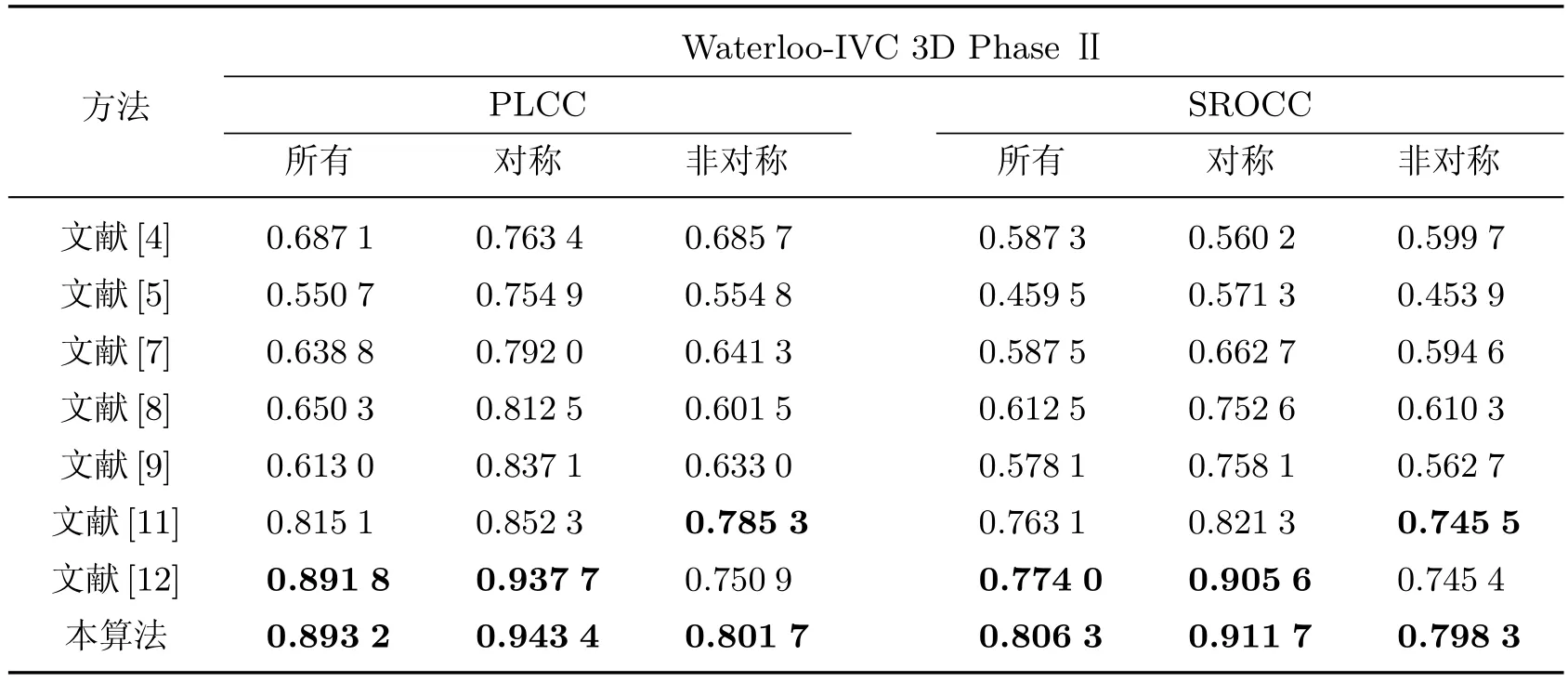
表2 不同算法在Waterloo-IVC 3D PhaseⅡ数据库中的性能对比Table 2 Performance of different methods on Waterloo-IVC 3D Phase Ⅱdatabase

3 结束语

本工作提出了一种基于大脑内在推理机制和深度感知的立体图像评价算法.根据大脑的内在推理机制,本算法将左右视点分别分解为可预测部分和不确定部分,其中对可预测部分采用基于GLCM的质量评估算法,对不确定部分采用基于视觉信息量的质量评估算法.本算法加入了深度线索,用改进的基于NSS的模型评估深度感知质量.最后,将以上3个部分的质量融合为立体图像的感知质量.在Waterloo-IVC 3D和Live 3D PhaseⅡ数据库中的实验结果表明,本算法优于现有的立体图像质量评估算法,与主观感受具有较高的一致性.下一步的研究工作是对人眼视觉系统的特性做进一步的研究,并提取相应的特征以提高立体图像质量评估算法的性能.

表3 不同算法在Live 3D PhaseⅡ数据库上的性能对比Table 3 Performance of different methods on Live 3D Phase Ⅱdatabase