光聚Rayleigh 粒子射流

牛振宇, 周哲玮, 黄 凯, 张金松, 张建华, 王志亮

(1.上海大学上海市应用数学和力学研究所,上海200072；2.上海大学上海市力学在能源工程中的应用重点实验室,上海200072；3.上海大学机电工程与自动化学院,上海200444；4.上海大学新型显示技术及应用集成教育部重点实验室,上海200444)

由颗粒物质组成的射流广泛存在于多种自然现象及工程过程之中,如喷墨打印、喷丸工艺、粉煤气化等.目前,在研究颗粒射流中逐步发展出多种产生颗粒射流的方法.Thoroddsen等[1]使用由直径为1.34 cm的高速大球撞击由直径为80 μm的玻璃小球堆积而成的基底,证明颗粒物质仍然可以在微尺度下通过基底的变形-反弹产生高密度的射流.通过高速气流载运颗粒也可以形成颗粒射流,在撞击壁面后得到类似液膜的流动结构.Shi等[2]利用这种方法发现了颗粒流液膜的厚度与来流的速度、颗粒大小无关,液膜的形态演化方式与来流直径和粒径之比有关.

近年来,对微电子机械系统(microelectronic mechanical system,MEMS)的研究不断增多.美国哈佛大学的研究人员就可以使用直径为100 nm的粉末颗粒,通过3D打印技术成功制造出局部精度可达1 μm的锂离子微电池[3]；麻省理工学院微系统技术实验室基于电喷印技术发展出一套低成本加工方法,该方法利用包含纳米颗粒的溶液制造出面积仅有0.03 mm2的微传感器,其内部电路的金属线仅10 μm宽,最小间隔50 μm[4],微纳尺度下的增材制造(additive manuafcturing)技术也因此得到高速发展；Fuller等[5]利用压电喷墨打印技术载运纳米颗粒成功构造出多种微电子元件,展示出喷墨打印技术在MEMS领域的巨大应用潜力；作为喷墨打印技术的一种替代选择,Huang等[6]利用气溶胶喷印技术成功地在室温下的A4纸质基底上完成了导电银质薄膜的低成本快速打印.

对于微纳米颗粒在射流中的输运,颗粒射流研究着眼于直径不小于1 μm的颗粒,流体环境影响往往可以忽略.而对于纳米颗粒,除喷墨打印和气溶胶喷印技术外,还存在多种应用方法.Xiao等[7]利用静电纺丝技术将纳米金属颗粒分散嵌入纤维材料中,减少了颗粒团聚的出现并提高了材料性能；花银群等[8]通过直流磁控溅射技术在单晶硅上制备铝纳米薄膜,并研究工艺参数对材料性能的影响,发现利用该技术制备的薄膜对特定的晶体结构颗粒有择优取向；余洁意等[9]利用热等离子法则成功制备出高纯度、高催化效率的SiC纳米颗粒.

由于纳米颗粒的射流在输运过程中往往需要各种液体、气体或其他物质作为载体,流体作用不可忽略,使得在实际应用中受到限制.本工作期望通过借鉴光镊技术的光场约束原理,构造出载体影响小或无需载体的微尺度颗粒射流.

光镊技术研究源于20世纪70年代,Ashkin[10]在实验室里偶然观察到激光对溶液中胶体颗粒存在扰动现象.之后,Ashkin与其合作者进行了利用激光进行原子/分子、颗粒捕捉的理论实验研究[11-12].直到1986年,Ashkin等[13]在实验室中第一次成功利用单光束梯度力阱实现了对从25 nm到10 μm范围胶体颗粒的稳定捕捉,才标志着光镊技术的正式诞生.光镊技术目前已被广泛应用于染色体分离、微粒间相互作用的测量等微小尺度研究工作[14-15].

现有的光镊技术文献大多集中于对单个微粒操控的研究,对大量颗粒的群体行为的影响研究罕见于文献专利之中.在研究有机发光二极管(organic light-emitting diode,OLED)真空蒸发镀膜技术时,受光镊光阱约束颗粒在光轴附近现象的启发,本工作尝试探讨利用光镊技术对颗粒流进行收束控制的可行性[16].对于球形微粒在电磁场中的受力计算方法,在Lorenz,Mie和Debye的工作中就已给出,即Lorenz-Mie理论,但该方法计算繁琐.在光镊技术诞生后,为了满足光镊设计的需求,先后发展出多种方法来简化计算过程.通常根据激光波长对颗粒半径的比值λ/a来区分应用于颗粒受力计算的方法.当λ/a＞20时,颗粒被称为Rayleigh粒子,可以使用电偶极子模型得到十分精确的结果[17]；而当λ/a＜1/5时,颗粒被称为Mie粒子,可以通过几何光学进行近似计算[10].更为通用的GLMT(generalized Lorenz-Mie theory)方法则可用于各种尺度的球形颗粒受力计算[18].

在先前的工作中通过理论分析与数值模拟的手段验证了Mie粒子的计算及收束效果[19-20],其结果适用于微米及纳米尺度的颗粒.本工作的重点在于纳米尺度Rayleigh粒子在激光作用下的行为.

1 物理模型与模拟方法

1.1 物理模型

本工作使用Lammps软件进行了数值模拟.Lammps(large-scale atomic/molecular massively parallel simulator)是美国Sandia国家实验室开发的分子动力学软件,可以对诸如原子、生物分子、颗粒流或其他粗粒化系统在不同力场与边界条件下的运动进行建模模拟.同时该软件架构内集成了消息传递接口(message passing interface,MPI)接口,简化了并行计算的实现过程[21].可以从其官方网站(http：//lammps.sandia.gov)获得该软件源代码,并根据需求进行修改.

最初的物理模型如图1(a)所示,该模型来自于真空蒸镀中常见的克努森盒-沉积衬板组合.令激光穿过颗粒流出孔,指向衬板或收集装置,在真空环境中诱导分子团簇或颗粒的运动.

在初步尝试从蒸发腔内一直模拟到外部的沉积衬板位置后,发现孔口前的流动模拟需要占用大量的计算资源.另外,虽然在模拟中孔口处克努森数(平均分子自由程与孔径之比)最小为0.003,已经处于粘滞流状态,但颗粒出流流量和速度分布形式仍然受孔长度、平均自由程、孔径等参数影响,其流动形态类似分子流,导致影响模拟结果的变量过多[22].由于最终关注的是激光对颗粒的收束效果,故综合以上考虑,问题可以进一步简化为孔口颗粒源与外部的激光作用域的组合,简化后模型如图1(b)所示.图中r为计数平面上一点距光轴的距离,ω0为激光的束腰半径,h为计数平面在z向的坐标,z0为激光束腰的z向坐标.

本工作将选择点源与面源来分别讨论激光对纳米颗粒流动的收束效果.

1.2 Rayleigh粒子所受激光作用力

根据Harada的工作,Rayleigh粒子受激光作用产生的散射力Fscat和梯度力Fgrad可以通过式(1)计算得到[17]：

式中：b z为z方向单位矢量,即激光传播方向；波数k=2π/λ,λ为激光波长；a为颗粒半径；m为颗粒对环境的相对折射率；n为颗粒所处环境介质的折射率；c为光速；I(x,y,z)为平均坡印廷矢量.

本工作选择了常见的线偏振基模高斯光束作为激光源,其平均坡印廷矢量在图1(b)中的坐标系中为

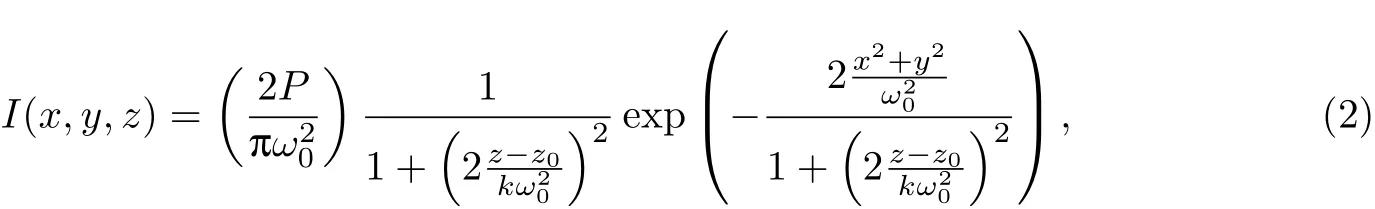
式中,P为激光器功率,ω0为激光的束腰半径.

1.3 模型的数值模拟

本工作中设置模拟区域大小为100 μm×100 μm×81 μm.不同的颗粒源放置在如图1(b)中的坐标原点处,向z轴正向发射颗粒.

对于模拟中的纳米颗粒,本工作均等效为理想球体,未引入其具体形貌的影响.纳米颗粒在近似真空的环境中运动,流体环境作用较小,运动过程中作用较大的主要是纳米颗粒相互之间与纳米颗粒-激光之间的作用.

本工作研究的是一个介观尺度问题,而这一尺度常用的粒子化研究方法有多粒子碰撞动力学(multiparticle collision dynamics,MPC)、耗散粒子动力学(dissipative particle dynamics,DPD)、直接蒙托卡罗(direct simulation Monte Carlo,DSMC)方法等[23].DPD方法经常被用来研究大分子在流体中的运动,通过对流体和分子进行粗粒化建模并应用统计方法得到的作用势,可以减少计算量,加速模拟过程.粗粒化的过程使得DPD方法的作用势中自然包含有反映流体环境的粘性作用及热运动的部分[24].MPC和DSMC方法与之类似,存在由流体环境引入的力项.这些方法通常针对的问题与本工作要模拟的目标差别较大.

参考文献[25]可知,纳米尺度均质球形颗粒之间的吸引力会在远小于其直径的表面间距内快速衰减,并且在极近距离与碰撞过程中其相互吸引力会由于颗粒的变形而难以计算,而排斥力整体表现为颗粒碰撞时的弹塑性变形.目前还没有找到适合本问题的颗粒吸引力的描述方法.根据Hamaker[26]的工作估算本工作中颗粒间的相互吸引力,在颗粒表面间距小于直径时吸引力才能接近激光作用力.对于纳米颗粒间的排斥作用,考虑到在颗粒流研究中,由于着眼于尺度大于1 μm的颗粒,颗粒间由范德华力产生的相互吸引作用可以忽略,故颗粒碰撞过程按照挤压变形进行计算,其中塑性变形、质量变化等影响通过碰撞耗散来体现[27].因此,本工作在模拟中使用了由Silbert和Brilliantov发展的颗粒流碰撞作用势来模拟纳米颗粒间的排斥作用[28-29],但未模拟纳米颗粒之间较弱的相互吸引力.本工作对于纳米颗粒间的相互作用的模拟并不完善,还需要进行进一步的研究讨论.

此时,按照颗粒流碰撞作用势(即式(3))计算球形颗粒i,j之间的相互作用：

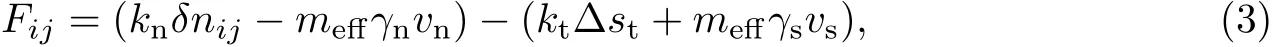
式中,kn为颗粒间的法向弹性系数(球心连线方向),δnij为颗粒中心距离的变化量,meff=mimj/(mi+mj)为颗粒碰撞时的有效质量,γn为法向阻尼系数,vn为2颗粒相对速度在法向上的分量,kt为切向弹性系数,Δst为2球的切向位移向量,γs切向阻尼系数,vs为相对速度的切向分量.这里,弹性系数和阻尼系数需要人工设置.由于本工作尚不考虑碰撞耗散及颗粒转动的影响,故在模拟中设置kt=0,kn=0.005 nN/μm,并关闭了阻尼系数的计算.

模拟时按照式(4)和(5),即Velocity-Verlet算法进行时间积分,得到颗粒运动轨迹[30]：

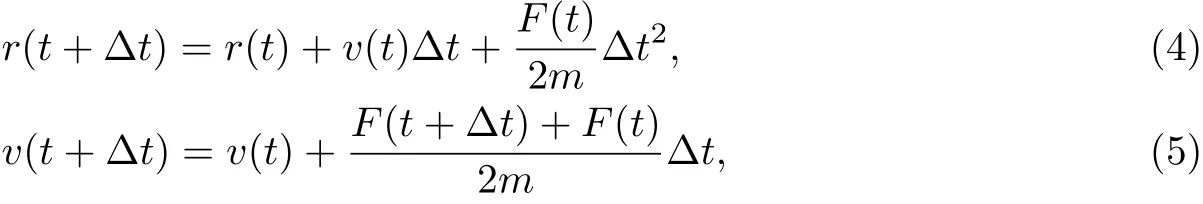
式中,r为颗粒位置矢量,v为颗粒速度矢量,F为颗粒受力,t为当前时刻,Δt为时间步长.

本工作选取了甘油这一常见的试验物质来作为数值模拟时颗粒的参数来源,同时沿用了真空蒸镀的环境假定.颗粒密度ρ=1.261×103kg/m3,相对折射率m=1.474 6,颗粒半径a取0.03 μm.环境折射率n=1(真空).

2 不同颗粒源模拟与结果

2.1 点源模拟

本工作首先使用点源模型开始研究,初步验证程序及激光收束颗粒的可行性.颗粒的初始速度需要满足一定的速度分布,为此本工作参考了真空蒸镀技术中对于各种蒸发源的叙述.通常在很多真空蒸镀过程中,除在蒸发源出口附近颗粒在飞行过程中几乎不发生碰撞[31].本工作选择了容易得到速度分布的点源作为研究起点.点颗粒源出发时的颗粒速度概率密度分布具有各向同性.基于这个特性和统计力学的基本原理,给出在颗粒平均初动能为常数的情况下,其速度矢量v的概率密度函数f(v)在极坐标速度空间上所满足的方程组(6),进一步推导得到由点源出发颗粒初始速率的概率密度分布(式(7)),由各向同性可以得到各速度分量满足的概率密度分布[32]：

当参考Oring的关于真空蒸镀沉积厚度的内容后,可以得到在如图1(b)所示的计数平面上,无激光收束时距光轴距离r处穿过平面的颗粒数密度满足的无量纲分布[31]：

式中,N为距光轴r处颗粒的穿越数密度,N0光轴处颗粒的穿越数密度.

30万个颗粒从坐标原点位置在0.42 s时间范围内随机注入计算区域,颗粒速度在进入模拟区域时按照速度分布式(8)赋予.虽然点颗粒源发射颗粒是全向的,但本工作仅模拟了如图1(b)所示的向上半球运动的颗粒.此外,模拟时需要设置发射距离间隔下限,以保证新注入颗粒不会在注入时刻就与已出发的颗粒发生碰撞,避免由于过近的距离导致碰撞计算时能量不守恒.为了减少模拟步数,允许时间步长Δt在模拟过程中,根据颗粒的最大速度与限定的单步最大移动距离在0.000 5 μs到0.050 0 μs区间上自动调整变化.

在模拟点颗粒源时激光器波长λ=632.8 nm,束腰位置z0=5 μm,束腰半径ω0=5 μm,模拟点颗粒源时的平均初动能取=0.038 8 eV.不同功率激光作用下在h=10 μm处得到的穿越密度分布如图2所示.

图2 不同功率激光作用下在h=10 μm处理论与模拟结果密度分布比较Fig.2 Comparisons of theoretical and simulation result density distributions under different laser powers at h=10 μm

由图2可以发现,随着激光功率增大,颗粒的分布向激光光轴(r=0)附近集中；而在无激光作用(P=0)时,图2(b)显示出模拟结果回归到如式(9)计算得出的无收束情况下应遵循的无量纲分布形式.因此,对于点源,激光确实可以在一定参数下有效地对颗粒在空间的运动轨迹进行收束,改善其在指定平面上的分布,同时模拟过程中少量碰撞后的颗粒运动未出现异常,初步验证了该程序可以正常模拟颗粒的碰撞与运动.

2.2 光聚纳米颗粒射流的理论分析和模拟

Lum[33]在1984年给出了的颗粒流的流体力学形式控制方程：

式中,ρ为局部的平均质量密度,T为颗粒温度,Q为颗粒流的热流矢量,P为颗粒流的压力张量,Γ为单位体积的能量耗散速率,F为单位质量所受体力.

颗粒流的温度T并不是指物质的热力学温度,而是指脉动速度的平均度量：

式中,f(v,r,t)为颗粒的速度分布函数,n(r,t)为颗粒的数密度,V(r,t)为速度场分布.

Lum构造的Q,P,Γ均为体积分数函数[33].(射流质量密度与颗粒密度之比)与颗粒温度的

在之前的工作中,通过体力项F,即式(12)引入了激光的作用：

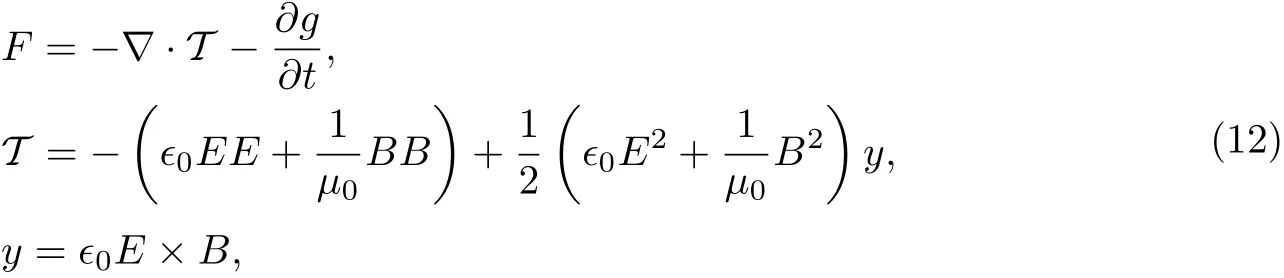
式中,T为电磁场的动量流密度,g为电磁场的动量密度[19].E,B分别为电场与磁场向量.y是一个单位张量.

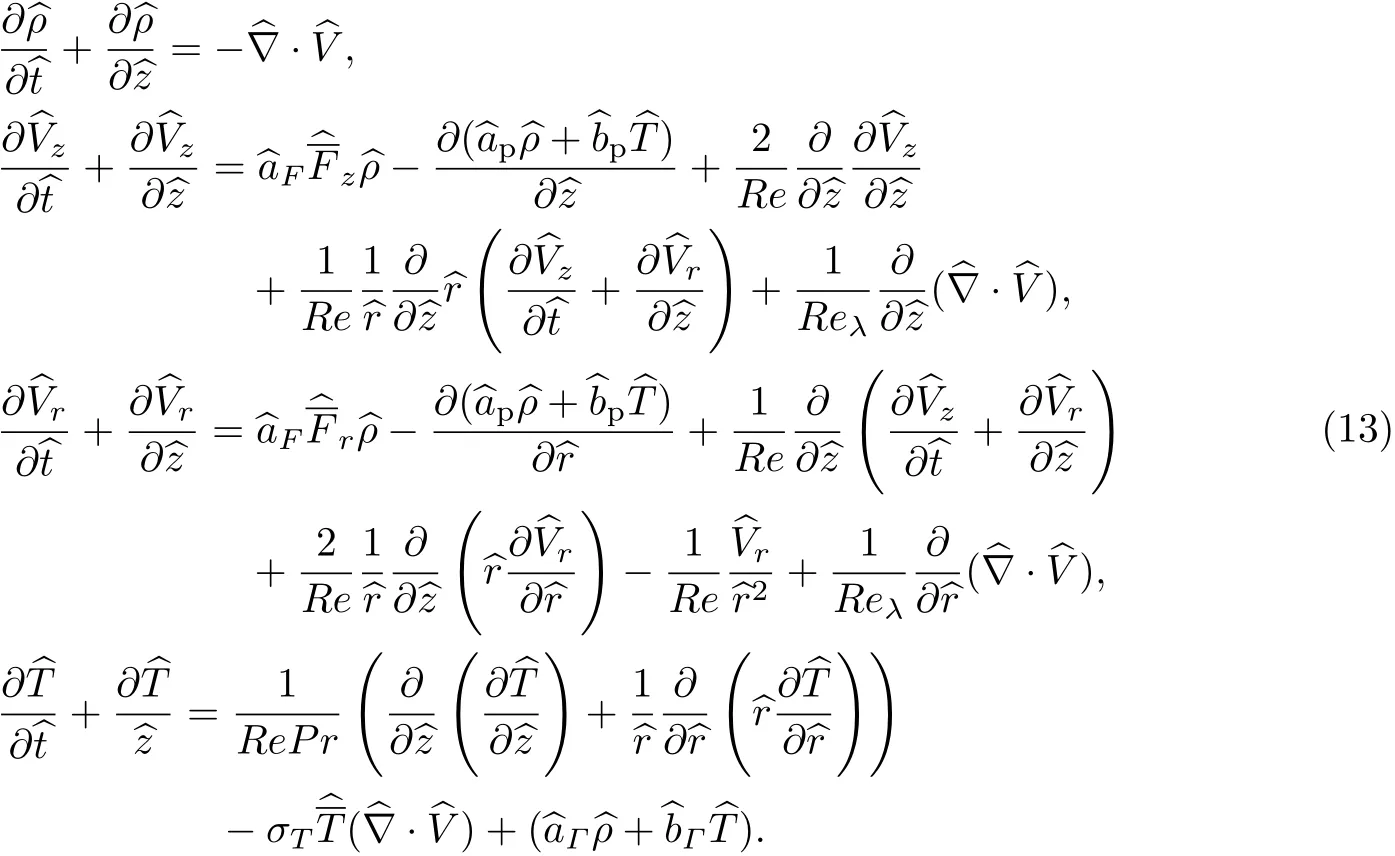
然后,构造了如下的颗粒流来进行数值分析.在真空环境下,颗粒射流由半径R0=3 mm的喷口以速率U=100 m/s流出.射流的出口体积分数为ν=0.1,最大体积分数νm=0.55.颗粒的直径为100 nm,密度为1.5 g/cm3,折射率为1.3.颗粒间相互作用接近于弹性碰撞,弹性恢复系数η=0.95.射流的颗粒温度为10 K.由于关注的是激光对颗粒射流的影响,引入无粘假设(Re,Reλ→∞)来简化后续分析[19].

参考文献[34],使用正则模态法将扰动变量ρ,(bVz),(bVr),bT写为如式(15)的形式[34],其中Ω为时间增长因子,k为轴向波数.当Ω＜0时流动稳定,Ω=0时流动中型稳定,Ω＞0时流动随时间增加会失稳：

代入方程组(13)中并利用无粘假定进行简化,得到一个2阶常微分方程：

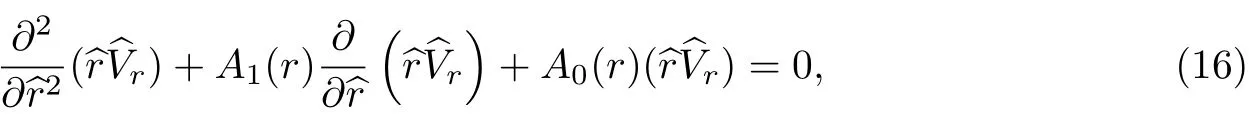
利用谱配置法对新方程(16)再次进行变换,成为如式(17)的线性方程组,以便数值求解.方程组为一齐次行列式,其存在非平凡解的条件是矩阵G(Ω,k,···)的行列式为0[19]：

利用Mu¨ller法对方程组(17)进行了求解[35].图3反映了计算得到的沿径向收束力和颗粒温度的变化趋势.图中径向力始终指向光轴,并随半径增大而增大,使得颗粒向光轴聚拢,射流存在收束的趋势.由黄凯[19]推导得到的的解析表达式还表明,如果激光功率增强,约束力就增大.而颗粒温度的分布则显示出颗粒在边界附近的活跃程度快速降低,内部的变化相对较小.图4是在不同电欧拉数Eu下,轴向波数k与增长因子Ωr的关系.电欧拉数Eu沿图中箭头方向减小,增长因子随之增大.由图中的情况变化可知,随电欧拉数Eu减小(如Eu≤0.01)后,增长因子Ωr＞0,按照正则模态法的分析系统将失稳,不能维持稳定射流；而当电欧拉数Eu≥0.5时,系统保持稳定.而增大电欧拉数Eu,最直接的方法就是提高激光功率,这与本工作利用激光可以稳定射流的构想基本一致.而图4还反映出激光对射流的长波与短波失稳的同时进行了抑制,这一点不同于常见的稳定性理论中典型表面力(即表面张力)对扰动波的选择性,通常表面张力对射流表面长波有失稳作用,对短波则有抑制作用[19].

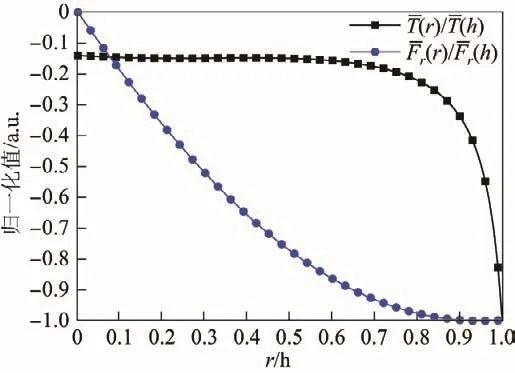
图3 归一化显示径向力与颗粒温度Fig.3 Reduced axial forceand granular temperature

图4 电欧拉数对流动稳定性的影响Fig.4 Electrical Euler number effects on the flow stability

2.3 纳米颗粒射流的颗粒动力学模拟

在实际科研生产过程中,颗粒源可能为喷管、坩埚等组件,有一定出口面积.对于宏观尺度下气体射流或射流中颗粒在喷管出口处的速度分布,虽然Anderson等[36]和Nathanson等[37]做过一定的理论与实验测量工作,但这些工作大多集中在喷管轴向上结合一维理论结果进行讨论,缺少更完整的理论描述.而在微纳尺度下对喷管进行模拟的过程中发现,几何参数的调整会引起出口流动速度分布发生复杂的变化.综合以上考虑,本工作通过在颗粒流进入模拟区域时叠加一个扰动速度分布的方法,来近似模拟发散的面源.在以下模拟结果中,扰动速度使用上述点颗粒源相同的概率密度分布函数.扰动速度分布参数设=0.004 eV,激光束腰位置z0调整为20 μm,其他参数与点颗粒源模拟相同.

为了减少模拟时的计算量,本工作参考了Moseler等[38]的颗粒注入方法.首先模拟了一群在直径为1 μm,长度为20 μm的圆柱管道内随机运动的30万个颗粒作为液柱,同时固定颗粒间相对位置.将液柱以固定速度vz=0.1 m/s注入,对进入模拟区域的颗粒解除相对位置的固定并在vz基础上叠加扰动速度.

图5为不同功率(P=0,0.5,1.0 W)激光收束下,颗粒流某一时刻空间分布的x方向投影.图中虚线为激光束的边界.从图中可以看到,颗粒的空间分布密度有明显变化,随着功率的增大向外散逸的颗粒密度逐渐降低,可见提高激光功率(电欧拉数)可以使系统形成稳定的射流,同时射流的直径在模拟区域中没有发生明显变化,即没有发生类似传统射流理论中的失稳现象.这与黄凯得到的激光会同时抑制长波与短波失稳的结论相一致.

图6为P=1.0 W时,50个相邻编号颗粒的飞行轨迹.本工作在模拟结束后通过计算颗粒的2个相邻时间步内飞行轨迹的角度改变量来判别是否发生碰撞.在如图5(c)所示的P=1.0 W的模拟中,以5°为判别依据时颗粒在模拟域中的平均碰撞次数为12.2次,10°时为5.66次,平均碰撞频率分别约为15.3×103Hz和7.08×103Hz(空气中分子碰撞的频率为109～1010Hz量级,即102量级速度与10-7量级分子自由程).从光束范围外飞出的颗粒占总颗粒数的2.36%.

图5 不同激光功率模拟下实时分布侧视图Fig.5 Run-time distribution side views from simulations with different laser powers

图6 P=1.0 W时50个颗粒的运动轨迹Fig.6 50 particale traces when P=1.0 W

在h=80 μm的平面上,统计不同功率下的累计分布密度(见图7),发现在本工作模拟的功率下光束范围内的颗粒分布区别不大.使用如式(18)定义的均方半径来表征整个平面上粒子位置的分散程度,以观察激光的收束效果(见图8).通过图中拟合的曲线可以看出,随着电欧拉数的线性增长,分散程度呈类似负指数下降的趋势,

图7 不同激光功率下h=80 μm处无量纲分布Fig.7 Reduced distributions with different laser powers at h=80 μm

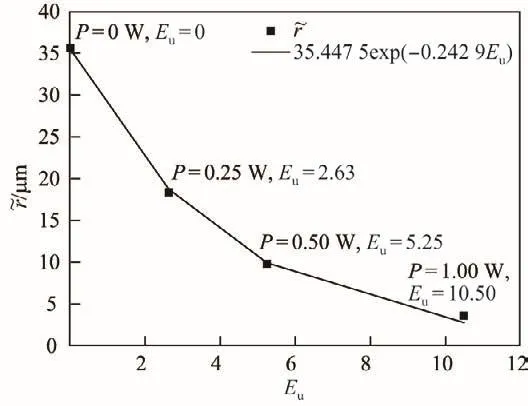
图8 不同Eu下在h=80 μm处的集中程度比较Fig.8 Concentration comparison with different Euat h=80 μm

3 结束语

本工作基于Lammps软件实现了由点源与射流产生的纳米颗粒流动叠加激光光场后的动力学模拟,同时应用理论分析的方法对激光作用下的纳米颗粒射流的稳定性进行了分析.点源模拟结果与经典真空蒸发沉积理论分布的比对后发现,激光功率P的增强可以提高颗粒分布的集中程度,初步证明激光是可以有效影响颗粒的运动轨迹,从而改善纳米尺度颗粒的沉积分布.

对于光聚纳米颗粒射流稳定性的理论分析表明,提高电欧拉数Eu可以提高颗粒射流的稳定性形成稳定射流,同时发现激光对于颗粒射流的长波与短波稳定性同时进行了抑制.而颗粒射流的模拟结果表明,通过增大激光功率P来提高电欧拉数Eu确实可以更加有效地约束颗粒形成射流,并且由均方半径随激光功率的增大而减小表明,颗粒的集中程度也随电欧拉数的提高而增强,表现出与理论预测一致的稳定性变化趋势.