文丘里型气动喷砂喷嘴冲蚀模拟分析
2019-10-31陈一鸣王卫强
王 博 徐 鑫 陈一鸣 董 美 王卫强
辽宁石油化工大学石油天然气工程学院, 辽宁 抚顺 113001
0 前言
集输管道表面经常会出现锈斑、污垢等现象,为解决这一现象,石化行业广泛采用涂层防护工艺,然而管道表面的粗糙度会直接影响防护工艺的质量[1]。因此,许多表面处理工艺应运而生,如化学试剂清洗、机械抛丸、磨料射流等[2]。同上述几种方法相比,气动喷砂具有抛光度高、粗糙度易控制、内孔清洁度达标等优点;同时,在相同条件下,气动喷砂装置使用成本远低于其他几种方式的使用成本。在气动喷砂系统中,喷嘴将气动流体的压力内能转化为速度动能,使砂粒在高速气流的携带作用下喷射到构件表面,达到表面清洗的目的。喷嘴结构的稳定性直接影响喷射的效率,但喷砂颗粒流经喷嘴会对自身内壁面造成严重的冲蚀磨损,降低装置的使用效率。目前对喷射器的研究主要集中在气动喷砂装置内流场分析及颗粒轨迹探索,如贾光政等人[3]运用CFD软件模拟了颗粒在收缩型喷嘴中的运动轨迹,计算了不同粒径流经喷嘴前后的动量变化量;王金东等人[4]运用欧拉-拉格朗日(Euler-Lagrange)法,对不同运行工况下的气固两相内流场进行了数值模拟,得到了气动流体的运动规律;李晶等人[5]利用试验优化方法,对304不锈钢在不同参数下的表面润湿性能进行了分析,并运用聚焦显微镜对结果进行了观察;王金东等人[6]通过改变喷嘴的直径对喷嘴内部气固两相流场进行了仿真模拟,得到了压力及速度的分布情况及颗粒撞击壁面的主要位置。针对气动喷射器自身冲蚀磨损的研究鲜有报道。因此,以文丘里型气动喷砂喷嘴为研究对象,运用CFD软件对喷嘴内流场分布及颗粒运动特性进行模拟分析,进而得到喷嘴的冲蚀规律及影响因素。
1 基本假设
1)设定喷射流体为理想流体,流体遵循绝热流动基本方程。
2)喷砂颗粒为球形,密度相同,表面光滑。
3)喷砂颗粒总体积分数小于喷射装置总体积的10%,可作为离散相处理。
4)只考虑连续相流体对离散相颗粒的阻力作用,忽略Saffman升力、Basset力及重力等影响。
2 数学模型
2.1 湍流模型
压缩气体为理想气体,喷嘴内流体的流动雷诺数大于2 300,流态为湍流,因此建立流动湍流模型。为使流动符合湍流的物理定律,对喷嘴壁面正应力进行某种数学约束。为保证这种约束的实现,需要将湍流黏度系数与应变率进行结合,所以选用Realizable k-ε模型[7]。该模型中,k和ε是两个基本的未知量,与之相对应的输运方程如下:
(1)
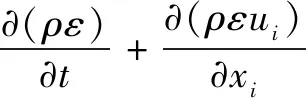
(2)
式中:ρ为流体密度,kg/m3;k为湍动能;xi、xj为空间坐标,m3;ui为i方向流体速度,m/s;v为流体运动黏度,m2/s;t为时间,s;u为流体流速,m/s;ε为湍动能耗散率;μ为流体动力黏度,Pa·s;μt为湍动黏度,Pa·s;Gk为平均速度产生的湍动动能;E为流体相流动应变率;σk、σε分别为k、ε对应的普朗特数,取值分别为σk=1.0,σε=1.2;C1、C2为经验常数,根据Launder B E等人[7]实验平台测得的实验数据,C1=1.44,C2=1.92。
2.2 离散相模型
对于气动喷砂两相流场,固体颗粒体积分数较小,可作为离散相处理,认为颗粒只受Stokes阻力的作用,忽略颗粒间的相互碰撞及剪切应力等所产生的影响[8-9]。根据牛顿第二定律,单位质量固体颗粒在气动阻力作用下的运动方程如下:
(3)
(4)
(5)
(6)
式中:FD为阻尼系数;up为颗粒流速,m/s;CD为曳力系数;Re为相对雷诺数;ρp为颗粒密度,kg/m3;dp为固体颗粒的粒径,mm;对于球形颗粒,在一定雷诺数范围内,a1、a2、a3为常数[10]。
2.3 冲蚀模型
采用Fluent中定义的冲蚀模型[11]对气动喷砂喷嘴进行模拟计算。冲蚀速率计算公式如下:
(7)
式中:Rerosion为冲蚀速率,kg/m2/s;Nparticle为颗粒数,个;mp为颗粒质量,kg;C(dp)为颗粒粒径函数,球形颗粒一般取1.8×10-9[12];v为颗粒相对流体速度,m/s;b(v)为相对速度函数,通常取2.6[13];Aface为壁面面积,m2;α为冲击角度,rad;f(α)为冲击角函数,采用分段线性函数进行拟合[14]。
(8)
2.4 流固耦合
气相采用Realizable k-ε湍流模型;固相采用拉格朗日(Lagrange)法进行轨迹跟踪。由基本假设可知,气体为连续相,喷射颗粒为离散相,相间耦合求解过程见图1。

图1 气固耦合流程示意图
3 计算域及网格划分
3.1 计算域
计算域为喷嘴内流场,考虑到流场的对称特性,取轴对称流场进行分析,计算域模型见图2。
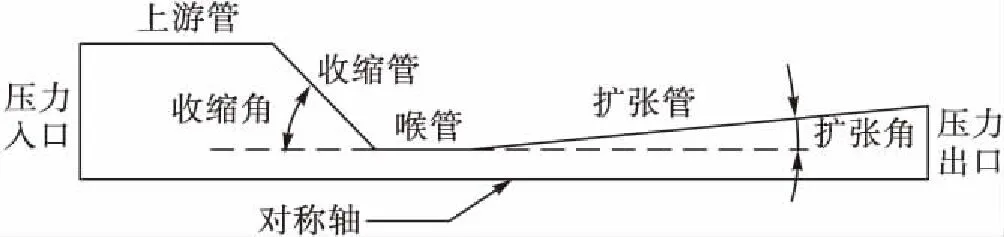
图2 计算域图
设定喷嘴入口为压力入口,壁面为无滑移标准壁面,喷嘴出口为压力出口;入口处离散相颗粒均匀分布,速度沿轴向方向,入口处及出口处设定Escape条件,壁面设置Reflect条件。
3.2 网格划分
由于文丘里型喷嘴几何结构较简单且规则,综合计算精度及计算成本,采用四边形结构网格对其进行网格划分,喷嘴内壁设置5层边界层,局部区域进行网格加密处理;通过对网格进行无关性检验,最终确定文丘里型喷嘴网格总数为35 335,具体网格划分见图3。

图3 网格划分图
4 仿真结果及分析
设定喷嘴入口管径φ1=40 mm,喉管管径φ2=5 mm,出口管径φ3=15 mm;入口段长L1=20 mm,收缩段长度L2=20 mm,喉管长度L3=10 mm,喷嘴总长度L=100 mm;渐扩角度为5.5°;入口总压为6.01×105Pa,出口压力为1.01×105Pa;流体为天然气,密度为0.667 9 kg/m3,颗粒材质为石英砂,密度为2 650 kg/m3[15]。
4.1 流场分析
选取收缩角为45°、扩张角为5.5°的工程常用文丘里型喷嘴进行流场分析,压力云图及速度云图见图4~5。

图4 压力云图
由图4可知,喷嘴入口段压力分布较均匀,收缩段出口至出口处压力变化较剧烈,喷嘴进出口压力比为1.007 5,其值低于等熵流动情况下的临界压力比1.89[16],因此,气流在喷嘴内完全膨胀,由于喷嘴出口段为渐扩型,使气流得到充分加速和膨胀,采用这种类型的喷嘴,有利于介质的加速,提高喷嘴的工作效率。

图5 速度云图
由图5可知,喷嘴入口段速度分布较均匀;收缩段速度变化梯度较大,且呈现层状分布;由于喉部管径急速缩小,使得喉管内速度骤增,取得速度最大值为83.8 m/s;出口段管径逐渐增加,从而使速度略微降低。
为直观地观察喷嘴内部压力及速度的变化规律,绘制喷嘴轴向压力及速度变化曲线,见图6~7。
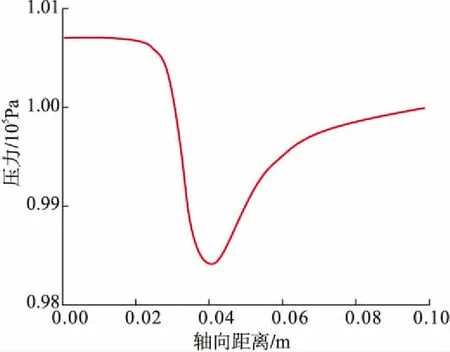
图6 轴线压力变化曲线图
由图6可知,喷嘴入口段至收缩段中部位置(0~0.025 m)压力值基本保持不变,近似稳定在1.007 5×105Pa;由于喷嘴收缩段管径逐渐减小,收缩段中部至收缩段出口附近(0.025~0.04 m)的压力迅速降低,由1.007 5×105Pa降至0.984 9×105Pa;因喉管处(0.04~0.05 m)管径急剧缩小,喷嘴内压力逐渐增加;由于喷嘴出口段管径逐渐缩小,喷嘴收缩段末端至喷嘴出口(0.05~0.1 m)压力仍呈现增加的趋势,根据喉管段与出口段压力变化的曲线斜率可知,喉管段压力增加的速度要远大于出口段压力增加的速度。
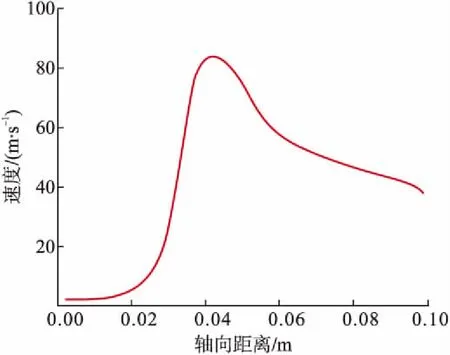
图7 轴向速度变化曲线图
由图7可知,喷嘴入口段(0~0.02 m)速度逐渐提高,但是提高的速度较缓慢,基本稳定在10 m/s;喷嘴收缩段(0.02~0.04 m)速度变化梯度较大,呈迅速提高的趋势,并且在收缩段出口处取得速度最大值,约为85 m/s;根据气体流动参数随喷嘴截面积变化的规律可知[17],喷嘴喉管段至出口处(0.04~0.1 m),速度逐渐降低,但喉管段速度降低的幅度要小于出口段速度降低的幅度。
4.2 冲蚀分析
固体颗粒对气动喷砂喷嘴壁面的冲蚀程度可用冲蚀率进行定义[18]。冲蚀率的本质为单位时间内固体颗粒对壁面金属材料的切削作用。由材料冲蚀的机理可知[19],固体颗粒在流体的带动下以很高的冲击速度撞击到材料表面,从而形成较为严重的冲蚀基坑,小直径颗粒由于质量较小会脱落到流场内,随流体继续向前流动,大直径颗粒由于质量较大的原因,部分颗粒会滞留在材料表面,削弱后续颗粒对材料的冲蚀作用。颗粒对材料的冲蚀过程示意图见图8。
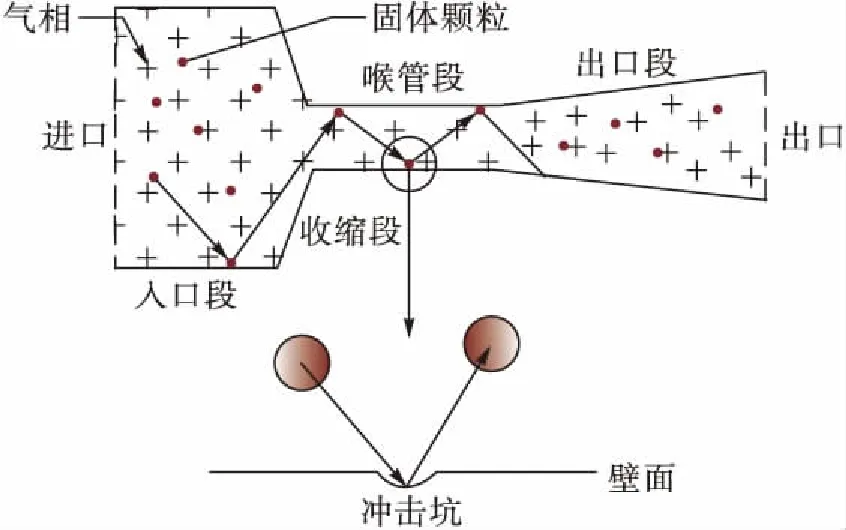
图8 颗粒冲蚀过程示意图
设定颗粒粒径为1 mm,颗粒质量流率为1×10-3kg/s,以收缩角度为45°的文丘里型喷嘴为例分析颗粒对壁面的冲蚀现象,冲蚀云图见图9。
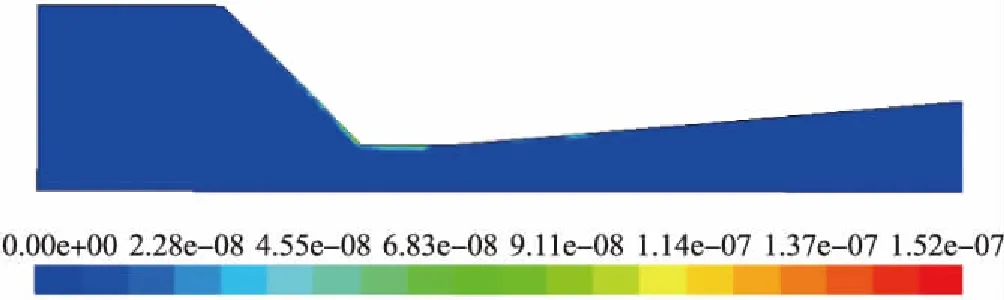
图9 冲蚀云图
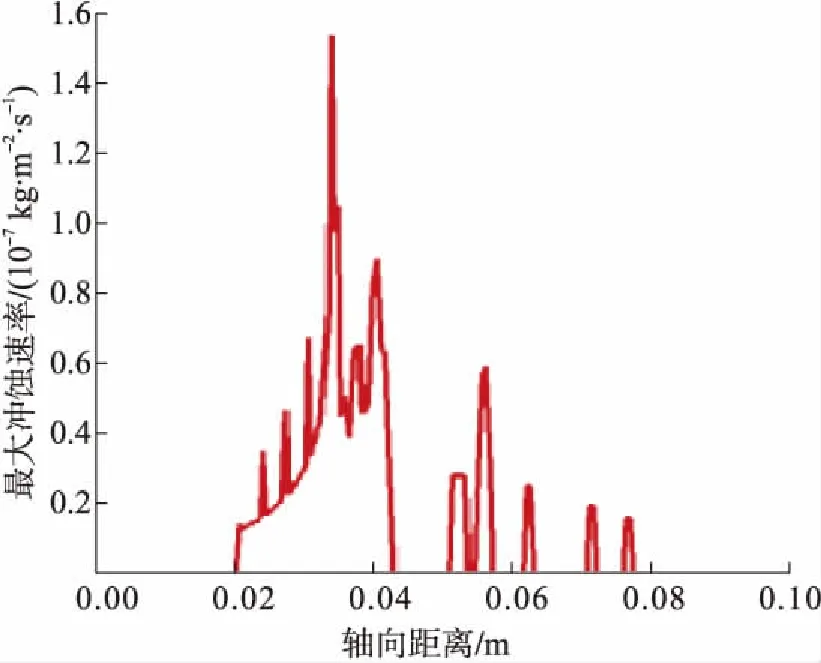
图10 最大冲蚀速率变化曲线图
由图9可知,文丘里型喷嘴的冲蚀区域主要集中在喉管位置,收缩管及扩张管也有轻微的冲蚀效果;喷嘴最大冲蚀速率为1.52×10-7kg/m2/s,位于收缩段与喉管段交界线处;喷嘴入口段与出口段冲蚀情况较小,可忽略不计。为直观了解喷嘴内壁面的冲蚀速率分布情况,绘制最大冲蚀速率波动曲线,见图10。
由图10可知,文丘里型喷嘴入口段壁面冲蚀速率接近于0;喷嘴收缩段内冲蚀速率逐渐增加,在收缩段与喉管段交界处(约0.035 m),冲蚀速率取得最大值;喉管内冲蚀速率有所降低,但降低的幅度较小;喉管段与出口段交界处,由于渐扩段管径逐渐扩大的原因,颗粒经壁面反射后越过该区域,因此在轴向0.045~0.055 m范围内,冲蚀速率再次降低至0;出口段内颗粒经壁面反复弹射后流出喷嘴,因此出口段壁面冲蚀出现往复波动的趋势。
4.3 收缩角对冲蚀的影响
由于0.01 mm的颗粒粒径太小,实际喷砂工程中很少使用[20],因此计算时保持喷嘴收缩段与出口段总长度恒定,通过改变收缩角度,对粒径为0.1~2 mm的颗粒在30°、45°、60°收缩角度条件下的颗粒运动特性进行仿真计算。基于材料冲蚀理论,对颗粒撞击壁面较严重的区域进行分析,从而得到冲蚀最严重的位置。颗粒沿入口径向均匀分布,运用Lagrange法对其运动轨迹进行追踪。
以粒径为0.1 mm的颗粒为例,不同收缩角度的颗粒运动轨迹图见图11。

a)α=30°

b)α=45°

c)α=60°图11 不同收缩角度的颗粒运动轨迹图
由图11可知,固体颗粒垂直于喷嘴入口端面射入流场,喷嘴入口段内颗粒分布较为均匀,且沿轴向平行流动,不同收缩角度的文丘里型喷嘴内部颗粒运动轨迹相似,但并不完全相同;相同参数设置的条件下,随着收缩角度的增加,喷嘴最大冲蚀速率逐渐加大;30°及45°收缩角度的喷嘴,颗粒运动轨迹较规则,并未出现颗粒“回弹”的现象,颗粒经收缩段加速后,反复撞击壁面后流出内流场,60°收缩角度的喷嘴,颗粒运动轨迹不太规则,由于收缩角度过于陡峭,因此部分颗粒经收缩段反弹后出现“回弹”现象;通过观察颗粒撞击壁面的位置可知,撞击点出现“滞后”现象。
4.4 颗粒粒径对冲蚀的影响
由冲蚀速率计算表达式可知,颗粒粒径的大小是影响喷嘴冲蚀的重要因素之一。颗粒粒径越小,自身惯性力就越小,因此其受连续相的气动阻力影响相对较大;随着颗粒粒径的增加,颗粒自身惯性力增加,从而使固体颗粒携带较大冲击能撞击收缩段壁面造成冲蚀磨损。以三种不同收缩角度的喷嘴为研究对象,颗粒粒径介于0.1~2 mm进行仿真分析。不同颗粒粒径的喷嘴最大冲蚀速率变化情况见图12。

图12 不同颗粒粒径的最大冲蚀速率变化规律图
由图12可知,气动喷砂喷嘴的最大冲蚀速率随颗粒粒径的增加呈现先减小再增加再减小最终趋于稳定的变化趋势。不同的收缩角度,其呈现的趋势大致相同,通过观察曲线的变动趋势可知,曲线先后出现3个拐点,产生该现象的原因是当颗粒粒径较小时,颗粒的质量较低,自身惯性力较小,受连续相流体的湍动作用较强,因此随着颗粒粒径的增加冲蚀速率呈减小的趋势;当颗粒粒径进一步增加,颗粒质量增大,颗粒随流体带动作用以很高的速度冲击到喷嘴壁面,因此冲蚀速率再次增大;当颗粒粒径增大至一定程度,颗粒的惯性力大于流体湍动力,部分颗粒在撞击壁面后会滞留在壁面,起到了一定的保护作用,减少了后续颗粒撞击壁面的次数,因此冲蚀速率再次呈现了降低的趋势;随着颗粒粒径的进一步增加,大直径颗粒滞留表面,后续颗粒持续流动,最终冲蚀速率基本保持恒定。收缩角为30°的喷嘴冲蚀情况最严重,60°喷嘴的冲蚀情况最不严重,45°喷嘴的冲蚀情况介于两者之间;不同收缩角度的喷嘴最大冲蚀速率变化规律近似相同,但随着收缩角度的增加,喷嘴最大冲蚀速率最小值存在“滞后”现象,即30°喷嘴的最大冲蚀速率在粒径为1.2 mm时取得最小值,45°喷嘴的最大冲蚀速率在粒径为1 mm时取得最小值,60°喷嘴的最大冲蚀速率在粒径为0.8 mm处取得最小值。
4.5 颗粒质量流率对冲蚀的影响
为研究颗粒质量流率对气动喷砂喷嘴冲蚀速率的影响,在相同的进出口边界的条件下,以粒径为0.1 mm的颗粒为例,设定颗粒质量流率介于1×10-3~1×10-2kg/s进行冲蚀分析。运用Fluid Flow软件进行仿真模拟,得到了不同颗粒质量流率对喷嘴壁面的最大冲蚀速率见图13。
由图13可知,不同收缩角度的喷嘴最大冲蚀速率随颗粒质量流率的增加逐渐提高;并且近似呈现线性关系;颗粒数量的增加,增大了颗粒撞击喷嘴内壁面的频率及概率,但与此同时颗粒间的相互碰撞造成的能量损失也随之增加,一定程度上减轻了固体颗粒对喷嘴内壁面的冲蚀,为了准确衡量最大冲蚀速率随颗粒质量流率的变动关系,运用数据分析软件进行曲线拟合,结果见图14。
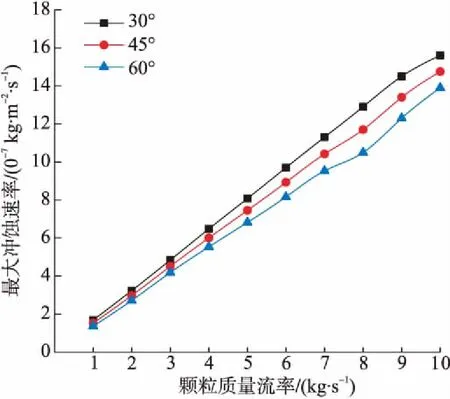
图13 不同质量流率的最大冲蚀速率图

图14 曲线拟合结果示意图
由图14可知,不同收缩角度的喷嘴最大冲蚀速率与颗粒质量流率之间线性拟合优度都大于90%,可认为喷嘴最大冲蚀速率与颗粒质量流率之间存在线性正相关关系;由拟合曲线斜率可知,随收缩角度的增加,喷嘴最大冲蚀速率增加的速度逐渐减慢,30°喷嘴的冲蚀速率变化最快,45°喷嘴的速蚀速率变化较慢,60°喷嘴的冲蚀速率变化最慢。
5 结论
基于流体力学理论,采用DPM模型,运用Fluid Flow软件对文丘里型气动喷砂喷嘴内壁面的冲蚀现象进行了仿真模拟,得到了以下几点结论:
1)文丘里型喷嘴的冲蚀区域主要集中在喉管,喷嘴收缩管及扩张管也有轻微的冲蚀磨损;以收缩角为45°、扩张角为5.5°的喷嘴为例,当进出口压差为5.0×105Pa时,最大冲蚀速率为1.52×10-7kg/m2/s,位于收缩段与喉管段交界处。
2)随着收缩角度的增加,喷嘴最大冲蚀速率逐渐增大;30°、45°收缩角度的喷嘴,颗粒并未出现颗粒“回弹”的现象,60°收缩角度的喷嘴,部分颗粒出现“回弹”现象;通过观察颗粒撞击壁面的位置可知,撞击点出现“滞后”现象。
3)喷嘴的最大冲蚀速率随颗粒粒径的增加呈现先减小再增加再减小最终趋于稳定;喷嘴最大冲蚀速率随颗粒质量流率的增加逐渐增大,并且近似呈现线性关系,线性拟合优度均大于90%。
