智能快递柜的动态定价研究

解亚宸，崔立新

（北京理工大学 管理经济学院，北京 100081）

1 引言

智能快递柜是一种新兴的快递交接模式，有着方便、快捷、高效、安全的特点，多在高校、居民区等人流密集、快递量大的场所投放使用[1]。智能快递柜有广阔的市场前景，但是由于收费方面存在问题，主流研发智能快递柜的公司尚都处于严重亏损阶段。为了解决这一问题，基于收益管理，建立了关于寄存以及取出快递的数学模型。

国内针对快递柜的研究主要集中于选址、系统设计、调研等，其中对“校园最后一公里配送”的研究较为广泛[2-5]。张晶蓉等通过系统分析、建立模型的方法研究了智能快递柜配送方式的成本核算，得出结论：智能快递柜公司只从派件赚取收入很难实现盈利，企业还需要寻找其余的增值业务[6]。罗江婷等通过文献调研以及归纳法，研究了智能快递柜在发展中存在的问题，为智能快递柜归结出四种盈利模式，同时提出智能快递柜若使用单一盈利模式很难实现利润增长[7]。

收益管理理论主要运用在航空、铁路以及公路领域。国外研究起步较早，目前收益管理理论已成为一个成熟的体系，应用领域广泛[8]。Shibata等通过数学建模的方法对短途铁路客流进行研究，建立了一个基于座位等级分布提高上座率的数学模型[9]。Gabriel等对动态定价政策实施和结果与收益管理的关系进行了研究，通过假设卖方面临的能力随机控制问题，设置产品数量及其相应的价格，以实现销售范围内的收入最大化[10]。Bertsimas 等通过改进捕获网络效应的确定性数学规划模型，解决了收益管理中需求不确定性、嵌套以及预订的动态问题，所提出的算法可以使得航空公司收益增加[11]。Gosavi 等基于票价等级、超额预订航班、不同票价等级的乘客的同时满足需求，以及航班随机取消的问题，建立一个SMART 算法优化模型。数值结果显示，该算法优于启发式算法[12]。国内针对收益管理理论的研究较晚，宋文波等以高铁市场收益最大化为目标，建立了不确定需求的动态定价与票额分配综合优化模型。算例分析表明该模型可以为高速铁路票额分配以及动态定价提供优化方法[13-14]。陈武华等采用数学模型算法，对酒店多房间类型的客房需求相关性的综合定价进行了研究，建立了动态规划模型，设计最优定价策略，最后得出结论，酒店多房间类型定价模型能够使得酒店收入增加[15]。

2 寄件的动态定价模型

2.1 问题描述及假设

快递柜每进行一次寄件服务时，都会向寄件人收取费用，该费用是智能快递柜企业的主要收入来源。针对现在的实际情况，快递柜收取寄件费用时，不论是在高需求还是低需求的市场环境下，只设置一个固定价格。这一定价举措会使得企业在高需求市场环境下，占用所用的资源后，得不到最大利润，在低需求市场环境下，无法形成价格优惠，吸引消费者使用快递柜寄件服务。

根据上述对快递柜的行业、市场分析，做如下假设：（1）市场上仅存在一家快递柜平台，不存在市场竞争的情况；（2）快递柜平台向寄件人收取服务费用基于快递柜数量剩余比为d；（3）单个快递柜存放一次快递的运营成本为c 元；（4）快递柜公司将面临两种不同的供需关系市场：供过于求—出现概率为fl，供不应求—出现概率为fh。

2.2 模型建立

当供过于求时，即未被占用的快递柜的数量大于需要快递柜平台服务的寄件人数量—供＞需，此时的需求函数为：

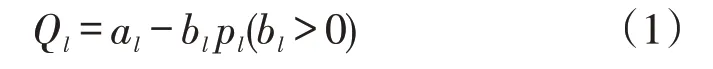
当供不应求时，即供＜需，此时的需求函数为：

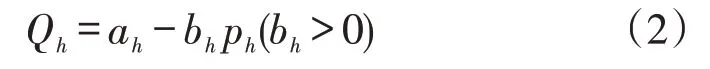
在低需求水平下，所有寄件人的需求能够得到满足，但是在高需求水平下，可能只有部分寄件人能够得到快递柜寄存快递的服务。因此当快递柜平台中的快递柜余量越多，快递柜平台的服务能力越高，寄件人得到的服务比率φ就越高。表1 给出本节所需的符号约定。

表1 寄件费用数学模型的符号约定

根据上述假设，目标函数即平台单个快递柜每天利润π为：

（1）采取固定价格策略。当采取固定价格策略时，服务价格不随需求波动而波动，即pl=ph=p1。此时平台利润函数为：

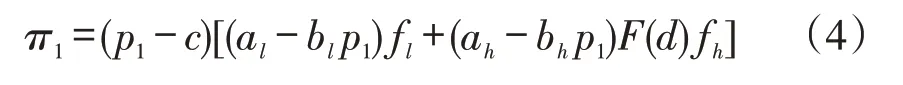
求取在无约束条件下，上述利润方程的最大值。

π1对p1求一阶导，得：

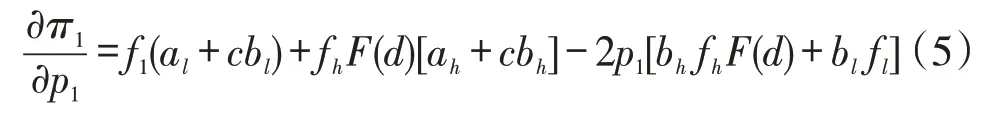
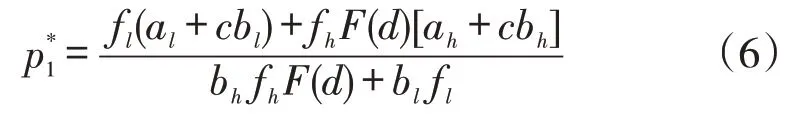
再π1对p1求二阶导，得：

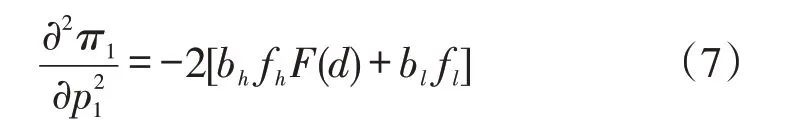
由于bh、bl、fh、fl均大于0，故，则最大值的一阶必要条件和二阶必要条件均满足，得出π1是p1的凹函数，且是极大值点，平台在该情况下的最大利润为π1()。

（2）采取动态定价价格策略。当快递柜平台采取动态定价策略，即pl≠ph。此时平台利润函数为：

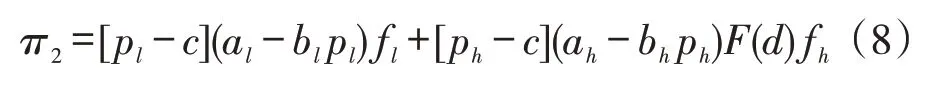
π2对ph求一阶导，得：

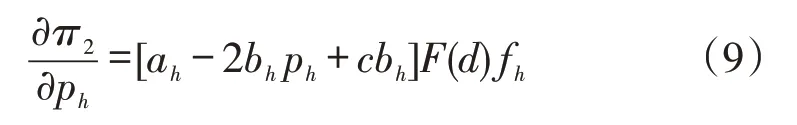
二阶导为：

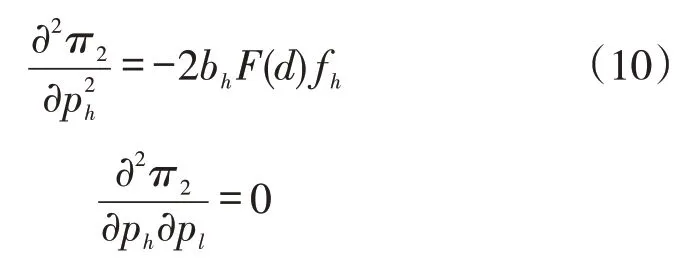
π2对pl求一阶导，得：

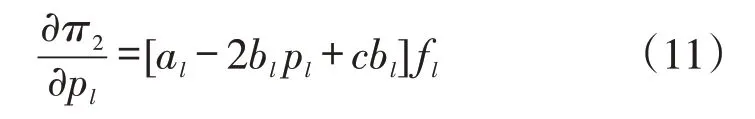
二阶导为：

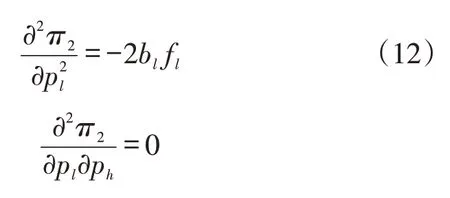
由于bh、bl、fh、fl均大于0，故那么π2关于pl、ph的Hessian矩阵：

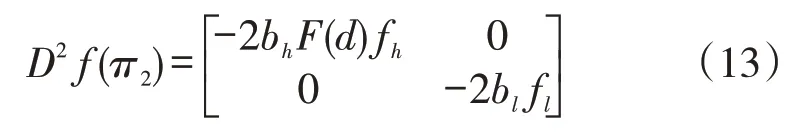
该矩阵为负定的，则该最值问题的一阶条件和二阶条件均满足。接下来求各种情况的最优价格：

根据以上得出π2是ph和的凹函数，且是极大值点，平台在该情况下的最大利润为

2.3 算例分析

将以上两种不同方案求解出的最优价格，代入到利润函数中求解对应情况下平台的最大利润。为了将固定价格和动态定价的不同效果直观展示出来，进行简单的算例分析。设定如下参数初始值（所有数值均根据网络搜索以及实际情况分析得来）：

生成的图像如图1所示。

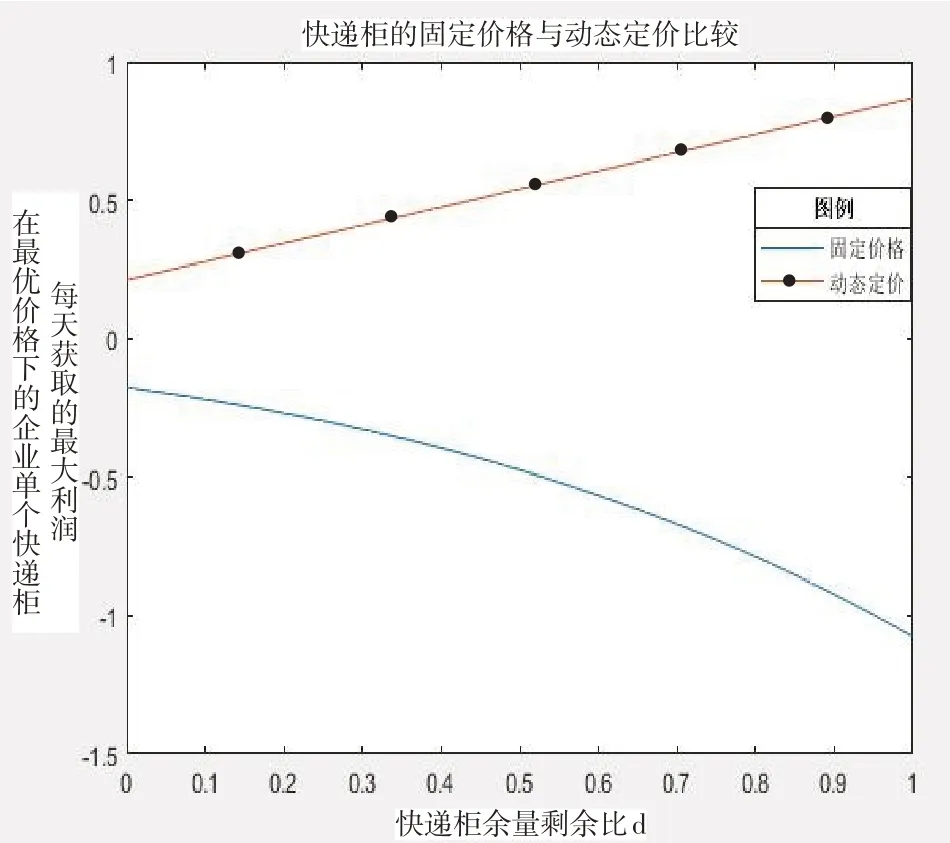
图1 快递柜固定价格与动态定价比较图

通过图1 的比较，说明现在的智能快递柜企业固定价格收取费用有很大的可能性使得企业处于长期亏损状态，这也符合现实生活中快递柜企业亏损的实际情况。而通过图1，可以看出若快递柜企业采取动态定价的定价策略会使得快递柜平台盈利。因此在当前社会背景以及技术支持下，快递柜企业采取动态定价策略可以实现收入增长，利润最大化。

3 取件的动态定价模型

3.1 问题描述及假设

快递柜不光在存放时进行收费，若是快递柜存放太久了，取件人未取走快递，造成快递柜占用时间过长，会使得平台利益受损，因此对于长时间未取走快递的取件人也应当加收超额费用。

目前针对超额费用征收的起征点一般快递柜企业设置在48h。超过48h，按1元/d收费。首先48h的期限设置导致快递柜平台收取超额费用的机会较少，同时又会占用快递柜，使得快递柜利用效率下降。其次，取件人对于1 元/d 的征收费用表示不满，消费者满意度下降，顾客忠诚度下降，那么就会导致顾客流失。因此，针对这一情况，建立关于收取快递存在时间超额费用的动态定价模型。

假设：（1）快递存放在快递柜中时间超过24h 开始收取超额费用；（2）对于超额费用定价的影响因素不考虑消费者心理、服务质量、快递柜的所在区域和人口密度等的影响，仅仅将价格视为快递柜余量D的函数；（3）每小时进行一次统计快递柜的余量，根据所统计出来的余量计算这一个小时应收取的超额费用。

3.2 模型建立

假定价格与快递柜余量的m次方成正比（m＜0）[14]。

ε是价格调整系数，D为快递柜余量，m为快递柜余量系数（与快递柜需求弹性有关），p为某一时间段的分段价格。

由于在存放时间中，快递柜余量为变量，为了方便计算，建立关于快递柜余量的递归方程。

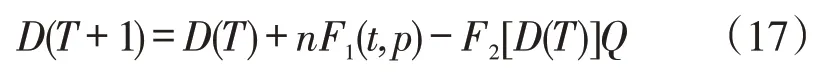
其中，T 为某个快递存放24h 后的某一时间段，T+1为某个快递存放24h后的下一个时间段，D(T)为存放快递24h 以后的某一时间段下的快递柜余量，D(T+1)为存放快递24h 以后下一时间段下的快递柜余量，Q为快递柜所处区域中每一个小时内有寄件需求的总人数，F2[D(T)]为当快递余量为D(T)时，寄件人会选择使用快递柜寄件的概率。F1(t,p)为某一时间段内，整个快递柜中所存放的快递会被取件人取走的平均概率。表达式如下：

其中n为当前占用快递柜总数，F1(ti,pi)为第i个快递柜中存放时间ti，价格为pi时，会被取件人取走的概率分布函数。

假设，在t ∈(0,+∞)内，快递一定会被取走，且存放时间越长，快递被取走的概率越大，因此基于以上假设，设F1(ti,pi)的概率分布密度f1(ti,pi)服从如下函数：

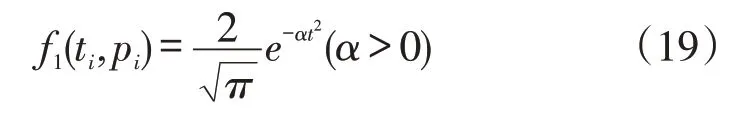
其中α为调整系数。可根据数学积分方法证明该函数符合以上假设。因此，对f1(ti,pi)进行不定积分，得：

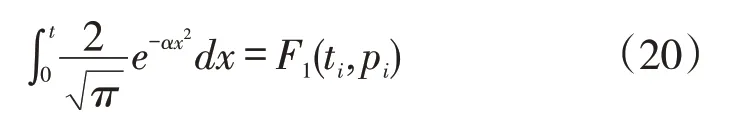
由于F2[D(T)]为概率，当D(T)＞0 时，其大小介于0和1之间，因此为了更好地描述实际情况，设：

其函数图像如图2所示。

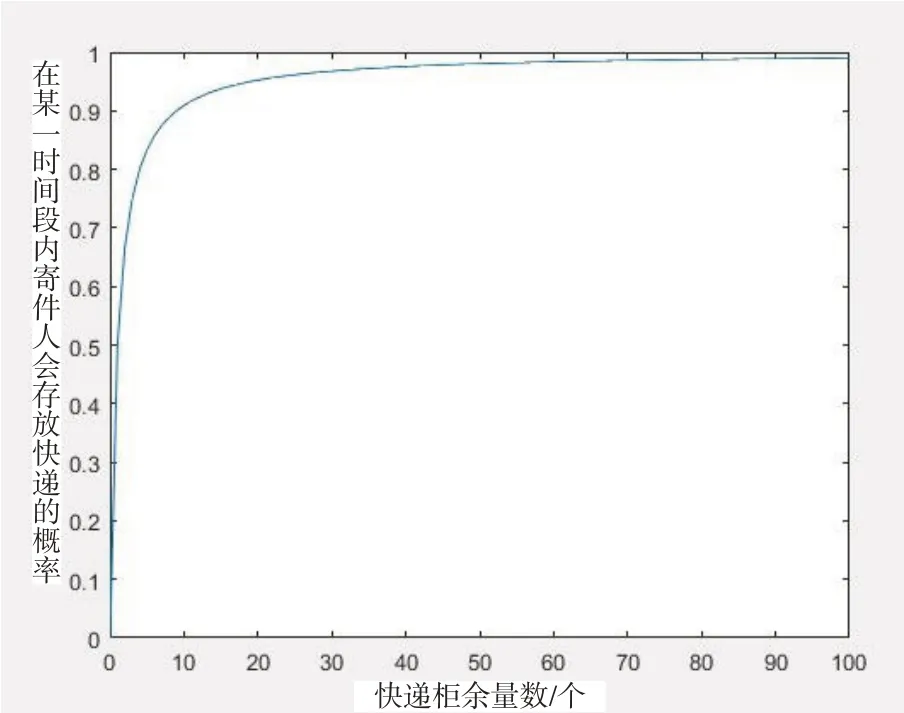
图2 F2[D(T)]的函数图像

根据F1(t,p) 、F2[D(T)]的公式，可将上述关于D(T)的递归方程改写成如下形式：

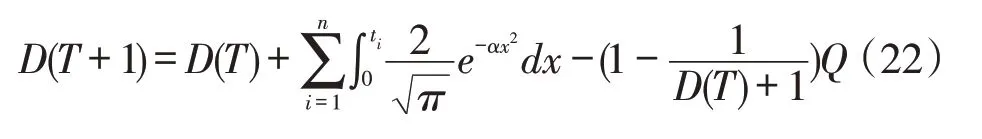
因此，单个快递取走时超过24h 额定期限后，所需要支付的超额费用P为：

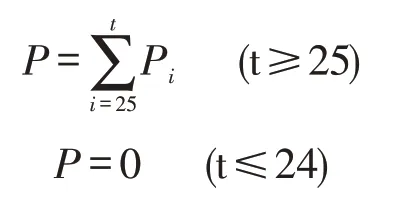
t 为快递存放时间，P 为单个快递需要支付的总超额费用。

3.3 算例分析

以丰巢智能快递柜公司为例，目前存放快递的超额收费标准为，在48h 内免费存放，超过48h 要加收1 元/24h（不足24h 按24h 计费）。若快递7d 不取，则快递会被公司平台退回原寄出地点。

根据该事例，选取α=0.000 4。则快递被取走的概率分布函数图像如图3所示。

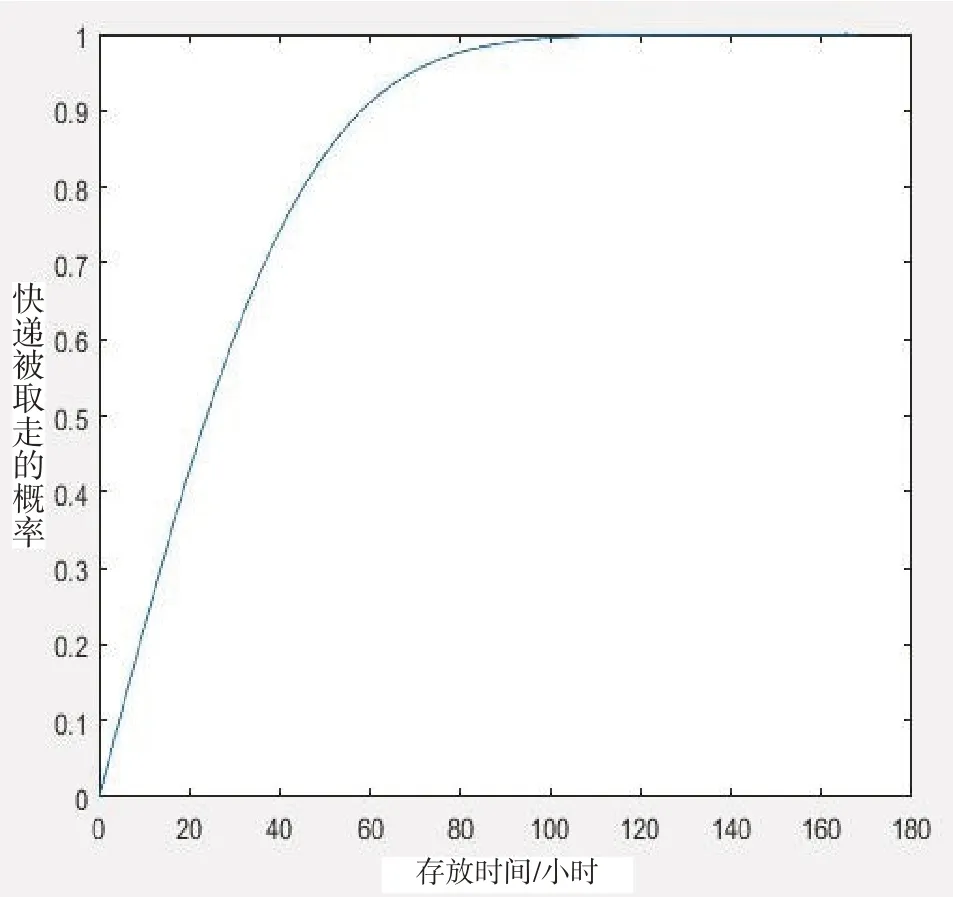
图3 快递被取走的概率分布函数F1(ti,pi)

假设在拥有100个快递柜的自提网点，某一快递在存放了49h 被取走，则一共有25 个时间段为收费时间段，运用MATLAB 产生25 次总数为100 个的随机数（随机数的产生按一定概率），计算每一次的平均取走概率，见表2。

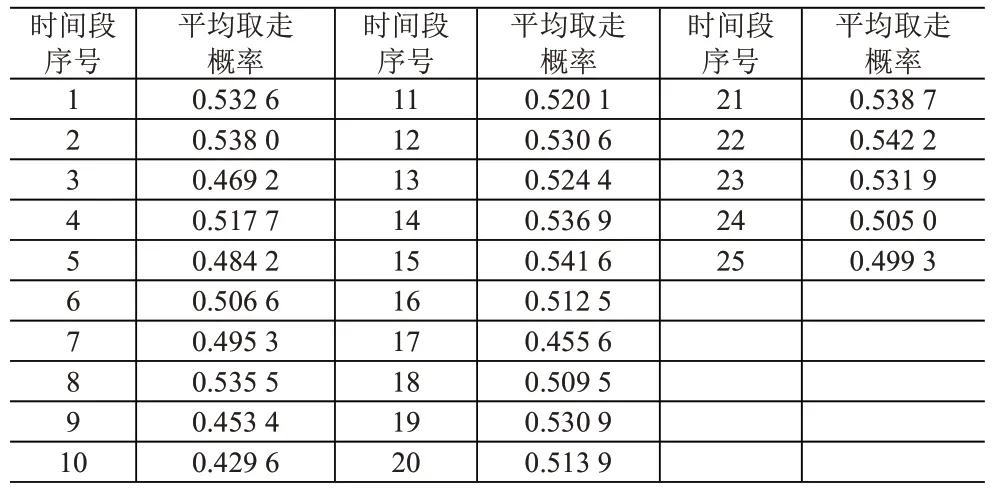
表2 每一时间段的平均取走概率

由于在不同时间段，来邮寄快递的人数是不同的，因此根据实际情况分别列举25 个时间段内的潜在寄件人数（Q），见表3。

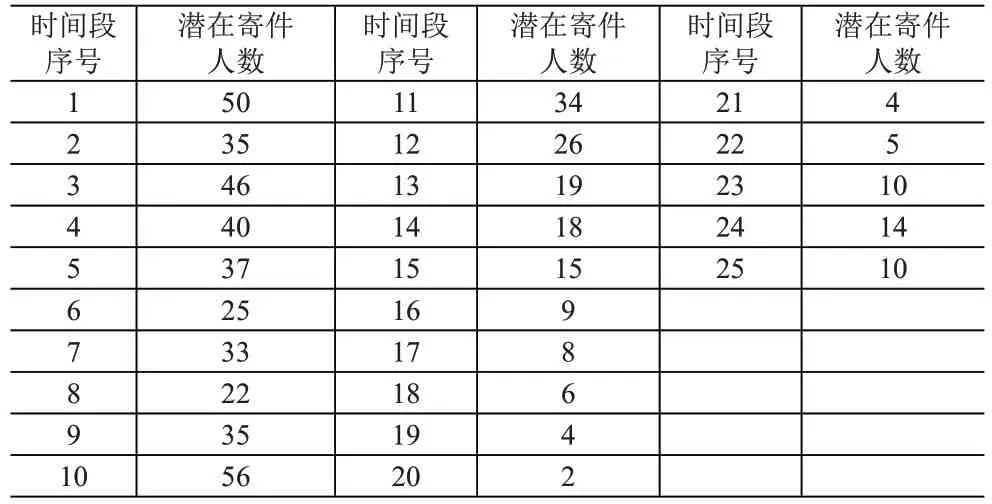
表3 每一时间段内的潜在寄件人数

设开始产生超额费用的时间段为第一时间段，且D(1)=14，可用的快递柜总数为100 个，通过MATLAB 进行递归方程运算，得到其余24 个时刻的快递柜余量，见表4。

表4 每一时间段内的快递柜余量

时间段价格公式p=εDm，ε是与需求有关的变量，同时由于没有确切的快递柜需求预测数据，因此假设ε=250，选取特定m值，将每个时间段的快递柜余量(D)进行取整处理，将不同m 值带入时间段价格公式，得出在不同m 值情况下的，每一时间段的价格。再通过进行加和，得到单个快递所收取的超额费用，见表5。

表5 不同m取值下的总超额费用

通过表5 可以看出，当m=-2.8 时，通过动态定价所收取的超额费用与实际收取的费用相同，其散点图如图4 所示。在ε=250 时，只要选取m 值大于-2.8，即可超出实际收取费用，使得公司利润增加。

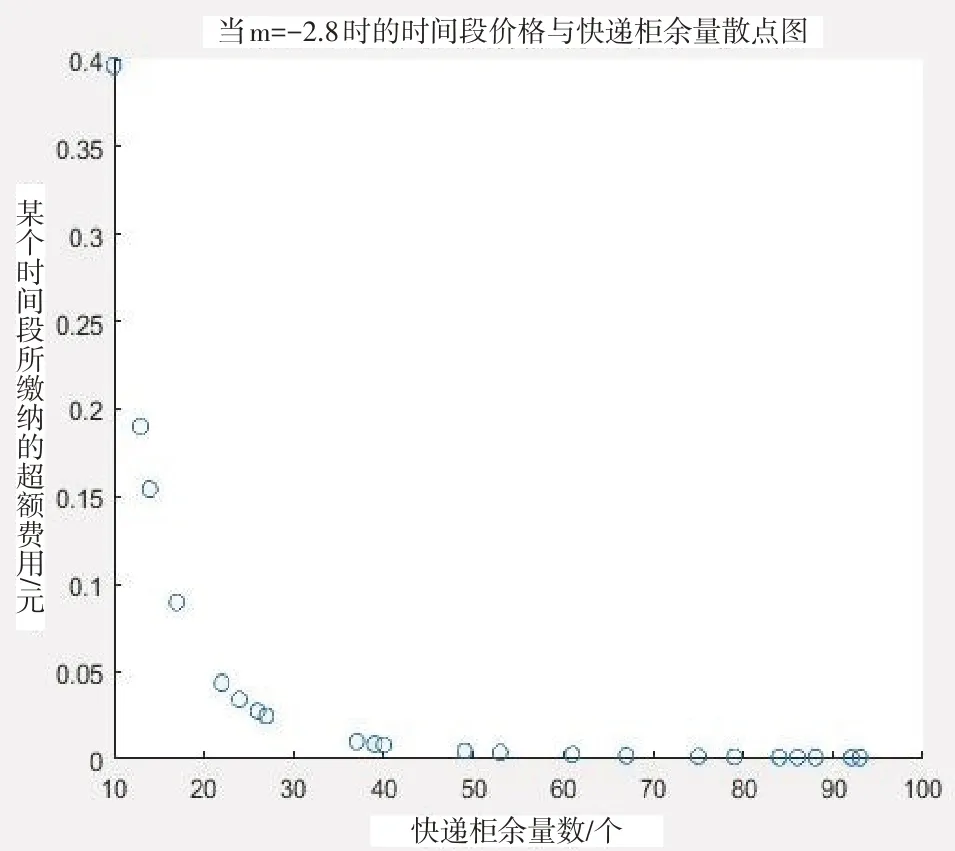
图4 m=-2.8的时间段价格与快递柜余量散点图

当然一味地增加m 值，虽然单个快递的收取的超额费用增加，可增加快递柜企业利润。但是随着价格的增加，需求就会下降，因此企业需要合理预测m值。

4 总结

随着我国电子商务的发展，快递行业迎来了迅速的发展，同时也面临着很大的挑战。末端配送成为快递行业一大痛点。智能快递柜的出现虽然解决了一部分问题，但是其经济效益低下又成为了亟待解决的问题。

本文以智能快递柜为研究对象，运用数学建模的分析方法以及收益管理理论知识，对智能快递柜动态定价进行优化研究。确定了智能快递柜的双向定价机制，最后建立了在低需求与高需求情况下的智能快递柜的寄件动态定价模型，并用案例分析证明模型的有效性。动态定价为平台带来的利润大于固定价格，因此该数学模型有现实意义，对智能快递柜企业有一定借鉴作用。最后建立了基于快递柜余量的时间段分段价格函数，根据不同调整系数，找到单个快递的最大超额费用值。