基于BP神经网络的物流网点规划设计

席钌姿，刘 昊，王 鑫，张 磊，武薏敏，刘 秦

（1.湖南工学院 安全与环境工程学院，湖南 衡阳 421002；2.湖南工学院 计算机与信息科学学院，湖南 衡阳 421002；3.湖南工学院 经济与管理学院，湖南 衡阳 421002）

1 引言

如今市场各种类型的物流公司都在不断扩大其服务的辐射范围，力图实现物流网点的最大辐射范围和最佳利用率。物流企业的物流中心选址决策在其公司的项目计划中与物流企业的营业利润和企业的稳定发展有着直接的联系，物流网点在整个快递企业物流系统中起着承上启下的关键作用，是货物邮件接收地与发送地之间连接的中间桥梁。正确的物流中心选址是能否成功建立快递系统过程中决定性的一步。所以对物流网点选址方法的研究和选用是确定物流网点经营成功与否的决定性因素之一。

一些现有的快递企业在进行物流中心位置选择时并没有仔细地考虑各种影响因素，而是大致地选择了某个特定的区域来进行建设，这样的物流中心将会在以后的长期运营中逐渐出现因其选择位置决策错误所带来的隐患，其对于正处在快速发展下的快递企业来说极其不利。选址决策是实现物流系统高效运营最重要、最困难的决策，属于长期的战略决策。同时设施选址是一个十分古老而又经典的问题，古代的选址决策往往以经验、制度甚至迷信思想为依据，缺乏科学性。1909 年德国学者韦伯第一篇选址论文的发表标志着设施选址问题进入到科学研究时代，Hakimi 于1964 年发表的关于网络多设施选址的论文是设施选址问题发展为一个系统、科学理论的里程碑。此后，设施选址问题被引入一个更宽广的领域,包括生产中心选址（Eilon,etal,1971）、交通枢纽选址（Wirasinghe & Waters,1984）、变电站选址（Hochbaum,1982）等，选址理论研究进入繁荣时期。进入20 世纪80 年代以后，现代物流理念的产生，则使得设施选址理论的研究内容更加丰富。

为了解决由多个因素组合而成的物流网点选址问题，提高物流网点选址的战略性，本文提出了基于BP神经网络的物流网点选址方法。对已有物流网点进行分析，建立三层BP 神经网络，利用该BP 神经网络对湖南省各个市的决策指标数据进行处理，得到最佳的物流网点选址方案。

2 基于BP 神经网络的物流网点选址设计

本文以湖南省某物流公司为例探讨基于BP 神经网络的物流网点规划设计，该公司主营公路零担货物运输，目前在湖南省已建立网点38 个，计划在2018 年12 月实现市区网点30 家；2019 年12 月实现新增市区网点10家；2020年12月实现新增市区网点10家，达到可以覆盖各市区的网络。

2.1 物流网点选址的影响因素

实际选址面临复杂环境，物流网点的功能和服务特性决定了物流网点布局的城市边缘、交通条件以及网点用地等。总的来看，零担货物配送网点的选址需要考虑客户分布、经济环境、经营环境因素、交通条件因素、其他因素五大因素。根据这五个一级指标选取了21个二级指标，具体见表1。

表1 影响选址指标

2.2 建立网点选址模型

2.2.1 确定网点选址决策的指标体系。由于在确定影响物流网点选址因素时，所选取的指标往往存在相互影响的关系，收集到的数据存在单位不统一的问题，难以统一处理，因此对原始数据进行隶属度处理建立模糊评价矩阵，再对模糊评价矩阵进行主成分分析，对前文所选出的21 个影响因素进行处理之后得出5个影响最大的组合主成分，从而构成网点选址决策的5个指标体系。

（1）建立模糊评价矩阵。搜集已有的正在运营的网点和预选方案的5个一级指标及其21个二级指标的详细历史数据资料，对长沙市、株洲市、湘潭市、衡阳市、邵阳市、岳阳市、常德市、张家界市、益阳市、郴州市、永州市、怀化市、娄底市、湘西自治州的数据，经过隶属度处理得到模糊评价矩阵，结果见表2。

（2）进行主成分分析。对模糊评价矩阵进行主成分分析，21个指标标准化后的初始特征值、累计贡献率以及各个指标在每个主成分的权重见表3、表4。

由表3 可以看出，前5 个主成分可代表原指标93.289%的信息量，所以可用前5个主成分作为BP神经网络的输入。由表4 可以得出每个指标在主成分所占权重，从而计算出长沙市、娄底市、邵阳市、常德市、岳阳市、株洲市、湘潭市、郴州市、张家界市、衡阳市、怀化市、永州市、湘西市、益阳市在五个主成分的得分，具体见表5。

表2 地州市模糊评价矩阵

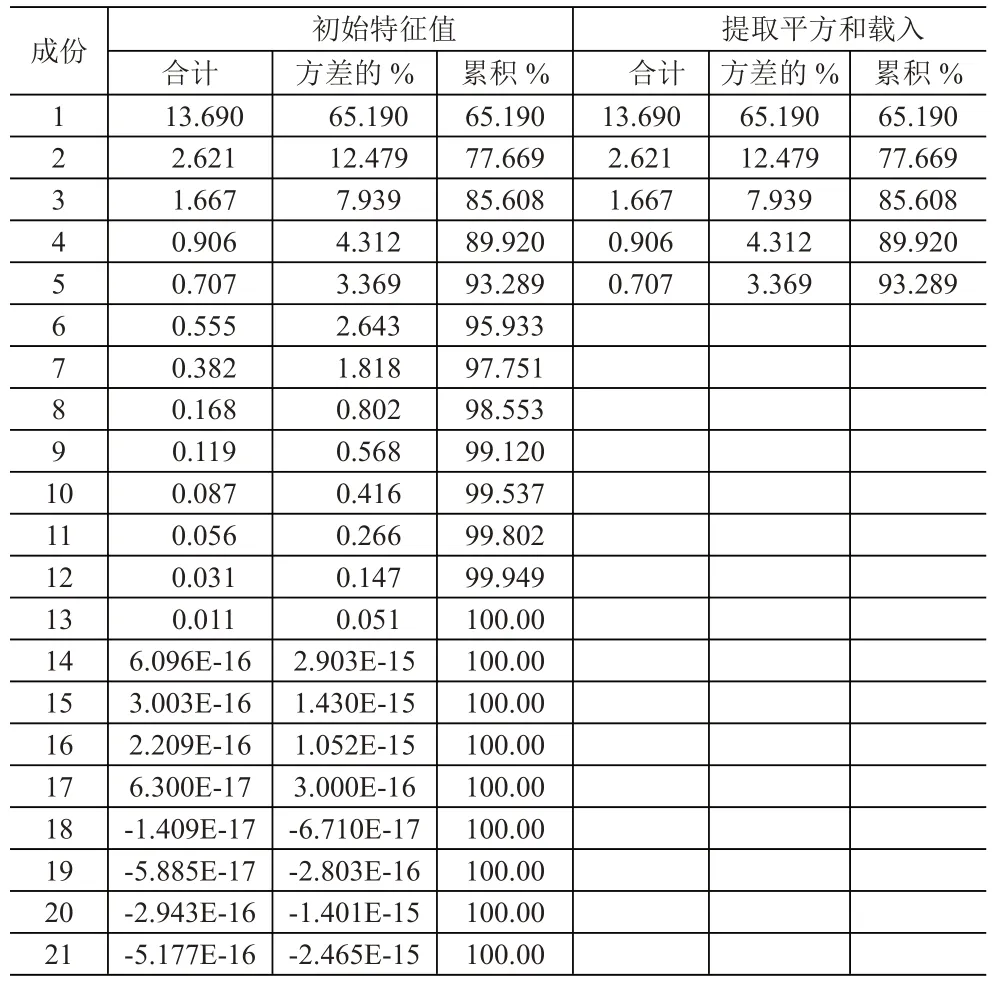
表3 地州市主成分分析总方差解释

2.2.2 设计BP神经网络模型

（1）确定网络节点。根据上述分析得知一共有5个主成分，所以选择5 个输入，即输入层有5 个节点xi(i=1,2,...,5)分别表示每一个样本的5个主成分；经过分析隐含层设置为4 个节点。最终要得到各个城市的评价值，所以输出层只需要1个节点。

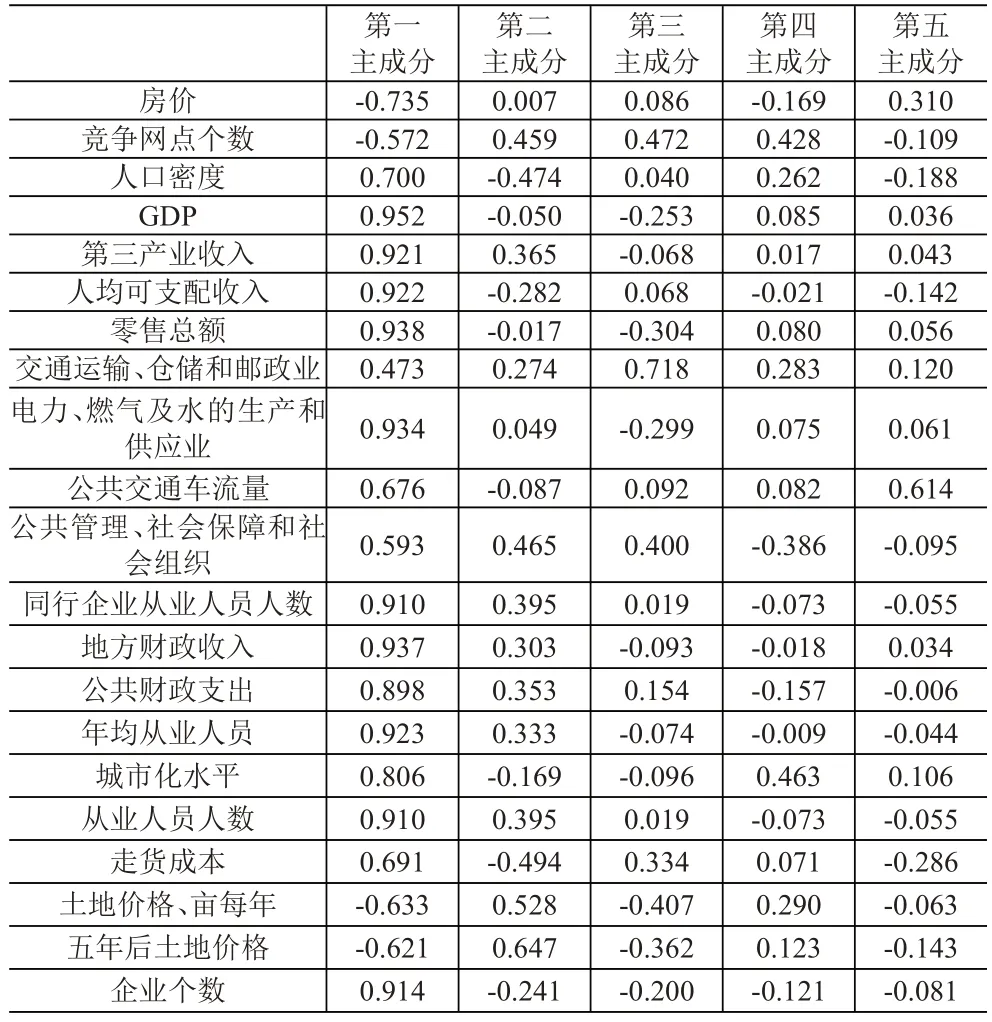
表4 地州市主成分分析成分矩阵

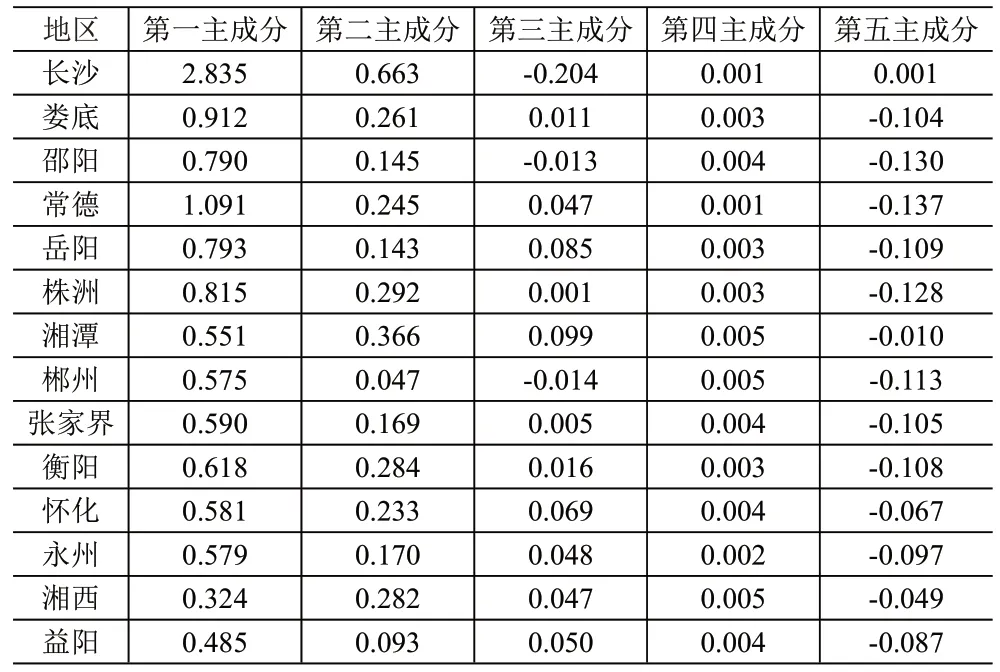
表5 地州市主成分分析得分

（2）建立传递函数。传递函数是BP 网络的重要组成部分，必须是连续可微的，BP网络常采用S型的对数或正切函数和线性函数。在这里取输入层到隐含层的传递函数为tansig；隐含层到输出层的传递函数为logsig；训练函数为Trainlm。

（3）确定训练速率。网络训练的速率是非常重要的问题，如果太大会使结果十分震荡，但是如果太小模型很难收敛到一个点上。所以，在网络设计中可以用不同的速率进行运算，然后在这些情况中选择一个最好的训练速率，其一般取值在(0.01，0.6)之间。在这里取值为0.3。

（4）迭代次数。需要设置一个最大的迭代次数，如果长时间不能收敛，得到相应的结果就得设置一个最多迭代的次数，如达到这个次数还没有收敛出结果，就自动终止运行。本文把最大迭代次数设置为1 000次。

综上得到各个参数及取值见表6。

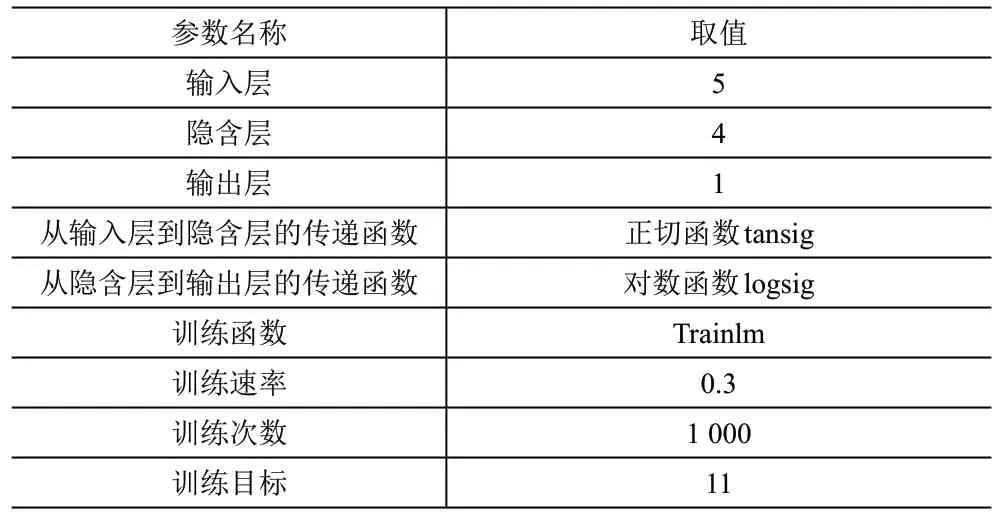
表6 BP神经网络模型各种参数训练表

2.2.3 训练神经网络

（1）建立选址目标的训练网络。将主成分分析后的新指标作为BP 神经网络的输入，并在MATLAB上运算程序得到一个逆向的学习模型和最优连接权值。

训练代码如下：

clear

p=[2.835 345 984 0.663 264 597 -0.203 929 14

0.000 756 11 0.000 906 214 ;

0.912 126 741 0.261 053 62 0.010 984 141 0.002 949 431 -0.104 106 081;

0.789 706 613 0.144 855 771 -0.013 161 939 0.003 665 237 -0.130 283 917];

t=[1 0.79 0.74];

p_fore=[1.091 384 917 0.245 207 383 0.047 018 996 0.001 484 083 -0.137 434 03;

0.793 239 038 0.142 809 86 0.084 913 331 0.002 855 883 -0.108 933 877;

0.814 993 113 0.292 465 007 0.000 692 087 0.002 611 506 -0.127 976 822;

0.550 958 1 0.366 217 291 0.098 668 241 0.004 969 056 -0.010 155 744;

0.574 634 199 0.046 959 401 -0.014 469 694 0.005 013 778 -0.112 517 673;

0.590 366 7570.169 374 5540.004 805 233 0.003 971 782 -0.105 186 761;

0.617 834 911 0.283 746 295 0.016 470 456 0.003 078 037 -0.107 884 651;

0.580 637 0270.233 245 823 0.068 935 204 0.004 120 578 -0.067 414 393;

0.579 217 21 0.170 064 205 0.047 830 268 0.002 363 84 -0.096 747 32;

0.324 152 7690.281 946 952 0.047 368 062 0.005 405 754-0.048 955 169;

0.484 672 787 0.093 459 083 0.049 787 872 0.003 890 07 -0.086 697 753;

];

net = newff(minmax(p')，[4，1]，{'tansig'，'logsig'}，'train

lm')

net.trainParam.epochs=1 000;

net.trainParam.lr=0.3

net = train(net，p'，t)

y = sim(net，p')

error = y-t

训练结果如下：

y=

1.000 00.790 00.740 0

error=

1.0 e-006*

-0.431 9 -0.000 6 -0.000 5

y和error表示实际输出和误差，可以看到误差已经是10 的负6 次方的量级了，已经达到了要求。故训练得到的网络可以用来对预选网点进行处理。

p[1]表示矩阵的第一行也就是第一个样本长沙市的数据，共有5 个数据，其中每一个数据就是一个主成分，也就对应了每一个输入。

p[2]表示矩阵的第二行第二个样本娄底市的数据，共有5个数据，其中每一个数据就是一个主成分，也就对应了每一个输入。

p[3]表示矩阵的第三行第三个样本邵阳市的数据，共有5个数据，其中每一个数据就是一个主成分，也就对应了每一个输入。

其中t 矩阵中的1 表示对长沙市的打分，0.79 表示对岳阳市的打分，0.74 表示对娄底市的打分。t 矩阵也就是网络的期望输出值。

‘tansig’表示输入层到隐含层的传递函数。

‘logsig’表示从隐含层到输出层的传递函数。

‘trainlm’表示训练函数。

net.trainParam.epochs=1 000 表示训练的次数为1 000 次，当训练了1 000 以后，网络就会停止学习输出结果。

net.trainParam.lr=0.3表示训练的速率为0.3。

y表示按照net完成训练以后的实际输出值。

error 表示实际输出值减去期望输出值，也就是误差。

2.2.4 用经过训练的网络对预选网点数据进行处理。训练代码如下：

训练结果如下：

图1 是1 000 次训练时误差的变化曲线图，可以看到在经过1 000次的训练以后，网络已经稳定。

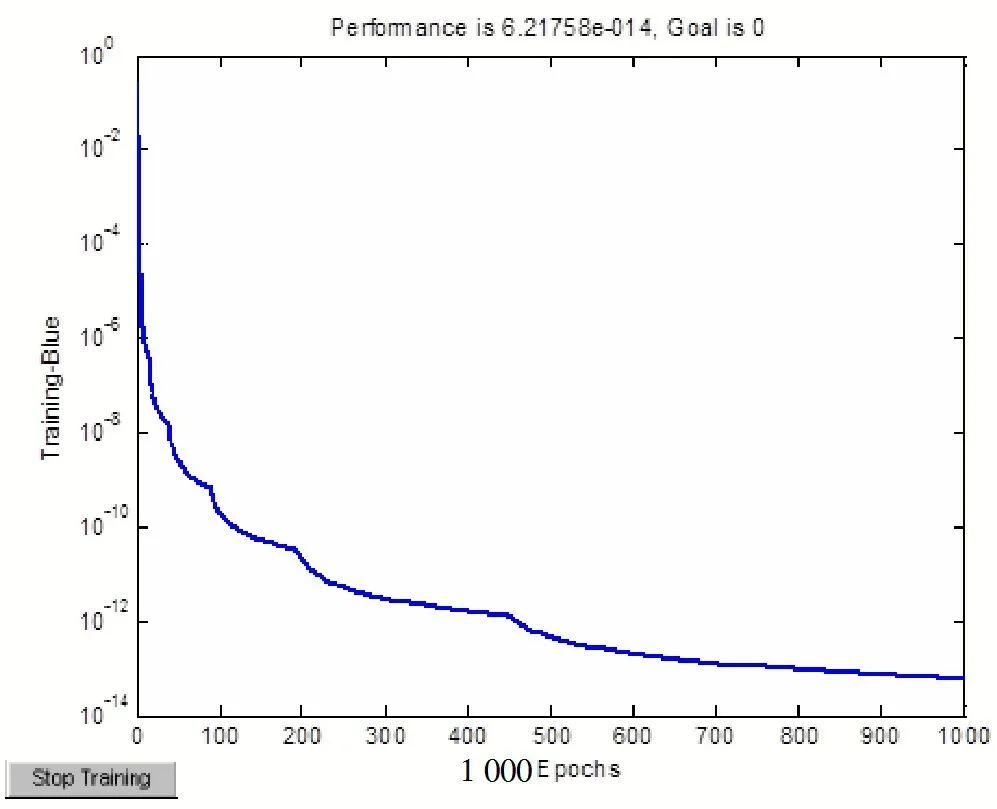
图1 地州市预选网点迭代曲线

y0的每一个输出是按照每一个输入层的数据依次得出来的，所以0.837 8 表示常德市的输出值，0.625 7 表示岳阳市的输出值，0.850 6 表示株洲市，0.683 4 表示湘潭市，0.421 4 表示郴州市，0.588 7 表示张家界市，0.661 7 表示衡阳市，0.577 7 表示怀化市，0.522 0 表示永州市，0.572 1 表示湘西自治州，0.560 1 表示益阳市的输出值。评价值越高，表示在此地建立物流网点越好，将三个学习样本长沙市、邵阳市、娄底市和测试样本即常德市、益阳市等14个市的得分进行排序，结果见表7。

表7 地州市结果排名

通过对现有网点的分析，对其进行打分，分数越高代表这个物流网点的经营越好，所以预测网点的分数越高，代表越适合在这个地方新建物流网点。

2.3 根据BP神经网络得出的结果，选择最后的方案

为了实现公司三年的网络规划目标，首先利用BP神经网络对湖南省的14个地州市进行排名，然后在排名中选择出该市排名最靠前的市区，从而实现公司的网络规划目标，即2018年12月市区网络为30家；2019年12月市区网络新增10家；2020年12月市区网络新增10家。

3 结语

本文基于BP 神经网络物流网点选址模型对物流网点进行了规划设计。以湖南省某物流公司为例，首先根据公司实际情况选取了5个一级指标以及21 个二级指标，并收集湖南省各个市州的二级指标数据。由于数据存在相互影响的关系，难以统一处理，利用隶属度处理得到模糊评价矩阵，再对矩阵进行主成分分析，确定新的决策指标体系，作为BP神经网络的输入端。建立三层BP神经网络，利用该BP神经网络对湖南省各个市的决策指标数据进行处理，得到各个市州的总得分。依据BP神经网络选址模型，得出预选市级网点排名，选择地州市排名靠前的市，逐步实现该公司未来三年的物流网点计划。基于BP 神经网络物流网点选址模型综合考虑了物流网点影响因素的全面性、复杂性，是一种快速、高效的选址方法，可以提高物流网点选址的战略性。