基于纵向滤波的星敏感器低频误差在线估计
2019-10-31叶立军刘付成尹海宁徐樱宝音贺西
叶立军,刘付成,尹海宁,徐樱,宝音贺西
1.清华大学 航天航空学院,北京 100084
2.上海航天控制技术研究所,上海 201109
3.上海市空间智能控制技术重点实验室,上海 201109
人们对卫星姿态确定精度的要求越来越高,目前,卫星姿态测量敏感器精度最高的星敏感器[1-5],是众多航天任务的首选[6],卫星一般会配置两台或多台星敏感器相互备份,为了进一步提高姿态测量精度,一种可行的方式是将两台或多台星敏感器进行数据融合,以获得高于每台星敏感器的姿态确定精度。而多台星敏感器数据融合的前提是消除星敏感器之间的低频误差。
星敏感器低频误差按频率主要可分为3类,第1类表现为星敏感器视场周期[4,7],主要来源是镜头畸变残差,此类误差很难从系统层面补偿,主要通过单机设计减小,其典型误差幅值一般为3″~8″[7];第2类表现为轨道周期[4-12],主要来源是在轨热弹性变形,其误差幅值可达60″[12],某些卫星幅值甚至高达500″[13],一般可通过地面后处理补偿;第3类表现为年周期,主要来源是光行差[7]及地球绕太阳周年变化引起的热环境变化等,光行差可在线校正后可忽略,年周期热环境变化引起的低频误差,短期内一般认为不变,当作常值误差处理。
目前,研究轨道周期低频误差估计的文献很多:庞博等[5]阐述了星敏感器低频误差特点及产生原因,介绍了当前几种主要的星敏感器低频误差的抑制与补偿方法,指出了当前大多数星敏感器低频误差是通过地面处理方式,无法实现误差实时校正,研究适合在轨实时校正方法是具有实际工程意义的。Winkler[14]、Calhoun[15]、Qiu[16]等提出将星敏感器低频误差建模为一阶马尔可夫过程,通过协方差调整对星敏感器的低频误差进行滤除,该方法可用于在轨处理不规律的星敏感器低频误差,但算法精度与地面基于傅立叶级数处理算法相比较差。此外,当星敏感器出现故障后再接入时,由于算法低频误差需要重新估计并收敛,会出现姿态跳变现象,不利于在轨应用。Calhoun[15]、Wang[17]、赵琳[18]、雷琦[19]、熊凯[20]、徐樱[21]、钟金凤[22]等将低频误差建模为傅立叶级数,以离线方式,估计出低频误差傅立叶系数,实现星敏感器低频误差补偿。对于多倍频轨道周期低频误差,傅立叶系数较多,算法计算量大。此外,由于年周期的低频误差存在,为了保证低频误差补偿精度,需要定期对傅立叶系数重新估计并更新,增加了地面工作量。Lei和Yang[23-24]参考了Sarkka[25]的部分成果研究了利用无极卡尔曼滤波(UKF)融合Rauch-Tung-Striebel算法,形成URTS固定区间平滑算法,采用事后处理的方式提高了卫星姿态确定精度,但该算法不适用于在线应用。Iwatat[26]、庞博[27]等通过设置地标观测点,以数据处理的方式实现了星敏感器低频误差的估计和补偿,提高了星敏感器的姿态确定精度,这种方法需要设置地标观测点,只适合地面事后处理。
针对现有公开文献提出算法的不足,本文提出了基于纵向滤波的星敏感器轨道周期慢变系统误差在线估计与补偿算法,可解决星敏感器间轨道周期低频误差在线的在线估计问题,利于实现多星敏感器数据在线高精度融合。
1 星敏感器误差特性
目前针对星敏感器测量误差分析的学者很多,文献[15,17-21]采用多阶傅立叶级数来模拟轨道周期低频误差并作为仿真输入,但均未考虑星敏感器视场周期和年周期低频误差特性因素,不利于客观评价算法的有效性。本文将采用在轨数据作为仿真输入,分析星敏感器低频误差特性。
经曝光时差校正后星敏感器测量四元数保留了星敏感器间低频误差原始信息,根据文献[28]可计算得两星敏感器光轴夹角Z(光轴平转角,体现了两星敏感器非光轴方向测量误差)以及两星敏感器光轴相对旋转角(光轴旋转角,体现了两星敏感器光轴方向测量误差):
(1)
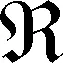
(2)
(3)
式中:⊗表示四元数乘法;q-1为四元数的逆[29];qs1s2为星敏感器s1到星敏感器s2的旋转四元数;qis1为星敏感器s1测量四元数,代表惯性系到星敏感器s1本体系旋转四元数:qis2为星敏感器s2测量四元数,代表惯性系到星敏感器s2本体系旋转四元数。
根据某卫星在轨遥测下传的两星敏感器测量四元数,经式(1)~式(3)计算出两星敏感器光轴平转角和光轴旋转角,与两星敏感器相应的理论角作差后,得两星敏感器1和2(s1和s2)沿光轴旋转角的总误差如图1所示。图中绿色曲线为采用文献[4]中滑动窗口法计算得低频误差(LFE)项。通过图1(a)和图1(b)可以看出,两星敏感器之间低频误差主要体现为轨道周期特性,低频误差峰峰值约为30″。
进一步地,将总误差减去低频误差,可以得到两星敏感器测量噪声,如图2所示。
值得说明的是,图1和图2中的星敏感器误差(含总误差、低频误差、测量噪声)为星敏感器2(待修正星敏感器)相对星敏感器s1(基准星敏感器)的误差。
可以看出,两台星敏感器非光轴方向测量噪声约为7.4″(3σ),光轴方向测量噪声约为50.6″(3σ)。根据噪声不相关原理,且认为两台星敏感器测量精度一致,则可得到单台星敏感器非光轴方向测量噪声约为5.2″(3σ),光轴方向测量噪声约为35.7″(3σ),与单机指标相符,且与文献[30-31]中的结论一致:星敏感器光轴方向测量噪声为非光轴方向测量噪声的6~10倍。
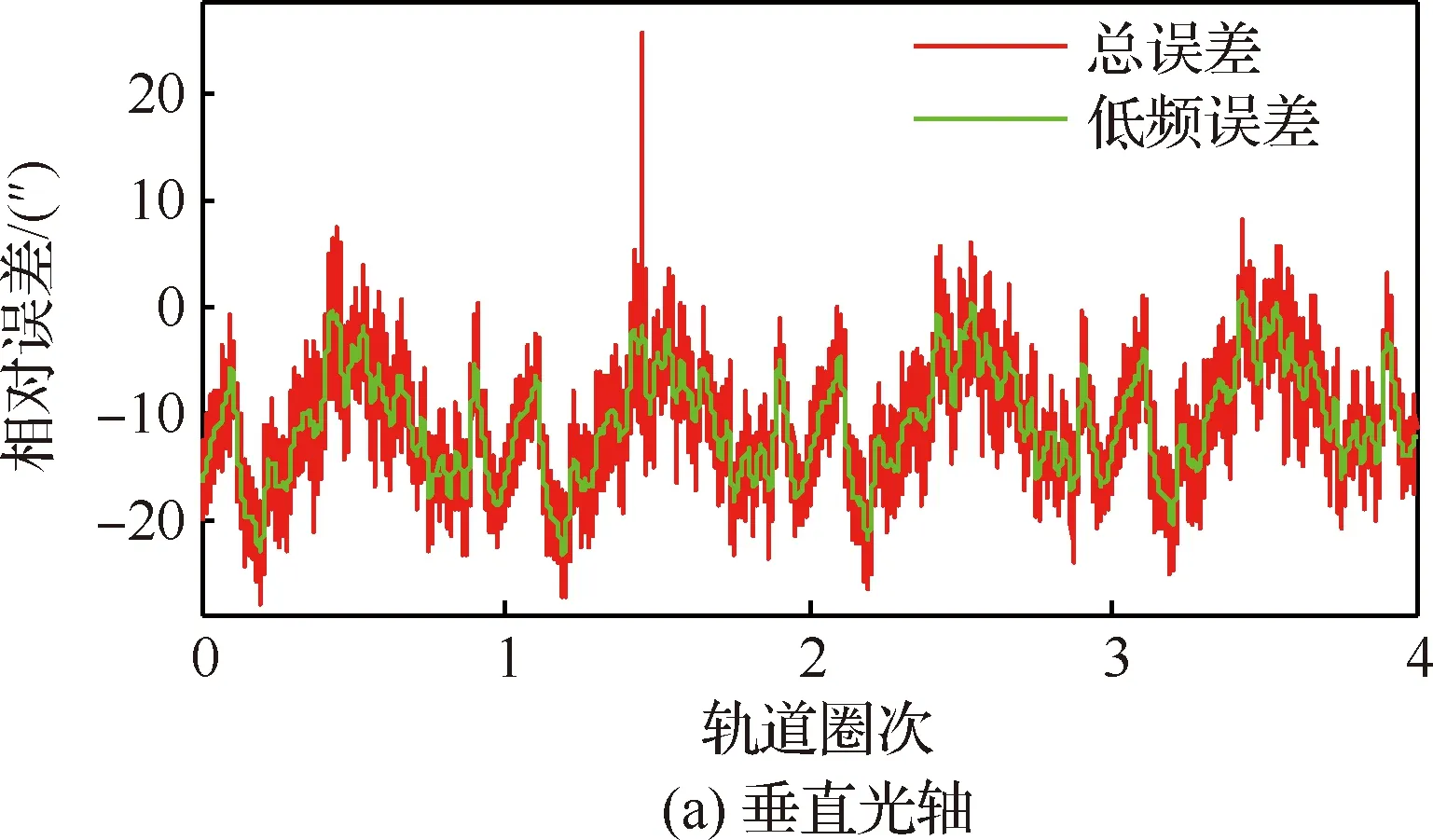
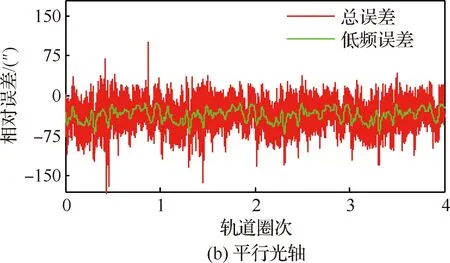
图1 两星敏感器(s1和s2)相对误差
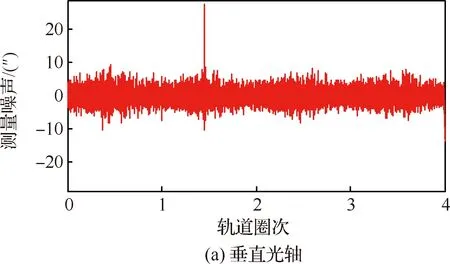
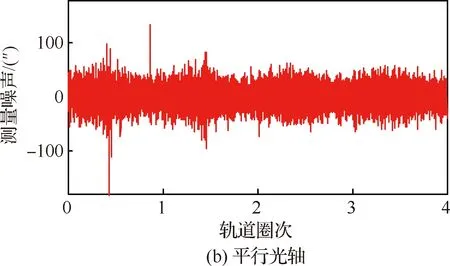
图2 两星敏感器测量噪声
2 算法设计
2.1 估计和补偿策略
星敏感器低频误差估计示意如图3所示,forbit代表轨道圈次。将星敏感器低频误差估计,将轨道幅角等间隔均匀离散为N段,将每段中心点作为特征点,这些点的集合称为星敏感器间低频误差估计表,简称“估计表”。每个估计表的元素均可看作一个估计子模块,每个模块仅估计不同轨道序列相同轨道相位的星敏感器低频误差,并分别估计结果进行存储,最终可将低频误差估计问题变为近常值误差估计问题,采用工程上常用的低通滤波即可实现低频误差无偏估计,得到该点星敏感器间低频误差值。
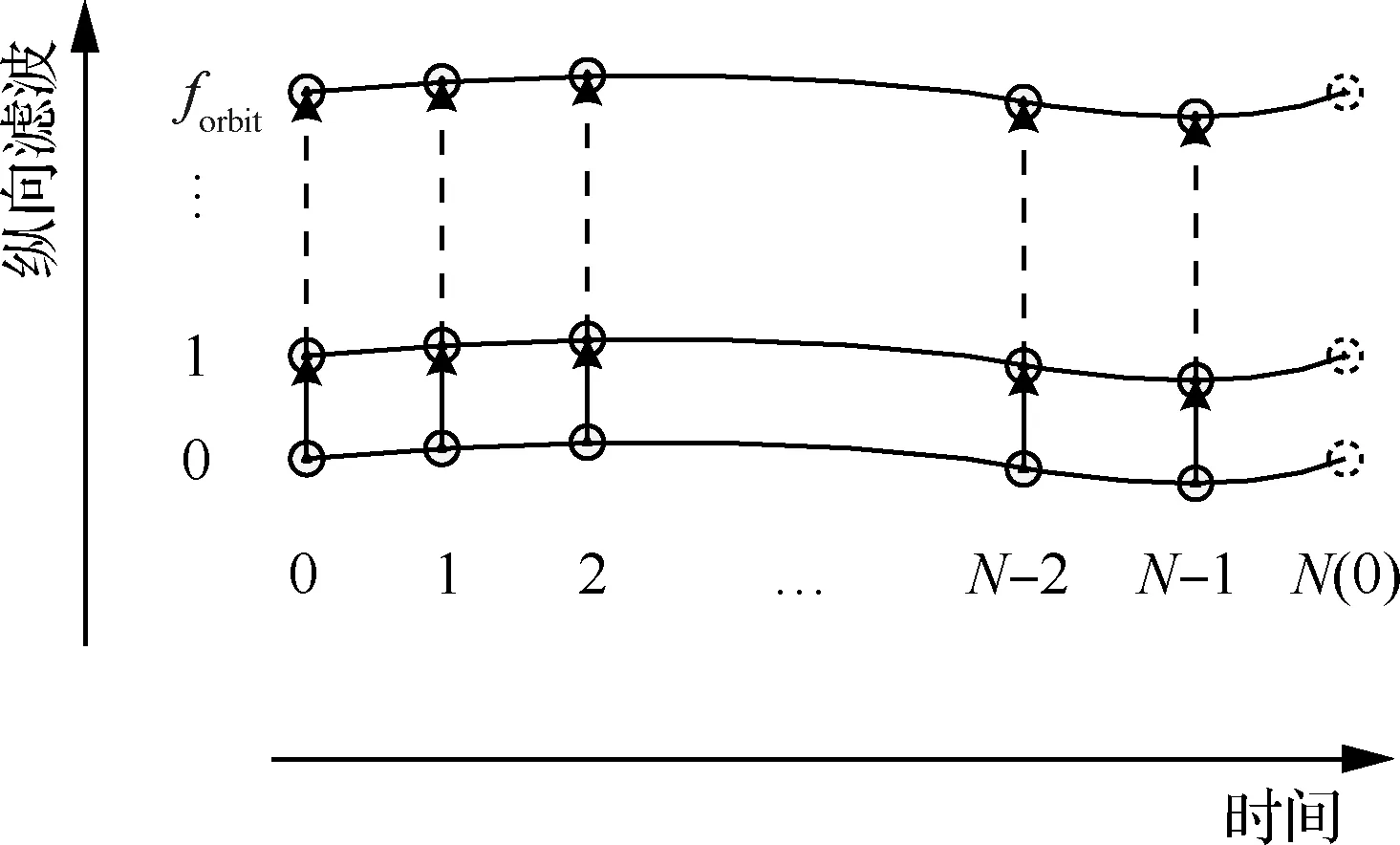
图3 星敏感器低频误差估计示意图
得到估计表后,利用线性插值算法,通过估计表反演出任意时刻当前系统误差并补偿。
2.2 估计和补偿算法
星敏感器间低频误差在线辨识流程如图4所示。图4(a)为星敏感器低频误差估计的主流程,图4(b)为核心算法,是受图4(a)调用的子流程。
算法流程大致分为以下5个步骤:
步骤1对测量点进行采样
在相位点R附近对称取一段数据求平均,提高观测精度,以更进一步提高估计表的估计精度和收敛速度。
相位点R对应的轨道相位计算方法为
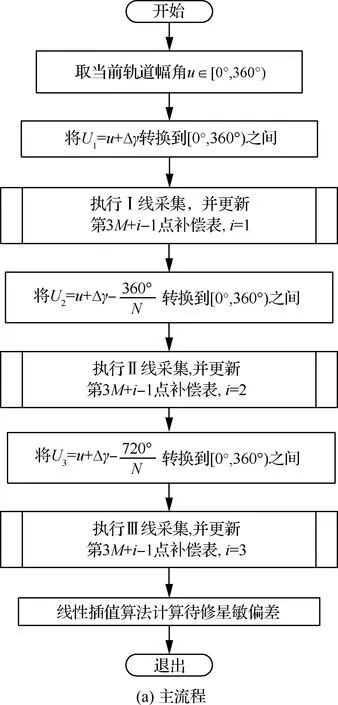
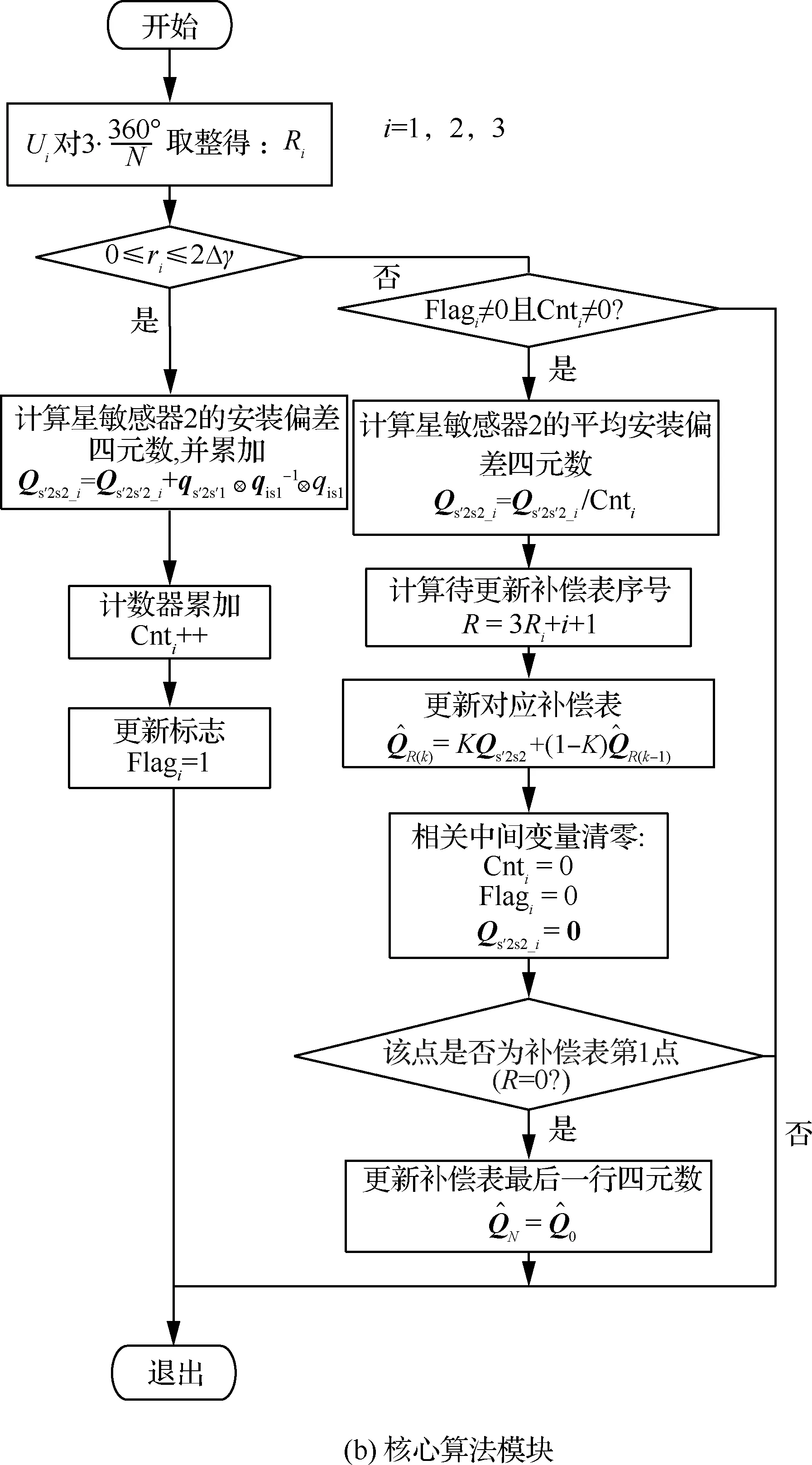
图4 星敏感器低频误差估计流程
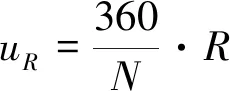
(4)
式中:R=0,1,…,N-1。
步骤2低频误差估计算法
设基准星敏感器为星敏感器1,待补偿星敏感器为星敏感器2,星敏感器2的误差四元数为
(5)
式中:qs′2s′1为从星敏感器2到星敏感器1的理论转换四元数,为已知常值;qs′1s1为单位四元数;化简后可得
(6)
说明:式(6)需要归一化,并进行标量为正的处理。
步骤3基于纵向滤波估计得星敏感器低频误差
第R补偿表更新不再是基于传统的时域滤波,而是基于历史轨道的同一点进行纵向滤波,其表达式为
(7)
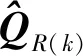
步骤4采用线性插值法计算当前时刻星敏感器2的偏差四元数为
(8)
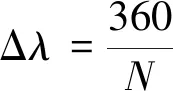
步骤5对星敏感器2测量四元数进行补偿:
(9)
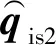
值得说明的是,由于采用线性插值算法,通过线性插值法遍历轨道上所有点,需要0,1,…,N共N+1个点,物理上第N点与第0点为同一点,因此,当更新第0点时,需要同时更新第N点。
2.3 插值误差分析
由于轨道上任何位置均处于“估计表”中某两个相邻点之间,可采用常规的插值算法反演得到任意轨道点的星敏感器低频误差估计值。真实误差曲线为圆弧形,算法采用线性插值算法计算任意点误差,计算误差曲线为折线形,这之间存在的误差称之为“建模误差”。
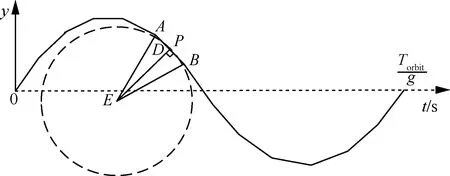
图5 星敏感器低频误差插值误差示意图
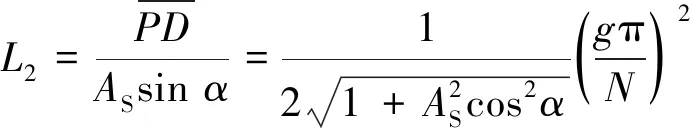
(10)
式中:α为点P所处正弦函数的相位,范围为0~2π。不难看出,α=π/2时,L2取最大值为
(11)
可见,当组成星敏感器低频误差的轨道周期基频阶数g越高,补偿表个数N越少,则插值误差越大,当星敏感器低频误差特性一定时(g不变),随着补偿表个数N的增加,插值误差将以N平方反比关系减小。例如,当g=3时,模型误差要求小于测量误差0.01倍,则根据L2<0.01,可得N>66.6。
注:此处用正弦曲线模拟星敏感器在轨轨道周期低频误差曲线,为近似做法,仅用于评估插值算法误差的影响因素和量级,可指导算法参数设计,无法精确计算插值算法误差,工程设计时需要留好足够裕量。
2.4 补偿点附近采样区选取
补偿点附近采样区以该补偿点为中心左右均匀铺开,弧段损失建模如图6所示。
如图6所示,扩大补偿点附近的采样区,意味着可采更多的采样点,将采样点求平均后可提高该补偿点的估计精度;但反过来,采样区越大,相应的弧段损失也越大,导致该补偿点估计精度降低,因此需要合理选择采样点个数,使补偿点精度最高。
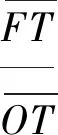
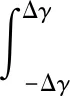
(12)
式(12)化简可得
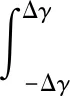
(13)
经泰勒展开,Δγ较小,忽略高阶小量,式(13)可写为
(14)
可看出,所用弧段越小,则弧段损失越小。
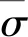
(15)
假设卫星轨道周期为Torbit,则卫星轨道角速度为
(16)
弧段内采样点个数为
(17)
式中:f为系统采样频率。
代入式(15),有
(18)
采样点测量误差为
(19)
对采样点测量误差S求二阶导,可得
(20)
S″>0,说明S有最小值,令
(21)
得最优弧长表达式为
(22)
表1~表3给出一些工程典型工况最优采样弧长对比。

表1 测量误差对最优采样弧长的影响
通过表1对比分析,测量误差越大,同等条件下需要更多采样点以提高精度,所需最优弧长越长。
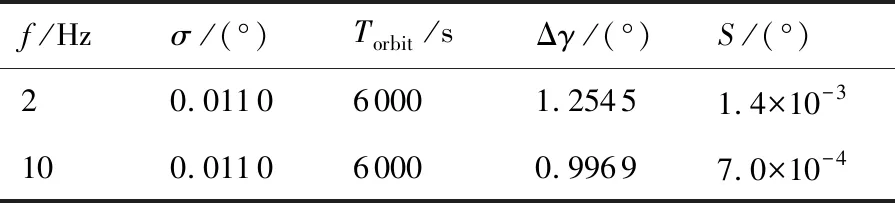
表2 采样频率对最优采样弧长的影响
通过表2对比分析,采样频率越高,同等条件时采样点越多,可降低对采样弧长需求,即最优弧长越短。
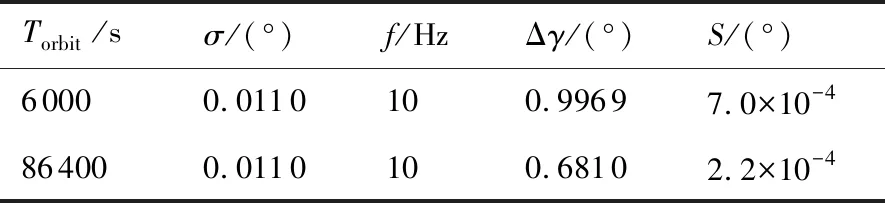
表3 轨道周期对最优采样弧长的影响
通过表3对比分析,轨道周期越长,同等条件下采样点越多,可降低对采样弧长需求,即最优弧长越短。
以Δγ=1°为例说明弧段损失量级:
(23)
可看出,当采样弧段为(-1°,1°),由于弧段损失导致的精度损失比低频误差小约6个量级,可忽略不计。
由表1可以看出,经过优化后,采样值加权平均后,其精度比单机本身测量精度高8~360倍,利于该特征点低频误差精确估计。
2.5 补偿表个数选取
根据2.3节分析,补偿表个数越多,插值误差越小,并可根据精度需要,确定补偿表个数的最低要求。
除了需要满足插值误差足够小要求以外,还需要考虑另外一个问题:一般要求当圈估计的补偿表值需要到一个轨道周期后才能使用,这样通过插值计算的低频误差会是平滑的。否则,当算法首次使用或补偿表值未完全补偿到位时,由于同时使用当圈补偿值与上圈补偿进行插值计算,会引起计算的低频误差出现锯齿波跳变,不利于工程应用。
上述问题可通过设计采样弧长与补偿点个数N来解决,如图7所示。
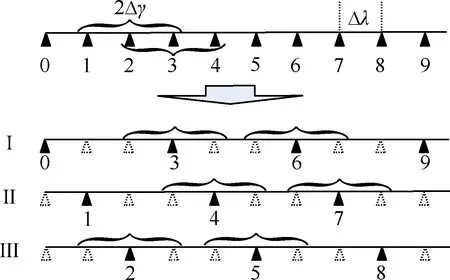
图7 采样弧长与补偿点个数N的关系
图7中,两补偿点间任意轨道相位的轨道周期低频误差需要通过相邻两点补偿表插值得到,两相邻点补偿点间轨道弧长为
(24)
显然,要避免当轨道圈次估计的补偿元素(图7中的第2点)不与上轨道圈次补偿元素(图7中的第3点)混合使用,需满足:
Δλ<Δγ
(25)
此外,为了保证各估计表元素对应的数据采集子模块运行时序,要求两相邻数据采集区不能相互重叠,采用单线采集显然不能满足上述要求,需采用多线采集方式。
根据图7不难看出,最少需要3线(即图7中的Ⅰ,Ⅱ,Ⅲ)采集方式,可以满足上述约束。即:对于Ⅰ线,负责更新第3M点补偿表;对于Ⅱ线,负责更新第3M+1点补偿表;对于Ⅲ线,负责更新第3M+2点补偿表;其中,M=0,1,…,N/3。
采样区边界Δγ取值范围为
(26)
式中:Δλ′=360°/max(M)。
式(26)化简可得
(27)
综合式(24)、式(25)和式(27),可得
(28)
式中:N为3的整数倍的正整数。
根据表1工程典型工况,取Δγ=1.254 5°具有较好的普适性,建议工程选取N=360。
2.6 算法及其稳定性分析
对于某个补偿点来说,星敏感器低频误差估计为离散系统,离散周期为轨道周期Torbit。令
(29)
则式(10)可表示为
(30)
式(30)在频域的表达式为
(31)
可看出,第R补偿点估计值逼近理论值的过程本质上是一阶惯性环节,一阶惯性环节无谐振波,具有绝对收敛性的特性。
此外根据式(29),补偿系数K越大,估计系统时间常数Γ越小。其中,Г为系统修正的时间常数,即估计值达到理论值63.21%所需的时间[32]。
2.7 误差分析及补偿系数选取
根据上述分析,可给出低频误差估计残差δ的表达式,分为两大部分:δ1为一阶系统单位阶跃的逼近过程中的偏差;δ2为星敏感器测量输入的随机误差滤波后的误差。
δ=δ1+δ2
(32)
(33)
(34)
式中:t为算法运行时间;BC为某相位上的低频误差真值;σ为星敏感器测量误差。
可看出,修正的时间常数Г越大,第1部分系统误差δ1越大,同时第2部分随机误差δ2越小。
此外,实际卫星在轨应用时,随着卫星轨道面进动与地球绕太阳公转的共同影响,卫星光照条件还有年周期的特性。本算法还需及时响应低频误差年周期变化特性,例如:要求Tt时间内,修正后低频误差残差与修正前低频误差之比达到ξ,则根据式(33)有
(35)
将式(35)代入式(29),可得
(36)
实际工程使用时,当低频误差中的长期项变化较慢(如年周期),可适当减小K的取值,以进一步提高滤波精度;反之,当低频误差中的长期项变化较快(如天周期),可适当增加K的取值(如K=1),以进一步提高对变化的跟踪响应速度。
3 仿真与分析
3.1 模型误差仿真验证
为了验证算法模型误差,在仿真时仅保留低频误差,不加入基准星敏感器和待修星敏感器测量白噪声,取补偿点个数N=90,补偿表更新系数K=1,修正前后星敏感器残误大小如图8所示。
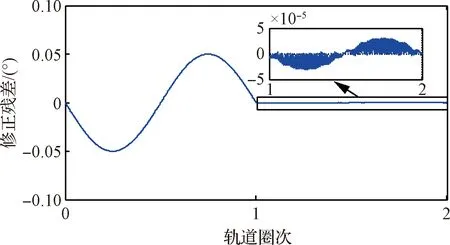
图8 插值误差仿真图
图8中,第1轨道为修正前星敏感器测量误差,第2轨道为修正后星敏感器测量误差,显然,第2轨道星敏感器测量误差是插值误差,可看出,仿真得到的插值误差与原始误差之比为
(37)
理论分析得到的算法误差与原始误差之比为
(38)
可看出,仿真与理论计算的算法误差约为0.26%,证明了理论分析的正确性。
3.2 算法仿真验证
为了验证算法有效性,采用某在轨卫星两星敏感器的原始测量四元数,结合两星敏感器理论安装四元数,根据本文算法,得到星敏感器2低频误差补偿过程,仿真时,为了更好体现中间修正过程,补偿表更新系数K=0.5,根据式(29),系统修正的时间常数Г=Torbit。
经过3个轨道周期(即3Г)辨识与修正,根据式(33),轨道周期低频误差残差为初始值的12.5%,结合第1节星敏感器轨道周期低频误差峰值,本案例仿真数据轨道周期低频误差峰值将从30″减小至约3.75″,与星敏感器视场周期低频误差(3″~8″)相当,基本达到理论上的最佳估计状态,具体仿真情况如图9所示。
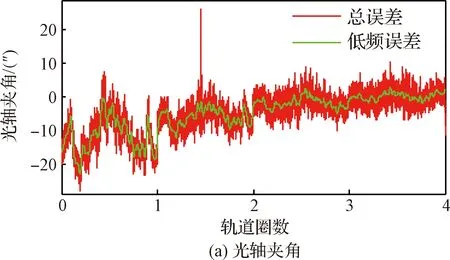
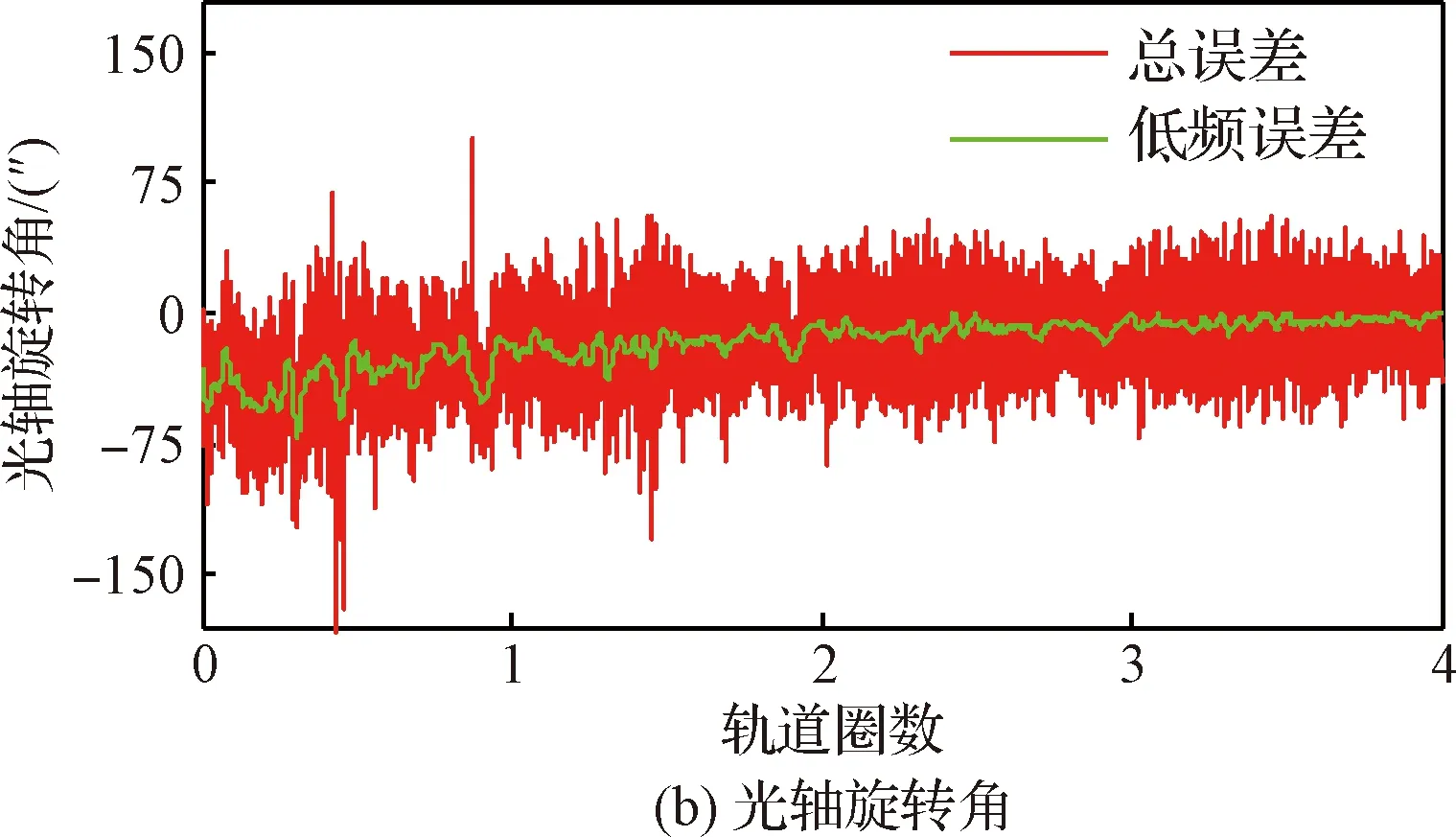
图9 星敏感器低频误差的辨识与补偿过程
图9(a)为两星敏感器光轴夹角,图9(b)为两星敏感器沿光轴旋转角,可以看出,经补偿,星敏感器低频误差中,常值误差和轨道周期误差均明显消除,仅剩下星敏感器视场周期慢变误差。
修正前后,星敏感器测量误差峰值统计值对比如表4所示。

表4 修正前后两星敏感器相对低频误差幅值对比
由表4可看出,基于在轨两星敏感器原始测量四元数,经过本文算法补偿后,星敏感器轨道周期低频误差基本消除。假设两星敏低频误差特性相同且不相关,则修正后单台星敏非光轴方向低频误差为5″,光轴方向低频误差为5.6″,总低频误差为7.5″,修正后误差与星敏感器视场周期低频误差幅值相当,修正效果达到预期。
4 结 论
1) 采取纵向的滤波方法,将轨道平均离散为足够多点,将轨道周期交变的星敏感器低频误差估计问题转换为常值误差估计问题,并采用一阶惯性环节为模型的估计算法,算法收敛,且工程实现简单可靠。
2) 基于本文算法,当某星敏感器长时间故障,仅会使对应补偿表本次数据更新暂停,但该点历史估计数据(理论上为常值)仍有效,任何时刻星敏感器恢复有效并接入本文算法,不会引起算法重新收敛,待估计值无波动,星敏感器之间基准切换均不会引起姿态跳变,利于工程应用。
3) 工程上可以实现轨道周期和年周期(含远大于轨道周期)低频误差的在线无差估计并实时补偿;不适用于星敏感器视场周期(小于轨道周期)的低频误差估计。
4) 基于本文算法,星敏感器轨道周期低频误差会被消除,残余的星敏感器低频误差即为视场周期低频误差,因此本文算法也可用于评估星敏感器视场周期低频误差大小。
5) 在本文算法基础上,配合多星敏感器数据融合算法,可进一步减小系统测量噪声。
