基于优化STD法的大飞机垂尾装配界面精加工过程模态参数识别
2019-10-31赵雄樊伟郑联语刘新玉安泽武杨森
赵雄,樊伟,郑联语,*,刘新玉,安泽武,杨森
1. 北京航空航天大学 机械工程及自动化学院,北京 100083
2. 上海飞机制造有限公司 航空制造技术研究所,上海 201324
垂尾装配接合面(简称装配界面)连接大飞机垂尾和后机身,其对接装配质量直接影响飞机整体气动外形的准确度[1]。为保证对接质量,在总装前需对装配界面进行精加工处理。而装配界面属于低刚度钛合金薄壁件,在精加工过程中易出现振动、变形及根切现象,导致装配界面的精加工质量难以控制。为解决该问题,需对精加工工艺参数进行调整和优化,但该过程严重依赖现场工人的操作经验,具有较大的不确定度。因此,本文基于装配界面精加工过程中的实测振动位移数据提出了一种优化STD模态参数识别方法,通过该方法可快速获取装配界面各阶模态参数,从而为其精加工工艺参数的优选提供更好的科学依据。
常用的结构模态参数识别法可归结为:解析法、有限元仿真法、锤击实验法和环境激励模态识别法。解析法可给出结构动力学特性方程,由该方程能够快速获得结构模态参数,但建模过程复杂,费时费力[2],有时甚至没有理论依据可参考。有限元仿真[3]相比于解析法操作简单,结果展现清晰,适合于复杂结构动力学分析。但在有限元分析过程中往往需对结构进行简化,这样大大降低了模态分析的精度,因此所得模态参数不能反映其模态参数真实值,甚至会得到错误的模态参数。锤击实验法[4]较为常用且识别精度较高,但该方法不仅需要贵重的激励设备,而且容易破坏结构外形轮廓,特别是使用大型力锤锤击过程中很有可能会使加工基准发生偏移,影响工件后续加工过程。而环境激励下模态参数识别法可在激励形式未知的情况下根据实测振动数据获得结构模态参数,分析过程中不仅数据来源真实可靠,而且无需对待辨识的分析模型进行简化。综合分析,对大部件装配界面精加工过程模态参数识别采用环境激励模态参数识别法比较合适。
环境激励下结构模态参数识别法在工业很多领域得到广泛应用,根据信号域的不同可以分为时域法、频域法和时频域法[5]。而常用的环境激励模态参数时域识别法主要有: SSI(Stochastic Subspace Identification) 法[6]、ITD(Ibrahim Time Domain Technique)法[7]及STD(Space Time Domain) 法[8]。其中,SSI法的提出提高了激励未知系统特征辨识的精度,该方法不需要贵重的激励设备,而且不需要中断结构的正常使用就能进行模态参数识别[9]。很多学者对该方法进行了深入研究,比较典型的研究有:付志超等[10]基于SSI法对大展长柔性机翼结构进行模态分析,结果表明,该方法可较为精确地获得其的动力学参数。同理,张永祥等[11]基于SSI法构造了平板结构的2个不同维度的Hankel矩阵模态模型,进而剔除虚假极点,获得平板结构的高清稳态图,并进行谱系聚类分析,最终准确识别出平板结构的模态参数。Boonyapinyo等[12]基于数据驱动的SSI法对大桥振动现象进行了研究,给出桥面模态参数,并由此对桥面截面形状进行了优化。李团结等[13]通过降低Toeplitz矩阵中可控反转矩阵的维数来减小SSI法的计算量,但计算效率仍相对较低。为能进一步提高计算效率,避免矩阵计算而耗费大量时间,计算效率较高的环境激励下结构模态参数识别方法得到了推广。如ITD法利用结构振动时域信号进行模态识别,避免构造Toeplitz矩阵及其SVD分解耗费较长的计算时间。Yang等[14]通过ITD法识别出了滚动轴承模态参数,并以此判断轴承工作状态和故障类型。STD法在ITD法的基础上进行了改进,避免对系统特征矩阵进行QR分解,进一步提高了计算效率。杜飞平等[15]利用STD法获得了火箭液体发动机的模态参数,实验证明,该方法具有较高的识别精度和效率。ITD和STD法皆能够高效识别出结构的模态参数,但在识别过程中往往会使用随机减量技术进行数据预处理,从而造成结构的某些模态丢失。针对该问题,杨佑发等[16]将协方差驱动SSI法中Toeplitz矩阵的数据作为ITD法的数据输入,从而保留了原始数据的所有信息,避免了数据前处理造成信息丢失。张小宁等[17]利用SSI法并结合模态置信因子及模态保证准则剔除虚假模态,实现结构模态参数的自动识别。以上环境激励模态参数识别方法均在实际系统的特征分析中得到了应用,但应用对象大都集中在楼宇、桥梁、船舶、火箭等大型结构中,应用场景大都集中于结构运行过程中,而很少应用在航空航天大型薄壁件的加工过程中。而且SSI法模态辨识的精度相对较高,但识别效率较低。STD法模态辨识的效率较高,但在模态参数识别的过程中会损失一定的识别精度。
综合考虑,本文基于STD法原理及Toeplitz矩阵并结合模态置信因子及模态保证准则,提出了一种面向飞机垂尾装配界面精加工过程的优化STD模态参数识别法。该方法通过对装配界面精加工过程振动位移数据的分析和处理,可准确高效地获得其模态参数,为装配界面精加工工艺参数的合理选择提供一定的理论依据。
1 大飞机垂尾装配界面及其精加工系统
如图1(a)所示,大飞机垂尾装配接合面由平面和多孔配合的2.5D制造特征构成,其精加工工艺过程主要包括接合面的铣削和连接孔的镗削及钻削。该装配接合面共有8块形状尺寸类似的子装配界面(图1(b))构成,并按图1(c)所示的方式对其进行装夹。装配界面精加工系统主要由数控定位调姿系统、主动夹紧系统、数控系统、在机测量系统和外部激光跟踪仪测量系统等子系统组成。其中,调姿定位系统用于垂尾大部件的定位和位姿调整;待调姿和定位完成后,夹紧系统对装配界面施加一定夹紧力使其在精加工过程中保持稳定,如图1(d)所示。
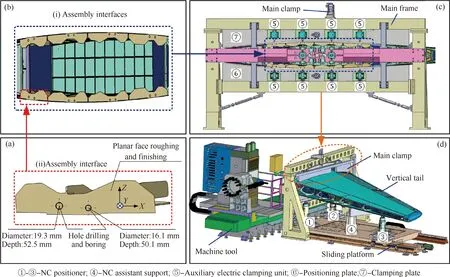
图1 大飞机垂尾装配界面精加工系统
装配界面几何尺寸大、结构刚度低,在动态铣削力作用下会产生明显的振动现象,容易造成装配界面的精加工质量较差,甚至会出现废品现象,造成不可估量的经济损失。为解决该问题,车间现场一般采用人机交互的方式调节装配界面的精加工工艺参数以减少加工振动对精加工质量的影响,但该调节过程严重依赖工人的操作经验,缺乏理论依据、费时费力,严重降低了装配界面的精加工效率。为此,本文提出一种优化STD模态参数识别法,利用该方法可快速获得装配界面各阶模态参数,并据此辅助精加工工艺参数的调整,使得调整过程更为明确,从而提高精加工效率。
2 优化STD法模态参数识别原理
基于传统STD模态参数识别法,优化STD法主要在以下两个方面进行优化:一是数据预处理方式的优化,即利用实测振动位移数据进行协方差计算构造Toeplitz矩阵,并将该矩阵中全部数据项作为STD法的输入数据;二是识别结果可靠性判别方式的优化,即利用模态置信因子κ,结合模态保证准则(Modal Assurance Criterion,MAC)对模态参数稳定性进行辨识,选择其中模态参数稳定性最高的辨识结果作为工件的模态参数。
2.1 优化STD法构造原理
优化STD法首先利用工件加工过程中的实测振动位移数据构造Hankel矩阵,进而构造Toeplitz矩阵,并将其作为STD法的输入数据,然后,根据STD法原理识别工件模态参数,具体过程可分为以下3个步骤:
步骤1Toeplitz矩阵的构造
首先,利用工件加工过程产生的振动位移数据构造Toeplitz矩阵,这样不仅可以保留数据中的所有信息项,同时还可以去除噪声信号的影响。因此,在传统STD法中引入Toeplitz矩阵进行数据预处理,可有效提高工件加工过程模态参数的识别精度。为此,首先由实测振动位移数据构成Hankel矩阵为Y0|3M-2,表达形式为
(1)
式中:yi(i=0,1,2,…)为实测振动位移响应值;Yp为y0~y2M-2构成M×M的上Hankel矩阵;Yf为yM~y3M-2构成M×M的下Hankel矩阵。
将上、下Hankel矩阵中所有实测振动位移响应值进行协方差计算,所得序列构成Toeplitz矩阵为T,表达形式为
(2)
上述协方差计算过程中可消除环境噪声的影响,从而较为准确地提取出工件自由振动响应信号。因此,可将该协方差序列近似的代替自由振动响应信号作为优化STD法的输入。
步骤2工件动力学特征矩阵的求取
设工件有M阶模态,而一般测量过程中振动数据的实测点个数要远小于工件的实际模态阶次。以一个实测点为例,为准确获得各阶模态参数,需要将某一时间段内的振动数据延时M-1个Δt时刻,获得M-1个虚拟测点,从而构造具有M个测点的振动响应矩阵并求取模态参数。
根据动力学原理,工件自由振动响应的运动微分方程可表示为
(3)
式中:M、C、K分别为工件的质量矩阵、阻尼矩阵及刚度矩阵。
据式(3),其解可表示为
xM×1=ΦM×M·exp(srt)M×1r=1,2,…,M
(4)
式中:x、Φ分别为工件自由振动响应的位移向量和模态振型矩阵;exp(srt)M×1为由特征值构成的向量的e指数表达式,r表示第r个特征值。
因此,由实测数据构成的工件自由振动的响应矩阵可表示为
XM×M=ΦM×M·ΛM×M
(5)
式中:XM×M为M个测点构成工件的M个时刻的自由响应矩阵;Λ为由工件模态特征值构成的矩阵。
将工件自由振动响应矩阵延时Δt后得到其振动延时响应矩阵为
(6)

(7)
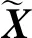
步骤3装配界面模态参数的识别
令Δt=Ts,Ts为采样周期,由式(2)可知,T的第M行由其第M-1行延时Ts之后得到,即
TM(t)=TM-1(t+Δt)=TM-1(t+Ts)
(8)
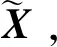
(9)
由式(8)和式(9)可得矩阵B的表达式为
(10)
显然,B是只有第M列元素未知的Hessenberg矩阵。由式(9)可知
(11)
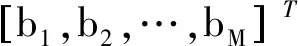
则b的最小二乘解用伪逆法可表示为
(12)
将b代入B,可得
B·Q-1=Q-1·α
(13)
式中:α为特征值对角矩阵;Q为三角矩阵。
式(13)可得到矩阵B特征值为
Vr=exp(srTs)r=1,2,…,M
(14)
式中:Vr为特征值向量的e指数表达式。
对式(14)两边取对数,有
Rr=lnVr=srTs
(15)
由式(15)可分别求得工件的各阶模态频率ωr和阻尼比ξr分别为
(16)
(17)
进而根据式(14)求出工件的各阶模态振型Arp为
(18)
由式(9)和式(10)可知,相比于传统STD法,优化STD法不仅可利用实测振动数据构造出Toeplitz矩阵来提高模态参数的识别精度,而且可以避免对特征矩阵B进行QR分解,使得计算量大为降低,因此能够提高计算效率。
2.2 优化STD法自动定阶原理
传统环境激励模态参数识别方法主要依据奇异值跳跃法及稳定图法对结构模态进行定阶。而这两种方法均需人为参与,易将带有噪声的模态参数标定为工件的模态参数。
为解决该问题,本文基于优化STD法,并结合模态置信因子κ和模态保证准则MAC自动剔除工件的虚假模态,进而实现工件模态参数的自动定阶。自动定阶过程可分为以下4个步骤:① 设工件模态阶次依次为1,2,…,rmax,各阶次分别包含1,2,…,rmax阶模态参数,rmax≥M,求取工件1~rmax各阶次模态参数,并以此构造模态频率下三角矩阵ω;② 根据ω,求得相邻阶次的模态置信因子κ,并初步选择其中κ最大的m个阶次按升序方式排列;③ 求上述m个阶次的模态保证准则之和∑MAC(相邻阶次的前r阶振型模态保证准则之和);④ 选择其中κ·∑MAC最大的阶次作为工件的模态阶次,具体过程如下
步骤1模态参数下三角矩阵的求取
通过式(16)~式(18)求出的工件模态参数,构造出ω的表达形式为
(19)
式中:ωa,b为具有a阶次工件的第b阶模态频率;b≤a。
步骤2相邻阶次模态置信因子的计算
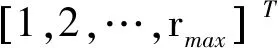
κ=root(h(ω))
(20)
式中:κ为模态置信因子构成的矩阵;root(·)为求根公式;h(ω)代表模态置信因子函数。
从κ中由大到小选择其中m个模态置信因子κi.i+1,κj,j+1,κk,k+1,…(共m项),并求其对应的阶次ri.i+1,rj,j+1,rk,k+1,…(共m项) 及各阶次所对应的模态参数,建议m取值至少大于3。
步骤3相邻阶次模态保证准则之和的求取
通过κ的筛选,获得模态频率置信度最高的m个阶次,这m个阶次可看作是频率稳定的阶次,但其中可能包含环境噪声模态。针对该问题,对这m个频率稳定的阶次进行振型稳定性判定。振型稳定性可用MAC定义,即
(21)
式中:φa,j为具有a阶次工件的第j阶模态的振型向量;φb,j为具有b阶次工件的第j阶模态的振型向量;b=a+1。
MACa,b的值处于0~1之间,其值的大小表示阶次a和b模态振型的相关性。当MAC=0和1时分别表示这两个模态振型之间完全无关和相关;将m个频率稳定的阶次按阶次大小升序排列,求取相邻、阶次模态振型的MAC之和为
(22)
步骤4工件最佳模态阶次的确定
计算κi·∑MACi,i=1,2,…,m-1,该值最大时对应的阶次即为工件的模态阶次。其所对应的频率、阻尼比以及振型即是工件的模态参数。
总之,通过κ选择出频率稳定性较高的模态阶次,通过∑MAC选择出振型稳定性最高的模态阶次,最终通过κ·∑MAC确定工件的真实模态阶次,经过两次筛选保证最佳阶次的唯一性及模态参数的准确性。环境激励下模态参数识别法通过数据协方差计算、模态置信因子及模态保证准则3个过程减小噪声干扰,提高工件的模态识别精度。依据上述原理,利用垂尾装配界面精加工过程中的振动数据对其进行模态参数识别。
3 垂尾装配界面模态参数识别
大飞机垂尾装配界面由钛合金Ti6-Al4-V制成,属于难加工材料。其材料参数为:密度为ρ=4.48×103kg/m3,弹性模量为E=1.14×1011Pa,泊松比为υ=0.33[18]。由于每块装配界面的边界约束条件和实际加工工况相同,不失一般性,选其中一块装配界面作为样件进行实验研究,实验系统设置如图2(a)所示,并采用图2(b)所示的数据采样系统来采集和处理装配界面的振动响应数据,采样频率设置为2 000 Hz。该数据采样系统主要由加速度传感器(INV9832-50、灵敏度为99.563 mV/g、频率范围为20~10 000 Hz)、数据采集仪(INV3062V2、24位网络式智能采集仪)和数据处理系统(Coninv DASP-V11)等组成。
为准确获得装配界面各阶模态参数,首先利用图2(c)所示的切削实验方法来获取装配界面的精加工振动响应加速度数据,基于该数据并采用上述优化STD法对装配界面进行模态参数识别。然后,根据装配界面模态参数辅助其精加工工艺参数的调整。最后,设计对比实验验证优化STD法模态参数识别精度。
3.1 优化STD法模态参数识别
对装配界面进行切削实验模拟其精加工过程,并对该切削过程的振动响应数据进行分析研究。精加工时选择直径为50 mm、刀具齿数为6的端面盘铣刀;根据加工工艺知识和实际操作经验,精加工铣削工艺参数设定为:主轴转速为300 r/min,轴向切深为0.3 mm,进给速度为120 mm/min;为保证加工质量和减少刀具磨损,采用顺铣往复行切走刀的加工方式。同时,综合考虑数据的有效性及实验的经济性,仅选择对振动响应比较敏感的点2、3(见图4)作为振动信号拾取点,采集其法向切削振动信号,并对采集的振动加速度信号作积分处理,以5 s作为采样时间,得到图3所示的装配界面振动响应加速度和位移的时域信号。

图2 装配界面模态分析实验设置图
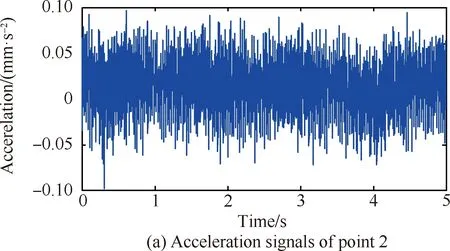
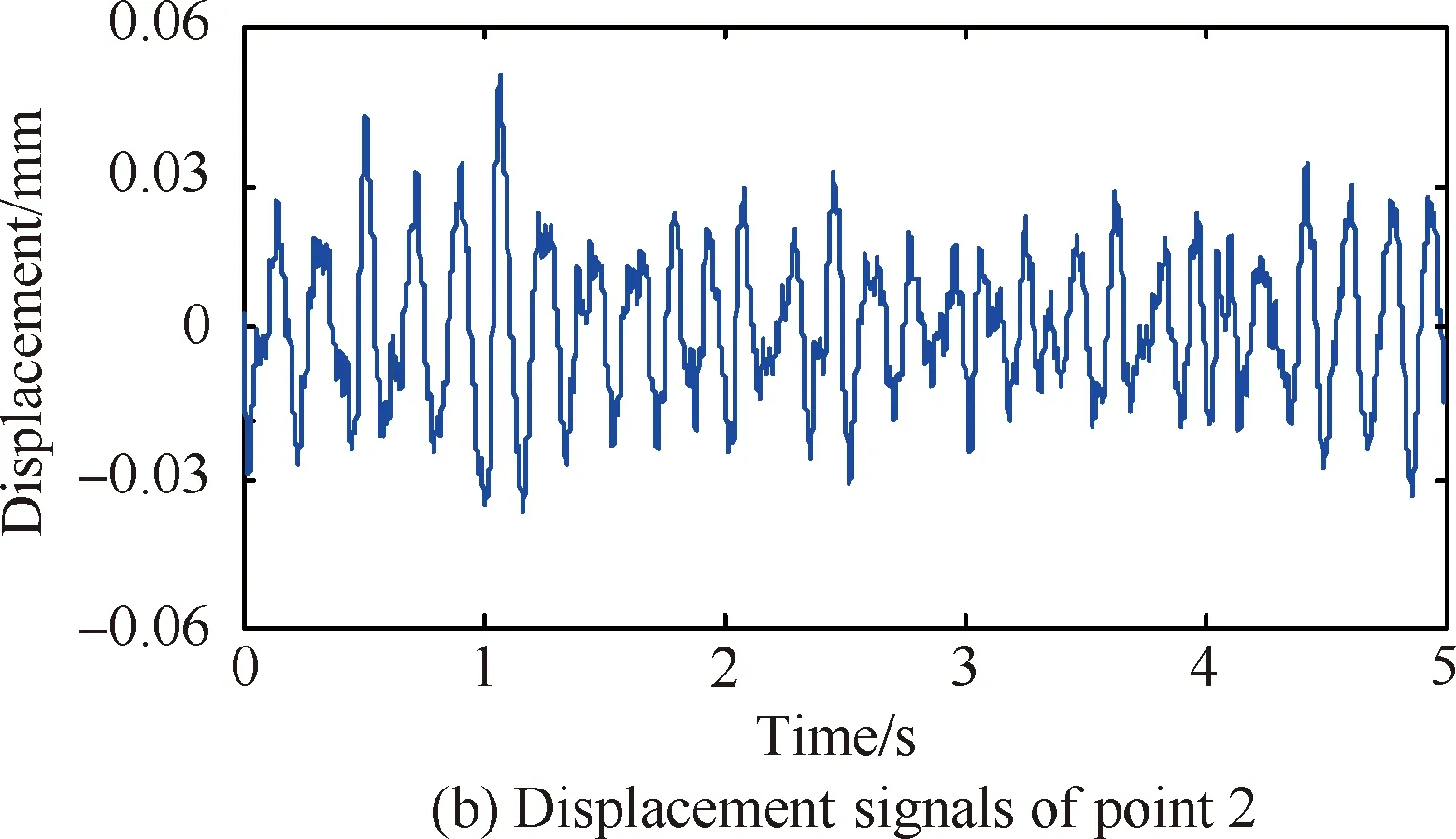
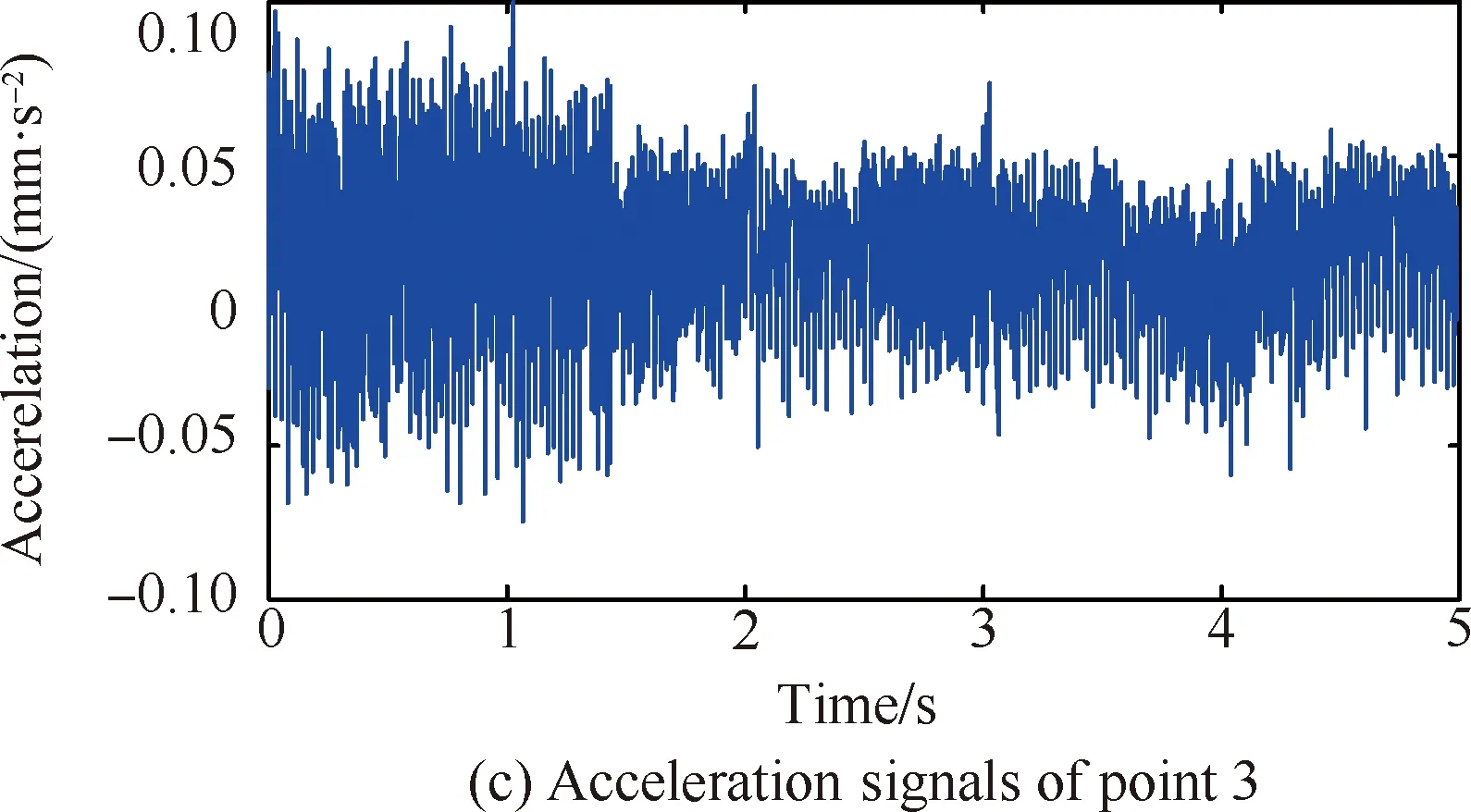
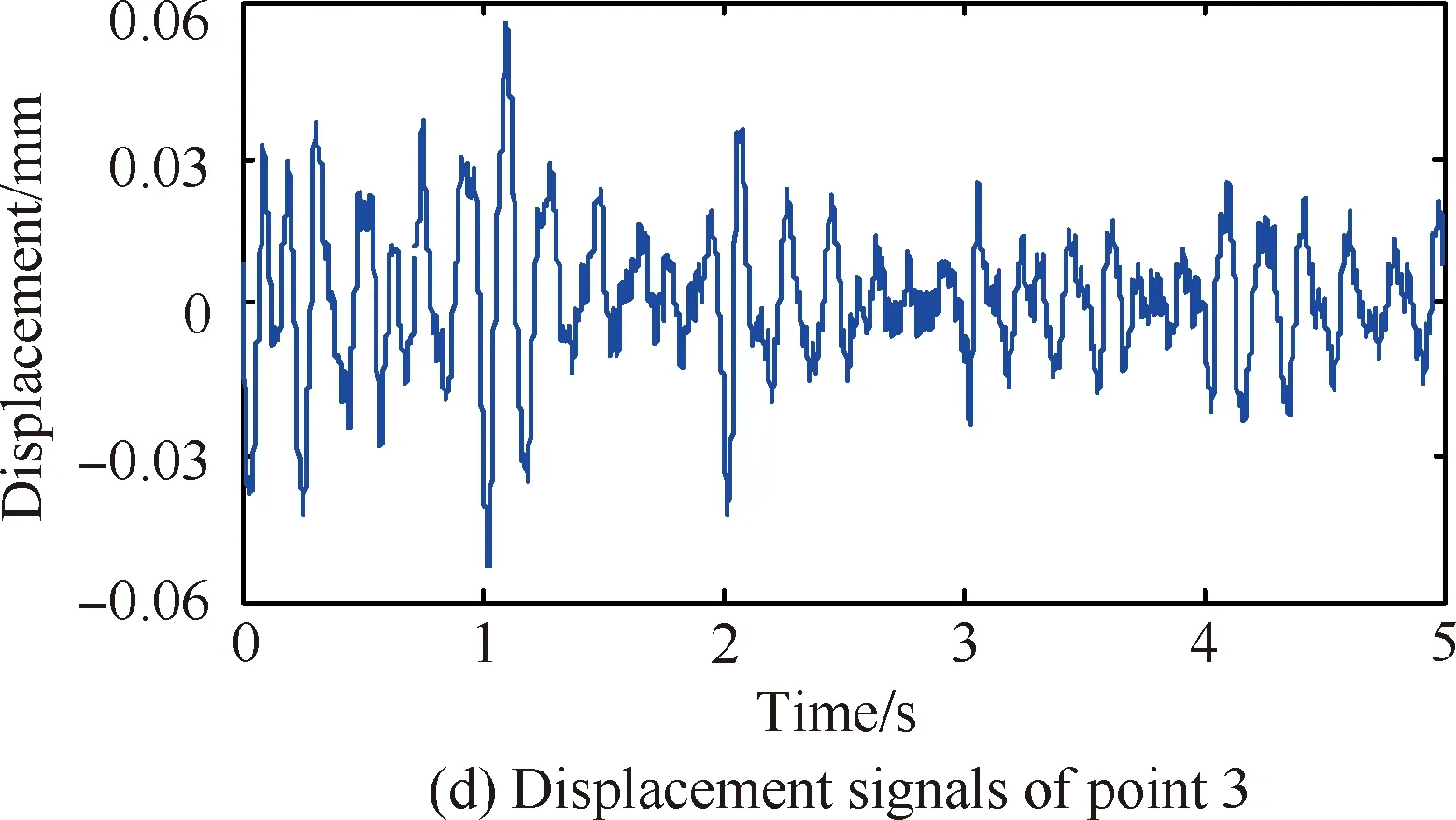
图3 精加工过程中测点2、3振动加速度、位移数据
由图3(d)可以看出,测点3的振动位移幅值较大,最高可达0.06 mm,因此基于测点3的振动位移数据,运用优化STD法对装配界面进行模态参数识别。首先利用测点3的振动位移数据构造40×40的Toeplitz矩阵,取其1~39行及2~40行数据作为STD法的输入数据,求取装配界面各阶次模态参数并构成下三角矩阵ω;然后根据自动定阶原理,用15次多项式对模态阶次矩阵R与ω进行插值拟合,进而求取模态置信因子函数的根对应的阶次和相应的模态置信因子;其次选择其中6个模态置信因子最大的阶次作为频率稳定的阶次,并按阶次大小升序排列;最后求取相邻阶次的∑MAC,选择其中κ×∑MAC最大的阶次作为装配界面真实的模态阶次。
一般,装配界面前6阶模态参数在其动力学特性中起主要作用,为此选择其前6阶模态参数进行对比分析,表1给出了装配界面通过优化STD法识别所得各阶模态频率ω及阻尼比ξ。
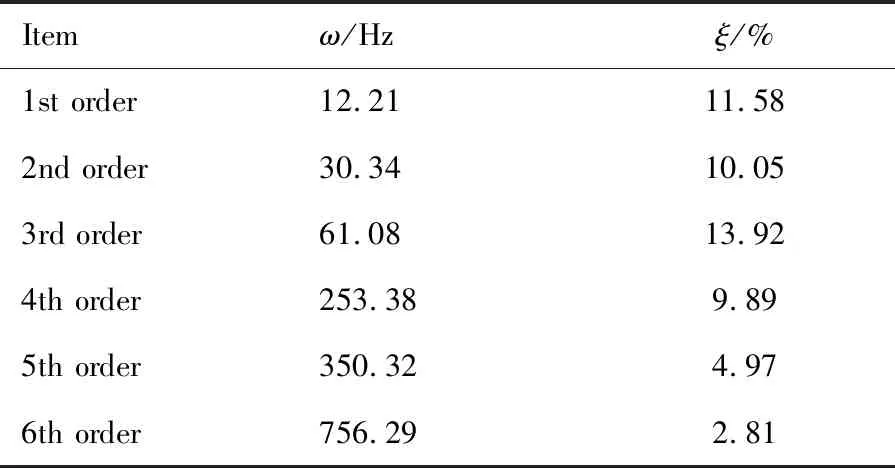
表1 优化STD法模态参数辨识结果
据表1可知,为避免精加工过程中发生共振现象,依据铣刀激励频率与转速之间的关系式ft=N·f=N·n·z/60(N=1,2,…)(ft为铣刀对装配界面的激励频率,N=1时,为铣刀激励主频率,N>1时,为激励谐波频率;n为主轴转速;z为铣刀齿数),可得n取值时应使ft避开各阶模态频率,即:n≠60·fm/(z·N)(N=1,2,…),式中:fm为各阶模态频率及其领域值。由于装配界面各阶模态阻尼比较小,可考虑减小轴向切深或施加阻尼器来减小其铣削振动。
3.2 优化STD法模态参数识别精度分析
为验证优化STD法的可行性及有效性,首先将标准锤击法得到装配界面的模态参数作为其测量参考值,并将优化STD法识别的模态参数与其进行对比,以验证优化STD法的可行性;然后基于测点3振动位移数据,将优化STD法的识别结果与传统STD法及SSI法的识别结果进行对比,以验证优化STD法的有效性,详细过程如下:
1) 利用标准锤击法对装配界面进行模态参数识别。该方法采用力锤(INV9310,量程为500 N,灵敏度为10 mV/N)作为装配界面的激振源。由于装配界面几何尺寸较大,为能覆盖所有关键特征点,选择如图4所示的28个关键分布点作为锤击点,同时采集测点2、3的振动响应数据。由于篇幅限制,只给出敲击点1时,点2、3的动态振动响应数据,如图5所示。
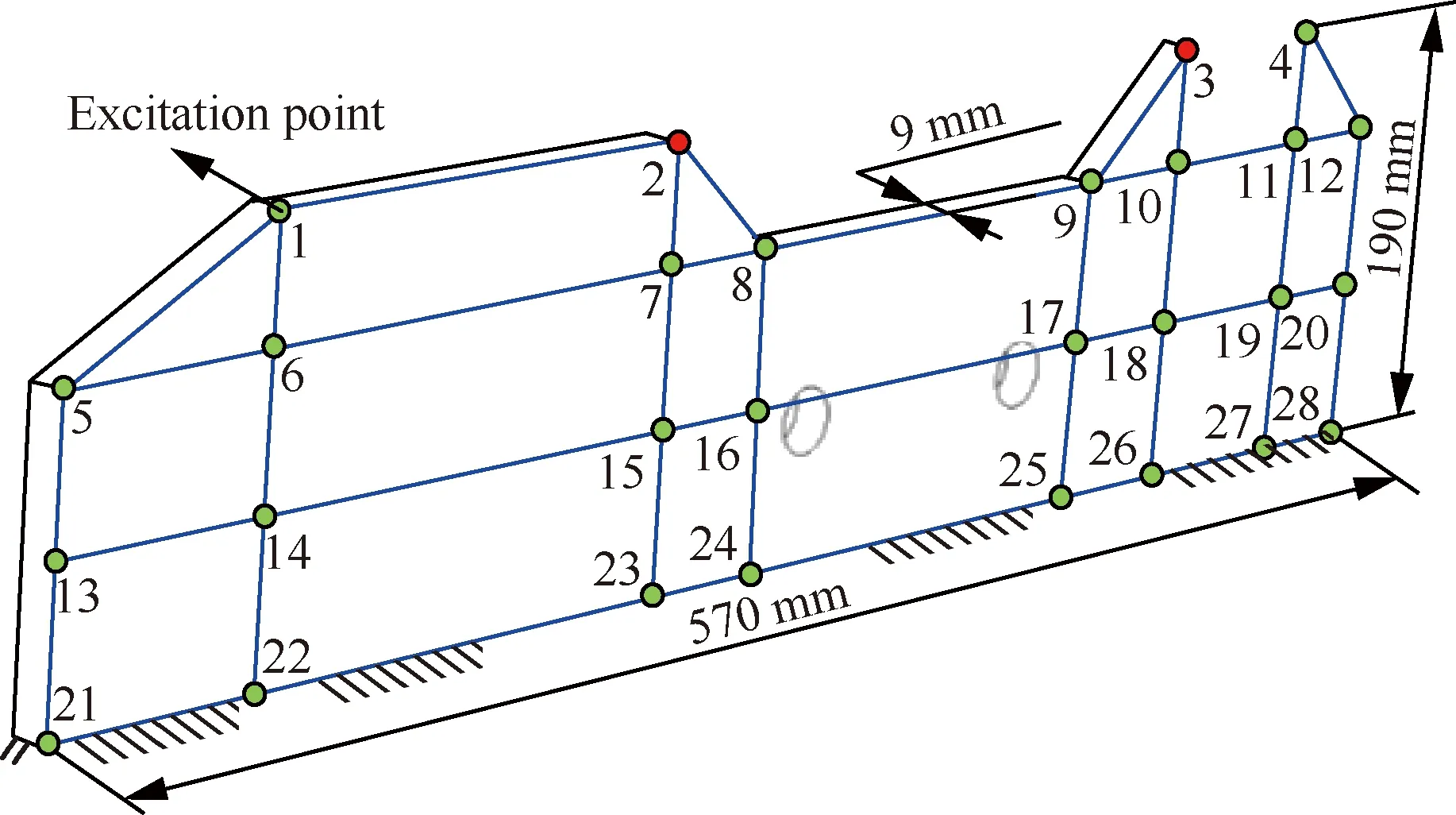
图4 装配界面的锤击测试原理图
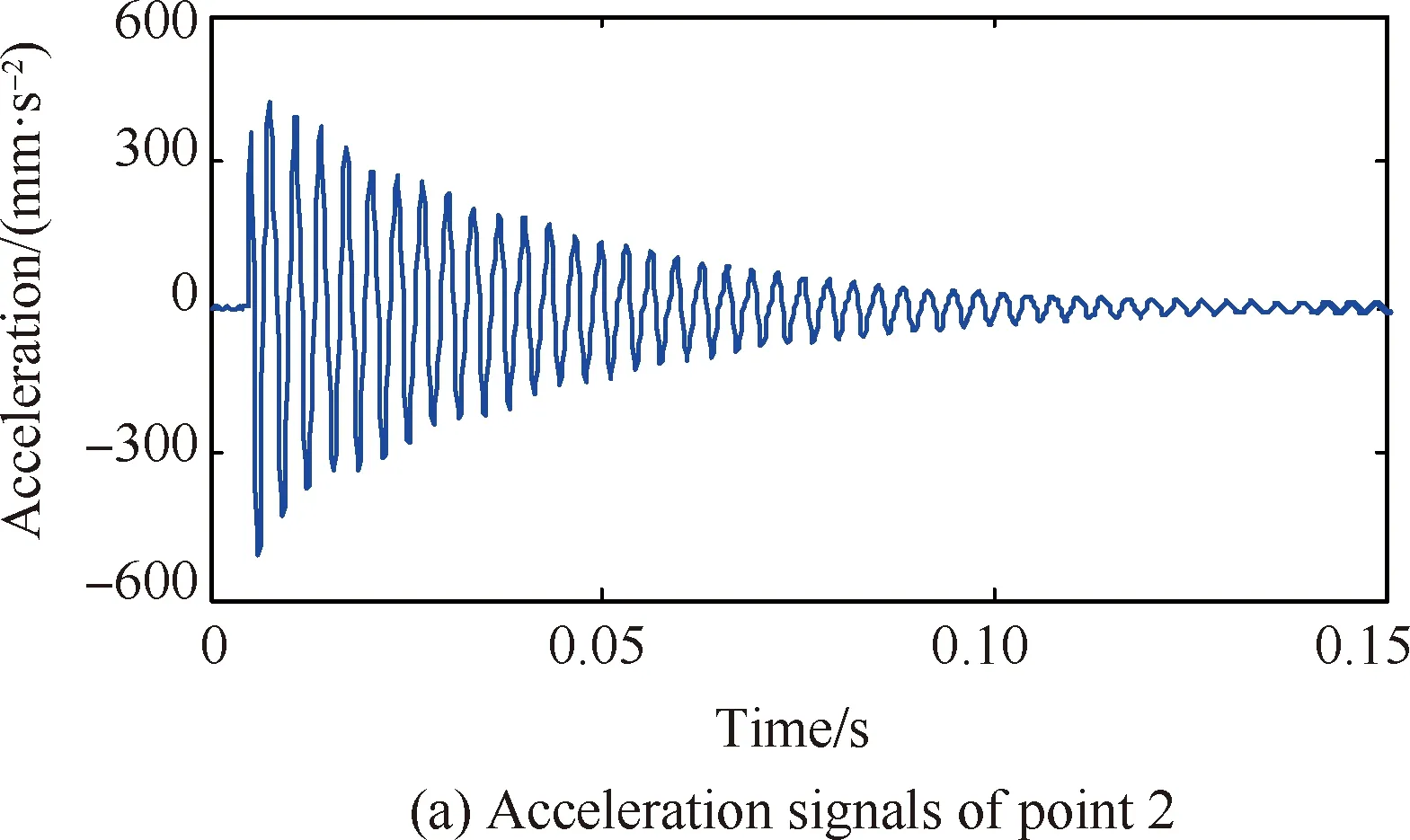
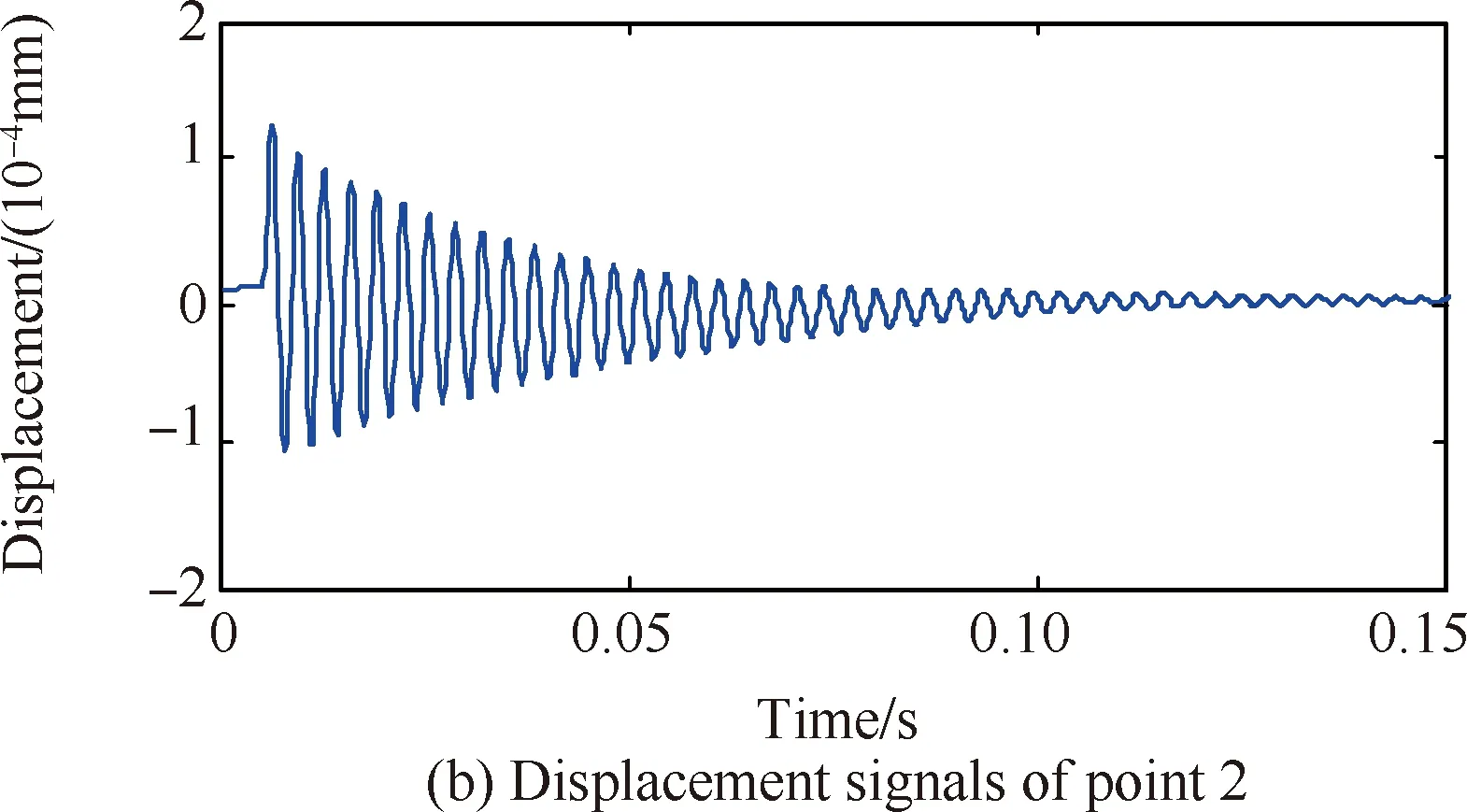

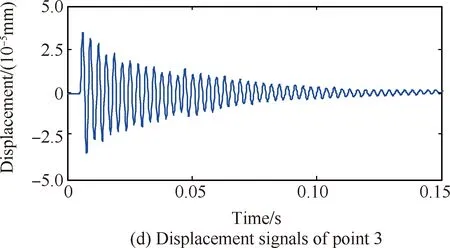
图5 锤击测试中测点2、3振动加速度及位移数据
3) 运用传统SSI法对装配界面进行模态参数识别。利用实测振动数据构造两个40×1 000的Hankel矩阵,进而构造40×40的Toeplitz矩阵,对该矩阵进行SVD分解及QR分解求取装配界面模态参数。
表2给出了经上述3种方法获得的装配界面各阶模态参数。对表中的各阶模态参数进行分析,并计算出传统STD法、SSI法和优化STD法识别结果与装配界面各阶模态参数测量参考值之间的误差值,如表3所示。
以装配界面的一阶模态频率识别结果为例进行分析,从表3中的误差数据可看出,优化STD法、传统SSI法和传统STD法模态频率识别结果与装配界面模态参数测量参考值之间的误差分别为:4.76%、8.58%和17.47%。相比于传统SSI法和传统STD法,优化STD法的模态频率识别精度分别提高了3.82%和12.71%;同理,其余各阶模态频率及阻尼比的识别精度均有不同程度的提高。由上述过程可以看出优化STD法在不干扰装配界面正常加工的情况下可快速准确地获得其各阶模态参数,从而验证其可行性可有效性。
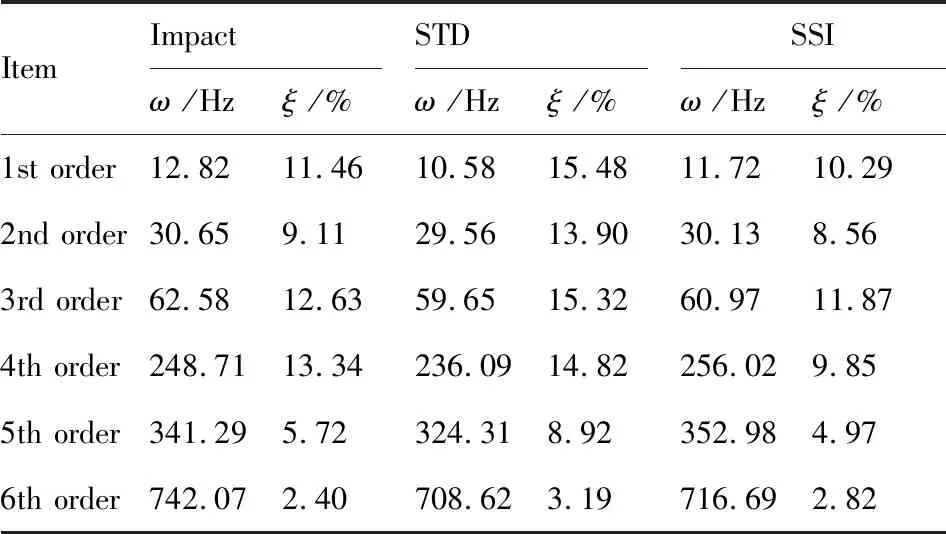
表2 锤击法、STD法和SSI法模态参数识别结果
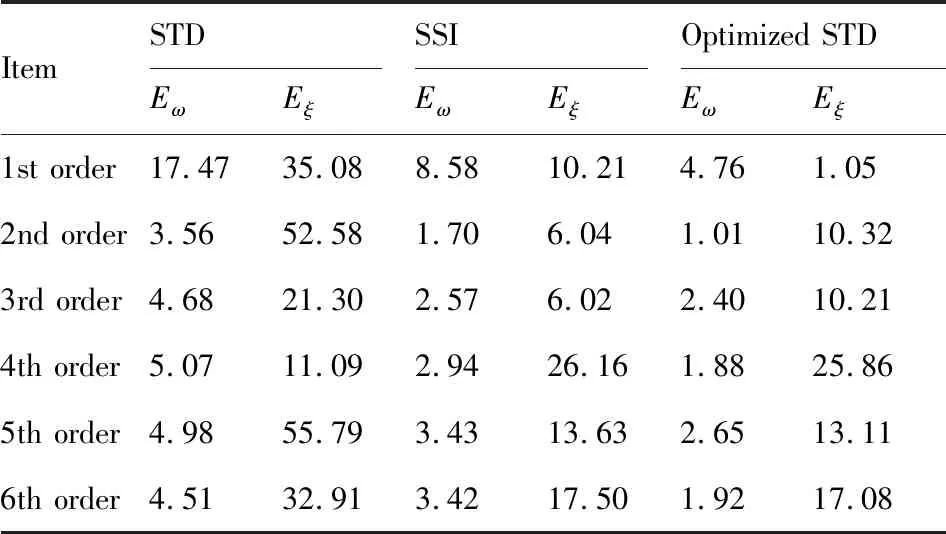
表3 STD、SSI和优化STD法模态参数识别误差
综上,该方法不仅提高了装配界面模态参数的识别精度,而且还能自动判别模态阶次,在一定程度上提高了计算效率,降低了实验成本。因此,优化STD法可比较有效地应用于垂尾装配界面模态参数的识别,以优化其精加工过程的动力学特性,从而保证装配界面的精加工质量。
值得指出的是,在外界激励形式未知的情况下,采用优化STD法能较为准确地辨识出装配界面的模态参数。因此,该方法对其他类似于装配界面的大型航空航天、汽车、船舶等领域的薄壁件加工过程的模态参数识别具有一定的适用性,可为优化其加工工艺参数及动力学特性提供一定的理论指导。
4 结 论
1) 基于STD法原理及Toeplitz矩阵并结合模态置信因子及模态保证准则,首次提出了面向垂尾装配界面精加工过程模态参数识别的优化STD法,通过切削实验及锤击测试验证了该方法的可行性和有效性。
2) 在外在激励形式未知的情况下,优化STD法通过实测振动位移数据协方差矩阵、模态置信因子及模态保证准则可消除大部分噪声信号对模态参数识别的影响,提高了优化STD法模态参数的识别精度。
3) 根据垂尾装配界面精加工过程的特点,首次将优化STD法用于其精加工过程的模态参数识别中,为装配界面精加工工艺参数选择提供了一定的理论依据,为其动力学特性的研究提供了一定的基础。
4) 建立的基于优化STD法的装配界面模态分析方法,可用于研究航空航天、汽车、船舶等领域的大型薄壁零件动力学特性分析和优化。
