风扇出口导向叶片低噪声设计Ⅰ：方法与优化

蒋永松，郑文涛，赵航，杨明绥，王咏梅

中国航发沈阳发动机研究所，沈阳 110015

随着民用涡扇发动机涵道比的不断增大，喷流速度降低，喷流噪声进一步减弱[1]，使得风扇噪声在发动机总噪声中越来越突出，无论在起飞还是降落阶段都占有较大的比重，因此，风扇的低噪声设计已成为现代大涵道比涡轮风扇发动机的研究重点[2-4]。

风扇噪声的一个最主要噪声源为转子尾迹与外涵出口导向叶片(Outlet Guide Vanes，OGV)或静子之间相互干涉所产生的噪声(转/静干涉噪声)，通过干涉过程，将转子尾迹中的涡能转换为向上游和下游传播的声能[5-6]。尽管在转/静干涉噪声中也存在宽频成分，但转子叶片通过频率(Blade Passing Frequency，BPF)及其倍频(或谐波)分量仍是干涉噪声中最突出的部分[7]。为了降低转/静干涉噪声，最直接的方法是通过合理选取转子和OGV的叶片数，使得声波满足“Cut-off”准则[8]，从而减少可传播的声模态。适当增加转子和OGV之间的距离，也可以有效降低风扇噪声，当轴向距离增大时，转子的尾迹在到达静子前缘时得到充分掺混和衰减，从而可减小OGV对尾迹的非定常响应，进而降低尾迹与OGV的干涉噪声，这对高频噪声分量的降低效果更显著，但距离的增大常常受到发动机重量和性能的限制。

实际上，OGV的轴向掠形和周向倾斜也是降低转/静干涉噪声的有效手段[9]。Kazin[10]的研究表明，静子叶片沿转子旋转方向倾斜30°，2倍BPF的纯频噪声降低了1.5～3.5 dB。Envia和Nallasamy[11]的研究进一步表明，适当运用静子叶片的掠形和倾斜布置方案，可大幅度降低转/静干涉噪声，他们还提出了降噪设计的一条基本准则，即静子叶片的叶尖相对叶根向下游掠形且叶片向转子旋转方向倾斜，可以获得较好的降噪效果。张伟光等[12]在Namba[13]的基础上采用三维升力面理论建立了可以考虑叶片弯掠组合影响的气动声学模型，探讨了掠形和倾斜对于噪声的影响机制。

尽管已经被研究者大量证实，通过OGV的轴向掠形和周向倾斜等技术能够有效控制转/静干涉噪声水平，但在目前风扇/压气机的气动设计过程中并未将声学评估作为核心环节纳入设计流程中，没有建立气动/声学一体化设计方法，导致不能在方案初始设计阶段便对这些技术的降噪效果进行快速评估，满足不了低噪声设计需求。

在风扇/压气机气动设计流程中，通常将通流与叶片造型设计作为核心环节，二者相互迭代形成叶片几何构型，然后通过二维或三维气动性能评估，得到满足设计指标的压气机可行气动方案。为了强化声学设计在大涵道比涡扇发动机设计中的作用，本文在气动设计核心环节中引入声学快速预测方法，从通流设计结果中提取参数，采用管道声学与三维升力面理论相结合的解析模型预测噪声水平，实现声学优化设计对气动设计的快速反馈，真正构建气动/声学的一体化设计方法和流程。为此，本文一方面针对某型大涵道比风扇/增压级，通过研究OGV轴向掠形和周向倾斜对转/静干涉噪声的影响，建立设计参数对风扇噪声影响的关系图谱，根据这些图谱，确定低噪声OGV的基本设计参数；另一方面，在气动/声学的一体化设计的基础上，开展基于遗传算法的优化设计，进一步达到OGV低噪声设计目的。

1 快速预测方法

本文的快速预测方法是指从气动声学原理出发建立的预测噪声产生和传播的解析方法，气动声学中这类方法通常都基于Lighthill的声类比理论[1]进行发展。在声类比理论中，气动问题与声学问题各自单独处理，在数学意义上，通过对气体动力学的基本方程进行重构便可得到声学变量的线性波动方程，方程左端描述声波的传播，右端代表气动声源，当通过测量、数值计算或其他理论建模方法获得声源项后，则可以通过声源分布与传播特征(格林函数)的卷积运算，得到声波方程的形式解。本文采用管道声学与三维升力面理论相结合方法[13-15]，建立风扇转/静干涉噪声的解析预测模型。

1.1 管道声学模型

在风扇和压气机中，转/静干涉噪声问题实际上是运动介质中固体边界的发声问题，根据广义Lighthill理论中的FW-H方程[6,16]，在观测点x及t时刻，转/静干涉噪声的声压表达式p′(x,t)可写为

(1)

式中：y为声源位置；τ为迟滞时间；s(τ)为求解问题区域v(τ)的包围面；s(y)为叶片表面；fi为叶片表面的压力载荷；T为准稳态时间；yi为观察坐标；G为运动介质波动方程在相应问题中的基本解，即Green函数。将柱坐标系应用于任意形状管道Green函数中，得到圆环管道内的Green函数表达式

(2)

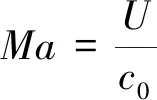
在本文的分析中，建立与文献[17]中类似的坐标系，如图1所示，则有

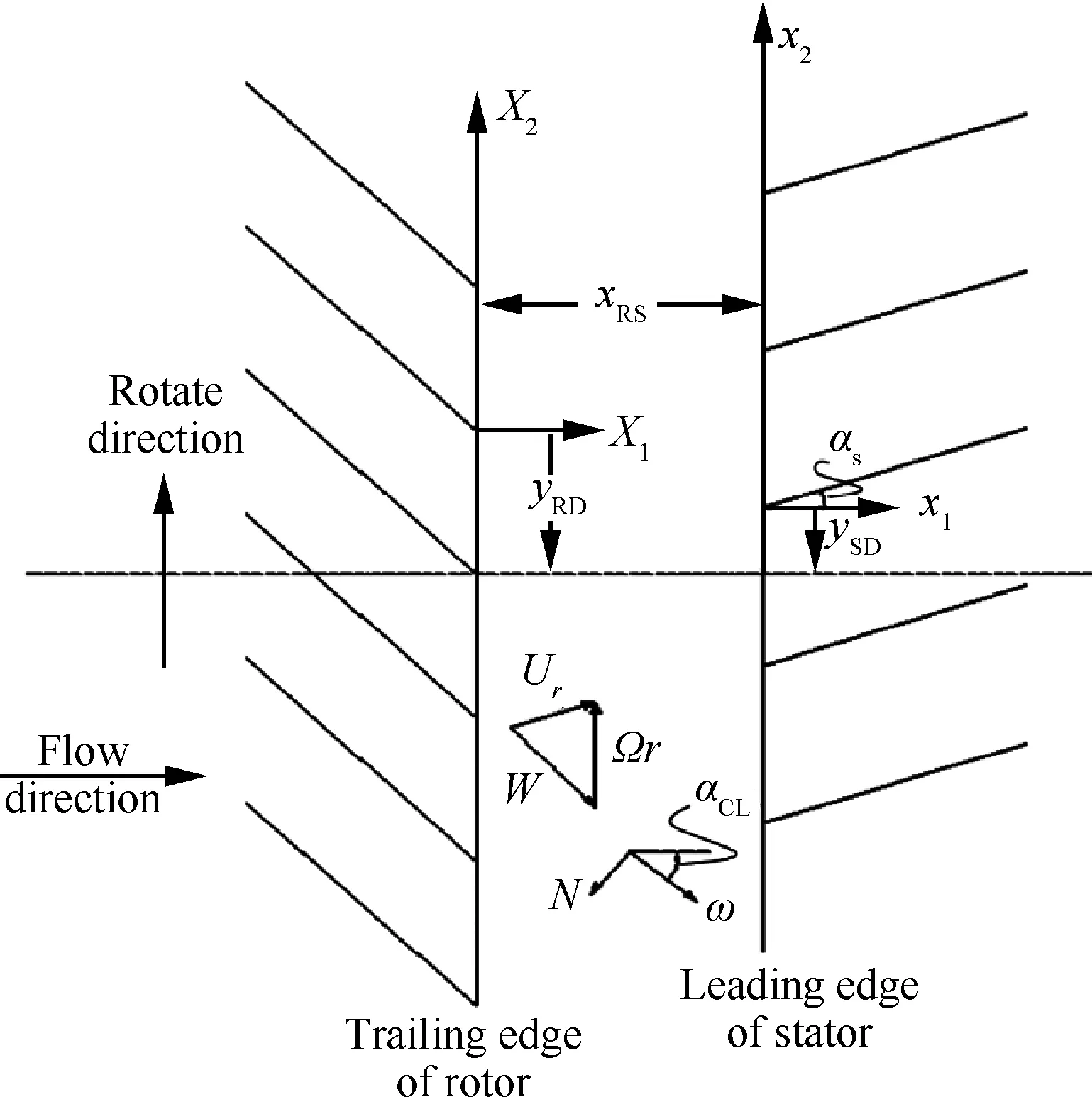
图1 转/静子在某半径处沿周向展开示意图

fi=Δpni=Δp(cosαS,sinαS)

(3)

式中：Δp为叶片表面的压力差；αS为静子与轴向夹角。这样一来，如果能求得叶片表面的载荷分布，转子和静子相互干涉产生的噪声场即可用式(1)给出。

将式(2)和式(3)代入式(1)，经过复杂的代数运算后，使用管道声模态表示的转/静干涉噪声的声场表达式为

(4)

式中：m=sB-qV,q=0,±1,±2…,V为静子叶片数;Ω为转子转频;B为转子叶片数;BΩ为转子叶片通过频率;s为谐波数，其中各谐波的模态幅值表达式为

(5)

式中：Δps为各谐波的非定常载荷；κn,m为系数。

尽管式(4)给出了声场表达式，但静子叶片上Δps仍未知，本文使用三维升力面理论方法进行求解[13]。这种方法可以考虑现代风扇/压气机中复合弯掠的复杂三维造型设计，可以评估掠形等因素对风扇噪声的影响。该方法中，将静子叶片假设为无限薄、无弯度且沿叶高方向扭曲的平板，非定常载荷分布Δps建立与上洗速度的关系，即

(6)

式中：K为积分核，表征叶栅的影响；w为来流在静子上的上洗速度，通过求解该积分方程得到Δps[13-14]，从而求得干涉声场。应该注意的是，本文中转子叶片尾缘距OGV前缘2倍转子弦长以上，OGV前缘处气流已近似轴向均匀，并且OGV安装角较小，约为15°，如图2所示。基于以上两点，认为满足三维升力面理论的基本假设。

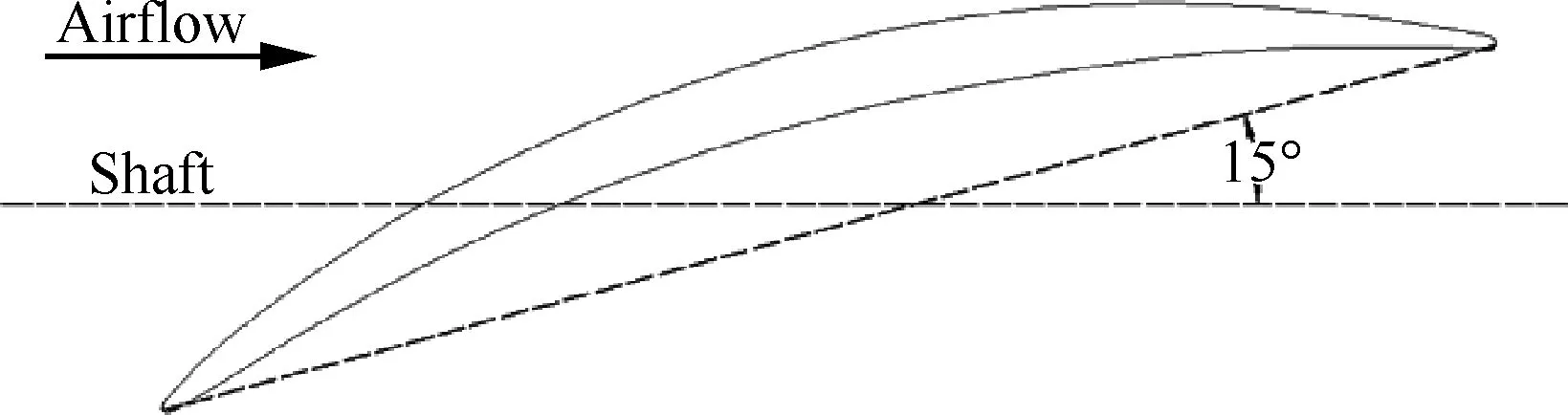
图2 OGV安装角示意图

1.2 转子尾迹模型

为了求解式(6)，本文采用Majjigi和Gliebe[18]建立的尾迹模型作为上洗速度的经验模型，Majjigi和Gliebe的研究指出，转子尾迹剖面满足高斯分布，其Fourier变换为

(7)

式中：δ为半尾迹速度宽度；wc为尾迹中心速度。δ和wc除了与风扇转子和静子的几何参数相关外，还与转子的气动参数有关，在本文的研究中，这些参数均取自于通流设计和造型设计过程。

本文只考虑转子尾迹对静子叶片的激励发声机理，在静子坐标系下看，该激励具有周期性，其频率为叶片通过频率及其谐波，因而将绝对坐标系下的尾迹速度写成傅里叶级数形式[17]，可以得到

(8)

式中：ν为静子叶片的标号；

(9)

ws=Wssin(αS+αCL)·

(10)

其中：αCL为尾迹与轴向夹角；yRD、ySD为转子尾缘、静子前缘在展开平面的y方向坐标；xRS则表示转子尾缘到静子前缘的距离，如图1所示，这些参数都是半径r的函数，下标H为叶根处对应参数。通过以上各参数，可以真实反应现代风扇/压气机周向弯曲和轴向掠形等对风扇噪声的影响。

2 气动/声学一体化设计

为了强化声学设计在大涵道比涡扇发动机风扇设计中的作用，本文在气动设计核心环节中引入声学快速预测方法评估，组成气动/声学一体化设计流程，如图3所示。特别地，目前大涵道比涡扇发动机的噪声源中，风扇与OGV之间的转/静干涉噪声占有较大比重，因此，声学快速预测方法是指第1节所讲的转/静干涉噪声解析预测方法。该方法分别以通流设计和造型设计的输出作为几何和气动参数的输入，在通流与叶片造型完成迭代设计后，便能快速开展噪声水平的评估。

由于转/静干涉噪声主要是由转子尾迹对静子非定常冲击而引起的噪声，因此，在转/静干涉噪声快速预测方法中，首先根据转子负荷，建立转子尾迹的表达式，并将其转换为静子坐标系下的上洗速度；以管道声学理论为基础，根据广义声类比理论，结合风扇/压气机声模态的特点，推导出均匀运动介质中转/静干涉噪声的声压表达式；由于转/静干涉噪声的声场表达式中，可根据叶片表面的无穿透条件，由上洗速度与其诱导的声速度建立求解非定常载荷的积分方程，完成非定常载荷的求解过程，从而得到管道内由转子尾迹与静子相互干涉产生的声场，进一步求得声压级、相位和前、后传声功率等。

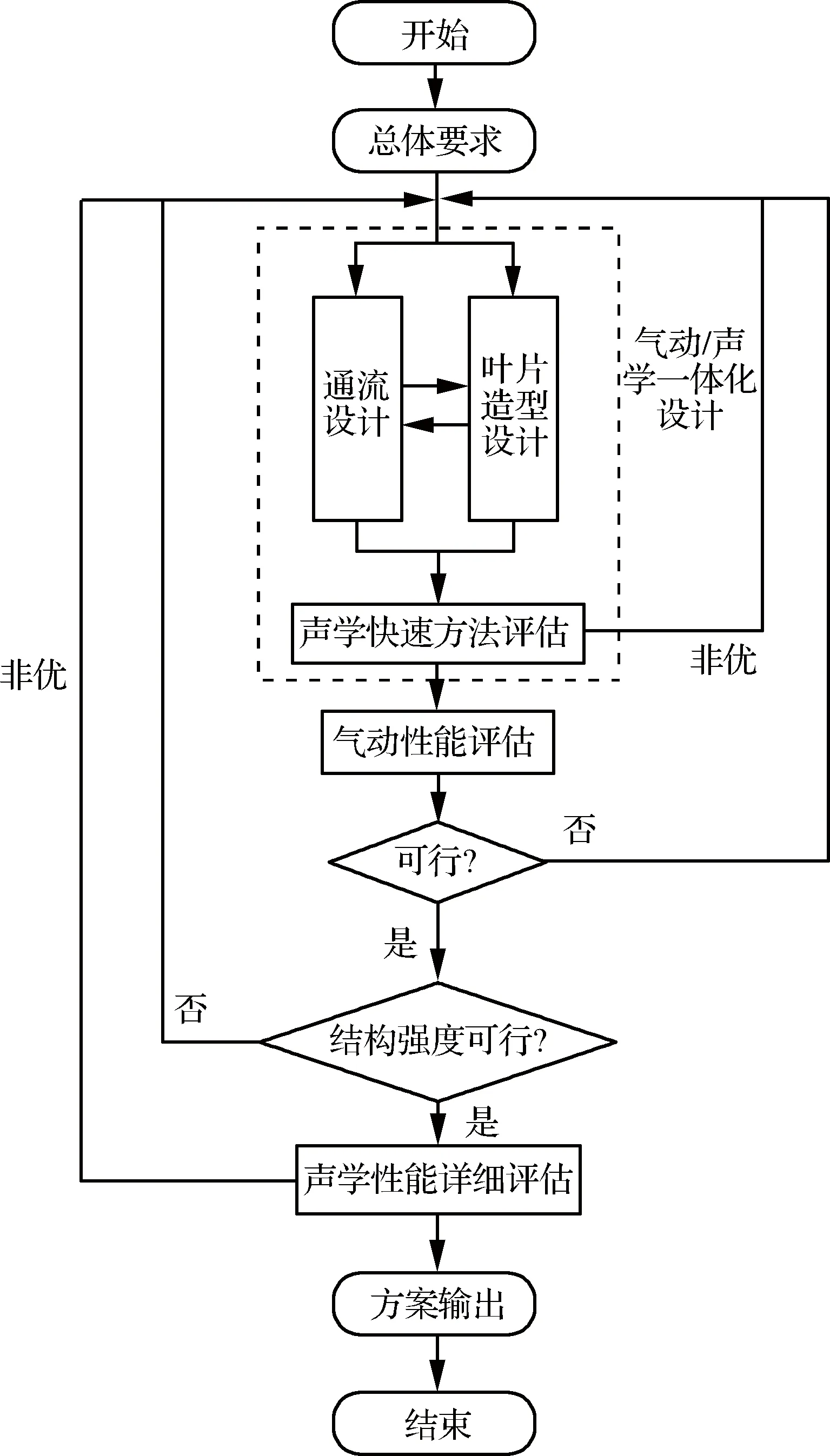
图3 气动/声学一体化设计流程

在图3所示的气动/声学一体化设计流程下，可以快速研究风扇/压气机设计中相关设计参数的变化对噪声的影响，得出变化规律，形成设计经验。当然，由于解析方法所进行的简化造成了快速预测过程不可避免的固有缺陷，在气动设计方案进行气动性能评估和结构强度可行性评估后，还需使用高精度方法进行声学更为详细的评估。

3 低噪声设计参数化

在建立了针对转/静干涉噪声的声学和气动一体化设计方法后，可以开展低噪声设计的参数化研究，以某型大涵道比涡扇发动机风扇/增压级试验件作为研究对象，系统分析OGV的轴向掠形和周向倾斜对转/静干涉噪声的影响。该试验件由风扇转子、外涵OGV和带有进口导叶的四级增压级组成，其中风扇转子叶片数为22，OGV叶片数为70。图4给出了轴向掠形角α和周向倾斜角β在文中的定义。图4(a)中，OGV的轴向掠形角α为叶尖和叶根在子午面上投影中点的连线与径向的夹角，当叶尖相对于叶根更偏向于下游时，定义掠形角为正，反之则为负。图4(b)中，OGV的周向倾斜角β为沿发动机轴线从前往后看积叠线与径向线的夹角，当OGV在周向沿风扇转子旋转方向倾斜时，定义倾斜角β为正，反之为负。

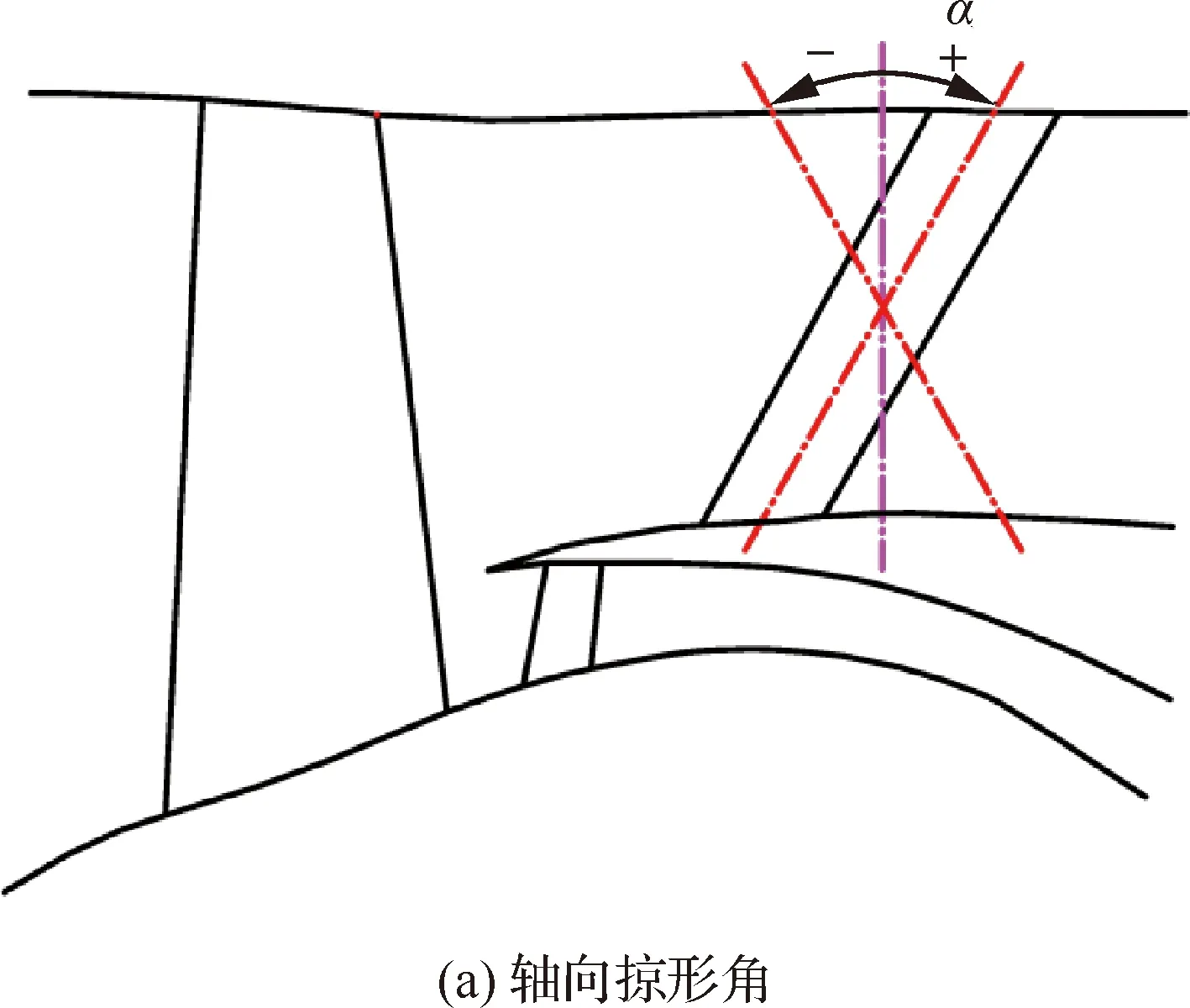
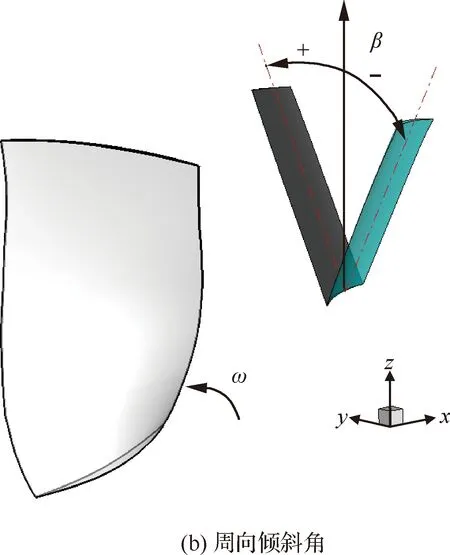
图4 轴向掠形和周向倾斜的定义

3.1 轴向掠形对风扇噪声的影响

针对掠形对转/静干涉噪声的影响，本文分别选取了-30°、-20°、-10°、0°、10°、20°和30°共7种不同OGV掠形角进行分析。在掠形的过程中，保证OGV与转子的平均距离不变。在改变掠形角时，分别以OGV叶尖和叶根的中点为基点，平移原设计对应的叶尖和叶根流路，分别形成尖部和根部流路，与此同时，周向倾角保持为0°。

由于在压气机气动设计方法中，轴向的掠形需要在通流设计过程中通过子午流面上的计算站形状进行控制，计算站的改变就需要进行通流设计与叶片造型设计的迭代设计，从而生成叶片几何，然后再由二者最终的输出作为噪声快速预测方法的输入，这也是发展气动/声学一体化设计方法的原因。

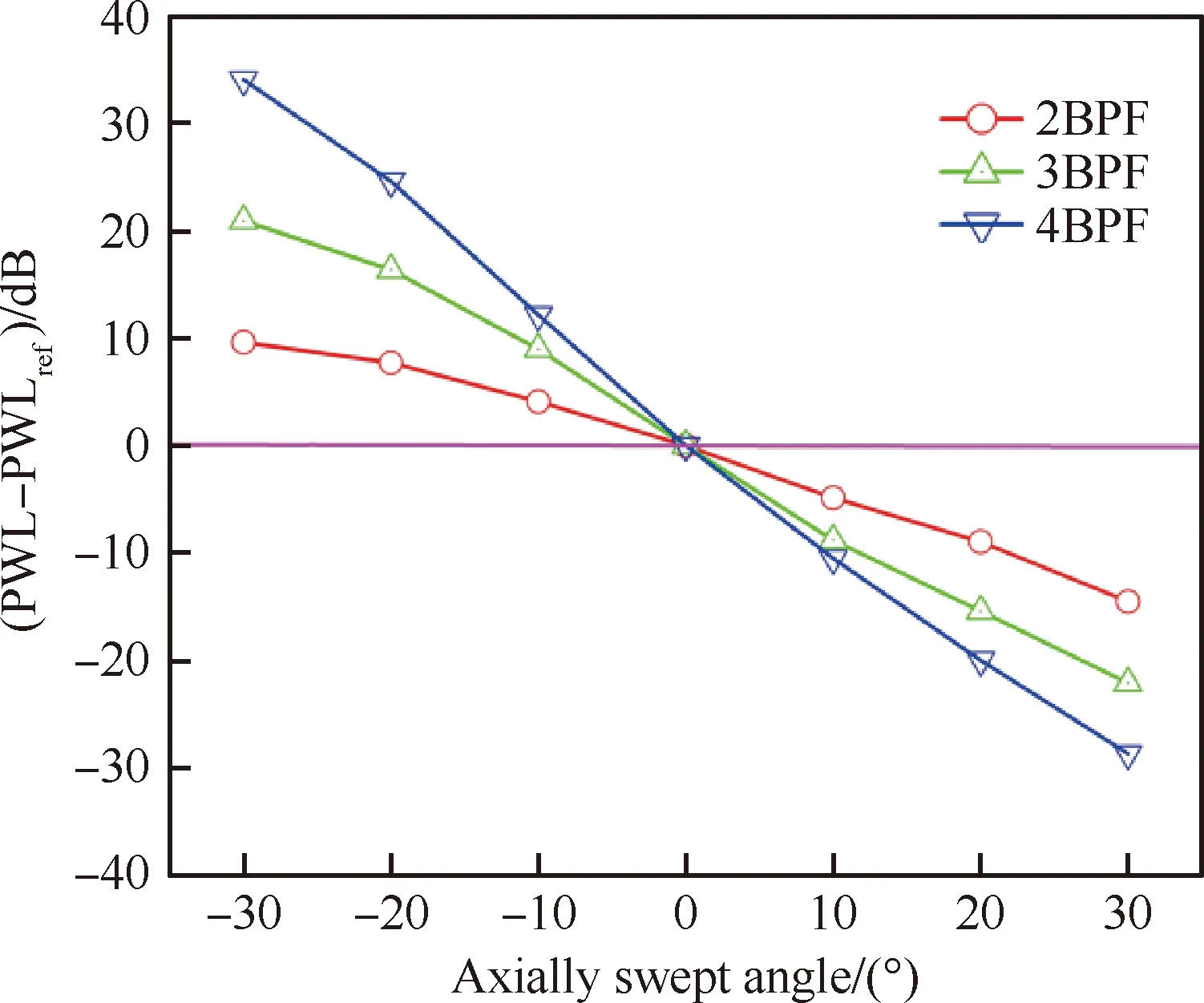
图5 轴向掠形对前传噪声的影响

图5和图6分别给出了快速预测方法获得的轴向掠形对前传和后传各阶BPF噪声声功率的影响，图中以掠形角α=0°时对应的参考声功率(Reference Sound Power Level，PWLref)作为参考基准，由声功率(PWL)相对变化量PWL-PWLref表示降噪量，该值为正时表示噪声增加，为负时表示噪声降低，由于风扇在转子和静子叶片数的选取上满足Cut-off条件，因此1阶BPF被截止。从图中可以看出，随着BPF阶数的增加，对噪声的影响也越大，负角度的掠形会造成噪声增加，正角度的掠形可以减少噪声。

总的来说，OGV掠形对转/静干涉噪声有重要影响，掠形30°能降低2阶BPF噪声10 dB左右，而且对高阶BPF的降噪效果更明显。

3.2 周向倾角对风扇噪声的影响

与研究掠形对转/静干涉噪声影响一样，分别选取-30°、-20°、-10°、0°、10°、20°和30°共7种不同OGV倾斜角进行分析，同时保证轴向掠形角为0°。但与掠形不同的是，在压气机气动设计方法中，周向的倾斜可以在保持S2通流设计不变的情况下，通过叶片造型过程中的周向积叠来完成。

图7和图8分别给出了周向倾角对前传和后传噪声的影响。可以看出，OGV的周向倾角对噪声的影响比轴向掠形小。与掠形不同的是，周向倾角对低阶BPF噪声的影响比对高阶BPF的影响大。总体来讲，当倾角为30°时，2阶BPF噪声的降噪量只有7 dB左右。

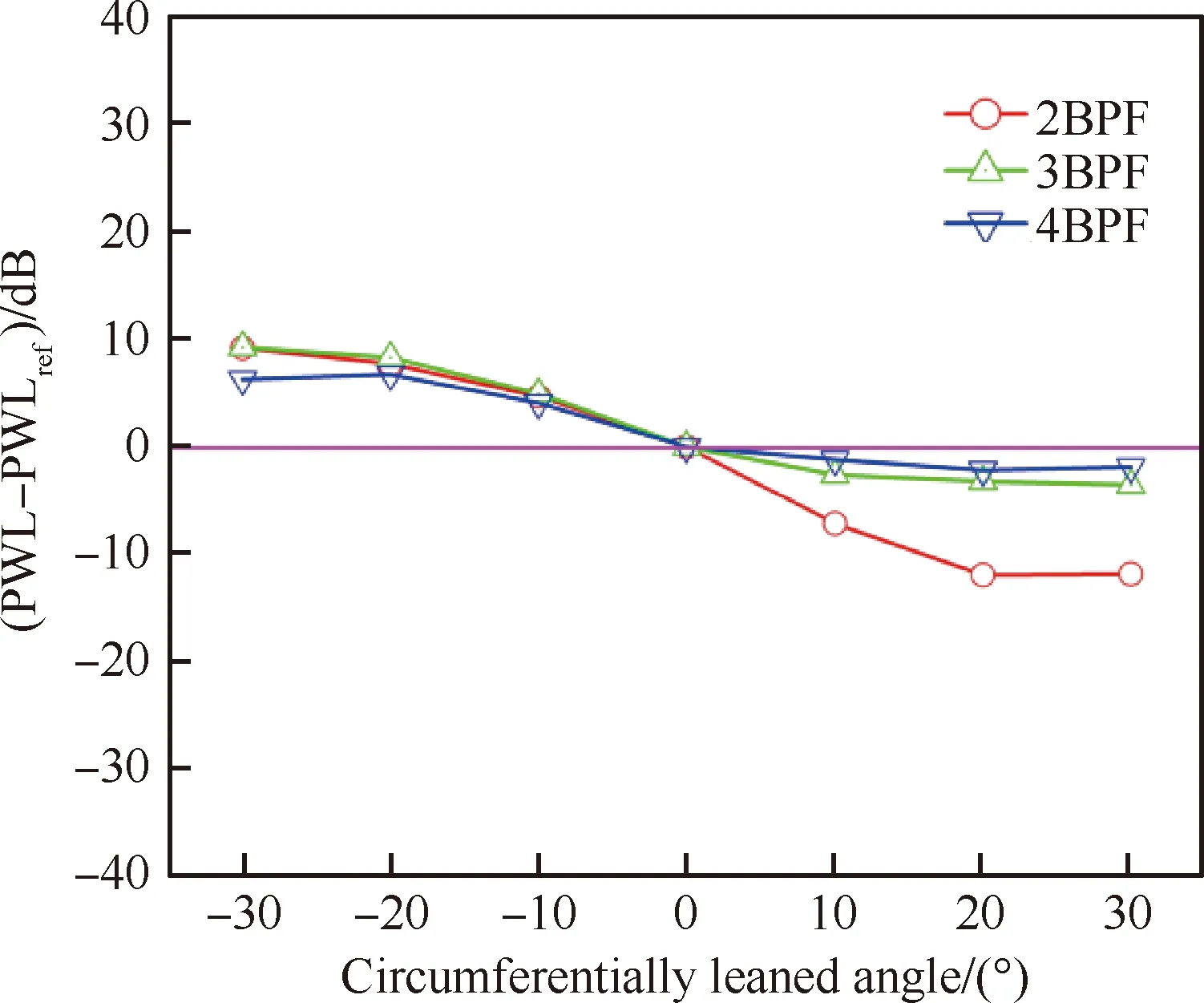
图8 周向倾角对后传噪声的影响

3.3 轴向掠形与周向倾角对噪声的组合影响

为了研究轴向掠斜与周向倾斜对噪声的组合影响，图9和图10分别给出了OGV在不同倾斜角条件下前传和后传噪声随不同掠形角的变化曲线，图11和图12分别给出了OGV在不同掠形角条件下前传和后传噪声随不同倾斜角的变化曲线。图中以原型(Original，ORI)OGV设计状态，即(α,β)=(10°,0°)，对应声功率PWLref作为参考基准。从图中可以看出，正的轴向掠形总能大幅减少噪声，噪声的减少量近似与掠形角成线性关系变化；另外，正的周向倾角能够在一定程度上强化掠形的降噪效果，当(α,β)=(30°,10°)时，2阶和3阶BPF噪声都能达到10 dB以上降噪量，当(α,β)=(20°,10°)时，2阶和3阶BPF噪声也能达到10 dB左右的降噪量，略高于掠形角α=30°。但当倾角β>10°后，OGV周向倾的强化作用几乎不再增加；负向的倾角会弱化掠形的降噪效果，在倾角β=-30°条件下，即使是α=30°的大掠形角，也不能取得任何降噪收益。

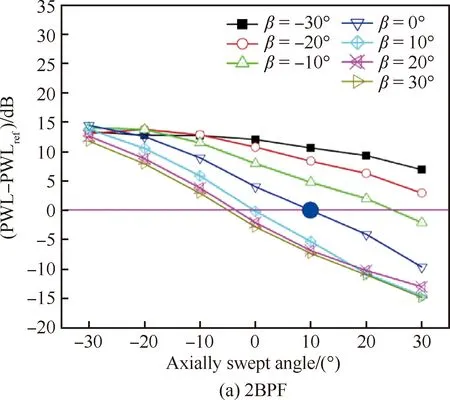
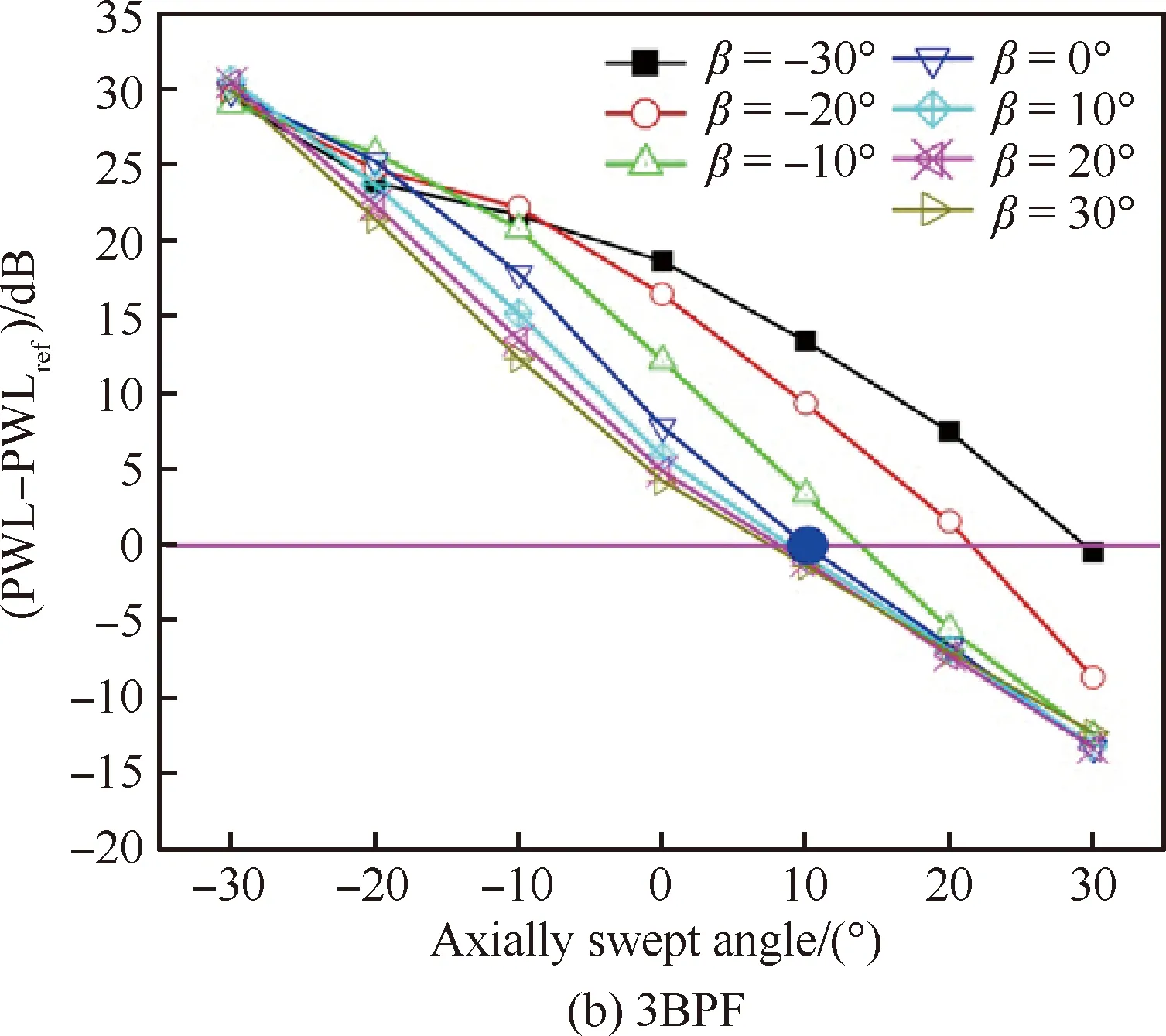
图9 不同倾角条件下轴向掠形对前传噪声的影响

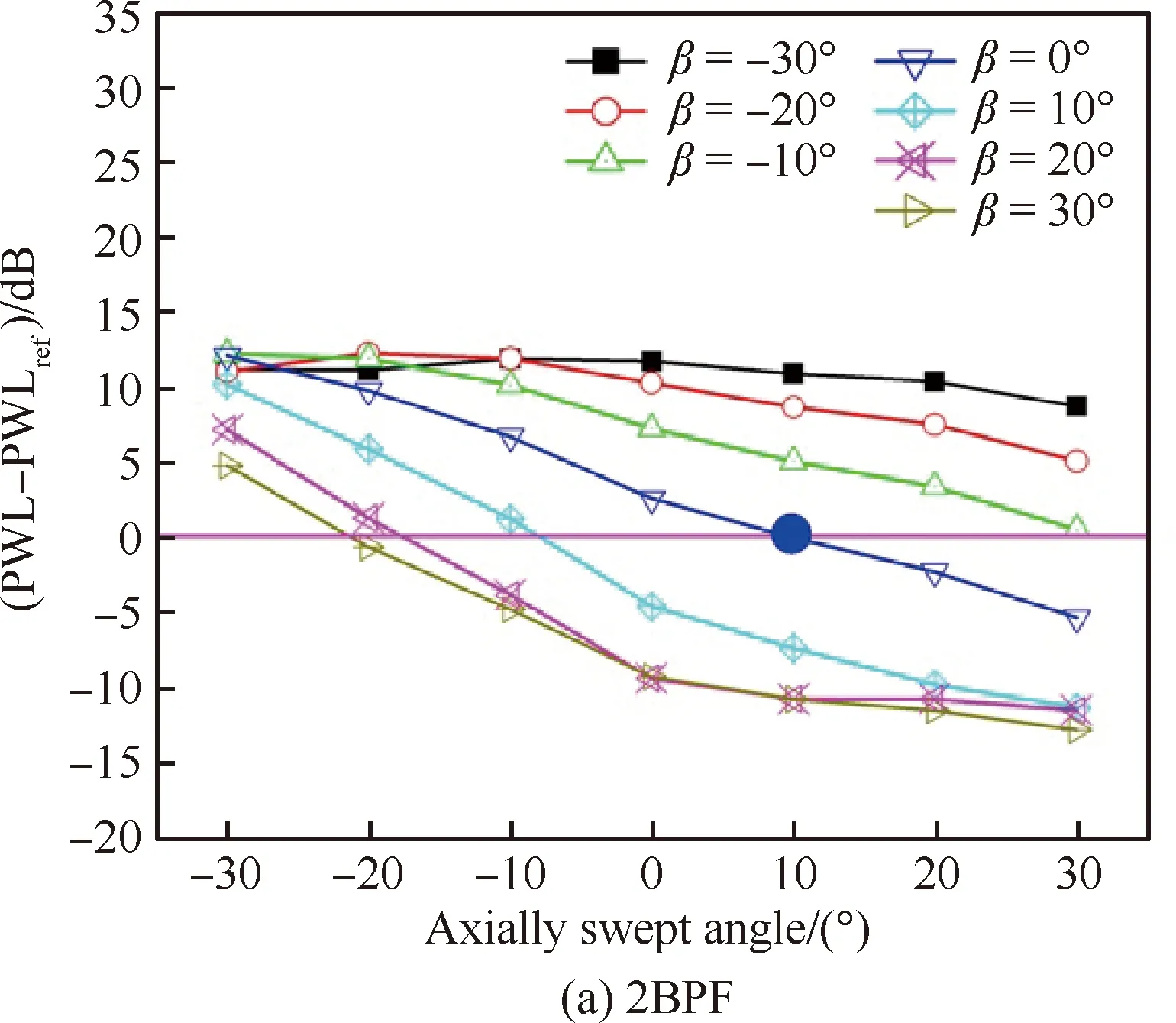
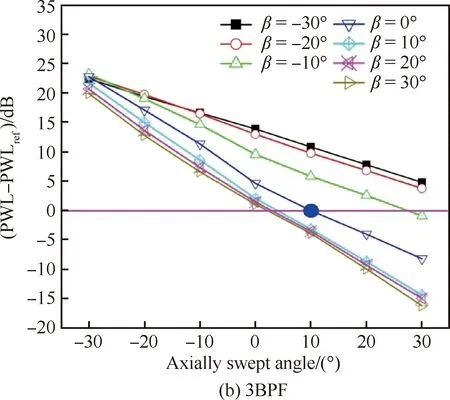
图10 不同倾角条件下轴向掠形对后传噪声的影响

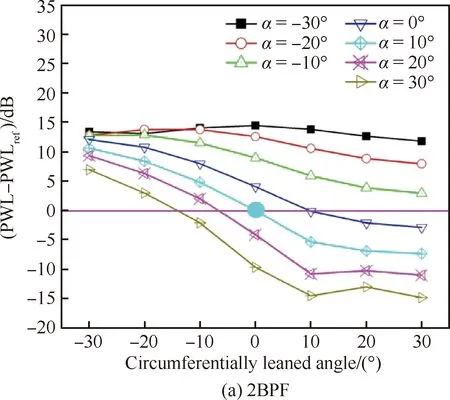
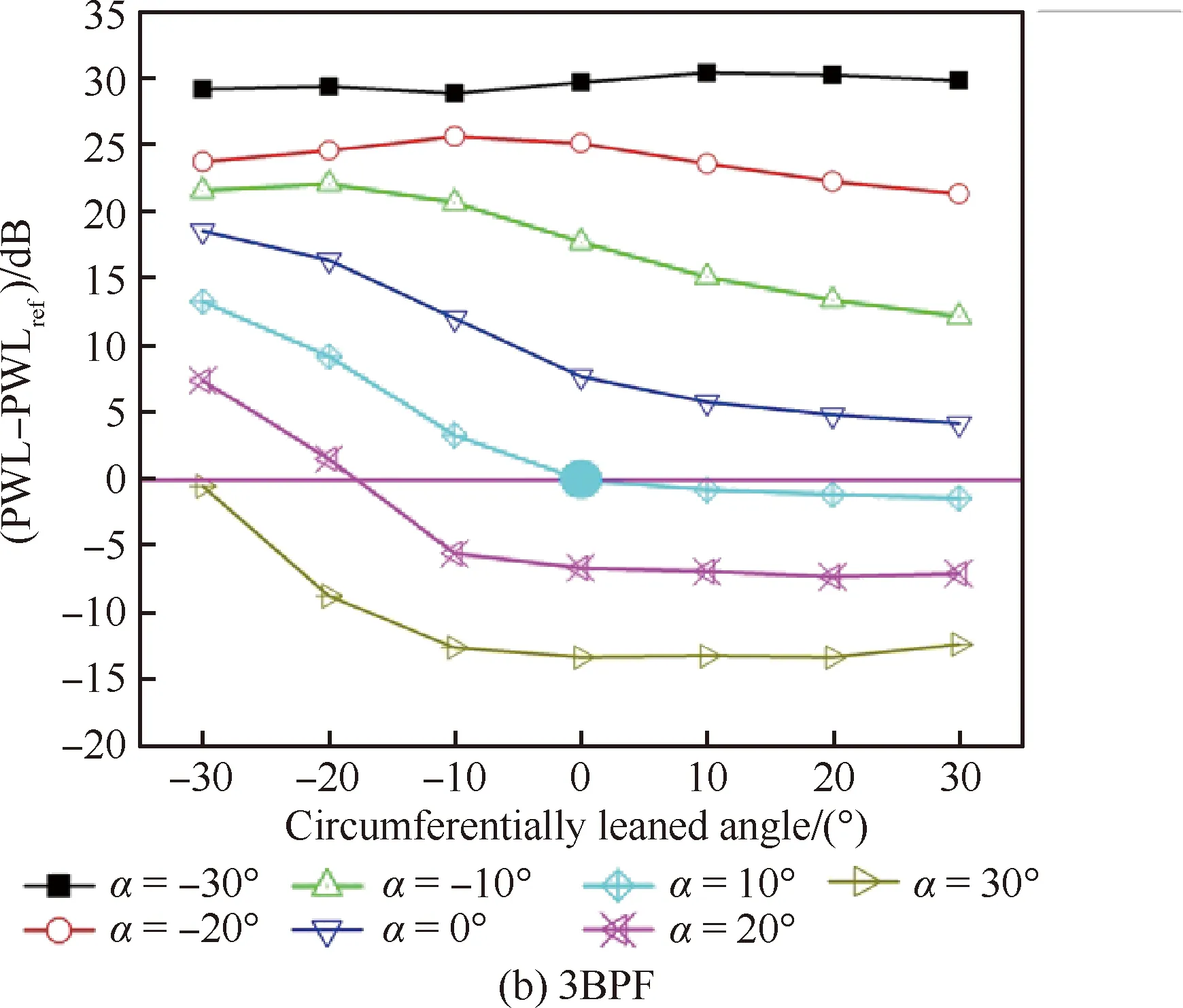
图11 不同掠形角条件下周向倾角对前传噪声的影响

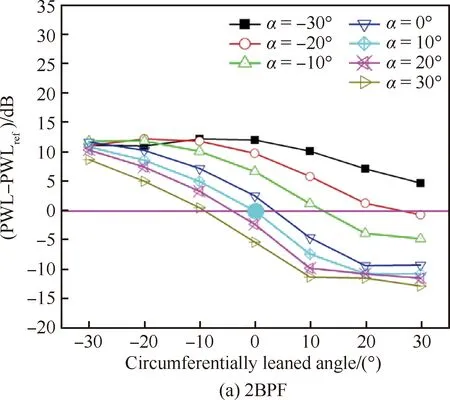
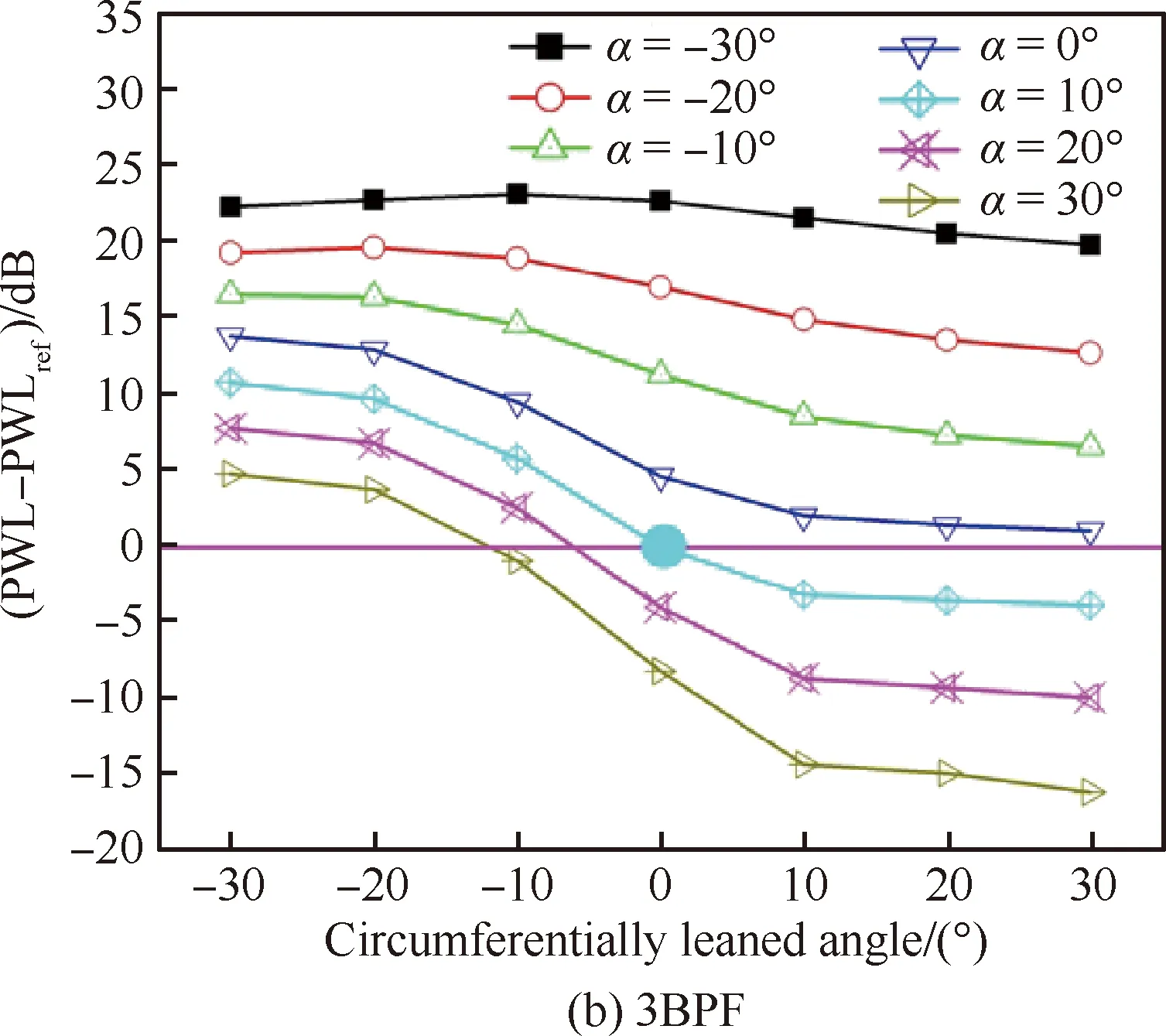
图12 不同掠形角条件下周向倾角对后传噪声的影响

4 低噪声OGV优化设计

实际上，前述的降噪效果都是在保证OGV与风扇转子的平均轴向距离不变的情况下得到的。受原风扇/增压级试验件结构限制，只能在固定叶尖子午投影位置的原则下开展低噪声OGV设计，这无疑大大增加了低噪声设计的难度，主要表现在两点：第一，固定了OGV叶尖子午投影位置，在一定程度上就固定了OGV与转子叶片间的最大距离，通过加大两者距离来降低干涉噪声的手段因此受到了限制；第二，固定了OGV叶尖子午投影位置，想要加大掠形角，就需要将OGV根部前移，这又势必导致OGV与转子叶片间的距离减小，掠形的降噪收益与距离减小导致的噪声增加形成尖锐矛盾。

为了缓解这样的矛盾，选择以OGV轴向掠形α=20°，周向倾斜β=10°为基准，采用基于遗传算法[19]的优化方法，进一步开展了低噪声OGV的优化设计，寻求通过非均匀轴向掠形[20]和周向倾斜进一步提升声学收益。优化过程中，固定OGV叶尖、根轴向位置，将叶片的前缘子午投影定义为6阶贝塞尔函数，如图13所示，叶片周向积叠轴定义为3阶贝塞尔函数，如图14所示，分别各自以控制点轴向及周向偏移量为优化变量，以降噪量为优化目标。为降低对风扇气动性能的影响，保证OGV的负荷水平不发生变化，优化过程中叶片的子午弦长保持与原方案一致。

在优化过程中，种群规模设定为16，最大遗传代数为200，杂交类型为均匀杂交，杂交率设为0.5，变异率为0.02。图15给出了使用遗传算法得到的优化结果解集，图中给出了4种不同权重的优化结果，如Eq03Eh07表示前传噪声降噪量的权重为30%和后传噪声降噪量为70%的组合，其他方案以此类推。从结果中选取相对较优的2个方案，分别命名为优化方案A(OptimizedA，OPT-A)和优化方案B(OptimizedB，OPT-B)，相对于优化基准方案(α,β)=(20°,10°)，OPT-A前传噪声与后传噪声分别降低2.2 dB和1.0 dB，OPT-B前传与后传噪声分别降低0.5 dB和1.8 dB；相对于原OGV方案，OPT-A前传噪声与后传噪声分别降低9.4 dB和8.8 dB，OPT-B前传与后传噪声分别降低8.7 dB和9.6 dB。

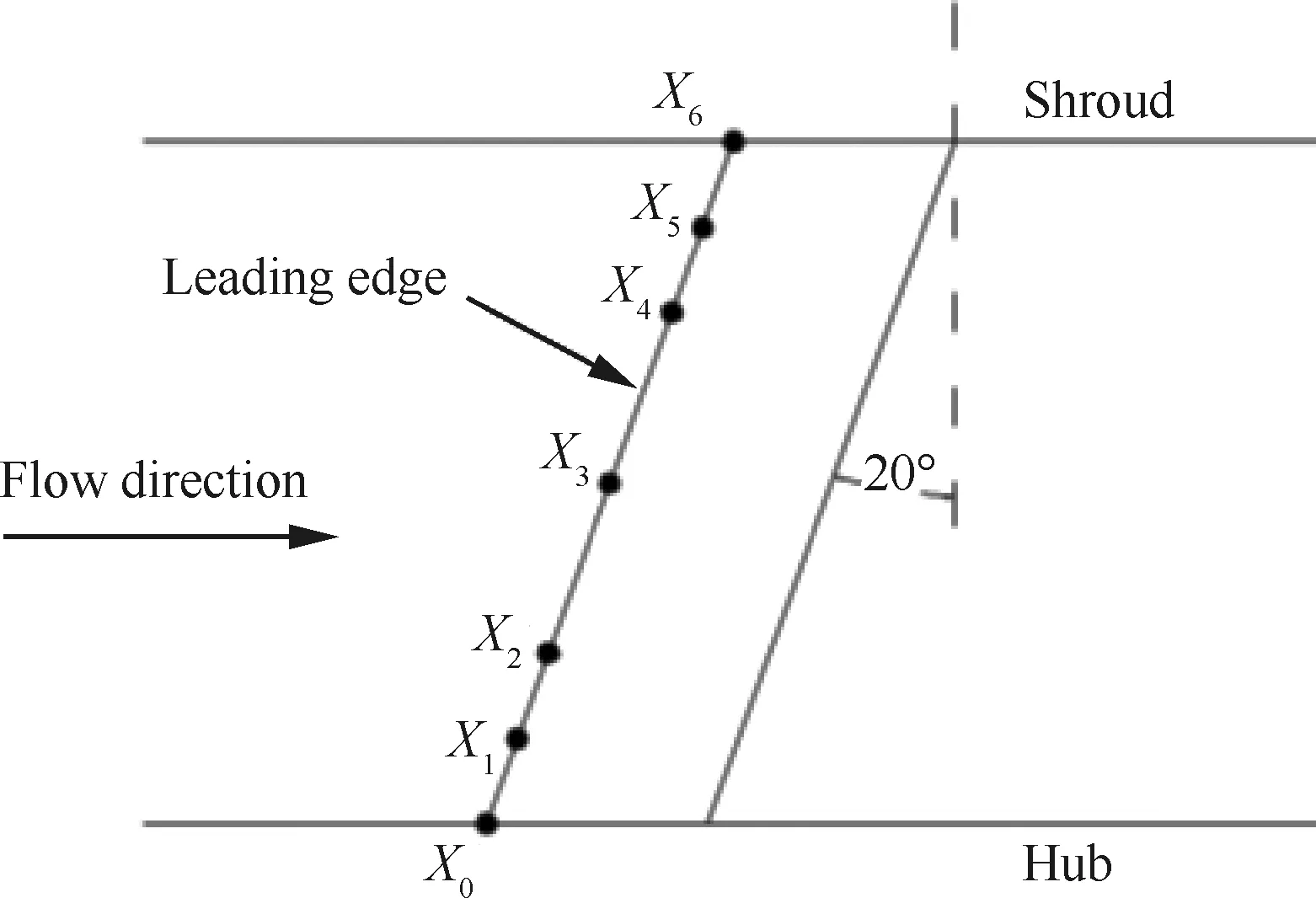
图13 OGV轴向掠形参数化示意图

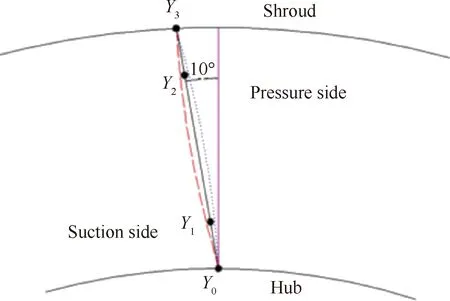
图14 OGV周向倾斜参数化示意图

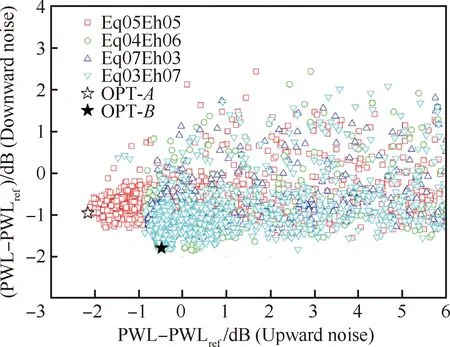
图15 基于遗传算法的优化结果

叶片子午投影如图16所示，X和R分别为轴向和径向无量纲坐标。图17和图18分别给出了经优化设计后掠形角和倾斜角沿叶高的分布，与原方案10°的掠形角相比，两优化方案沿叶高具有非常不均匀的掠形角分布，OPT-A方案的掠形角变化范围为-3°～35°，OPT-B方案的变化范围为-3°～26°，但两优化方案倾斜角之间的差异比较小，图19给出了稠度沿叶高的分布，由于在优化设计过程中保证了子午弦长不变，所以优化方案稠度变化不大，在一定程度上保证了OGV的气动性能与原方案基本一致。各方案的三维结构如图20所示，图中黑色为风扇转子及原方案的OGV，深灰色为OPT-A方案的OGV，浅灰色为OPT-B方案的OGV。

由于气动/声学一体化设计过程中使用的噪声快速预测方法对实际问题进行了大量简化和近似，如将真实的发动机管道简化为等直径环管、叶片简化为无弯度和无厚度的平板等，这些简化和近似无疑会增大预测误差，因此，针对这2个低噪声方案，将在第2篇[21]文章中开展声学性能的详细评估，并同时给出气动性能的对比。

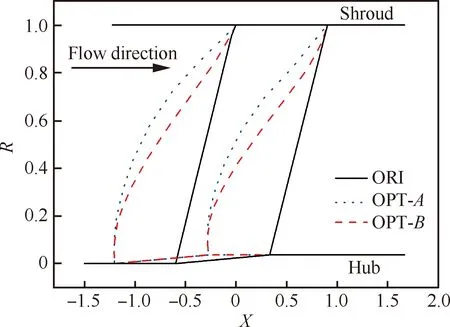
图16 OGV各方案的子午投影

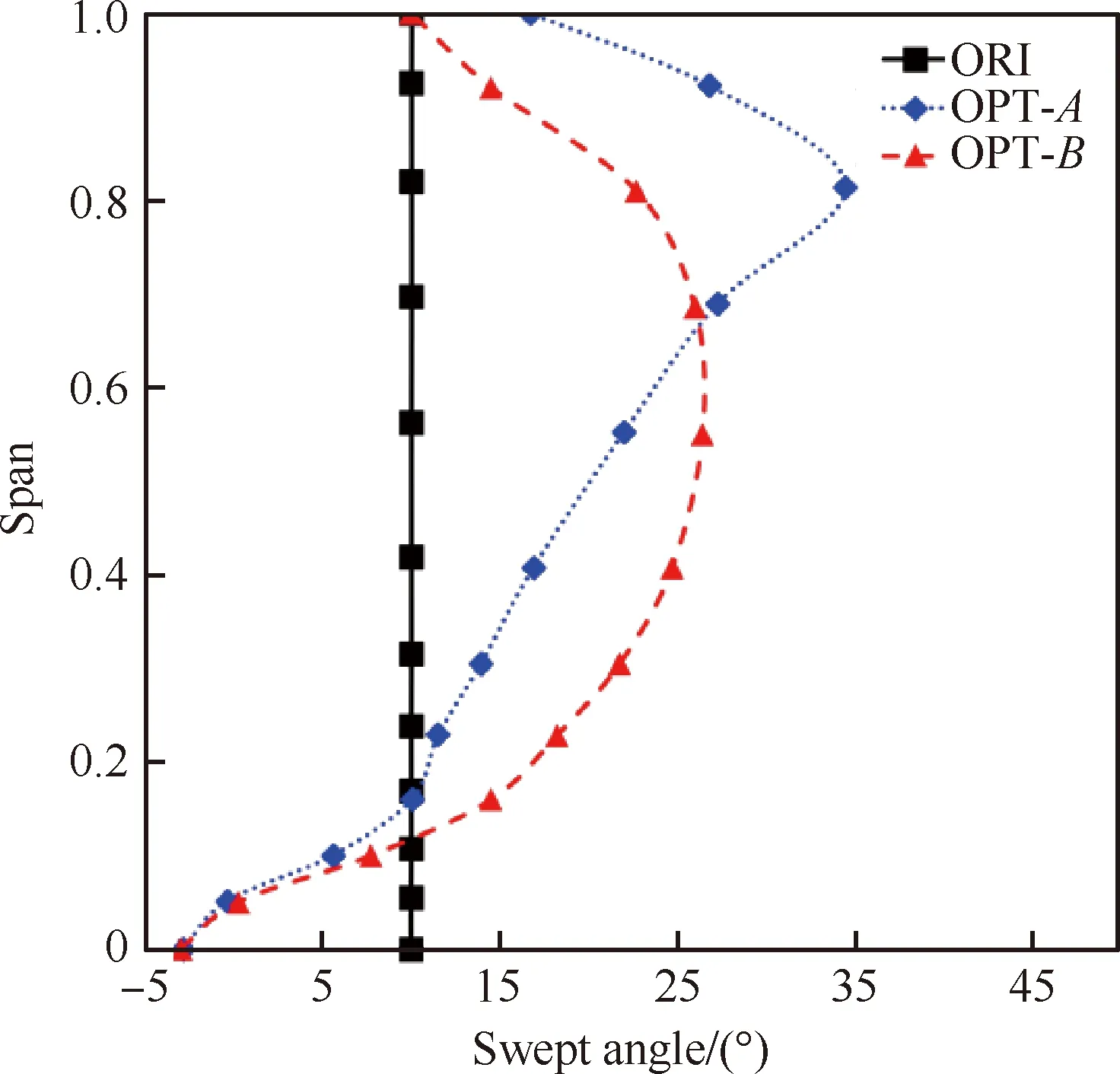
图17 掠形角沿叶高的分布

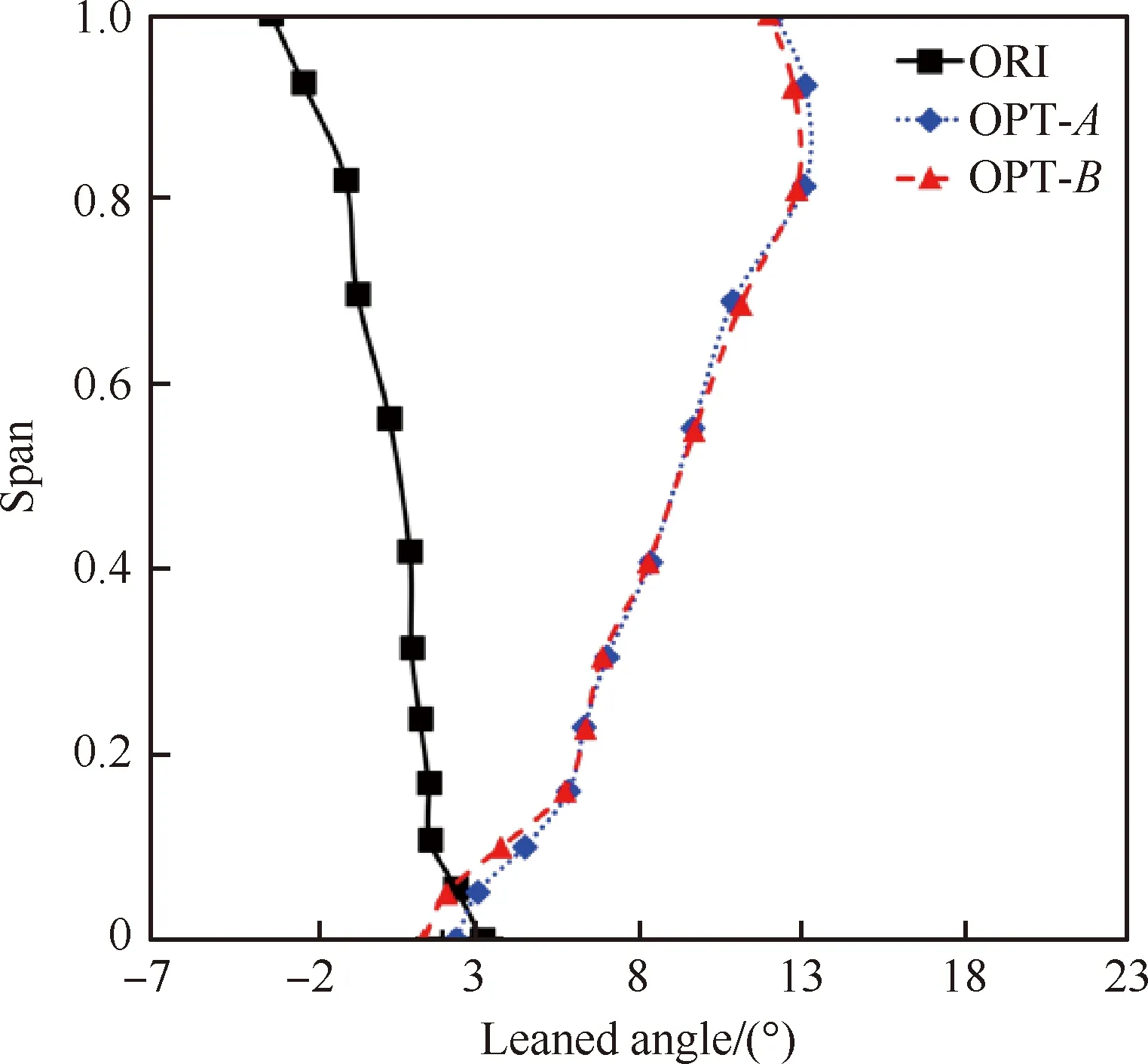
图18 倾斜角沿叶高的分布

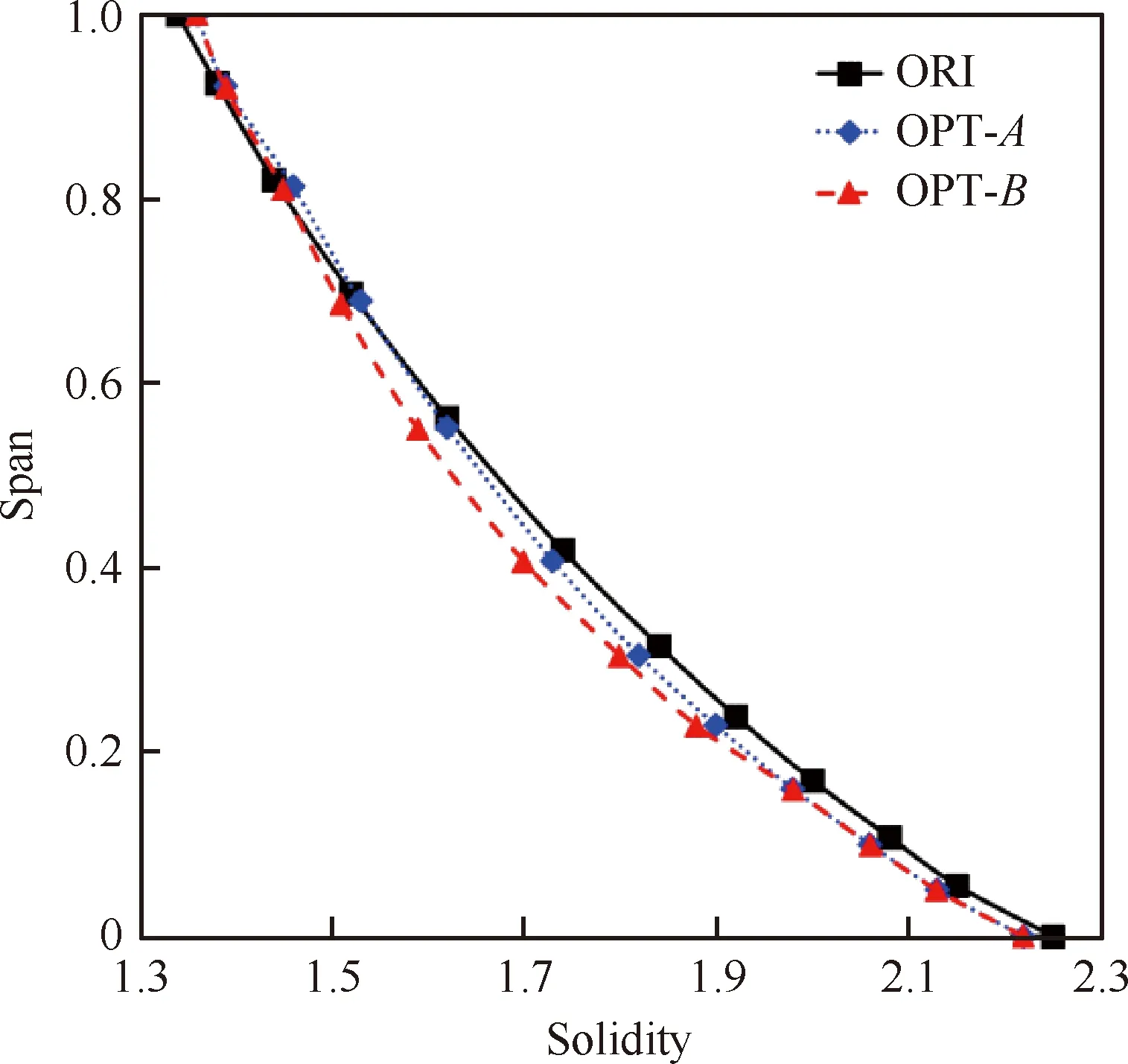
图19 稠度沿叶高的分布

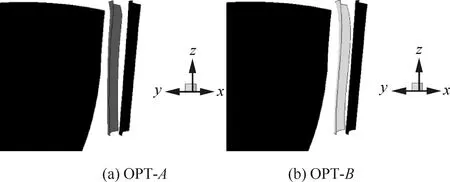
图20 OGV优化方案叶片三维构型

5 结 论

本文利用三维升力面与管道声学理论，结合尾迹模型，直接从气动设计输出提取参数，实现了噪声水平的快速评估，建立了气动/声学一体化设计方法。采用该方法，对风扇/增压级的转/静干涉噪声水平进行了快速评估，系统研究了轴向掠形角与周向倾斜角对噪声水平的影响，优选出掠形角与倾斜角的最佳组合，并以此为基础，进一步采用遗传算法对OGV开展参数化优化设计，最终获得了2个低噪声优化方案。

1) OGV掠形对转/静干涉噪声有重要影响，叶尖向远离风扇转子方向掠形能明显降低转/静干涉噪声。掠形20°～30°能降低2阶BPF噪声10 dB左右，而且对高阶BPF的降噪效果更明显。

2) 周向倾相对掠形对转/静干涉噪声的影响较小，叶尖向风扇转子旋转方向倾斜能减弱转/静干涉噪声。当倾斜30°时，对2阶BPF噪声的降噪量7 dB左右，但对高阶BPF的降噪效果并不显著。

3) 对不同掠形和不同倾斜角度的研究表明，在一定掠形角下(特别是正向掠形)，OGV倾斜10°后，继续增加倾角的降噪效果减弱，轴向掠形30°、周向倾斜10°，2阶和3阶BPF噪声都能达到10 dB以上降噪量。

4) 以轴向掠形20°、周向倾斜10°为基础，通过遗传算法获得2个低噪声OGV优化方案，经初步评估，相对于原型方案，前传与后传噪声的降噪量达到8 dB左右。