球床式高温气冷堆球流及球床辐射的理论与实验研究进展

姜胜耀，桂 南，杨星团，屠基元,2

(1.清华大学 核能与新能源技术研究院，北京 100084； 2.墨尔本皇家理工大学，墨尔本 VIC 3083，澳大利亚)

高温气冷堆满足第4代先进反应堆系统的各种要求，是21世纪美国甚至全世界最有前途的堆型[1]。我国在2006年将高温气冷堆项目列入《国家中长期科学和技术发展规划纲要(2006—2020)》，是16个国家科技重大专项之一。高温气冷堆的发展路线主要有球床式和柱状式，柱状式气冷堆主要包括美国与俄罗斯合作的GT-MHR(Gas Turbine-Modular Helium Reactor)[2-3]和日本HTTR(High Temperature Engineering Test Reactor)[4-5]等。球床式高温气冷堆主要包括美国MPBR(Modular Pebble Bed Reactor)[6]、南非PBMR(Pebble Bed Modular Reactor)[7]以及中国10 MW高温气冷堆(HTR-10)[8-10]及模块化球床高温气冷堆商用核电站示范工程(HTR-PM)[8,11]。

球床式高温气冷堆最突出的优点之一就是其固有安全性。球床式高温气冷堆的燃料元件是将全陶瓷型包覆颗粒弥散在石墨球基体中制成的，在1 600 ℃以下能保持完整性[10]。由清华大学核能与新能源技术研究院研发的HTR-10在2000年实现临界。目前HTR-PM[12]正在建设调试中，预计于2020年实现并网。

球床堆中随机密集堆积的燃料球在重力驱动下极缓慢地流过堆芯，形成了一种极缓慢的特殊颗粒流，称之为球流。球流运动特性是球床式堆芯几何设计、物理设计及核燃料循环等的基础，在球床式高温气冷堆设计改进、热工安全分析中具有基础性的地位。德国、美国、南非、中国等均积极开展了相关研究[13-15]，包括实验的和理论的，但研究尚不充分。

另一方面，堆芯球床中的热传导包括球体材料的导热、球球间接触导热、球表面的辐射传热、球与气体间的对流传热等多种传热机制，工程上可用一个综合的等效导热系数将其概括为简单的傅里叶导热[16]。因此，堆芯球床等效导热系数是综合反映球床堆传热能力的宏观参数。虽然德国研究中心安全分析和反应堆技术研究所进行了不同工况的SANA-1实验，给出了球床等效导热系数最早的实验数据，但其实验给出的球床等效导热系数温度范围在1 000 ℃以下，未能覆盖高温堆失冷失压事故工况极限温度范围(1 640 ℃)，而高温堆堆芯局部温度可达1 600 ℃，高温下颗粒间的辐射换热主导着整个球床传热，该温度范围内的数据恰是最需要的[17]。南非西北大学和M-Tech公司联合为PBMR项目建立了用于研究堆芯球床内的热传导及流体流动现象的球床导热实验装置(HTTU)，但1 200 ℃以上时，实验曲线向下掉，失真度较高[18]。因此，鉴于堆芯球床等效导热系数是直接影响高温气冷堆燃料最高温度和堆芯温度分布的关键参数，在余热导出过程中起主导作用，开展球床等效导热系数的实验研究对于反应堆分析程序的完善、研究提高高温气冷堆单堆功率的可能性以及工程的安全分析具有重要意义[16]。

本文对近年来的球流研究进行总结，同时给出下一阶段球流研究的方向。

1 实验研究

1.1 球流实验

1) 唯象实验研究

为更好地掌握球流运动特征，根据球床式高温气冷堆堆芯几何设计，建造了缩比的球流实验装置[19-21](图1a)。球流唯象实验分析成功获得了球停留时间、滞留区及滞留特性[22]、球流流线及球流纺(在获得足够多颗粒运动轨迹信息的基础上得到约95%轨迹线所包络的区域称为球流纺)、双区堆芯及球交混及扩散特性[23]的定性规律，并给后续的定量分析、机理研究和模拟对比验证提供了基础数据。基于球流唯象实验，提出了标志球法[24]来分析球流流场，标志球法是通过直接测量标志球(彩色球)在特定时刻的空间位置获得其运动轨迹，在获得大量标志球(图1b中id0～id8)的运动轨迹的基础上得到球的坐标和时间信息并计算得到球床内颗粒球流动的定量结果(图1b)。

2) 定量化实验研究

首先发展了二维球流运动界面分析法(SAM)[25]，在控制加球和卸球方式的工况下达到稳定分区球流态(即卸球中不同颜色球所占的比例与加球中相应颜色球占比相同；均值流线的曲面的球流通量处处为0，通过均值线面的瞬时球流通量一段时间内累积为0)。达到稳定分区时，可得到不同加球比例下的均值流线，并可进一步计算不同高度处的中心区宽度，给出得到的平均速度的分布等。

图1 球流实验装置(a)和标志球法得到的球流流线(b)Fig.1 Pebble flow setup (a) and measured pebble streamlines (b)

灰点表示单颗粒速度，绿点代表局部平均速度，R=0处显示该处的标准差图3 不同高度处的VyFig.3 Vertical velocity Vy on different heights

进而对球流进行了颗粒速度测量学(PTV)分析[26]，采用了动态灰度阈值方法(DTB)和新型匹配几率法(RM法)，并经颗粒识别方法检验[27]。实验用黑色玻璃球，循环球速率为150 min-1，每秒卸球的个数约占总装球量的0.003 5%，按平均值计算颗粒球每秒移动的位移小于球直径的0.01倍。利用高速摄影仪进行连续拍照，对图片进行预处理、颗粒识别、颗粒匹配及数据分析，如图2所示。各工况重复实验3～5次用于检验实验的可重复性，以保证统计可靠性。

通过PTV技术对球速度定量分析，可得不同高度条件下平均垂直速度的水平方向定量分布(图3)。图3中，Vy为垂直方向的颗粒速度，R为径向坐标(以颗粒直径d为单位)，h为数据提取点所在高度。局部平均速度通过灰色散点表示并呈现高斯分布特征。

图2 实验用颗粒球(a)、颗粒球位置标记(b) 及颗粒球轨迹(c)Fig.2 Experimental images of particles (a),particles marked by red crosses (b) and trajectories of particles (c)

基于PTV实验数据获得的球床内的极缓慢稠密颗粒流动信息，采用自相关时间τc和间歇性指数C两种特征参数在不同均值流线上的分布，可研究不同流线上的球流速度相关性、间歇性，进而对球床分区进行分析。如球床上部不同流线间自相关性较高，说明流动的协调性较高，体现整体流特征，颗粒随机运动及横向扩散小。随着高度的下降，球流随机性增强，横向扩散增强，τc也逐渐减小，两者关系呈现幂律分布τc～Hα(H为高度，α为整体流水平指数)，该规律尚需进一步研究。在径向方向上，越靠近侧壁，球流受壁面影响协调性增强，自相关性增强[25]。引入流动均匀性指数(σ)和α，通过单个颗粒球速度矢量与球床流场合速度矢量方向夹角的统计分布衡量流场运动一致性水平。

同时，基于PTV数据对球床内的搭桥现象进行了分析，发现搭桥概率分布函数在半对数坐标系下，呈现二阶多项式分布特性，在近壁区，搭桥颗粒呈现较为规则的堆积结构，而在中心区，搭桥颗粒排列取向的交错性较强。搭桥颗粒球的连续相邻颗粒球的夹角的概率分布函数表征了搭桥的稳定性。通过互相关函数方法，证明了搭桥崩塌和颗粒空间拓扑结构变化存在一定相关性。通过计算球床内典型窗口区域内的搭桥颗粒平均速度与窗口平均速度的互相关函数，发现搭桥颗粒速度和窗口平均速度呈现较高的相关性。搭桥持续特征时间和速度自相关时间呈现正相关特征。搭桥动力学特征应是球床内速度脉动的主要原因[28]。

1.2 球床等效导热系数实验

清华大学HTR-PM三维堆芯球床等效导热系数测量实验(TS-HTTF)分两个阶段实施。第1阶段是建立一个比例缩小的前期结构验证和材料筛选试验装置，构建一个模拟高温气冷堆温度的环境，测试温度要求达到1 600 ℃，具有与高温气冷堆相同性质的气体氛围，进行加热材料、测温元件材料和保温材料的筛选，以及加热元件结构、炉膛密封结构、水冷结构和绝缘结构等关键结构的验证[29]。第2阶段是建立HTR-PM三维堆芯全尺寸球床等效导热系数实验系统[28]。该装置直径5 m，床高7 m，内部含70 000个随机堆积的石墨球，分布于内径1.2 m、外径4.2 m、高度1 m的环形区域中，并保持20 Pa压力。布置90个热电偶，其中周向5个(C1～C5)，高度方向3个，径向6个(T1～T6)。目前完成了真空条件下静态填充球床内最高达1 200 ℃的瞬态法等效导热系数测试，并与南非的HTTU数据进行了比较[29-30]。图4示出了球床等效导热系数实验台测点布置、瞬态床温变化及等效导热系数对比。通过真空工况下纯堆积造成的球床等效导热系数与有冷却剂存在的情况下球床等效导热系数的比较，可深入分析球床等效导热系数的关键影响因素。按照实验计划，还将进一步开展氦气和氮气氛围下1 200 ℃和1 600 ℃的球床等效导热系数实验测试。

2 理论与数值研究

2.1 球流模型及模拟

1) 球流纺及横向扩散

借助于球流实验及离散元数值模拟，研究了球床内球流纺结构及球流纺内的横向扩散分布函数[31]。实验和计算均发现球流纺分布区域较窄，球床本体部分几乎与球流纺相互平行，在基底收缩向泄流口(图5a)。对球流纺的统计分析发现内部球的横向分布呈现近高斯分布。由于球床内为极缓慢的球流，采用准静态分析发现球流的概率分布结构为杨辉三角结构(图5b)，沿高度方向向下，其高概率区间(95%)分布于非常窄的带形区域内，即球流纺。由于杨辉三角横向分布为二项分布，其渐进分布为高斯分布，因而解释了球流纺内的径向扩散为近高斯形式。

图4 球床等效导热系数实验台测点布置(a)、瞬态床温变化(b)及等效导热系数对比(c)Fig.4 Schematic of vertical cut through test facility and thermocouples distribution among whole pebble bed (a),average temperature of five sets in middle level in whole test period (b), and comparison between three effective thermal conductivities derived by inverse method and steady-state method (c)

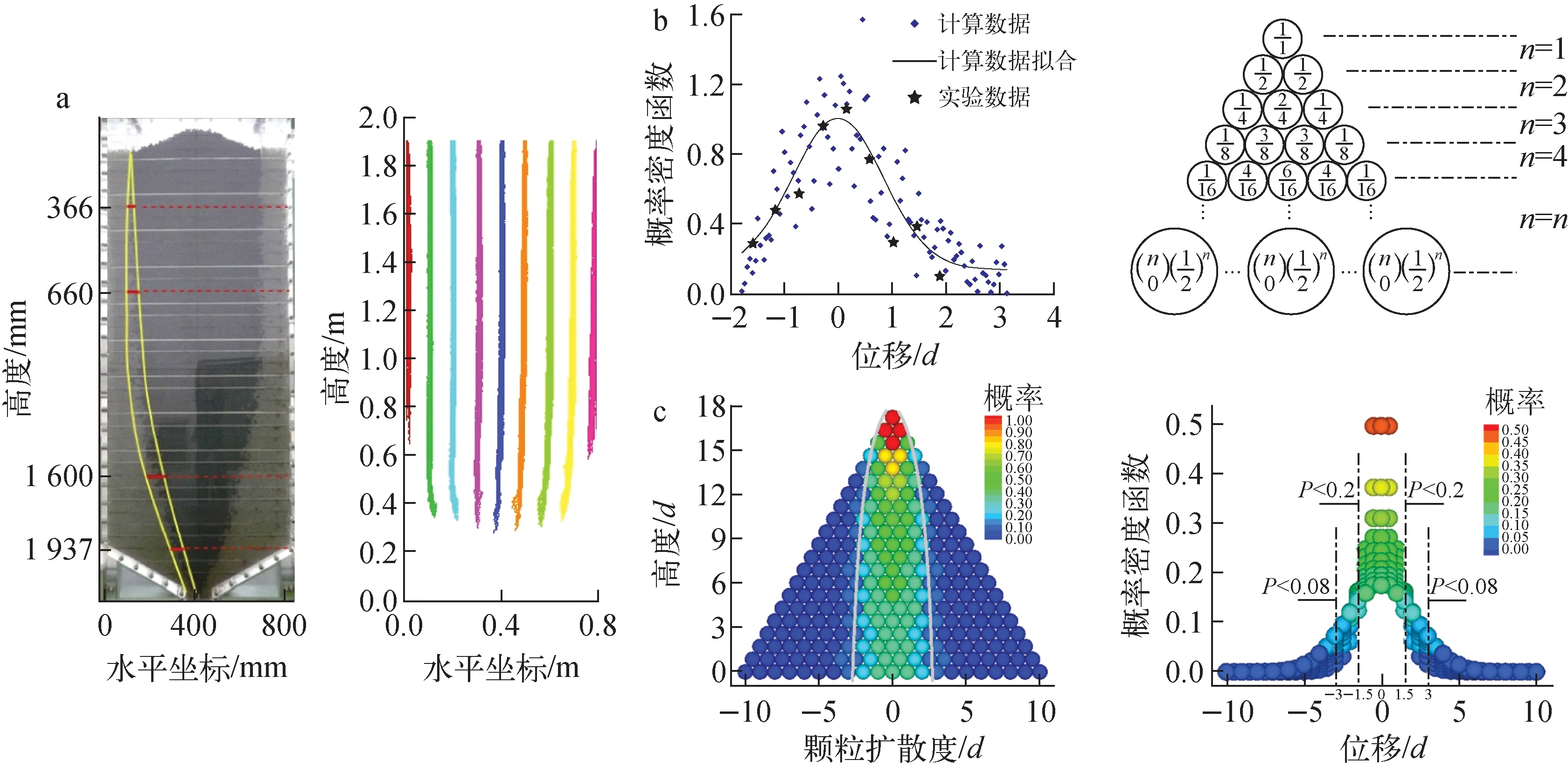
图5 实验和计算中的球流纺(a)、球流纺内的径向概率分布 及杨辉三角分布(b)以及高概率区间(95%)的正视和侧视图(c)Fig.5 Experimental snapshots of particles in granular bed and particle trajectories originated from nine fixed points at bed top (a), comparison of normalized PDFs between numerical and experimental results and probability distribution of diffusion process on all levels and positions (b), and ideal diffusion process on the first 20 levels (colored by probability on each level) and the probability view of ideal diffusion process (c)

2) 球流均匀性、滞留区(率)及床几何构型优化

为减小滞留区并分析球床基底结构对球流均匀度和滞留区的影响，分析了给定基底高度和出口直径的情况下，过渡曲线为圆心在斜面中垂线上的{Rn，n=1,2,3}圆弧曲线基底的球床及与直线母线圆锥{Rn，n=∞}和最速降线形状的比较(图6a)[32]。发现在给定循环球数下，最速降线内的球流分布最均匀，每个球的循环概率最集中，滞留率最小(图6b)。而从流型上看，球流几乎不存在滞留区(图6c)。仅次于最速降线的是R2构型。目前采用的直线母线的圆锥构型较R2构型更差一些，说明在加工条件和成本允许的情况下应尽量采用最速降线构型或R2构型。

进一步分析可发现，当采用更大的底面倾角时，如采用60°倾角替代目前的30°倾角，即使采用直线母线圆锥构型，整个滞留区亦将消失[33]。但60°倾角带来的问题是球床底部泄流口的受力要重新校核。

此外，对球床内施加内锥结构进行导流也可对床内流型进行调制，内锥应分布于基底内不超过基底高度且接近泄流口的位置[34]。但内锥的存在需要支撑，而支撑可能会对流型施加不利影响，因此还需进一步研究。

球床优化目前已采用的手段包括用近壁防结晶凹槽防止出现球流结晶。对三角、半圆及梯形结构凹槽的分析和比较可发现，有凹槽结构相对于光滑无凹槽结构能避免近壁球堆积结晶的形成，而三角凹槽在1d(d为球径)深度和1.67d间距的布置下相对于其他形状的凹槽的防结晶效果最好[35]。

3) 物性参数对球流影响

数值模拟可分析球-球摩擦与球-壁摩擦(图7)，以及不同部位的球-壁摩擦系数对球流流型和流动性的影响。

研究中采用不同的流场评价指标来定量地描述球流流场，包括整体流指数、滞留率、垂直标准差和平均次序值[36]，分别反映了球流流场的滞留现象、流动的径向均匀性和流动次序性。利用定量评价指标，可评判不同摩擦系数组合下球流流场各方面的表现。例如，整体流中所有颗粒物料处于一致的运动中，并以均匀的速度向下流动，颗粒流动服从“先进先出”序列，上下层颗粒具备较好的流动次序，各颗粒在流场中经历的时间相当，这点在球床堆中尤其重要，可保证燃料球燃耗均匀，与反应堆安全性、经济性直接相关。相比之下，漏斗流的流场径向差异大，中心区流动明显快于近壁区，近壁区颗粒流速慢，易滞留。整体流指数(Mass Flow Index, MFI)定义为流场中同高度的贴壁速度与中心速度的比值，当该值大于0.3时，流型被视为整体流，反之，该值小于0.3时，定性为漏斗流。

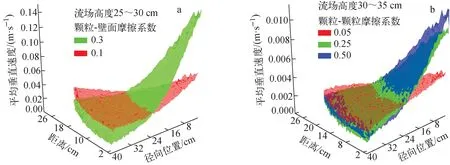
图7 球-壁摩擦(a)及球-球摩擦(b)对球流型的影响Fig.7 Cross-sectional distribution of vertical velocity with different particle-wall (a) and particle-particle (b) friction coefficients

比较发现(图8)，减小球-壁摩擦和球-球摩擦均可改善球流流场的均匀性，而球-壁摩擦是决定流型的主要因素。摩擦效应变化与流型改变之间的关系是非线性的。随着壁面摩擦逐渐减小，流型会在一段摩擦系数(μ)的区间内集中完成由非均匀漏斗流向均匀整体流的转变。所以，通过确定该流型转变区的区间，并将壁面摩擦系数控制在转变区下限以下，即可维持球床内为均匀流场。通过比较球床不同部位的壁面摩擦对整体流场的影响贡献，证实基底部分的摩擦影响明显大于本体部分，建议工程设计上应优先考虑降低球床基底部分的壁面摩擦，而在工程施工中应尽量避免基底斜坡的凹凸，或提高基底斜面的光滑性。

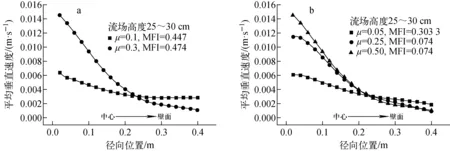
图8 球-壁摩擦(a)及球-球摩擦(b)对球流速度的影响Fig.8 Radial distribution of vertical velocity with different particle-wall (a) and particle-particle (b) friction coefficients

4) 极缓慢流态

颗粒流理论方面的研究比较滞后，颗粒流流态的定义和划分仍是模糊和粗糙的。比较受认可的理论是Campbell 20世纪90年代提出的依据颗粒间是否明显存在接触力链的分类方法[37]：能形成稳定接触力链的是弹性流，无明显力链的为惯性流。弹性流一般是稠密流，又被细分为弹性-准静态流(接触应力与剪切速率无关)和弹性-惯性流(接触应力与剪切速率呈正比)。惯性流较稀疏，颗粒间为瞬间的碰撞行为，难以形成稳定力链。根据碰撞是否为严格的两体碰撞，惯性流又被细分为惯性-碰撞流(严格两体碰撞)和惯性-非碰撞流(非严格两体碰撞)。

极缓慢流体的流态极为特殊，可从不同角度对球流流态进行分类。鉴于球流内存在间歇性瞬时速度的局部整体滑移特性(图9)，可从如下几方面考虑。

(1) 从能量角度考虑。提出了重力驱动稠密颗粒流的系统动能级数符合的单峰形概率密度分布，并依据统计分布规律定义了能级标准差和能级跨度(图10)。采用能级跨度和能级标准差将重力驱动稠密颗粒流细分为3个子流态(表1)，分别为：极缓慢流(能级跨度SOE>1，能级标准差σ<0.1)、连续流(SOE<1，σ<0.1)和间歇流(σ>0.1)[38]。

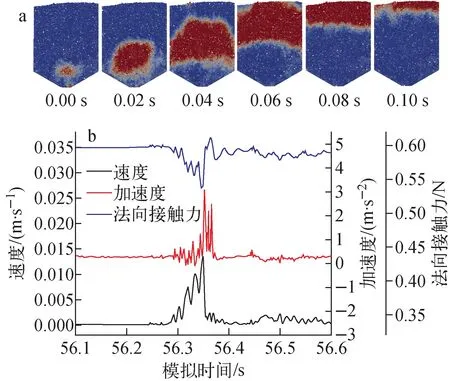
a——发生整体滑移的流场演化过程； b——对应的速度、加速度、法向接触力的变化图9 球床内颗粒速度场的整体滑移特性Fig.9 Whole slip characteristic of particle velocity field in pebble bed

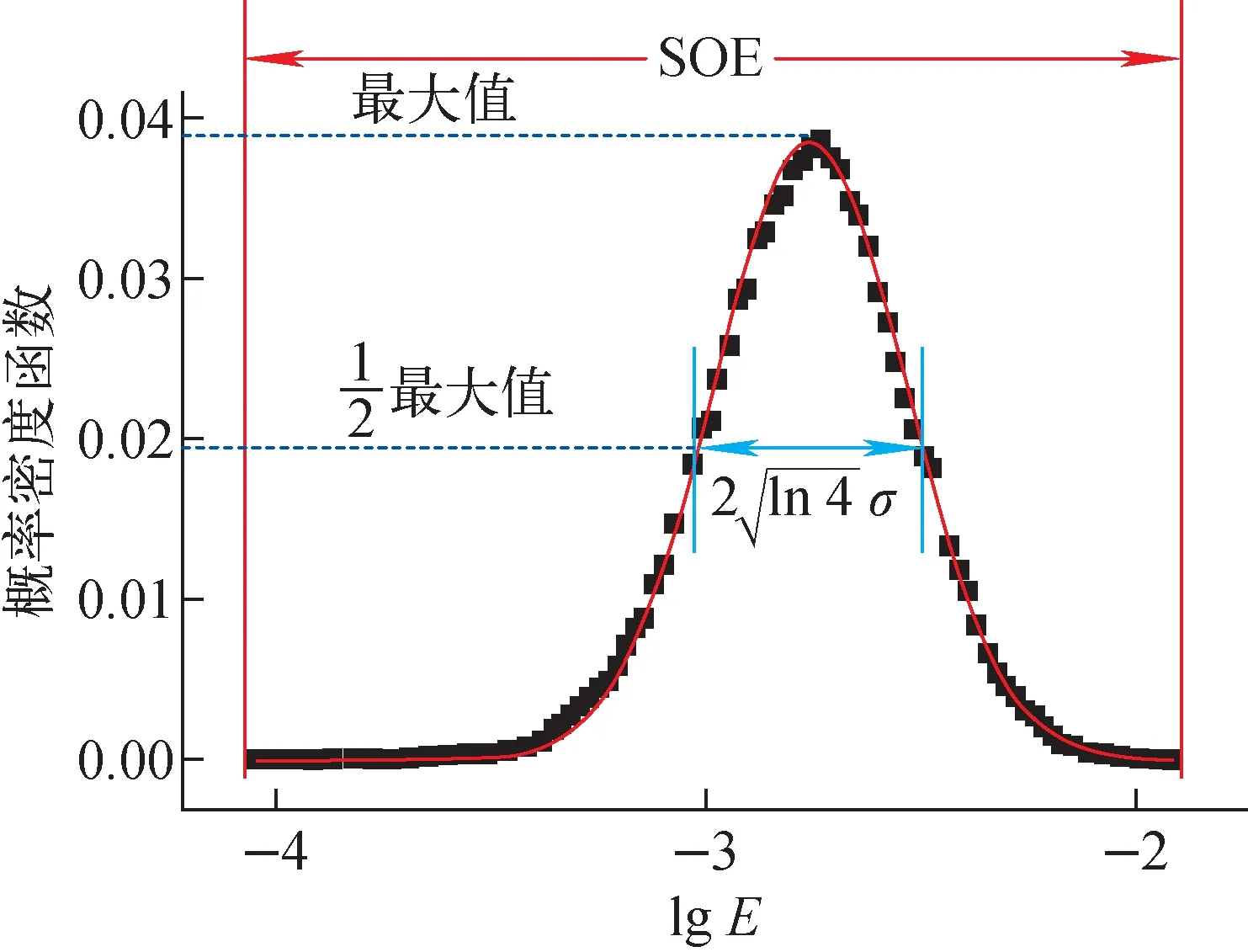
图10 能级跨度和能级标准差Fig.10 Span of energy magnitude and standard deviation

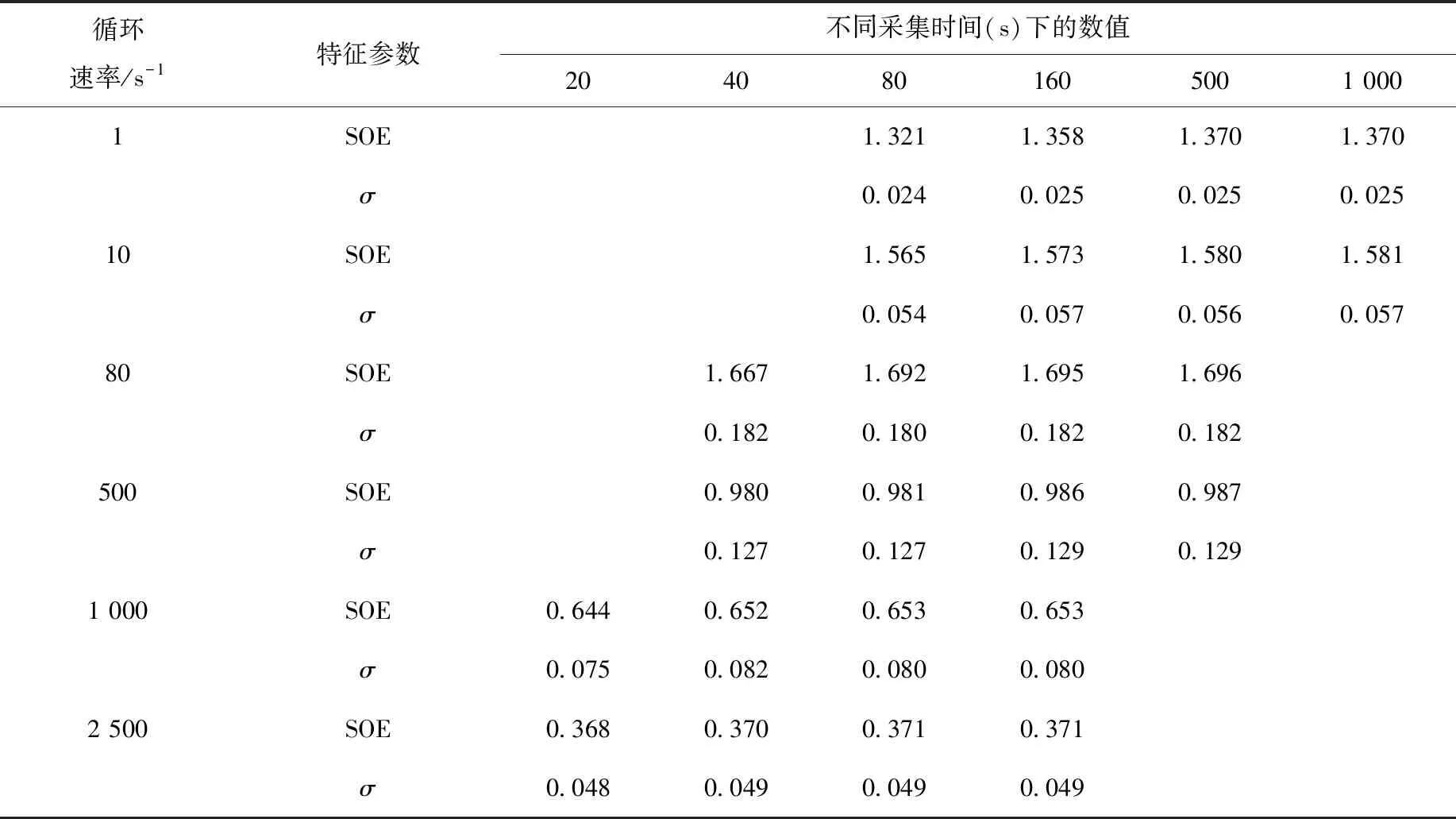
表1 流态划分采集时间独立性检验Table 1 Independence test on simulation time

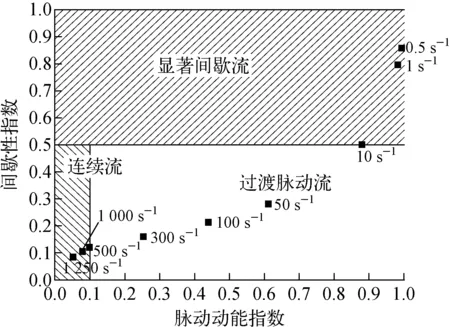
图11 基于参数分析的稠密颗粒流细分流型图Fig.11 Diagram of parameter analysis for categorizing dense pebble flow

(2) 从流动间歇性特征角度考虑。首先采用无量纲的脉动动能指数(RPKE)描述颗粒流的脉动性。并基于多重分形分析提出了间歇性指数C，表征了相邻脉动运动的平均时间间隔，在时间尺度上描述连续均匀运动的相对时间。基于C和RPKE，将其分为3种典型流型(图11)：显著间歇流(C≥0.5)；连续流(C<0.5，RPKE≤0.1)；过渡脉动流(C<0.5，RPKE>0.1)。显著间歇流，球床内颗粒球在JP3绝大多数时间内保持接近于静止的状态。此时，脉动运动以较大的速度为特征，相邻脉动运动的平均时间间隔较大。连续流，球床流场呈现较快的流动速度，其对应的颗粒流动呈现较小的脉动特性，流动较为平稳。过渡脉动流，涵盖了明显间歇流到连续流的过渡区域[39]。

(3) 从主导流态的机理因素考虑。将动力学量主导的流态称之为动力学流态，典型的表征量是颗粒受力(或加速度、位矢的二阶导数)；对应地将运动学量主导的流态称为运动学流态，典型的表征量是速度(位矢的一阶导数)。在数学上相关系数为正则化的协方差，表示两个独立变量之间的关联性，其值为1或-1表示正相关或负相关，0表示不相关。对球流的平均速度和平均受力进行相关性分析，可发现在高速球流中力的相关系数ρFF无明显周期性，而低速球流中ρFF有明显周期性和主频(图12a)；反之，在高速球流中速度的相关系数ρVV有明显周期性和主频，而低速球流中无明显周期性和主频(图12b)[40]。

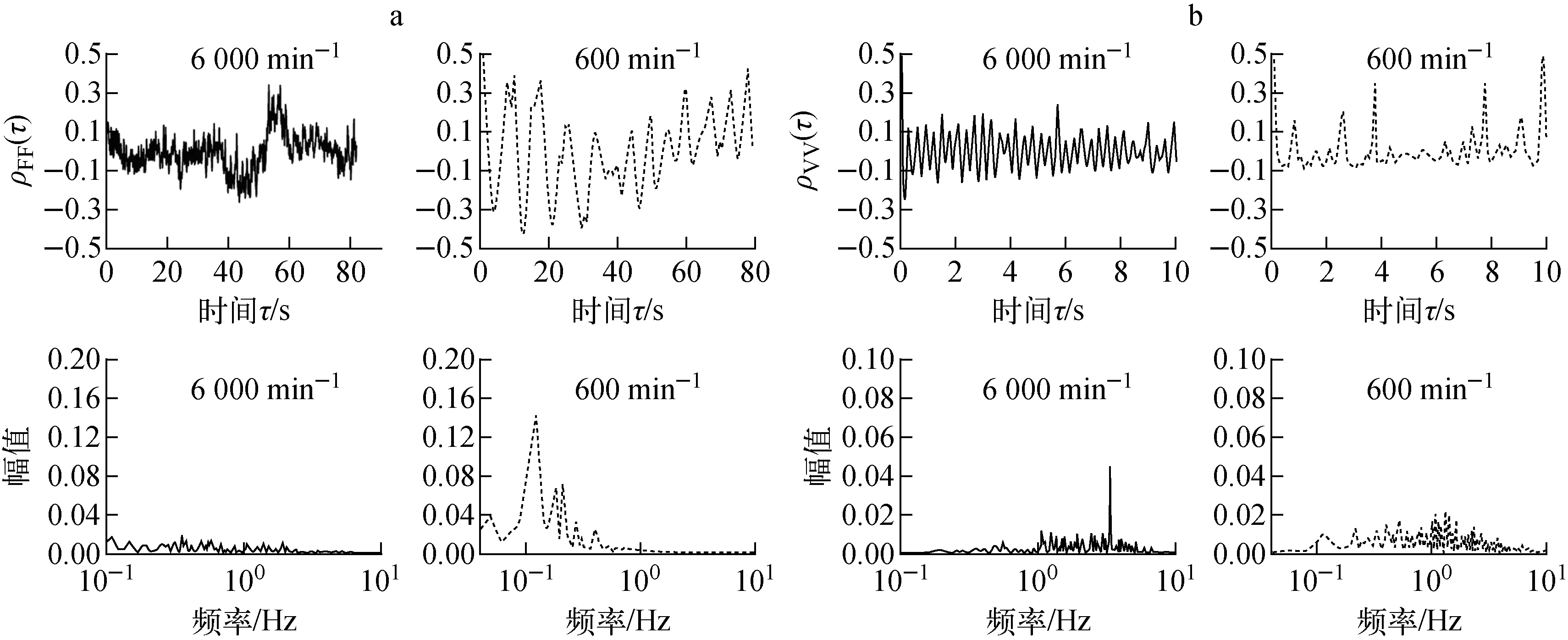
图12 球床受力和速度的相关系数及其频谱Fig.12 Autocorrelation functions and power spectra of mean force and mean velocity

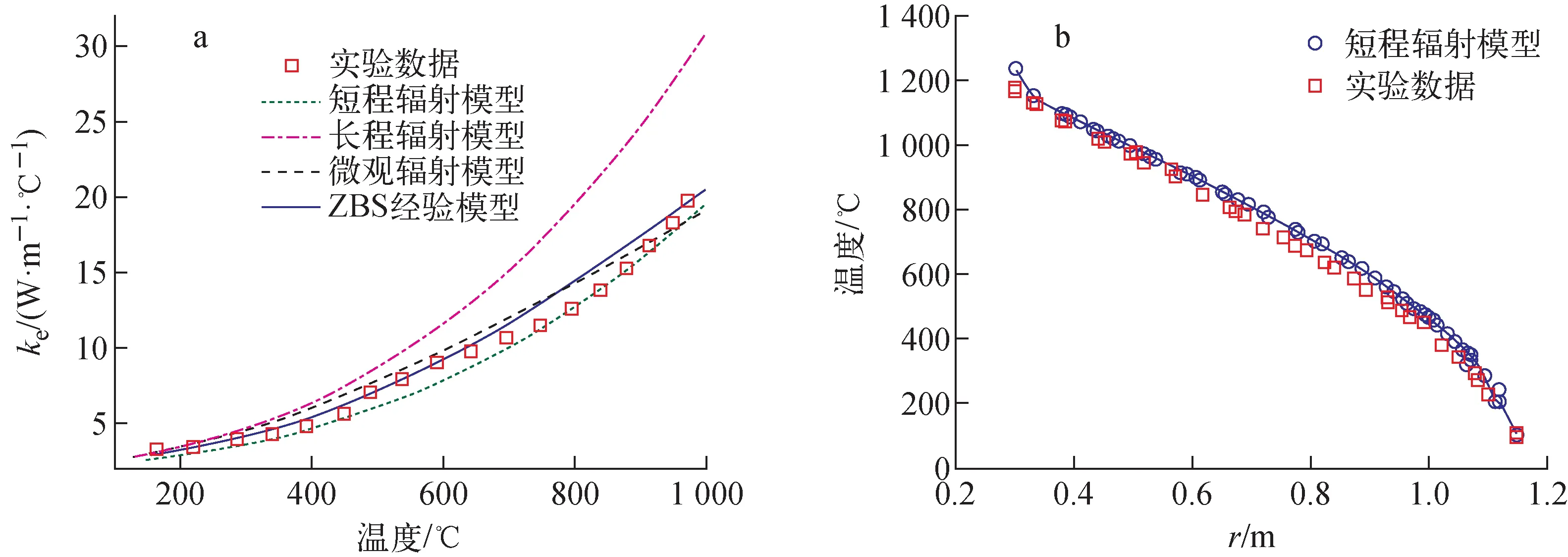
图13 短程、长程和微观表面辐射模型对球床等效导热系数估计的对比(a) 以及短程辐射模型与南非HTTU实验结果的比较(b)Fig.13 Effective thermal conductivities predicted by short-range, long-range and microscopic radiation models (a) and comparison of simulation results obtained by short-range radiation model with HTTU experiment result (b)

2.2 球床高温热辐射模型

为采用数值方法研究球床高温辐射，在不同空间尺度下建立了长程辐射模型(LRM)与短程辐射模型(SRM)、微观表面辐射模型(MSM)，以及亚颗粒辐射模型(SCM，又称子单元辐射模型)[41-45]。长程辐射模型中考虑了所有存在辐射换热关系的颗粒对，而短程辐射模型仅考虑距离较近的单层Voronoi单元相邻颗粒对。因模型中认为材料内导热系数为无限大，结果表明当颗粒材料导热系数远大于辐射有效导热系数时，长程辐射模型适用于高温球床辐射计算，但当两者在同一数量级时，长程模型高估了材料内导热系数的影响，而短程模型因截断了长程辐射热流，从而抵消了对材料导热系数的高估，显示出良好的计算精度[41]。微观表面辐射模型通过对颗粒表面的详细剖分并详细计算角系数，呈现较高的计算精度，但其计算量过于庞大，无法满足存在大量颗粒的球床工程计算的需求。图13示出短程、长程和微观表面辐射模型对球床等效导热系数ke估计的对比以及短程辐射模型与南非HTTU实验结果的比较。图中，ZBS为Zehner-Bauer-Schlünder。图14示出亚颗粒模型预测的等效辐射导热系数kr与短程辐射模型、经验模型的比较。

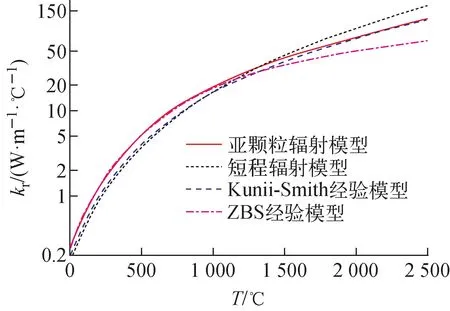
图14 亚颗粒模型预测的等效辐射导热系数 与短程辐射模型、经验模型的比较Fig.14 Effective thermal conductivity for particle radiation predicted by SCM and comparison with SRM and empirical correlation results

进一步，推导出了短程辐射模型和亚颗粒辐射模型下材料有效导热系数的解析表达式。计算结果表明，短程辐射模型在温度超过1 200 ℃时略有偏高，而亚颗粒辐射模型是通用的理论性方法，在超高温度下(大于1 500 ℃)仍适用[44-45]。

3 总结

通过对清华大学核能与新能源技术研究院近几年对球流和球床等效导热系数的主要研究成果的回顾和总结，实验和模拟结果极大地加深了对球床反应堆的内在规律和机理的认识，给出了球床内关键工程参数的准确估计。因此，可认为球流实验和球床等效导热系数实验有效揭示了球流的基本规律，而球流模拟及基于元胞建模的颗粒辐射模型能为球流研究、堆芯优化、重要热工参数的估计和比较提供有效的帮助。

但球流仍存在较多需解决的理论、计算、实验和工程问题，仅列如下几方面。

理论方面：1) 如何给出能描述球流在拟连续介质力学框架中的力学本构方程，以能跨越离散介质和连续介质描述的鸿沟，实现理论的统一性；2) 如何给出极缓慢球流分区、缓慢与快速流动的物理本征特征及数学表达。

计算方面：1) 在离散介质力学模型方面如何开发更高效的算法，提高计算效率并保证计算精度；2) 如何开发球流计算与球床辐射导热计算、球床冷却剂流动传热计算的多重耦合模型及高精度算法。

工程方面：1) 如何给出球流的间歇频率、滞留特性与球床、球等几何、物性和运行参数之间的关系，以更好地指导球床堆在不同运行环境及应用中的反应堆设计；2) 球床球流设计与反应堆物理设计的接口及迭代问题。

上述内容是将来还可进一步深入探讨的问题，因此下一步将在球流全3D测量、球流及球床等效导热系数快速计算、球床式反应堆内的氦气和球流两相耦合及换热的测量和建模等方面进行深入研究。