高温气冷堆螺旋管式直流蒸汽发生器热工水力学

李晓伟，吴莘馨，张作义

(清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084)

高温气冷堆(HTGR)[1-5]采用氦气作冷却剂，所以其蒸汽发生器一次侧换热系数较低，传热管较长，因此采用螺旋管结构。除采用螺旋管结构外，高温气冷堆蒸汽发生器还有工作温度高、二次侧直流、一次侧氦气加热等特点。高温气冷堆蒸汽发生器热工水力与一般压水堆的U型管式自然循环蒸汽发生器存在本质区别[6]。压水堆蒸汽发生器热工水力分析工具、方法和结论不适用于高温气冷堆蒸汽发生器。

一般火电的亚临界直流锅炉的经验也不能直接应用于高温气冷堆蒸汽发生器。首先高温气冷堆蒸汽发生器是核一级设备，安全性要求高，需对其进行详细的热工和结构分析。高温气冷堆蒸汽发生器结构紧凑，螺旋管束间距小，压力壳内单位体积换热面积大，而直流锅炉水冷壁布置空间较充裕。另外高温气冷堆蒸汽发生器一次侧采用氦气对流加热形式，辐射加热几乎可忽略。

鉴于以上因素，需针对高温气冷堆蒸汽发生器热工水力进行程序开发和实验验证。本文针对高温气冷堆蒸汽发生器的基础热工水力、温度均匀性、两相流不稳定性等问题及其对应的一维稳态程序、一维瞬态程序、二维程序及理论方法进行阐述和分析。

1 基础热工水力及一维稳态程序

由于高温气冷堆蒸汽发生器采用螺旋管结构，所以其热工水力设计和计算的基础是有准确的横掠螺旋管管束及螺旋管内对流换热及流阻的数据或计算公式。由于高温气冷堆蒸汽发生器壳侧工质为氦气，其对流换热热阻较大，所以螺旋管内高温高压水直流蒸发过程换热系数计算的准确性就显得不紧迫。表1列出高温气冷堆蒸汽发生器的热工参数和几何结构，并与压水堆自然循环蒸汽发生器进行对比。

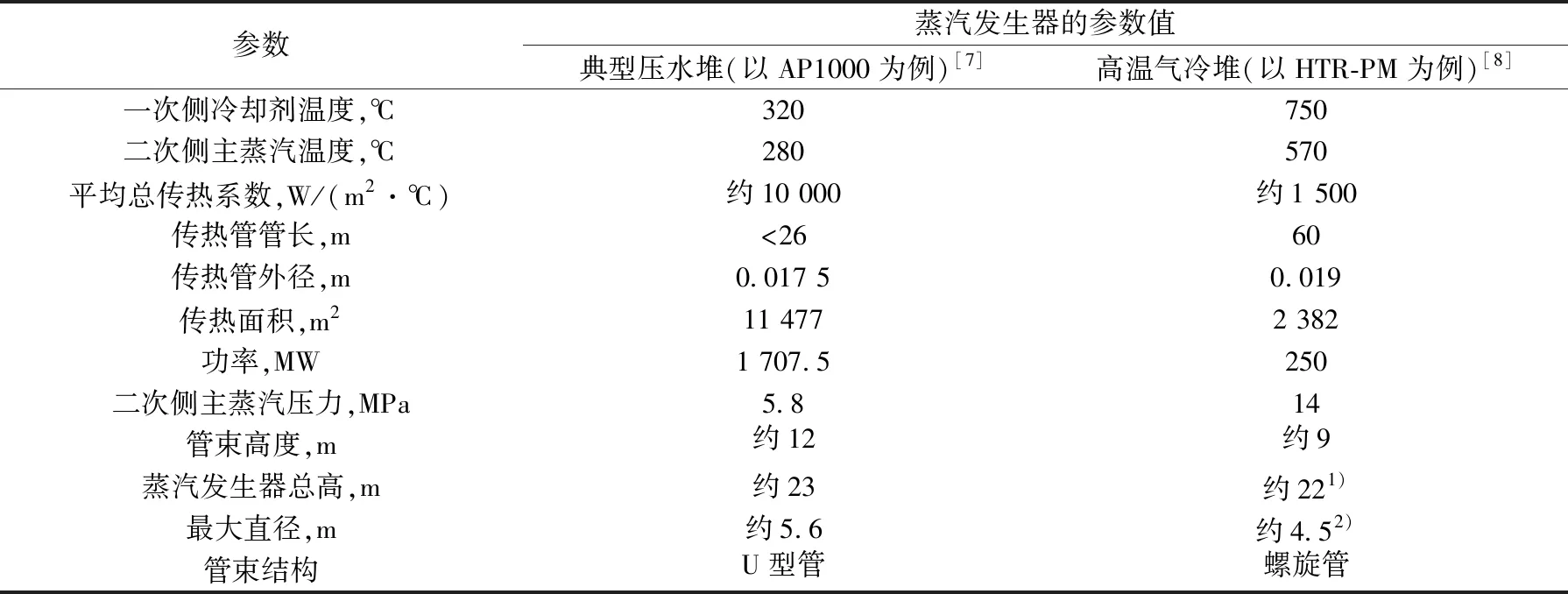
表1 高温气冷堆及典型压水堆蒸汽发生器热工和几何参数Table 1 Thermal hydraulic and geometrical parameter of HTGR and typical PWR steam generators

注：1) HTR-PM蒸汽发生器顶部集成氦风机，总高包含氦风机高度

2) HTR-PM蒸汽发生器顶部集成氦风机，最大直径为氦风机处壳体外径

1.1 螺旋管内单相流动换热

螺旋管内流动及换热特性与直管有较大区别，当螺旋半径较小或Dn[9]较大时[10]尤为明显。当螺旋管的螺旋升角较大时，进行阻力系数及换热系数计算时可采用纵向间距修正螺旋直径以考虑螺旋升角的影响。

由于离心力效应的存在，螺旋管内层流向湍流转捩雷诺数不再是2 300，转捩雷诺数推迟。目前有多个计算公式可用，其计算结果相差不大，主要与螺旋曲率(r0/R)相关，推荐使用Schmidt公式[11]：

(1)

其中：Recri为层流向湍流转捩雷诺数；r0为螺旋管半径；R为螺旋半径。

实际工况中螺旋管内流动一般均处于湍流工况。针对光滑螺旋管内单相湍流流动摩擦阻力系数，有较多的经验关联式可供选用[12-15]，推荐使用Ito公式[16]。而粗糙螺旋管内湍流流动摩擦阻力系数公式非常少，推荐使用Zhao等[17]的公式：

(2)

其中：ε为相对粗糙度；fhel为阻力系数；Re为雷诺数。式(2)对过度粗糙区到完全粗糙区均适用，属于半经验理论公式，实验验证范围为：Re为2×104～5×105时，ε为0.284×10-3～0.315×10-3。

螺旋管内湍流对流换热也有较多经验公式可供选用[12-14]，如Rogers等[18]的公式，Gnielinski[19]的螺旋管公式。另外杨世铭等[20]推荐的基于Gnielinski直管湍流对流换热公式[21]修正系数方法也较准确。对于螺旋管内层流对流换热，可参考文献[12]推荐的其他公式。

1.2 螺旋管内两相流动换热

由于高温气冷堆蒸汽发生器是对流加热，一次侧工质温度和热流密度有限，不可能出现第一类传热危机(偏离泡核沸腾)。但对于直流蒸汽发生器，第二类传热危机(蒸干)不可避免。实际上对于对流加热直流蒸汽发生器，不像电加热及核加热蒸发通道，由于对流加热与温差相关，蒸干点附近的管壁温升有限，且温度波动范围较小[22]。

两相对流沸腾流阻和换热较单相对流复杂，另外由于螺旋管内存在离心力效应，所以专门针对螺旋管内对流沸腾换热系数和两相摩擦阻力系数的公式较少。推荐采用直管经验公式加修正系数方法进行计算，因为直管经验公式验证范围广泛。对于直管内两相区(饱和沸腾及缺液区)的对流沸腾换热和阻力计算，可参考前苏联和我国的标准方法进行阻力及换热计算[23-25]。如果参数范围合适，也可采用专门的针对螺旋管内两相对流沸腾换热及阻力的经验公式，如Guo等[26-28]提供的螺旋管内两相流阻力及对流沸腾换热公式。也有人认为螺旋管内沸腾换热系数与直管差别很小[29-31]。

蒸干点的判断及干涸后换热可采用前苏联提供的基于直管的数据骨架表及相关经验公式[25]。对于直流蒸汽发生器，蒸干后管内对流换热系数会大幅降低，因此蒸干点的判断对于准确计算总传热系数具有重要意义，螺旋管内由于二次流的存在会使蒸干点位置发生改变，而目前缺乏针对螺旋管的专门判定公式，需进一步实验研究。由于离心力及二次流效应，螺旋直径较小、离心力效应较强的螺旋管内高温高压流体两相流流型及对流沸腾换热仍需要进一步研究[32]，这些研究会进一步促进螺旋管式直流蒸汽发生器热工水力的计算精度。对于中盘管及大盘管蒸汽发生器或换热器，由于离心力效应有限，单相及两相区的换热、阻力计算公式等与直管差别不大。

1.3 壳侧横掠螺旋管束对流换热

螺旋管式换热器热工设计的要点之一是要通过螺旋直径、管间距及每层螺旋管头数来尽量保证每根传热管长度基本一致。管束的横向和纵向间距除会影响对流换热系数及流阻外，还会影响管束的紧凑性及支撑结构的强度，需统筹优化考虑。

前人对横掠直管束对流换热进行了大量的实验研究，并总结出了较准确的经验公式[33-34]。横掠螺旋管束的流阻及换热计算也可采用前人总结的经验公式和成果。对于顺排管束，管束的横向间距(S1)对流阻及对流换热系数有较大影响，纵向间距(S2)对流阻及换热系数影响很小，但如果太小会导致流型发生转变而改变换热规律。对于叉排管束，S1及S2均对流阻及换热系数有影响[35]。

一般螺旋管束均接近于顺排管束，因此横向间距对螺旋管束壳侧阻力及换热影响很大。对于高温气冷堆蒸汽发生器热工设计及计算，横掠管束对流换热阻力及换热系数公式的准确性对于设计精度有很大影响。当相邻层螺旋管同向缠绕时，其流动与换热性能与横掠直管束基本相同，但需要修正由于螺旋升角导致的横掠管束气流攻角，可参考Zukauskas等[33]的实验结果。当相邻层螺旋管反向缠绕时，需适当考虑阻力系数及换热系数的减弱效应[36-37]。

1.4 一维稳态热工水力分析程序

与直管对流沸腾相同，螺旋管内亚临界水直流对流蒸发过程按传热形式可分为单相液态水对流传热、过冷沸腾、饱和沸腾、液膜强制对流换热、缺液区对流换热和过热蒸汽单相对流换热，按流型可分为单相流、泡状流、弹状流、环状流、雾状流等[25]。一般可将螺旋管内直流对流蒸发过程分为过冷区、饱和沸腾区、缺液区和过热区4个区域分别进行流阻及对流换热计算。如需更精确计算，可增加过冷沸腾区等。

针对一维单相、两相流体对流换热过程的控制方程(动量方程、能量方程)进行离散化，然后结合一次侧氦气及二次侧高温高压水工质的物性计算程序，以及横掠管束阻力及对流换热公式，将螺旋管内单相与两相阻力及对流换热量作为动量方程、能量方程源项，即可实现一维稳态热工水力设计分析程序[38-40]。

该程序可得出温度、压力、流速、换热系数等沿管长的分布。图1a示出德国钍高温气冷堆(THTR)蒸汽发生器100%功率时的氦气、水及管壁温度沿管长分布的计算结果与实际测量结果的对比。图1b示出HTR-PM蒸汽发生器75%功率时的计算结果与工程验证实验回路上测量结果的对比。图1a中，THe为一次侧氦气温度，Twater为二次侧水温度，Tw为管壁平均温度。

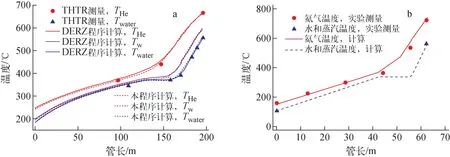
a——THTR；b——HTR-PM图1 高温气冷堆蒸汽发生器一维稳态程序计算结果与实验测量结果对比Fig.1 Comparison of calculation result obtained using one-dimensional steady state code with experimental measurement for HTGR steam generator

2 温度均匀性及二维分析程序

对于高温气冷堆蒸汽发生器，由于其工作温度非常高，传热管材料设计温度基本已达到现有材料的使用极限，需特别关注其最高运行温度，因此螺旋管束内部的温度均匀性就显得特别重要。例如对于Incoloy 800H材料，在675 ℃附近时，如果温度升高15 ℃，则其许用应力会降低10%[41]。与火电锅炉不同，核反应堆蒸汽发生器是不允许超过设计温度运行的。局部温度的小幅升高就会导致材料应力下降，因此必须要保证一定的温度均匀性。20世纪80年代，英国建造的AGR气冷反应堆的部分大螺旋盘管蒸汽发生器在调试初期出现了很大的温度不均匀性[42-43]，因此为降低管壁最高温度不得不降功率运行，最后虽然进行了大量的实验和分析并调节节流孔来降低温度不均匀性，也只将功率提高到设计功率的70%。

针对高温气冷堆螺旋管式直流蒸汽发生器可能出现的温度均匀性问题，清华大学核能与新能源技术研究院开发了两种二维计算程序，一种是基于CFD方法的管壳侧耦合二维计算程序，另一种是基于多孔介质模型的管壳侧耦合二维计算程序。两种方法均能计算壳侧管束的混合效应，可对不同层螺旋管的温度不均匀性进行计算和预测。基于CFD方法直接求解壳侧二维横掠管束对流换热，可用N-S方程直接计算壳侧温度混合，但其需要的网格及计算量较大。基于多孔介质模型的管壳侧耦合二维计算程序采用混合系数的方法来计算壳侧温度混合，其优点是网格及计算量较小，缺点是需要由实验或其他方法来提供较准确的混合系数。

2.1 基于Fluent二次开发的二维方法及程序

基于CFD软件Fluent二次开发的二维程序采用轴对称二维模型对螺旋管式蒸汽发生器进行数值模拟。壳侧横掠螺旋管束对流换热完全求解非稳态雷诺平均动量与能量方程，管内侧则只求解一维动量与能量方程。管侧一维模型解决了目前商业CFD软件计算直流蒸发过程的困难。壳侧对流换热方程的求解使用Fluent软件，管侧控制方程的求解及边界条件采用UDF来实现。

螺旋管内表面为对流换热边界条件，由于采用二维轴对称模型，每一管圈的温度及换热系数均相同。螺旋管内对流换热流体温度由管内流体焓值确定，首先给定水的入口焓值，然后第i+1圈水的入口焓值可由第i圈入口焓值加上第i圈的吸热量计算得到。第i+1圈内的水温度由管内流体焓值及压力计算得到。对流换热边界条件的对流换热系数和流体温度采用UDF来实现。基于该二次开发程序对螺旋直径等几何偏差，流量、温度、热辐射等热工水力偏差，堵管效应等对蒸汽发生器温度均匀性的影响进行了研究[38-39]。图2示出基于Fluent二次开发的管壳侧耦合二维计算模型及网格划分。

2.2 二维多孔介质程序

开发了基于多孔介质模型的高温气冷堆蒸汽发生器管壳侧耦合换热二维稳态程序SG-MIX[44]。壳侧横掠管束采用二维多孔介质模型实现，多孔介质模型不对横掠管束对流换热详细流场及温度场进行模拟，只对表征体元(REV)内的平均速度和平均温度进行模拟，因此网格可非常稀疏。壳侧多孔介质动量和能量方程采用有限体积法进行离散，用SIMPLER算法来处理动量方程中压力和速度的耦合，离散方程采用TDMA算法进行求解。由横掠管束带来的压降由动量方程的阻力源项进行模拟，管壳侧的传热量通过多孔介质能量方程的源项实现。不同管束间流道的温度混合效应由混合系数(Pe)来模拟。Pe采用管束混合效应实验或专门的数值模拟得到[45]。横掠壁面包围管束内部流场还会发生斜向流及瞬态周期性摆动，其对混合系数会产生较大影响[46-47]。

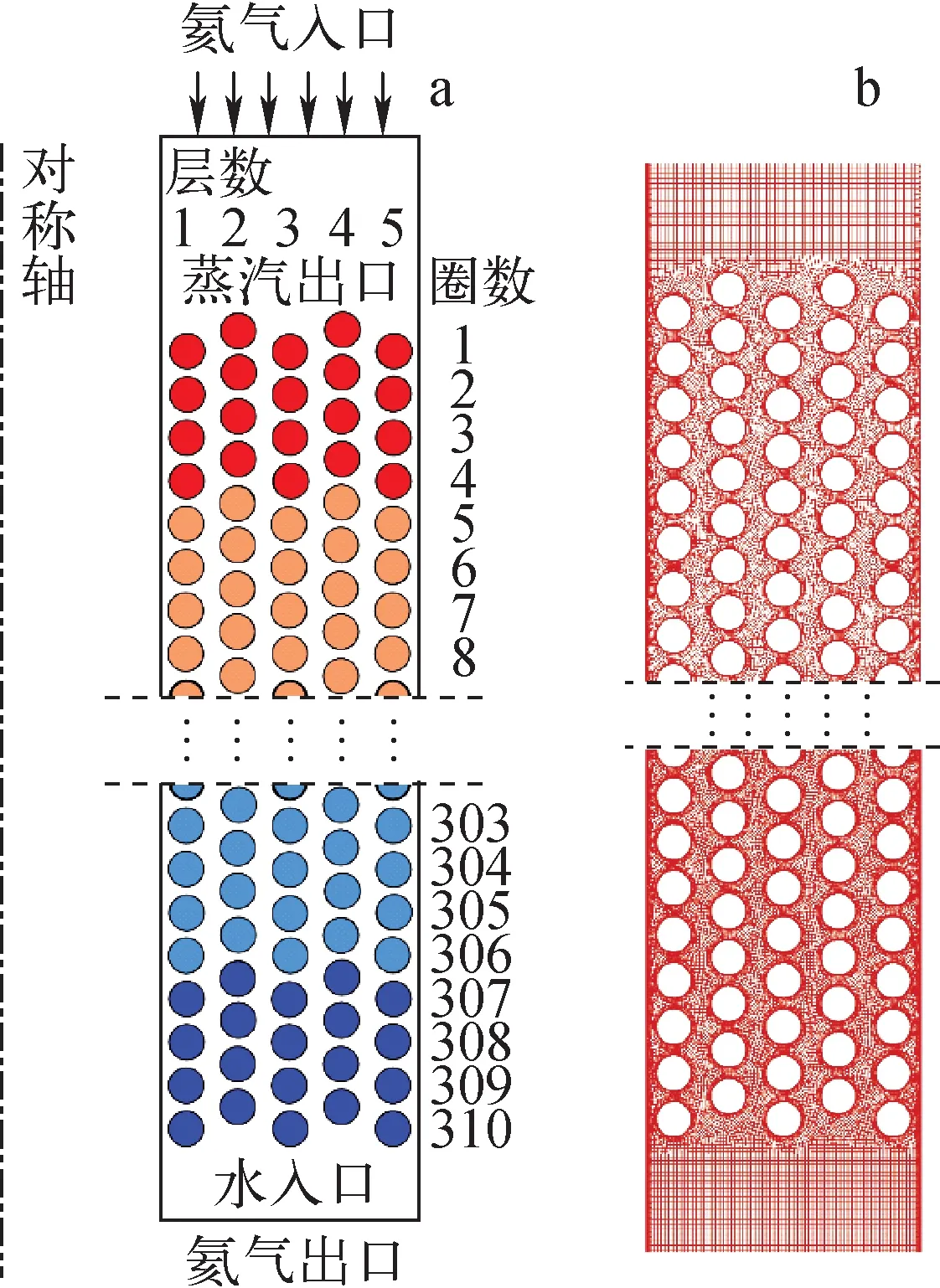
图2 管壳侧耦合二维计算模型(a)及网格(b)Fig.2 Tube and shell side coupled two-dimensional model (a) and grid distribution (b)

管侧采用一维模型。管壳侧通过热量传递进行耦合，从而实现了对蒸汽发生器管壳侧耦合二维数值计算。基于SG-MIX程序可研究螺旋直径等的几何偏差，流量、温度等的热工水力偏差，堵管效应等对蒸汽发生器温度均匀性的影响[44]。该程序计算结果比PODMIX程序[48]的考虑因素更为全面，计算结果更精确。图3示出基于多孔介质模型的管壳侧耦合二维计算程序需要的网格精度，与图2对比可见网格数量大幅减少。基于多孔介质模型的管壳侧耦合计算程序可较容易实现三维计算。

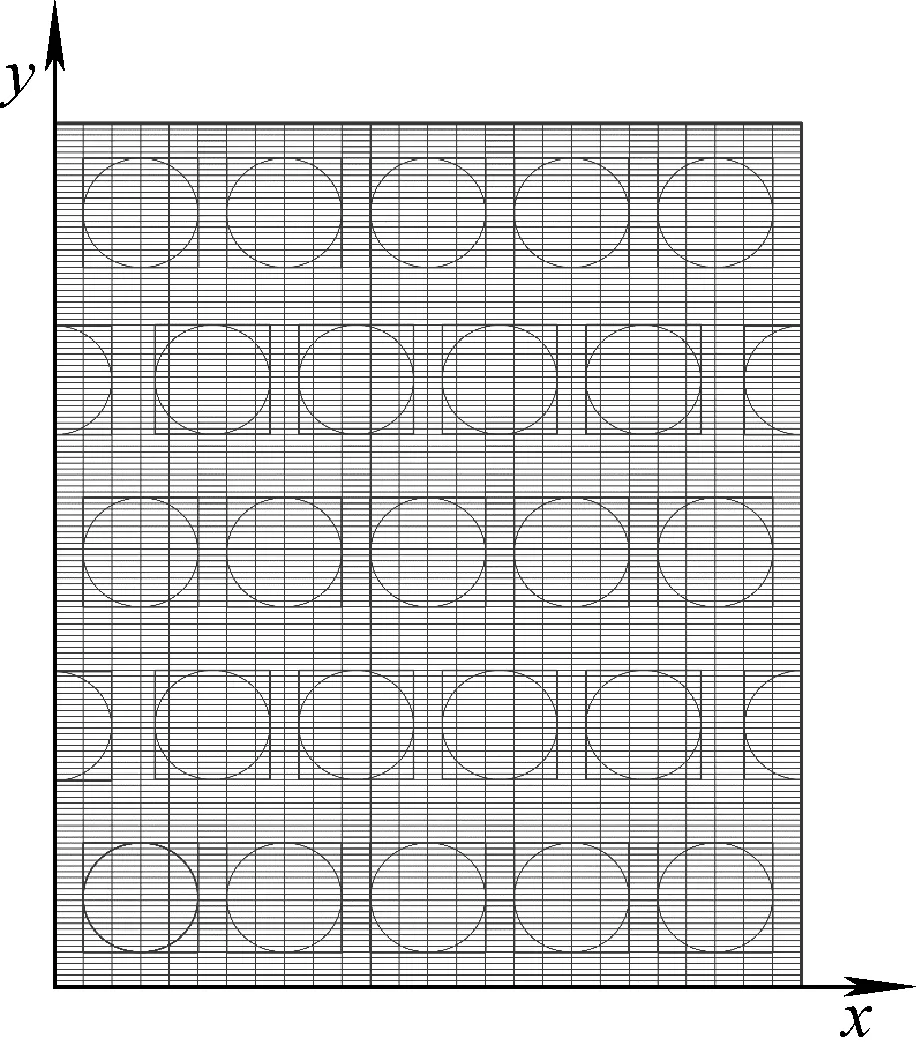
图3 基于多孔介质模型的 管壳侧耦合二维计算程序网格Fig.3 Grid distribution for tube and shell side coupled two-dimensional code based on porous media model

图4示出HTR-PM螺旋管式直流蒸汽发生器30%功率时5层传热管平均出口蒸汽温度分布的计算和测量结果。由图4可见，两种计算方法的结果与实验结果比较吻合。

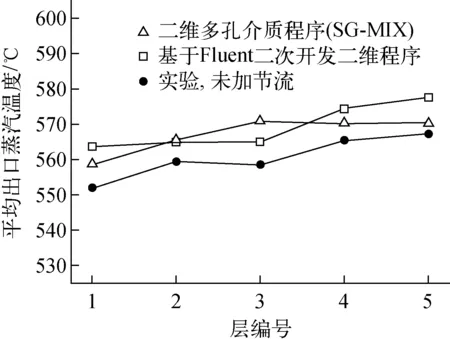
图4 不同层平均出口蒸汽温度的分布Fig.4 Distribution of average exit steam temperature in different layers

3 两相流不稳定性及其分析程序和方法

蒸汽发生器运行过程中要避免出现两相流不稳定，对于一款新型蒸汽发生器必须进行充分的分析和实验验证。在核反应堆蒸汽发生器[49]、核电沸水堆[50]、钠冷快堆直流蒸汽发生器[51]及化工、航天等其他领域[52]的两相回路中均出现过两相流不稳定性。两相流不稳定性不仅干扰控制系统，严重时还会导致传热管发生机械振动和热疲劳损坏，甚至烧毁。由于两相系统及两相流不稳定性的复杂性，在采用不同方法进行预测时需对边界条件和物理模型进行简化，这都会对预测结果的准确性带来影响，后面将会对模型边界条件及系统参数对不稳定性影响进行讨论。

两相流不稳定性有不同的表现形式，如整体流量漂移、整体流量脉动、管间脉动等。按机理两相流不稳定性又可分为静态不稳定性和动态不稳定性[53-56]。静态不稳定性是指系统流量从最初的工况点转移到另外一个工况点。静态不稳定性需要系统的水动力特性存在三次曲线并与外部泵特性曲线存在多个交点，一般消除三次曲线即可消除静态不稳定性。动态不稳定性指系统流量、压力和空泡份额等存在随时间的持续稳定脉动。动态不稳定性按机理又可分为密度波型不稳定性、压力降型不稳定性和热力型不稳定性等。

密度波型不稳定性依据对流量反馈作用的具体压降种类不同又可分为第一类密度波振荡与第二类密度波振荡[25]。密度波型不稳定性是两相系统中最常见的两相流不稳定性，它可发生在三次曲线正斜率区。压力降型不稳定性的出现需要在加热管路的上游存在可压缩空间，且两相系统位于压降-流量曲线的负斜率区，在可压缩空间与加热管路互相作用下，流量产生了1个周期性漂移。消除系统的压降-流量曲线三次曲线或消除传热管上游的可压缩空间即可避免压力降型不稳定。

两相流不稳定性的判断方法可分为时域法、频域法和半经验方法等[56]，也可从能量原理的角度出发进行分析并提出判据[57-58]。前苏联出现过基于部分实验数据及计算机程序制作的预测不稳定性边界的线算图，曾被我国机械工业部作为指导性技术文件所引用[59]，是工程上较为简单的预测方法，但有些工况下预测直流蒸发管稳定边界时偏差稍大[60]。另外，Ishii等[61]提出了采用无量纲过冷数(Nsub)与相变数(Npch)来判断系统稳定性并描述稳定边界，并基于以氟利昂为工质的稳定性实验给出了基于过冷数和相变数的稳定边界。

3.1 频域法分析

频域法是指对管内对流沸腾一维控制方程进行拉普拉斯变换，一般得到流量扰动与压降脉动的频域传递函数，再利用奈奎斯特等理论和判据对传递函数的稳定性进行分析判断。由于频域法需要对一维控制方程进行理论推导，所以一般需要较多简化，如恒定压降边界条件假设、等热流加热边界条件假设、常物性假设、单相流体不可压缩假设等。20世纪60—80年代西方国家编制了较多的频域法程序，如steamfreq-x等[62]。

清华大学核能与新能源技术研究院针对高温气冷堆蒸汽发生器进行建模，建立了基于小扰动线性化的频域理论模型，对其两相流不稳定性进行了分析[63]，将对流蒸发过程分为单相水区、两相区及过热蒸汽区。单相水区及过热蒸汽区采用不可压缩假设，两相区采用均相流模型。分别对3个区域的控制方程采用小扰动线性化、拉普拉斯变换，推导出了相应区域的流量脉动与压降脉动的频域传递函数。然后利用边界将3个区域的传递函数相联系，得到了直流蒸汽发生器螺旋管对流蒸发过程的流量脉动与压降脉动的传递函数。通过求解传递函数的内奎斯特曲线，采用内奎斯特判据即可判定螺旋管式直流蒸汽发生器的两相流不稳定性及其稳定边界。采用线性频域模型对高温气冷堆蒸汽发生器两相流不稳定性进行了分析，如图5所示。

3.2 时域法分析

时域法就是直接对蒸发管内两相流的动量方程、能量方程进行理论分析求解或离散化求解，可直接得出流量、温度、压力等热工参数随时间的脉动曲线。时域法中针对控制方程的离散化求解与常规CFD方法相似，大多数程序是一维的。鉴于两相流模型及数值计算的发展，最近开始出现采用三维CFD方法对两相流不稳定性进行计算分析[64]。能够对两相对流换热系统进行瞬态模拟的软件一般均可进行时域法分析，如核工程领域的系统分析软件RELAP5[64-65]和CATHARE等。时域法需要求解蒸发管内的一维瞬态控制方程，计算量较大，但可得到脉动周期、振幅等脉动细节。

清华大学核能与新能源技术研究院基于一维稳态热工水力分析程序编制了一维瞬态程序[40，67]，对高温气冷堆蒸汽发生器内两相流不稳定性进行了分析，在其工作压力及设计工况下不存在两相流不稳定现象[40]。当系统降低功率至20%功率，系统压力降低至约5 MPa时才开始出现不稳定性现象，当在入口施加较大节流后系统趋于稳定。图6示出质量流量、出口密度及出口含气率随时间脉动的曲线。

除了通过将偏微分控制方程进行空间离散化进行数值求解外，也可直接对控制方程进行集总参数化和小扰动线性化处理，得到一组描述对流蒸发过程的一阶线性常微分方程组(集总参数模型)，进而通过常微分方程组系数矩阵的特征根判断系统稳定性，同时也可得到状态量的响应曲线，这也属于时域方法。

3.3 系统参数及模型边界条件对两相流不稳定性的影响

关于两相流不稳定性，从20世纪50年代以来已进行了大量的实验和理论研究，总结了一些定性经验，这些都有助于增加对两相流不稳定性的认识，并有助于设计和分析。目前各系统参数对不稳定性影响的主要结论为压力越高越有利于系统稳定，入口节流越大越有利于稳定，出口节流不利于系统稳定，流量越大系统越稳定，热流密度提高不利于系统稳定性等[56，60]。入口过冷度对稳定性影响存在拐点，低于拐点时过冷度越大越不利于稳定，高于拐点时过冷度越大则有利于稳定。

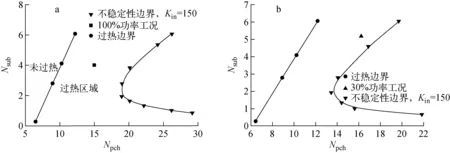
设计工况：a——100%功率；b——30%功率图5 螺旋管式直流蒸汽发生器的两相流不稳定性边界Fig.5 Two-phase flow instability boundary of helical tube once through steam generator

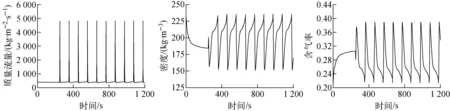
图6 不稳定性工况下不同参数随时间脉动的情况Fig.6 Parameter fluctuation with time under two-phase flow instability case

由于分析方法需对实际模型及边界条件进行简化，所以需研究不同边界条件对两相流不稳定性边界的影响。通过时域法及频域法对不同工况及边界条件下两相流不稳定边界进行分析，结果表明，对于多根并联蒸发管系统，进出口恒定流量边界条件稳定性好于恒定压降边界条件[68]，实际由泵提供给水的边界条件介于恒定流量和恒定压降之间。减小给水泵旁通流量、增加总管节流及总管长度，都使实际系统的边界条件趋向于恒定流量边界条件。轴向功率不均匀分布对两相流不稳定性边界有较大影响，沿流向功率递增分布的系统稳定性好于沿流向功率均匀分布的系统，沿流向功率均匀分布的系统稳定性又好于沿流向功率递减分布的系统[68]。高温气冷堆蒸汽发生器为氦气对流加热，由于入口氦气温度较高，所以沿流向功率递增(从水侧看)，因此采用均匀热流密度模型进行分析得到的结论是保守的。在一般传热管壁厚条件下，传热管管壁热容对直流蒸发管两相流不稳定性边界影响很小，因而忽略管壁热容的假设不会给频域法带来较大偏差[68]。

4 结论与讨论

高温气冷堆蒸汽发生器与压水堆U型管式自然循环蒸汽发生器有很大区别，本文阐述了高温气冷堆蒸汽发生器的基础热工水力学问题及针对这些问题所开发的相应程序。通过热工水力相关程序和软件，完成了高温气冷堆蒸汽发生器的热工分析。本文的研究方法和结论对具有相似参数的直流蒸汽发生器也具有参考和借鉴意义。

对于新型蒸汽发生器热工水力设计，不仅需要开发新的方法和程序进行充分的分析，还需进行充分的实验验证。大规模的工程验证实验台架或综合验证实验台架是必不可少的，综合验证实验台架可在实际运行工况下对热工和结构设计进行考验，其结果也可为瞬态复杂耦合程序提供验证。一般综合性工程验证实验耗资大、时间长、系统复杂、各种效应耦合。对于某些特定现象和问题，还可辅以较简单的分项实验加以研究，如横掠管束流阻及换热实验、管内单相及两相流动与换热实验、单根或少数并联管内两相流动不稳定性实验、流量分配及局部阻力实验等。这些分项实验可为相应程序提供较精确的实验数据，为程序开发提供更详尽的数据支撑。HTR-PM的蒸汽发生器除进行上述热工水力程序开发外，还进行各种分项实验，并建设了1∶1的工程验证实验回路，对1个螺旋管组件进行了实验验证。工程验证实验回路上的运行结果表明，高温气冷堆蒸汽发生器热工水力达到了设计要求[69-70]。