残缺区间合作博弈及其在农地污染治理中的应用

崔春生， 林 健

(1.北京物资学院 北京市智能物流系统协同创新中心，北京 101149; 2.福建农林大学 计算机与信息学院，福建 福州 350002)

0 引言

合作博弈是局中人通过结盟合作以实现尽可能大收益的竞争模型。大到国家与国家、集体与集体，小到人与人之间，都存在在广泛的竞争与合作现象。在潜在竞争的环境中寻求结盟合作的必要性日益凸显，合作博弈正是在这样的背景下日益发展起来。合作博弈的研究核心是局中人的收益分配问题，即合作博弈的解概念及其求解模型。Shapley[1]从局中人边际收益的概率加权期望值角度，提出了合作博弈的Shapley值。自Shapley值提出以来，在社会生产、行业经济等各个领域得到了广泛的应用[2～4]，已成为迄今为止最重要的合作博弈的解概念。

随着人类社会的不断发展，信息日益膨胀的同时其结构也在不断变迁。由于受知识结构、社会背景、所处环境等因素的制约，联盟的收益值经常不能准确获取，而往往以区间数的形式给出。特别是前期合作经验较少的联盟，此类联盟的收益信息很难预先准确评估，从而只能通过估算其收益的可能取值范围，来给出合作博弈的区间联盟值。基于上述背景及实践的需要，学者们已针对具有区间收益值的合作博弈问题展开研究，并提出了一系列有效的解概念。于晓辉等[5]通过拓展经典合作博弈的代数公理体系，将具有区间支付的合作博弈应用于供应链的协调利益分配。谭春桥等[6]基于解概念的严格公理体系，探讨了区间合作博弈的理论框架，并研究了区间Shapley值的存在唯一性。Alparslan-Goek[7]等通过定义具有区间支付合作博弈的相关概念，构建了在有效性、可加性、哑元性等框架下的唯一Shapley值公式。Han[8]等基于区间摩尔差运算和完全序，给出了一类新颖的合作博弈的区间Shapley值，探讨了该解存在的必要条件。通过引入系列类Shapley值的概念，进一步对相关结论进行了有效拓展。于晓辉[9]等结合区间数的运算性质，提出了具有唯一表达形式的区间合作博弈的区间Shapley值。

在合作博弈的应用过程中，由于合作博弈潜在的对抗性以及收益信息获取的复杂性，经常出现部分联盟的收益值无法获取的情形。针对这类信息残缺的合作博弈问题，Letscher[10]给出了具有残缺联盟值的合作博弈框架，分析了该框架下合作博弈的解概念。Housman[11]针对一类特殊的收益值残缺合作博弈问题，建立了残缺合作博弈的加权Shapley值，分析了该加权Shapley值满足的优良性质，验证了该值与传统Shapley值间的兼容性。Willson[12]在线性性、单调性、对称性等公理下，探讨了联盟收益值残缺的合作博弈的一类Shapley值。Masuya等[13]在合作博弈超可加性的基础上，定义了残缺合作博弈的上、下完全合作博弈，并定义了相应的有效Shapley值计算方法。林健等[14]通过定义残缺合作博弈的一致性，基于正、负理想分配，提出了一个满足存在性与合理性的理想Shapley值公式。Lin等[15]综合分析了互补联盟之间的超出值关系，并由此定义了残缺模糊合作博弈的最小二乘双核仁，分析了该解概念满足的公理性质。

本文首先给出了残缺区间合作博弈的基本概念，通过收益值信息的超可加特征，建立了联盟收益值的一致性检验模型。其次基于合作博弈的正、负理想分配，构造了收益分配与正、负理想分配之间的距离，并由此提出了残缺区间合作博弈的区间Ideal-Shapley值，分析了该值满足的合理性与存在性。最后将上述残缺区间合作博弈模型应用于农地污染治理的节约成本分摊问题，以突显本文方法的有效性与优越性。

1 区间合作博弈的基本概念

设全体局中人的集合N={1,2,…,n}，N的幂集记为P(N)。∀S∈P(N)，S称为N上的一个联盟。记R+={x|x≥0}，∀a,b∈R+，若a≤b，则称[a,b]为一个非负区间数。全体非负区间数的集合记为Ω+。

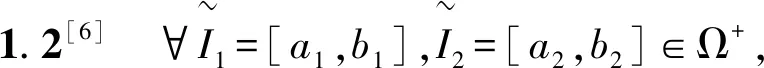
(1)k·[a1,b1]=[ka1,kb1],k>0；

其中运算“-H”称为区间数的广义Hukuhara差。

定义1.3[5]若对∀S1,S2∈P(N),S1∩S2=Ø，均有

(1)

v+(S1∪S2)≥v+(S1)+v+(S2)

(2)

v-(S1∪S2)≥v-(S1)+v-(S2)

(3)

超可加性是局中人形成联盟合作的基础，也是联盟维持稳定性的有效保障。当局中人形成合作后，由超可加性知，局中人的整体收益总和增加了。从而，合理分配大联盟的收益成为合作博弈研究的一个核心问题。

2 残缺区间合作博弈及其一致性扩充

由上述定义易知，残缺区间合作博弈中空联盟、大联盟以及单人联盟的区间收益值是已知的，这将是后续进行残缺区间收益值扩充的基础。

从模型(M-1)的约束条件易知，∀S∈Δ，指标集ε(S)不一定是唯一的。

为了获取残缺合作博弈中实数收益值的上、下可能边界，Masuya[13]基于超可加性给出了上、下完全合作博弈的定义，巧妙地分析了残缺合作博弈的潜在收益边界。通过对残缺实合作博弈元素扩充方法的区间拓展，可定义残缺区间合作博弈的上、下完全合作博弈如下：

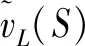
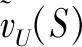
3 残缺区间合作博弈的区间Ideal-Shapley值

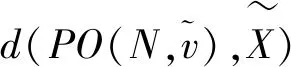
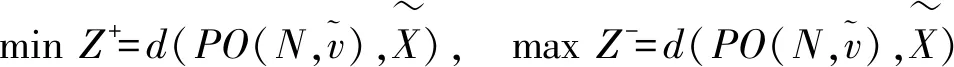
模型(M-2)的前两个约束刻画了区间合作博弈中局中人的个体理性，第三和第四个约束反映了大联盟的集体理性。第五和第六个约束条件是区间Shapley值的具体表达形式。第七和第八个约束条件是超可加合作博弈的必要特征，第九和第十个约束条件是上完全区间合作博弈和下完全区间合作博弈对残缺元素的扩充限制。根据区间Shapley值的有效性和合理性，故可略去模型(M-2)的前四个约束条件。假设大联盟对正、负理想偏差无额外的偏好，为了兼顾正、负理想偏差在最终分配确定时的作用，可将多目标优化模型(M-2)转化为相应的单目标优化模型(M-3)如下：

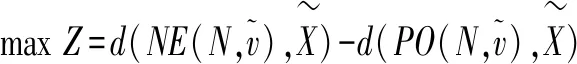
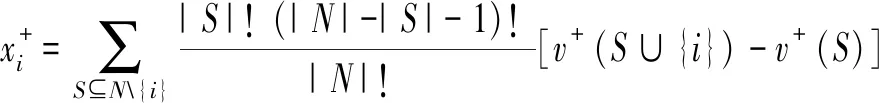
v+(S1∪S2)≥v+(S1)+v+(S2)

v-(S1∪S2)≥v-(S1)+v-(S2)

S1,S2,S1∪S2∈P(N),S1∩S2=Ø

|{S1,S2,S1∪S2}∩(P(N)Δ)|>1

单目标优化模型(M-3)中增加了约束条件|{S1,S2,S1∪S2}∩(P(N)Δ)|，确保了超可加约束中至少出现两个未知收益值，有效避免了冗余约束重复出现的问题，可很大程度上降低计算的复杂性。

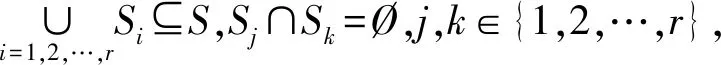
(4)

(5)

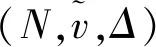
5 污染联合治理应用

设某城郊农地周边有三家化工厂(局中人1、2、3)，由于化工废水、废料等排放不当，现已导致工厂周边的农地出现严重的污染。为了维护农地的可耕作性以及人们的食品安全，当地政府责令这三家当事化工厂缴纳相应的治污费用，在停止排污的同时对周边农地进行污染联合治理。由于当地政府严格督促，当事化工厂也积极配合治污，经专家组估算在污染治理结束后会比预期节约成本12至18万元。由于各化工厂在治污人力、技术和维护等方面均存在优劣差异，对节约成本的再分摊方案也应兼顾治污各方的公平和效率。由于各化工厂间合作经验较少，故各联盟的节约成本值往往难以精确估计，更常见的是以区间估值范围的形式给出，甚至会出现某些联盟的节约成本值无法获取的情形。下面采用区间Ideal-Shapley值，给出农地污染治理的节约成本分摊策略。

化工厂1与其余两家化工厂有过频繁的前期交流合作，故彼此较为熟悉。但化工厂2和化工厂3之前没有合作过，导致联盟{2,3}的节约成本值难于预估。已知各联盟的节约成本值分别为：

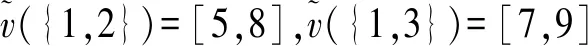
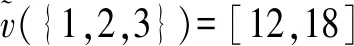
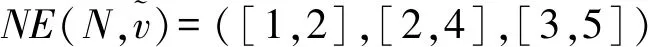
假设大联盟对风险保持中立，故可取参数λ=0.5。从而有

进一步，模型(M-3)可建立如下:

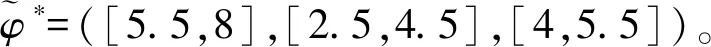
6 小结

随着社会生产与行业经济的不断发展，人类所处环境的复杂不确定性日益凸显。由于受知识结构、行业背景、社会环境等因素的制约，联盟的收益值往往无法准确获取，甚至有时会出现部分收益值完全未知的情形。本文针对部分收益值残缺的区间合作博弈问题，通过考察残缺区间收益值的上、下可能边界，构造相应的上、下完全区间合作博弈。基于超可加性验证了残缺区间合作博弈的一致性。定义了正、负理想分配，并由此构建区间Ideal-Shapley值的有效求解模型。结合农地污染治理的背景特点，将上述求解模型应用于节约成本的再次分摊问题，可为相关部门的实践应用提供必要的理论依据与数据支持。