另辟蹊径，解绝对值不等式

喻敏

（重庆市涪陵第一职业中学校，重庆 408100）

不等式是中学数学中的主要内容之一，很多章节的学习都要用到不等式的有关知识，其中不等式的解法是重点，而含绝对值的不等式的解法是难点之一。下面我就解含绝对值的不等式的解法谈点粗浅的看法。

众所周知，解绝对值不等式的基本思想，就是设法去掉绝对值符号，把不等式转化为不含绝对值的不等式进行求解，即将未知的知识转化为已知的知识，而化归思想也是我们认识新事物，研究新问题的重要方法之一。

去掉绝对值符号的方法主要有公式法、平方法等。而公式法是最基础的方法，其原理是将绝对值不等式转化为一元一次不等式进行求解。平方法则是将绝对值不等式进行两边平方，然后进行求解。在这里,我以例题向大家介绍一种敝人认为更简便的解绝对值不等式的方法——“八字口诀”法：变形、解方程、用口诀。

一、“八字口诀”解绝对值不等式的由来

教材上是这样来推导出绝对值不等式的解集的：

第一步：复习绝对值的几何意义

第二步：│x│=3的几何意义：数轴上到原点的距离等于3的所有点构成的集合。利用图形求出解为3和-3。

第三步：由│x│＜3的几何意义：数轴上到原点的距离小于3的所有点构成的集合得出解集为。

由│x│＞3的几何意义：数轴上到原点的距离大于3的所有点构成的集合得出不等式的解集为。

第四步：由│x│＜3和│x│＞3的解集，得出│x│＜a和│x│＞a（a＞0）的几何意义和解集，从而得出解不等式│x│＜a和│x│＞a（a＞0）的口诀：大于取两边，小于取中间。。

我对以上内容的理解为：形如│x│＜a或│x│＞a的解题关键是找出两个关键点（即，绝对等于a的两个数），然后再利用一元二次不等式的一个诀窍（大于取两根之外，小于取两根之内）写出不等式的解集。然后我将此类不等式的解法归纳为以下八个字：①变形（变形为│x│＜a或│x│＞a(a＞0)的形式），②解方程（│x│=a），③用口（利用口诀“大于取两根之外，小于取两根之内”写出绝对值不等式的解集）。现在就让我们一起来验证“八字口诀”的准确性。

二、用“八字口诀”解形如│x│＜a或│x│＞a(a＞0)的不等式

分析：法1：（1）题目中的形式和基本形式不同，故而要先变形为

（2）利用“大于取两边，小于取中间”写出不等式的解集。

（3）由于变形后的不等号为大于，故而此不等式的解集应该取两根之外，通过数形结合可以得出不等式的解集。

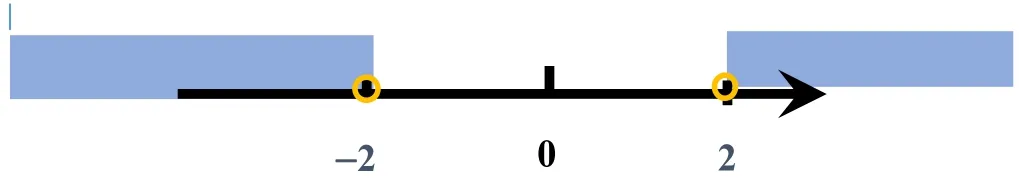
∴利用“口诀”：大于取两根之外，小于取两根之内求出不等式的解集为

注意：（1）根据不等式的符号确定解集时，一定是根据变形后的不等式的符号。

（2）由例题可以看出，“八字口诀”和公式法解绝对值不等式得出的解集一样，这说明“八字口诀”是正确的。

（3）由于变形后的不等号为小于，故而此不等式的解集应该取两根之内，通过数形结合可以得出不等式的解集。

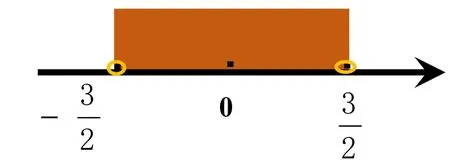
小结：由上面两个例题可以看出，“八字口诀”是可以用来解形如│x│＜a或│x│＞a(a＞0)的不等式的。下面我将接着用“八字口诀”解形如ax的不等式。

三、利用“八字口诀”解形如或（c＞0）的不等式

区别：绝对值里面的式子不同

联系：都是绝对值的不等式，形式相同。

（2）我们只需将2x+1看成一个整体m，那么形式就完全与相同了，即可利用“大于取两根之外，小于取两根之内”的口诀求出m的范围，然后再解方程2x+1=m就可以求出原不等式的解集了。

解：法1：令，则不等式变形为，即

现将m换成2x+1，可得

根据“口诀”：大于取两根之外，小于取两根之内可得不等式的解集为

四、利用“八字口诀”解形如的不等式

分析：此题看似比较复杂，学生一开始可能无从下手。现在我们可以将此题看成两个绝对值不等式和组成不等式组，然后再求不等式组解集即可。这就将未知的知识转化为我们已经学过的知识，从而降低了解题难度，所以解题关键在于将未知转化为已知。

2x-3＜5②

法1：设2x-3=m，则原不等式组化为m＞1③

m＜5④

解不等式③得m＜-1或m＞1 ⑤

解不等式④得-5＜m＜5⑥

将2x-3=m代入⑤得x＜1或x＞2；代入⑥得-1＜x＜4所以原不等式的解集为{x-1＜x＜1或2＜x＜4}

法2：令2x-3=1，解方程得x1=1,x2=2

即不等式①的解集为{xx＜1或x＞2}

令2x-3=5，解方程得x1=-1,x2=4，

即不等式②的解集为{x-1＜x＜4}

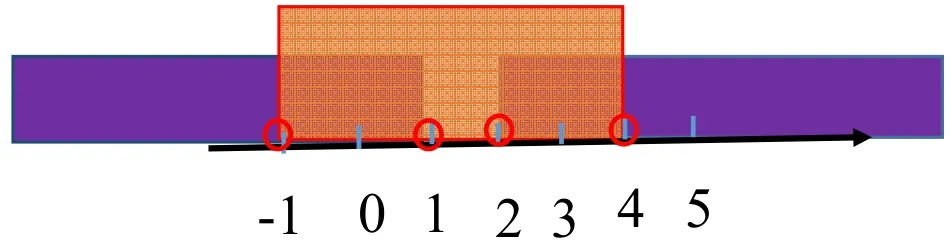
小结：由此可见，“八字口诀”仍然于解形如的不等式。

综上所述，“八字口诀”对于一般的绝对值不等式都适用。此方法将解一元二次不等式的方法（解方程，大于取两根之外，小于取两根之内）用到了解绝对值不等式之中，有效的将未知知识用已知的知识来解答，而且通过解答例题证明：此方法解形如和形如比教材上介绍的方法更简单、更准确。以上皆是本人个人观点，如有不对、不足的地方还请大家批评指正。