中国能源环境全要素生产率评价研究
——基于非期望指标的双前沿面网络DEA-Malmquist指数模型
2019-10-25
(福州大学 经济与管理学院,福建 福州 350116)
一、引言
改革开放以来,中国经济取得了迅猛发展,但大多数地区经济的发展模式仍然是以高投入、高能耗、高排放的粗放式增长方式为主,其导致的问题是资源消耗巨大、要素配置效率低下、环境污染日益严重,这显然不符合经济发展的可持续规律。为了能以最少的资源消耗、最低的环境代价实现中国经济又好又快且可持续地发展,必须关注能源环境因素,必须依赖能源环境全要素生产率的提高。而对中国能源环境全要素生产率进行合理评价是提高能源环境全要素生产率的基础工作,具有重要的现实意义。
目前有关能源环境全要素生产率的评价方法主要有参数评价法与非参数评价法,参数评价法主要有索洛余值法、随机前沿生产函数法等,非参数评价法主要是基于DEA的Malmqusit指数法。因为非参数评价法具有不需要对生产函数形式以及误差项分布做先验假设等优势,在近年来的研究中受到广泛关注。在国外文献中,Mahlberg等学者运用Malmquist指数法评价了欧盟14个国家的绿色全要素生产率,发现改善环境在一定程度上能提高生态效率[1]。学者Rácz和Vestergaard利用DEA-Malmquist指数模型对丹麦集中式沼气发电厂的能源全要素生产率进行了研究,分析了其在1992-2005年间内效率和生产率的变化[2]。学者Song和Zheng也利用DEA-Malmquist指数模型测算分析了中国安徽省热电企业的能源全要素生产率[3]。Mei和Chen以Malmquist-Luenberger生产率指数模型为基础,同时考虑资源和环境,并运用空间计量分析法测算中国省际全要素生产率的空间收敛性[4]。Wen等使用了双向定向距离函数和与其相对应的Luenberger生产力指数来计算北京在节能减排约束下的环境效率和环境全要素生产率[5]。Li等和Chen等将超效率DEA模型和Malmquist指数相结合,分别测算分析了中国各省的能源全要素生产率和长江经济带的环境全要素生产率[6-7]。
在国内文献中,马海良等学者运用超效率数据包络分析法和Malmquist指数法,评价了1995-2008年间长三角、珠三角和环渤海区域的能源效率和全要素生产率,并分析了全要素生产率分解后的各指标对能源效率的影响[8]。匡远凤和彭代彦将广义Malmquist指数与SFA模型相结合,对我国在考虑环境因素下的生产效率及全要素生产率进行了研究[9]。李小胜等学者基于中国30个省市1997-2011年经济增长和污染排放数据,利用 DEA-Malmquist指数法测算了环境全要素生产率指数及其分解结果[10]。吴明娥等将能源消耗和环境污染纳入经济增长核算范畴,评价了我国 30个省市的环境效率和全要素生产率的动态演变趋势[11]。李静和倪冬雪运用网络SBM模型和全局Malmquist指数法,测算分析了中国工业行业2001-2012年绿色生产和环境治理的两阶段的效率、全要素生产率及其构成[12]。汤杰新和马婷玉运用DEA-Malmquist指数法测算分析了中国环境全要素生产率和分解指数,研究表明技术进步对全要素生产率贡献最大[13]。韩瑞玲等对比分析了唐山市34个工业行业全要素经济生产率和全要素能源生产率及其分解结果,并对它们分别进行了影响因素分析[14]。吴卫红等和陈海跃采用 DEA-Malmquist指数法分别对中国的能源产业技术创新效率变动情况和能源全要素生产率进行了测算分析[15-16]。
由上述研究现状可知,目前已有的关于能源环境全要素生产率的系统评价,大多是基于单系统投入产出模型,即评价系统仍停留在单系统“黑箱”模型评价层次上,忽略了系统内部结构,因而无法探析出决策单元失效的更具体的原因。虽有学者考虑到了两阶段的情况,但仍然只是利用单系统模型分别对各子系统全要素生产率进行评价,而没有对考虑子系统联系下的系统整体的全要素生产率进行评价,这对于从整体上把握系统全要素生产率是明显的缺陷[12]。并且大部分学者使用的是传统的DEA-Malmquist指数模型,这种传统模型在对能源环境全要素生产率进行评价时仅考虑了乐观前沿面,而忽略了悲观前沿面,用该模型得到的评价结果无疑具有一定的片面性和偏差。基于上述认识,本文根据中国经济发展的实际情况,将整个经济系统分为能源利用子系统和环境治理子系统,在考虑非期望指标的基础上建立基于乐观、悲观双前沿面的网络DEA-Malmquist指数评价模型,并分别评价及分析每个子系统及考虑了子系统联系的系统整体的能源环境全要素生产率。
二、能源环境全要素生产率评价模型
根据中国经济的发展情况,可认为能源系统与环境系统是密不可分的,因为污染物的产生伴随着能源的消耗。因此本文将经济系统划分成两个相关联的子系统-能源利用子系统和环境治理子系统,如图1所示。
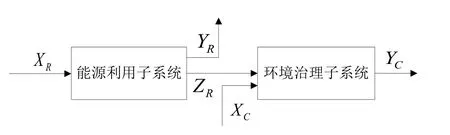
图1:经济系统两阶段模型图
假设有n 个决策单元,分别表示为DMUj(j = 1,...,n),XR(xR1,...,xRm)为能源利用子系统的初始投入向量,YR(yR1,...,yRs)为能源利用子系统的最终产出向量,ZR(zR1,...,zRf)为能源利用子系统的中间产出向量,同时也是环境治理子系统的中间投入向量。XC(xC1,...,xCb)为环境治理子系统的新增投入向量,YC(yC1,...,yCh)为环境治理子系统的最终产出向量。上述两个子系统共五个向量对应的权向量为vR、uR、ωR、vC和uC。对于决策单元j ,能源利用子系统投入、产出向量为xRj、yRj、zRj;环境治理子系统投入、产出向量为zRj、xCj、yCj。
假设两个子系统及整个系统均满足规模报酬不变,在这种条件下,每个经济系统整体以及各个子系统均在其各自的前沿面上存在相对应的投影[17]。构造虚拟链型系统时,原链型系统有n个,构造的虚拟链型系统也有n 个。因此,n 个虚拟链型系统与n个原链型系统共同建立起了一个次完美链型生产可能集T ,记为

应用DEA-Malmquist指数模型对能源环境全要素生产率进行评价时产出指标中既有期望产出(如GDP),又有非期望产出(如工业三废),而两者期望的方向不同,即期望产出越大越好,而非期望产出越小越好,为此就需要对非期望产出作出相应的处理。由于线性数据转换法可以不改变污染物的产出性质,又能有效地保持了DEA模型的凸性和线性关系,因此本文采用此方法来处理非期望产出。根据学者Seiford和Zhu的做法,将非期望产出与(-1)相乘之后再加上一个合适的正数,确保所有非期望产出均变成正数[18]。如z'=-z + v,其中v是一个足够大的向量。类似,对于非期望投入(第一子系统的非期望中间产出,也是第二子系统的非期望中间投入),人们希望其越多越好,因此也需要对其做类似的转换处理。
(一)能源利用子系统全要素生产率评价模型
对于能源利用子系统全要素生产率的评价研究,可以按三个步骤进行:第一步是构建能源利用子系统的乐观前沿面DEA-Malmquist指数评价模型,并利用其求得该子系统的乐观全要素生产率OMPIR及其分解结果;第二步是构建能源利用子系统的悲观前沿面DEA-Malmquist指数评价模型,并利用其求得该子系统的悲观全要素生产率PMPIR及其分解结果;第三步是根据前两步所求出的乐观和悲观全要素生产率及其分解,利用几何平均的方式,将基于不同前沿面的全要素生产率进行综合评价,求出基于双前沿面的能源利用子系统全要素生产率MPIR,以及分解后的技术效率变动ECR和技术进步变动TCR。
1.能源利用子系统乐观前沿面DEA-Malmquist指数评价模型
根据学者Färe的理论[19],测算基于乐观前沿面的DEA-Malmquist指数模型时,首先需求解其所需的4个距离函数,如模型(1)-(4)所示:

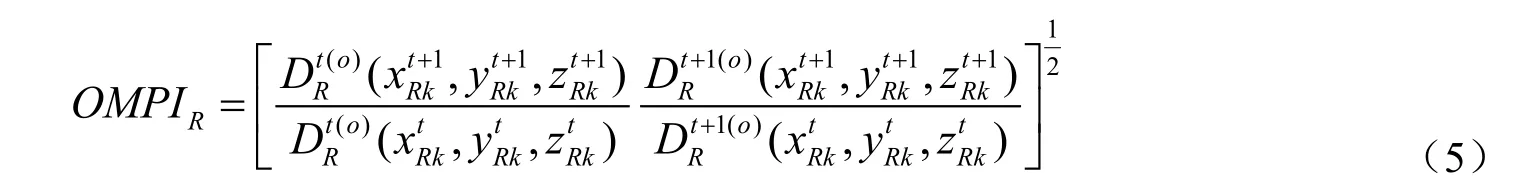
该指数是用来衡量能源利用子系统DMUk从t到t+1时期的乐观全要素生产率的变化情况。若OMPIR>1,则表示该子系统的全要素生产率是增长的,反之则是下降的,若OMPIR=1,则表示该子系统全要素生产率在两个时期之间未发生变化。该生产率指数还可以进一步分解为乐观技术效率变动指数和乐观技术进步指数,如模型(6)所示:
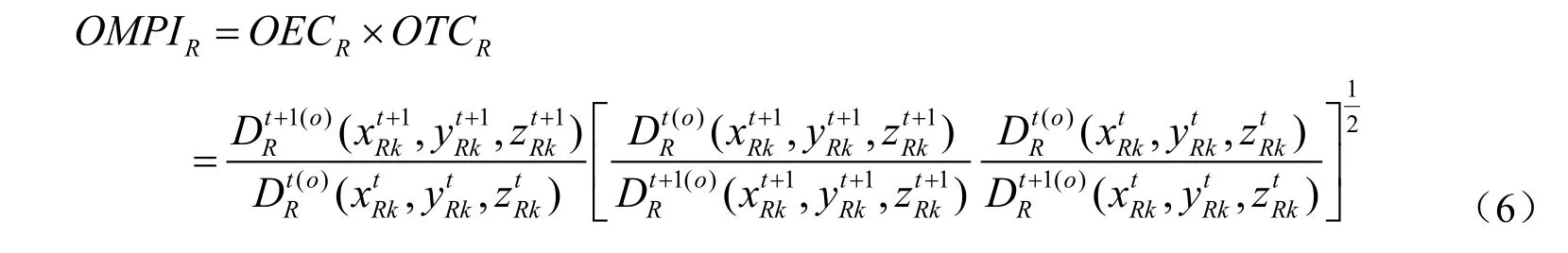
其中,OECR表示能源利用子系统DMUk基于乐观前沿面下的技术效率变动情况。当OECR>1,说明该子系统技术利用及组织生产的情况(即综合技术效率)得到改善,反之则说明技术效率恶化,若OECR=1,则表明技术效率无变化。而OTCR表示能源利用子系统DMUk基于乐观前沿面从t 到t+1时期的技术进步变动情况。当OTCR>1,说明该子系统技术进步,反之则说明技术退步,若OTCR=1,则表明技术水平不变。
2.能源利用子系统悲观前沿面DEA-Malmquist指数评价模型
传统的DEA模型仅基于乐观前沿面的角度进行研究,由此测算出来的结果无疑具有一定的片面性和偏差。因此,Wang等学者提出了悲观DEA模型[20],构造出一个最差即悲观的前沿面。基于悲观前沿面的DEA-Malmquist指数模型可先通过求解模型(7)-(10)获得4个距离函数:



其中,PECR表示能源利用子系统DMUk基于悲观前沿面下的技术效率变动情况。当PECR>1,说明该子系统技术效率得到改善,反之则说明技术效率恶化,若PECR=1,则表明技术效率无变化。而PTCR表示能源利用子系统DMUk基于悲观前沿面从t到t+1时期的技术进步变动情况,PTCR大于1、小于1和等于1,分别表示技术进步、技术退步和技术水平不变。
3.能源利用子系统双前沿面DEA-Malmquist指数评价模型
由于单纯地考虑乐观或悲观前沿面上的全要素生产率会使结果有失偏颇,根据Wang和Lan[21]的做法,用几何平均的方法将能源利用子系统两个基于不同前沿面下的全要素生产率指数进行综合评价,从而求出基于双前沿面下的DEA-Malmquist指数及其分解,具体如模型(13)所示:

(二) 环境治理子系统全要素生产率评价模型
与能源利用子系统类似,对于环境治理子系统全要素生产率的评价研究,同样可分成三个步骤:第一步是测算出基于乐观前沿面的 4个距离函数和在此基础上构建环境治理子系统的乐观前沿面DEA-Malmquist指数评价模型,并利用其求得乐观全要素生产率及其分解结果;第二步是测算出基于悲观前沿面的 4个距离函数和,在此基础上构建环境治理子系统的悲观前沿面DEA-Malmquist指数评价模型,并利用其求得悲观全要素生产率及其分解结果;第三步是利用几何平均的方式,将基于两个不同前沿面的全要素生产率进行综合评价,求出基于双前沿面的环境治理子系统全要素生产率,以及分解后的技术效率变动和技术进步变动。(该部分思想与能源利用子系统相同,只是投入产出名称和维数不一样,因受篇幅影响故省略。)
(三) 系统整体全要素生产率评价模型
对于系统整体全要素生产率的评价研究,类似于能源利用和环境治理子系统,也可分成三个步骤进行,即从三个层面(乐观、悲观和双前沿面)来构建系统整体的全要素生产率评价模型。
1.系统整体乐观前沿面DEA-Malmquist指数评价模型
在基于乐观前沿面的前提下,参考学者杨峰的两阶段理想前沿的网络DEA评价模型的建模思路[17],首先求出能源利用子系统DMUk的各个时期的最优值(由基于投入角度的相应模型求出,如模型(1)所示),从而求出能源利用子系统的各个时期的乐观前沿投入同理,算出环境治理子系统DMUk的各个时期的最优值(由基于产出角度的相应模型求出,如模型(14)所示),从而求得环境治理子系统DMUk的各个时期的乐观前沿产出


同理可求出其他三个距离函数,如模型(16)-(18)所示:



该指数表示的是系统整体DMUk从t 到t+1时期的乐观全要素生产率的变化情况。其中OMPIH大于1、等于1和小于1,分别表示系统整体乐观全要素生产率增长、不变和降低,该指数可分解成:

其中,OECH表示系统整体DMUk基于乐观前沿面从t 到t+1时期技术效率变动情况,而OTCH表示系统整体DMUk基于乐观前沿面从t 到t+1时期的技术进步变动情况。
2.系统整体悲观前沿面DEA-Malmquist指数评价模型
在基于悲观前沿面的前提下,首先求出能源利用子系统DMUk的各个时期的最优值(由基于投入角度的相应模型求出,如模型(7)所示),从而求出能源利用子系统的各个时期的悲观前沿投入同理,算出环境治理子系统的各个时期的最优值(由基于产出角度的相应模型求出,如模型(21)所示),从而求得环境治理子系统的各个时期的悲观前沿产出


同理可求出其他三个距离函数,如模型(23)-(25)所示:



该指数表示的是系统整体DMUk从t 到t+1时期的悲观全要素生产率的变化情况。其中PMPIH大于1、等于1和小于1,分别表示系统整体悲观全要素生产率增长、不变和降低,同样,该指数可分解成两部分:

其中,PECH表示系统整体DMUk基于悲观前沿面从t 到t+1时期技术效率变动情况,而OTCH表示系统整体DMUk基于悲观前沿面从t 到t+1时期的技术进步变动情况。
3.系统整体双前沿面DEA-Malmquist指数评价模型
与模型(13)类似可得,

MPIH指数用来衡量基于双前沿面下的系统整体DMUk从t 到t+1时期的全要素生产率的变化情况。而和分别表示系统整体DMUk基于双前沿面下的技术效率变动情况和技术进步变动情况。
三、中国能源环境全要素生产率评价及分析
(一)评价指标体系及数据来源
本文以我国29个省、市、自治区为研究对象,每个研究对象视为一个决策单元,分析中国2011-2016年能源环境全要素生产率的变动情况。其中所涉及到的数据来源于2012-2017年的《中国统计年鉴》、《中国环境年鉴》以及《中国能源统计年鉴》,由于西藏、青海部分数据缺失,因此未列入考虑范围,而港澳台与我国大陆的经济系统相差较大,同样不算在评价范围内。在具体评价的过程中,将这 29个省、市、自治区进行了东、中、西三大区域的划分[11],其中东部地区包括辽宁、北京、天津、河北、上海、江苏、浙江、福建、山东、广东和海南;中部地区包括吉林、黑龙江、山西、安徽、江西、河南、湖北和湖南;西部地区包括内蒙古、广西、重庆、四川、贵州、云南、陕西、甘肃、宁夏和新疆。
本文根据全面性、可比性、科学性等指标选取原则,并在借鉴学者奚萍芳的研究基础上[22],确定能源环境全要素生产率评价指标体系如下:将就业人口(万人)、能源消费总量(万吨标准煤)和固定资产投资(亿元)三个指标作为能源利用子系统的投入,将地区生产总值(亿元)作为该子系统的最终产出,而工业废水、废气和固体废弃物的产生量(万吨)三个指标既是能源利用子系统的中间产出,也是环境治理子系统的中间投入,将环境污染治理投资额(亿元)和环保人员数量(人)指标作为环境治理子系统的新增投入,而工业废水、废气和固体废弃物的排放量(万吨)三个指标作为该子系统的最终产出。其结构图如图2所示。

图2 :能源环境全要素生产率评价网络结构图
由于在年鉴上并未直接给出工业三废的产生量及排放量,考虑到指标数据的可比性及可获取性,本文利用工业三废中各自含有污染物总量进行代替,其中工业废水选取了化学需氧量与氨氧两种污染物,工业废气含有污染物二氧化硫、氮氧化物与工业烟(粉)尘,而工业固体废弃物则包括一般工业固体废弃物与危险废物。同时,为剔除价格变动因素,本文利用居民消费价格指数,以 2011年的价格为基准对固定资产投资、地区生产总值和环境污染治理投资额的价格指标数据进行了相应调整。
在搜集数据的过程中,发现 2016年的投入产出指标数据并不完善,有五个指标的数据残缺,分别为环境治理设施数、工业废水产生量、工业废气产生量、工业废水排放量和工业废气排放量。针对这几个缺失量,本文采用灰色预测模型中的GM(1,1)预测模型进行处理[23]。
另外,系统中的非期望指标为工业三废的产生量以及工业三废的排放量,本文根据前文所述的线性数据转换法来处理,即在上述构建的模型中,只需将非期望指标向量zRj(j = 1,...,n)和yCj(j = 1,...,n)通过线性数据转换法转化为和(文中v取各非期望指标的最大值加1),并用该向量替代原先的向量,代入模型中计算即可。
(二)评价结果及分析
本文采用MATLAB R2014a软件对2011-2016年间中国29个省、市、自治区的能源利用子系统、环境治理子系统及系统整体的能源环境全要素生产率进行评价,结果如表1、表2所示。

表1:2011-2016年各子系统及系统整体能源环境全要素生产率及其分解结果

表2:2011-2016年三大区域能源环境全要素生产率
1.能源利用子系统全要素生产率结果分析
表1中的结果是将不同时期的各效率指数经过几何平均方式计算得到的,因此表1的结果表示的是2011-2016年期间各效率指数的平均变动情况。从表1中可看出,中国能源利用子系统全要素生产率在2011-2016年间整体上呈现较为缓慢的降低,其年平均降低幅度为1.6%。从分解的结果来看,全国平均技术效率和技术进步变化均出现了不同幅度的降低,下降率分别为 0.4%、1.2%,说明两者均是导致能源利用子系统平均全要素生产率下降的原因。
具体来看,2011-2016年期间,中国只有少部分省市能源利用子系统全要素生产率出现不同程度的增加,具体有:河北、辽宁、黑龙江、浙江、江苏、湖南,增长率分别为 8.1%、4.6%、1.8%、1.3%、0.2%、0.1%。而大部分省市全要素生产率均出现下降,其中甘肃、贵州的下降幅度最大,降幅分别为9.9%、8.4%。从分解情况来看,2011-2016年间,能源利用子系统技术效率和技术进步变化在大部分省市是下降的,出现技术进步的省市只有3个,分别为河北(10.6%)、浙江(2.6%)、山东(1.3%)。
从表2中可看出,在评价期间内,中国三大区域能源利用子系统平均全要素生产率变化差异较大,其中东部地区能源利用子系统平均全要素生产率出现增长,增长率为 1.2%;而中部地区出现负增长,下降率达1.8%;西部地区下降幅度最大,跌幅达4.8%。
由以上分析可知,2011-2016年间,中国能源利用子系统全要素生产率整体上呈现负增长,全要素生产率负增长的原因是由于技术效率的降低和技术退步两者引起的,这说明对于大多数省市而言,技术效率和技术进步仍有改进的空间。因此,需协调好二者之间的联系,调整就业人员及固定资产投资的比例,优化资源结构配置,同时引进和开发新的技术及设备来促进全要素生产率的提高。
2.环境治理子系统全要素生产率结果分析
从表1中可看出,中国环境治理子系统全要素生产率在2011-2016年间出现较为缓慢的增长,其年平均增长率为 0.8%。从分解的结果来看,全国平均技术效率和技术进步变化均出现了小幅的提升,增长率分别为0.2%、0.6%,说明两者均对全国环境治理子系统全要素生产率的增长有正向推动作用。
具体来看,2011-2016年期间,中国有13个省市环境治理子系统全要素生产率呈现增长的趋势,其中河北、山西增长幅度最大,增长率分别为 4.2%、3.2%。仍有大部分省市环境治理子系统全要素生产率出现下降,其中浙江和北京的下降幅度最大,下降率分别达到了 8.8%、6.5%。从分解情况来看,2011-2016年间,环境治理子系统技术效率在大部分省市中均表现出增长的趋势,其中技术效率最高的省为陕西,增长率达1.8%。与技术效率变动特征不同的是,技术进步变化在大部分省市中均是下降的。
从表2中可看出,在评价期间内,中国三大区域环境治理子系统平均全要素生产率变化差异较小,其中东部地区环境治理子系统平均全要素生产率出现增长,增长率为 2.1%;西部地区全要素生产率整体上基本保持不变;而中部地区出现负增长,下降率为0.6%。
由以上分析可知,2011-2016年间,中国环境治理子系统全要素生产率整体上呈现增长的趋势,其增长的原因是技术效率改善和技术进步二者共同引起,这表明近几年中国政府在环境污染治理方面已略有成效,在某种程度上,有效控制了污染物的排放。
3.系统整体全要素生产率结果分析
从表1中可看出,2011-2016年间,中国系统整体能源环境全要素生产率出现下降,其年平均降低幅度为 1.5%。从分解的结果来看,全国平均技术效率有小幅增长(0.1%),而平均技术进步出现恶化(-1.6%),说明技术效率的改善一定程度上推动了全国系统整体能源环境全要素生产率的增长,而技术退步是制约全要素生产率增长的瓶颈因素。
具体来看,2011-2016年期间,中国系统整体全要素生产率处于增长趋势的省市只有5个,分别为河北(7.4%)、辽宁(3.9%)、天津(1.3%)、江苏(0.5%)和四川(0.2%)。大部分省市系统整体全要素生产率均呈现负增长,其中北京的下降幅度最大,降幅为10.4%。从分解情况来看,评价期间内,技术效率只在少部分省市中均实现了增长,其中黑龙江和辽宁的增长率最高,均为 4.2%;技术进步变化除了在河北(9.7%)、江苏(0.2%)和广东(0.2%)有小幅增长外,其余省市均呈现技术退步的情况。
从表2中可看出,在评价期间内,东部地区能源利用子系统平均全要素生产率出现略微增长,增长率为0.7%;而西部地区出现负增长,下降率为2.7%;中部地区下降幅度最大,跌幅为3.1%。
由以上分析可知,中国大部分省市能源环境全要素生产率均出现下降,然而2011-2016年间我国GDP每年都处于增长状态,这表明中国经济增长严重依赖于要素投入,这显然不具有可持续性。因此,需将经济增长转移到提高全要素生产率的轨道上来。
需要特别说明的是,大部分省市均出现了技术退步的情况,而这正是导致能源环境全要素生产率下降的主要原因。造成技术退步的原因可能源于两个方面:一方面,近年来资源短缺、环境恶化迫使中国各级政府将部分生产精力投入到节能减排中,而减少了对技术水平的关注,使得对节能减排的管制暂时减弱了技术进步程度;另一方面,中国存在着资本“过度深化”的现象,而资本投入的过快增长,必然会带来省级层面的产出投入比普遍下降的结果[9],产出投入比下降自然导致出现技术退步[24]。
四、结语
本文将经济系统划分成了能源利用子系统和环境治理子系统,建立了基于非期望指标的双前沿面网络DEA-Malmquist全要素生产率指数评价模型,并运用该模型评价了2011-2016年期间中国29个省、市、自治区的能源环境全要素生产率的变化情况,得出以下结论:对于能源利用子系统,中国大部分省、市、自治区全要素生产率均出现下降,其原因是由于技术效率的降低和技术退步两者引起的,因此有必要对这两方面作出相应的改善;对于环境治理子系统,中国 29个省、市、自治区年平均全要素生产率呈现缓慢的增长,其增长源于技术效率的改善和技术进步;从整体上来看,中国 29个省、市、自治区中绝大部分地区能源环境全要素生产率出现下降,其下降原因是由于技术退步引起的,而近年来我国GDP处于增长状态,这表明我国经济增长严重依赖于要素投入,粗放型增长特征明显,显然不具有可持续性,应将经济增长转移到提高全要素生产率的轨道上来。从三大区域划分来看,能源利用子系统、环境治理子系统和系统整体全要素生产率均只在东部地区出现增长,而在其他两大区域基本均出现下降。
