考虑锥向金属流动的大型锥形筒节轧制力计算模型

董志奎 彭利伟 焦云静 孙建亮，2 禚超越 赵静一卢明立 杨志明 王培亮

1.燕山大学机械工程学院，秦皇岛，0660042.燕山大学国家冷轧板带装备及工艺工程技术研究中心，秦皇岛，066004 3.江苏天明机械集团有限公司，连云港，222002

0 引言

大型锥形筒节主要应用在核电、石油、化工、航天等领域，是我国重点领域关键技术装备的关键零部件。目前大型锥形筒节的成形方法是自由锻，其缺点是能耗大、效率低，同时锻造筒节的尺寸精度差，表面上存在凹凸不平的锻痕，材料利用率低、成本高。轧制成形具有生产效率高、尺寸精度高、材料利用率高、综合成本低等优点[1-2]。目前大型直壁筒节已经实现轧制成形，如果大型锥形筒节能够实现轧制成形，则对创新设计大型锥形筒体轧制装备，完成大型筒体制造技术的升级，解决制约我国大型筒体批量化生产能力瓶颈，实现我国重点领域关键技术装备的自主化和产业化都具有十分重要的意义。目前关于大型锥形筒节的轧制，以及相关轧制设备和轧制工艺的研究只有少量报道，且实际中还无法进行试验验证。轧制力计算模型是锥形筒节轧制过程控制的关键模型,因此本文针对大型锥形筒节轧制过程的轧制力计算模型进行研究。

目前关于环形件轧制力计算模型的研究较多。华林等[3-5]利用小型环件轧机进行轧制实验时，根据实验数据对环件轧制中的轧制力性能参数及工艺参数进行了分析，并通过初等分析法建立了环件轧制的物理模型和力学模型。QIAN等[6]建立了环件沟槽截面的轧制咬入力学模型，并分析了咬入条件的影响因素。GUO等[7]建立了环件在径轴向的稳定轧制条件下的数学模型，并提出了一种合理的轧制工艺。PARVIZI等[8]基于上限法求解出了环件轧制力和力矩的解析解。蒋日东等[9-10]基于环件轧制过程与特征，建立了热轧的环件轧制模型，并提出了环件轧制过程的自适应与自学习控制结构。汤翼等[11]提出了在轧制过程中环件中心不在芯辊和驱动辊中心连线上的轧制几何模型，建立了环件的运动学参数与环件壁厚和轧制进给量之间的关系。罗晓东等[12]基于有限元仿真软件，研究了环件轧制过程中咬入和锻透情况、应力-应变分布、轧制力与轧制力矩等金属的变形规律。韩星会等[13]基于有限元对内台阶锥形环件的轧制过程进行了数值模拟，提出了轧制毛坯尺寸和轧制孔型的优化方案，并进行了实验验证。WANG等[14]研究了锥形环件虚拟轧制过程的关键技术。上述轧制力计算模型适用于小型环件，由于大型环件直径、高度和厚度大，金属变形规律复杂，上述模型并不适用于大型筒节轧制，但为大型筒节轧制提供了思路和基础。

关于大型筒节轧制力计算的研究，中国第一重型机械集团提出了一种大型筒节轧制设备及其轧制工艺[15]。程瑞敏[16]对大型环件成形过程的数值模拟进行了研究，极大改进了大型环件的工艺优化及尺寸精度。兰箭等[17]以缩比环件轧制实验和有限元数值模拟为基础，研究材料轴向转移模式及其变形机理，提出包含环件形状因素的成形性能评定方法。华林等[18]研究了大型环件的径轴向轧制工艺，揭示了大型环件径轴向轧制过程的变形规律和机理，分析了轧制过程中产生的问题和缺陷的实质,为实际的工业生产提供了依据。门正兴等[19]对大型筒体锻造成形中产生的缺陷进行分析，并提出了合理的预防措施及解决方法。孙建亮等[20]为了准确计算筒节轧制力，建立了一种基于切块法的考虑筒节不均匀应力分布的轧制力计算模型。张博[21]研究了2.25Cr1Mo0.25V 大型筒节高温轧制过程中微观组织演变规律。陈素文[22]基于条层法对大型筒节热轧三维变形进行模拟，研究了筒节宽展的分布规律。

上述主要是针对直壁筒节的研究，关于大型锥形筒节轧制成形的研究，施熔刚等[23]对三代核电蒸发器锥形筒体锻件各部位进行检验分析，为轧制大型锥形筒节的尺寸及性能要求提供了参考。王实[24]优化了大型锥形筒体轧机辊系布置和辊系参数，进行了锥形筒体轧制过程仿真。

由于大型锥形筒节存在锥度，必须考虑金属沿锥向的流动规律，因此本文提出一种考虑金属锥向流动的大型锥形筒节轧制力计算模型。

1 考虑锥向金属流动的轧制力计算数学模型

大型锥形筒节尺寸巨大、自重大，采用卧式轧制会产生巨大的轴向力，导致轧辊磨损严重和宽展不可控。本文采用大型锥形筒节立式轧制，轧制稳定性较好，其物理模型如图1所示。大型锥形筒节由若干支撑辊支撑，支撑辊为主动辊，转速与筒节转速相匹配，目的在于减小支承辊与筒节之间的摩擦力，进而防止筒节下端面的扭曲变形；轧制变形由主辊和芯辊完成，主辊和芯辊立式布置，均为主动辊，通过芯辊调节压下量和进给速度。为便于计算分析，作如下假设[22]：锥形筒节轧机轧辊为刚体；锥节为刚塑性体；忽略轧辊和筒节的弹性变形。

图1 大型锥形筒节轧制物理模型Fig.1 Physical model of large conical cylinder

大型锥形筒节不同于直壁筒节，由于锥度的存在，锥形筒节轧制过程中变形区金属沿锥向流动，为了理论解析计算出大型锥形筒节轧制力分布规律，本文采用分层法来计算，即将锥形筒节沿轴向分层，建立以锥形筒体轧制方向为x轴、轧辊中心线为y轴、锥形筒体轴线为z轴的三维坐标系，坐标原点o位于筒体小端面轧制变形区，垂直截面受力如图2所示。

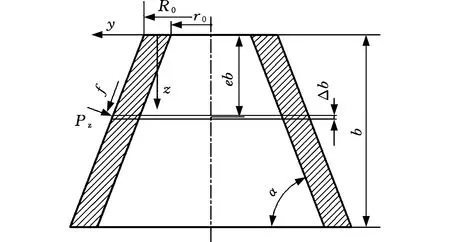
图2 大型锥形筒节垂直截面受力示意图Fig.2 Stress diagram of vertical section of largeconical cylinder

取任意一微层(图2)，根据几何关系，可得每一微层锥形筒体半径和轧辊半径：

(1)

式中，r0为锥形筒体最小端内壁半径；R0为锥形筒体最小端外壁半径；r为锥形筒体某一层内壁半径；R为锥形筒体某一层外壁半径；R10为芯辊最小端半径；R20为外辊最小端半径；R1为芯辊某一层半径；R2为外辊某一层半径；b为锥形筒体宽度；e为锥形筒体宽度系数，0≤e≤1；eb为选取层与锥形筒节小端的距离；α为锥形筒体倾斜角度。

式中，p为垂直方向单位压力。

由图3并根据外辊半径、芯辊半径、锥形筒节内外壁半径的几何关系，可得变形区厚度:

(2)

式中，H为变形区厚度；h为出口厚度；H1为变形区上半部分厚度，H2为变形区下半部分厚度。

图3 大型锥形筒节轧制示意图Fig.3 Schematic drawing of rolling large conical cylinder

式中，P为锥形筒节受到的轧制力；Pz为轧辊施加的总轧制力；f为锥形表面受到的摩擦力；μ为摩擦因数。

(3)

式中，Δh为每转压下量。

周波(1984-)，男，硕士，高级咨询师，主要研究方向为高校教育的法律问题及适用、企业思维下的学生管理方法研究。E-mail:48605299@qq.com

L≈xmax

下面对锥形筒节受力进行分析。根据图2中大型锥形筒节的受力分析，列出平衡方程：

(4)

根据建立的坐标系，由图3中各个圆弧的几何关系得出变形区的取值区间，在此区间轧辊与大型锥形筒节相接触。变形区的取值区间为

由于接触角足够小，故接触弧长[25]

则总的轧制力和锥形筒节变形产生的轧制力关系为

(5)

由于变形区上下轧辊直径和转速均不同，是典型的异步轧制，因此每一层的变形区可分为后滑区、搓轧区和前滑区，如图3所示的Ⅰ区、Ⅱ区和Ⅲ区，该层的前滑区(Ⅲ区)中，轧辊圆周速度的水平分量要大于金属流动速度，因此轧件上下接触面所受摩擦应力与轧制方向相同，轧件被拽入辊缝；在搓轧区(Ⅱ区)，轧件速度在外辊和芯辊速度之间，因此轧件的接触摩擦应力在芯辊与外辊接触的地方是相反的，该区域受到有利于金属变形的剪切力；在后滑区(Ⅰ区)，轧辊圆周速度的水平分量要小于金属流动速度，所以轧件上下接触面受到与轧制方向相反的摩擦应力，从而阻碍轧件运动。变形区中单元体受力见图4。

转变后的五建更加广泛地参与市场竞争，在全国各地摆开了战场。所到之处，力作频出，好戏连台，并在大型储罐安装、大型机组安装、大型电气仪表安装调试等方面，从无到有、由弱变强、由强而精，最终形成了具有自身独特风格的技术优势。

(a)Ⅰ区 (b)Ⅱ区 (c)Ⅲ区图4 变形区中单元体受力图Fig.4 The force diagram of the element in thedeformation zone

分析Ⅰ区的单元体受力情况(图4a)，在水平方向上受力平衡，平衡方程为

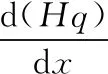
(6)

式中，q为水平方向应力；p1、p2分别为上下辊作用在变形区上的单位压力；θ1、θ2分别为p1、p2作用点与上下轧辊连心线夹角；τ1、τ2分别为上下轧辊与轧件接触面的摩擦应力。

(7)

式中，τxy1为变形区上半部分剪应力。

在Ⅰ和Ⅲ区，τxy1=2mk1y/H，在Ⅱ区，τxy1=mk1(其中，m为剪切系数；k1为上表面剪切变形抗力)。下半部分剪应力与上半部分类似。

由于咬入角比较小，故断面上剪应力对垂直方向平衡方程的影响可以忽略不计，可得

p1+τ1tanθ1=p2+τ2tanθ2=p

(8)

对于现代护理教育来讲，应面向未来、面向世界、面向现代化[9]。国际护理教育现阶段已成了比较完善和科学的护理教育体系，但是现阶段我国护士学历水平、护理教育水平相对较低，所以应积极开展继续教育，让护理人员的整体素质得以提高，满足现代护理的实际发展需求。

那是一个晴朗的上午，我漫步在人来人往的街道，太阳发出的光芒照在我的脸上，暖暖的。路，走到一半，一个舞蹈班的招生广告吸引了我，上面用了几个粗体大字写着：舞蹈班招生，被选中的孩子可以去广场参加演出。我非常想去，因为我从来没有参加过演出，我渴望舞台的光鲜和掌声。我飞快地跑回家对妈妈说：“妈妈，我想去学习舞蹈，想去参加演出。”妈妈先是一愣，然后高兴地说：“好，明天就去报名吧！我这文文静静的女儿终于肯动一动了。”我知道，这是妈妈所盼望的。

(9)

式中，σx、σy为x、y方向上的正应力；τxy、τyz、τxz为三向剪应力；σs为轧件材料的流变应力。

假设轧辊与轧件间摩擦为黏摩擦，在变形区上下接触面的剪切应力将达到最大值，即

(10)

式中，k2为下表面剪切变形抗力。

综上所述，将任务打包[10]发布可以让会员同时接到多个由公司设计好的最优任务包，能够让会员在最短的时间内完成较多的任务．并且将任务打包发布可以将单个任务价格适当调低，既能保证会员的收入又能减少公司的费用．通过对原定价模型的修改使一些“冷门”任务得以完成，将任务的执行情况进行了优化，提高了任务的完成度．

因此，轧件上下两部分屈服条件为

(11)

(2)半河岸半河床段水面线(旱季)以上开挖(尾水渠前1.6km和后0.8km)。水面线以上开挖，沿水流方向逆向进行分段进行施工，分2层进行，第1层为土石分界线～弱风化，第2层为弱风化至河床大面以下2m(用于导水)。

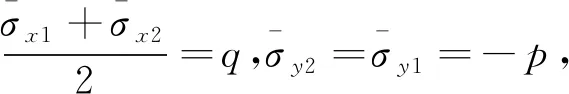
(12)

将式(12)和式(8)代入式(6)，可得

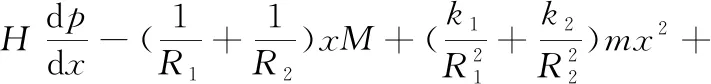
(13)

解上式微分方程，可得

(14)

在入口处，x=L，q=0，代入式(12)可得

(15)

由此计算出C1的值：

那么，在Ⅰ区受到的单位轧制力为式(15)解得的p。

在前滑Ⅲ区，单位体受力情况如图4c所示，由于咬入角比较小，故单元体在水平方向和垂直方向的受力平衡方程为

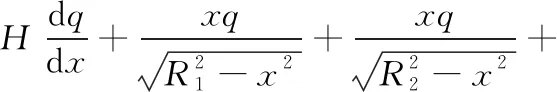
(16)

p1-τ1tanθ1=p2-τ2tanθ2=p

(17)

整理可得

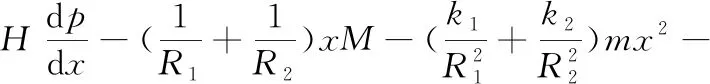
解上式微分方程，可得

数学是一门运动、变化着的科学，其很多知识点都是发现一种运动的数学规律，或者是用运动规律来表示数字之间的关系，这也是对函数最简单、直接的解释。在传统教学中，教师很难处理和展现数学的运动性，只能简单地给学生看静态的数学，导致在解决动态问题时，非常吃力。信息技术的出现，突破了这一教学方法所运用技术的瓶颈，产生了新的教学方案。如学习“动点”的轨迹，原本教师只能在黑板上“笨拙”地画出几个点，学生勉强明白。现在，教师可以利用信息技术来处理数字信息，整合为图像，画出更多的轨迹变化，学生既能看到运动的结果，也能看到运动的过程。如此直观的演示，对学生研究动态运动方程非常有帮助。

(18)

在变形区出口处，x=0，q=0，代入式(12)可得

(19)

那么，在Ⅲ区受到的单位轧制力为式(23)解得的p。

那么，在Ⅱ区受到的单位轧制力为式(19)解得的p。

在搓轧区，单位体受力情况如图4b所示，由于咬入角比较小，故单元体在水平方向和垂直方向的受力平衡方程为

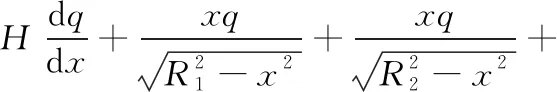
(20)

p1-τ1tanθ1=p2+τ2tanθ2=p

(21)

整理可得

(22)

解上式微分方程，可得

(23)

由于单位轧制力在上中性点xn1和下中性点xn2处是连续的，故有：

pⅠ(x=xn1)=pⅡ(x=xn1)
pⅡ(x=xn2)=pⅢ(x=xn2)

联立可求出C3。

由此计算出C2的值为

②考虑需求方特征——企业是否亏损。如表中第二列和第三列回归系数所示，分组检验发现：亏损企业组，审计定价与企业内控缺陷虽然存在正相关关系，却不显著；盈利企业组，审计定价与企业内控缺陷存在正相关关系，在1%水平上显著。即其他条件相同时，与亏损企业相比，盈利企业存在内控缺陷时的审计定价更高，H2得到验证。从全样本回归中可以看出，企业是否亏损对应的回归系数是0.058，在1%水平上显著，这说明其他条件不变时，盈利企业相比亏损企业审计定价较低。

以上计算得到的为大型锥形筒节某一层的单位轧制力分布，单位轧制力随着大型锥形筒节的宽度系数e的变化而变化。

那么总轧制力为在接触弧长和宽度方向上的定积分：

进而根据式(5)可求得轧辊施加到筒节的总轧制力。

本奥多·W·舒尔茨在1987年的《改造传统农业》著作中，将农业分为传统农业、现代农业和过渡农业等三大类。传统农业的生产要素供给和技术水平不变，整个产业部门是完全竞争的状态，均衡价格恒定。传统农业由于劳动效率和资本收益率偏低，无法吸引更多的劳动力和资本等要素流入，长期处于低水平均衡状态。在传统农业向现代农业转变过程中，要求农业从低效率、低资本收益的部门向高生产效率、高资本收益的部门转变，需要引进新的农业现代化因素，投入新的生产要素和实施新技术，更需要对农民投资，提升农民劳动力素质和组织化程度。

其中，在Ⅰ区和Ⅲ区，c=1，在Ⅱ区，c=2。

2 锥形筒节轧制过程有限元计算模型

由于大型锥形筒节轧制初期理论研究还不成熟，故ABAQUS有限元模拟是一种较好的选择。ABAQUS有限元模拟具有较高的精度和可信度，在进行实际的实验生产之前进行有限元模拟，可以提前模拟实际轧制的情况，预知轧制可能出现的问题，大大节省时间和成本。本文以某接管段锥形筒节轧制成形为例，采用的材料是2.25Cr1Mo0.25V，其基本参数通过实验测定，如表1所示。

传统加工过程需要经过5个工序：下料、镦冲、芯棒拔长、马杠扩孔和最终成形。本文研究的轧制坯料来自扩孔后的锻件，且坯料锥度与目标尺寸相同。本文基于有限元软件，建立大型锥形筒节轧制过程有限元模型，如图5所示，轧辊简化为刚体，包括外辊、芯辊、宽展辊、支承辊。外辊和芯辊为锥形辊，锥度和筒节目标锥度一致，外辊和芯辊为主动辊，芯辊同时承担道次压下功能，芯辊和外辊的转速要与轧辊直径和轧件尺寸匹配，道次压下量根据产品而定，防止筒节受力不均，变形严重；宽展辊为从动辊，控制锥形筒节宽度，由于轧制过程中锥形筒节径向速度不同，所以宽展辊设计为锥形辊，与锥形筒节径向速度分布一致，可

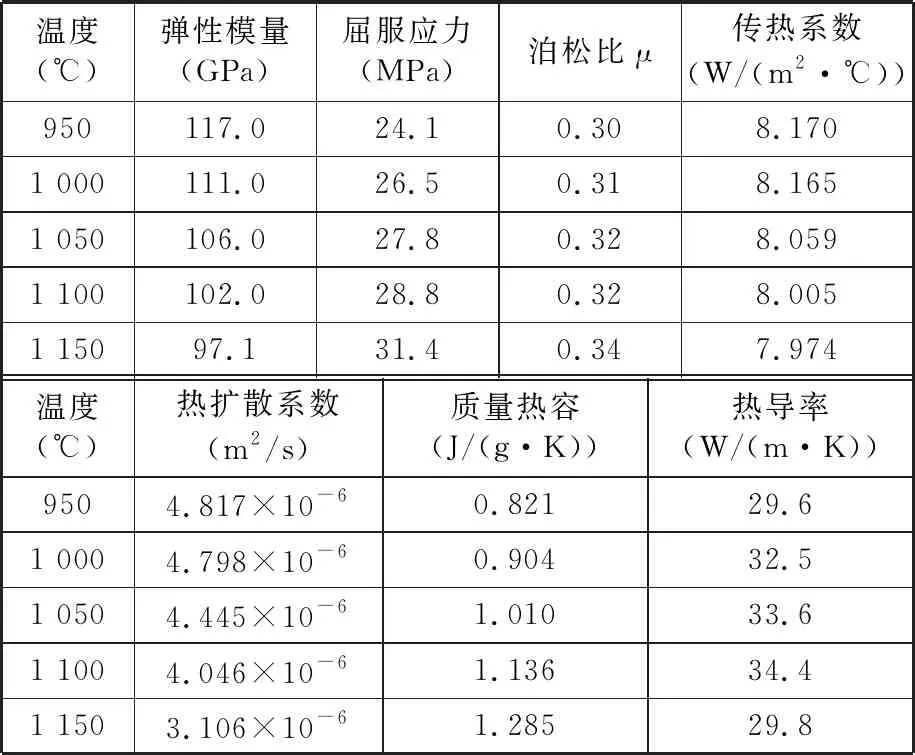
表1 有限元模型材料参数

以减小宽展辊的磨损；支承辊承受锥形筒节自重及轴向力，因此设计多个支撑辊共同支撑。锥形筒节初始温度为1 100 ℃，轧制过程主要有辐射传热和接触换热。辐射传热主要是锥形筒节向周围环境进行热辐射，定义辐射换热系数；接触换热主要是在轧辊与锥形筒节之间的热传导，另外还存在摩擦热，定义摩擦因数以及法向硬接触[26]。由于锥形筒节尺寸巨大，既要保证计算精度，又要保证计算成本，所以本文采用质量缩放来加快计算速度[27]。建模参数如表2所示。

图5 有限元几何模型Fig.5 Finite element geometric model

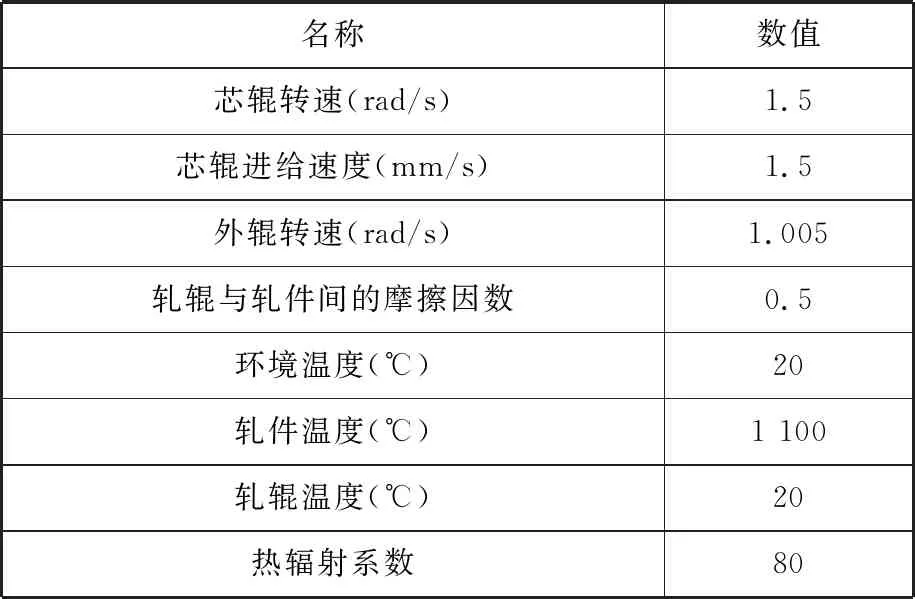
名称数值芯辊转速(rad/s)1.5芯辊进给速度(mm/s)1.5外辊转速(rad/s)1.005轧辊与轧件间的摩擦因数0.5环境温度(℃)20轧件温度(℃)1 100轧辊温度(℃)20热辐射系数80

3 结果分析与讨论

以某锥形筒节为研究对象，选取不同规格大型锥形筒节在不同条件下的轧制作为计算算例，表3为大型锥形筒节轧制主要设备参数，表4给出不同轧制条件下力学模型计算和有限元模拟计算总轧制力结果对比，保持芯辊转速为1.5 rad/s，进给速度为1.5 mm/s，外辊转速与之匹配。由表4可知，力学模型计算结果和ABAQUS有限元模拟计算结果误差在20%以内，间接表明理论模型计算与有限元计算结果的准确性，能够满足工业应用要求。

经过多年的对往复式压缩机、离心式压缩机、汽轮机等转动设备转子轴断裂前期振动状态监测、各类振动信号分析对比，发现采用不同的监测方式和不同的传感器信号对监测诊断转子轴的裂纹发展趋势的效果有很大区别，有的监测在转子轴断裂数天前也没有明显异常，而另外的监测结果是在转子轴断裂数天前振动信号就出现异常趋势，情况不一，很难准确判断。

“点破朦胧，笔画朱砂”,随着音乐响起，李校长和嘉宾以及班主任老师端起朱砂，手执毛笔，在同学们额头正中点上红痣，祝福学生们从此眼亮心明。

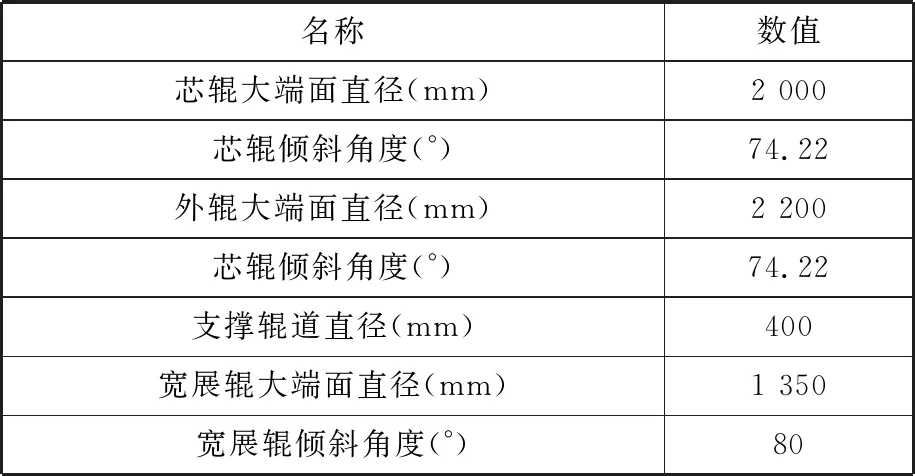
表3 大型锥形筒节轧制主要设备参数

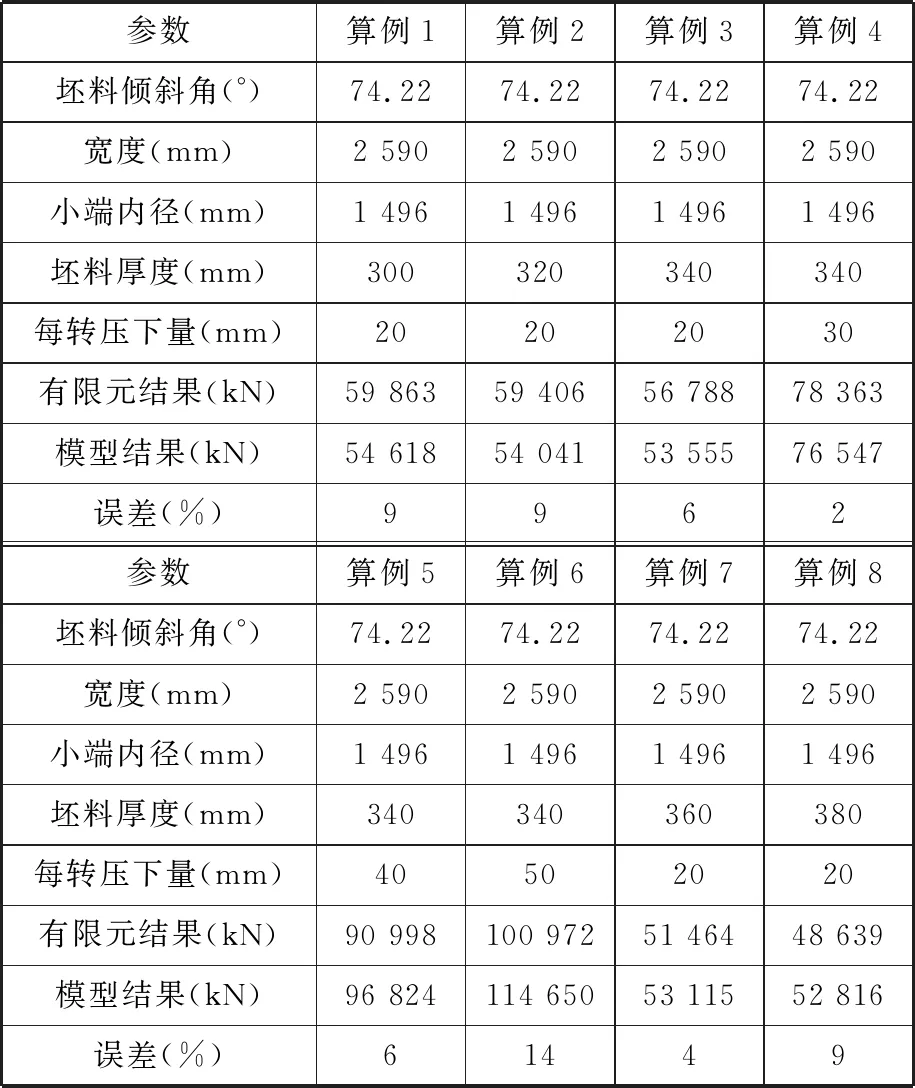
表4 力学模型计算和有限元模拟计算结果对比

图6是不同压下量时力学模型计算总轧制力和有限元模拟计算的总轧制力的对比图。由图6可知，每转压下量由20 mm增加到60 mm时，总轧制力力学模型计算结果由53 555 kN增加到129 600 kN，ABAQUS有限元模拟计算结果由56 788 kN增大到108 390 kN，两者变化趋势相同，都呈现增大趋势。ABAQUS有限元模拟计算总轧制力变化存在波动，这与网格划分有一定的关系，并且误差在允许范围之内。力学模型和ABAQUS有限元模拟计算结果误差保持在20%以内，并且在实际轧制过程中轧制力是随着每转压下量增大而增大，从而可以相互印证本文所建立的轧制力力学模型与有限元轧制模型的正确性。

统一战线在构建共同体中作出了重要贡献。统一战线对构建共同体的贡献，在横向上体现在统一战线五个主要领域之中，在纵向上体现在统一战线的具体形态之中，在层次上体现在共同体的演进之中。中国统一战线构建的共同体是拥有领导核心、紧密团结、包容开放、稳定高效的共同体。这种共同体是以中国共产党为领导核心，以马克思主义及其中国化成果为理论指导，以中国特色社会主义制度为保障，以中华民族伟大复兴为最大公约数，以正确处理一致性和多样性关系为基本方针，以求同存异、合作共赢为基本理念，致力实现利益均衡、有序稳定、认同增进的同心圆式共同体。统一战线对共同体思想的运用及其成果主要体现在以下三个方面：

通过本次研究，发现目前国内ESP课程研究尚不够完善：学生需求分析尚不够全面；ESP教学以阅读和翻译为主，忽略了听说能力的训练；教学目标不够具体，教学方法及教学手段陈旧。依据本次问卷调查的结果以及以往研究的结论，笔者认为，现阶段大学英语教学改革应将重点转移到课程内容设置的问题上来，具体探讨大学阶段ESP课程的设置问题[7]。具体提出以下几点建议。

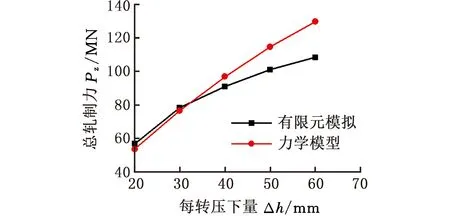
图6 总轧制力随每转压下量的变化Fig.6 Change of total rolling force with reductionper rotary pressure

图7是不同厚度、相同压下量情况下，力学模型和有限元模拟计算结果对比图。由图7可知，在轧制过程中，大型锥形坯料厚度由300 mm增大到380 mm时，总轧制力力学模型计算结果由54 618 kN减小到52 816 kN，ABAQUS有限元模拟计算结果由59 863 kN减小到48 639 kN，两者变化趋势相同，都呈现降低趋势，同样ABAQUS有限元模拟计算总轧制力变化存在波动，但误差在允许范围之内。力学模型和ABAQUS有限元模拟总轧制力计算结果误差保持在20%以内，并且在实际轧制过程中轧制力是随着坯料厚度增大而减小，从而可以相互印证本文所建立的轧制力力学模型与有限元轧制模型的正确性。

图7 总轧制力随筒节厚度的变化Fig.7 The variation of total rolling force with thethickness of barrel joint

图8 力学模型单位轧制力分布Fig.8 Mechanical model unit rolling force distribution

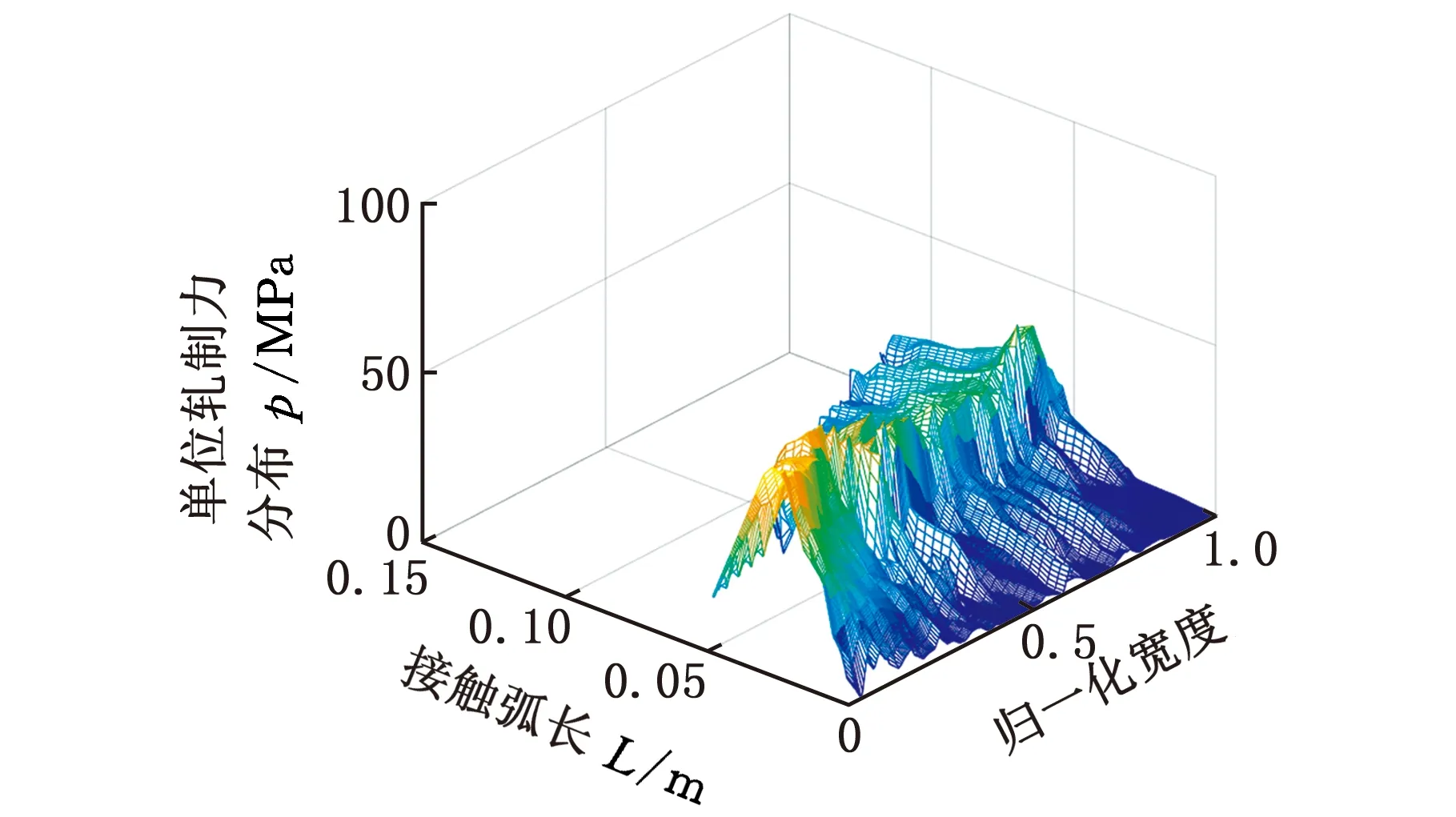
图9 有限元模拟单位轧制力分布Fig.9 Finite element simulation of rolling forcedistribution per unit

图8所示是采用轧制力力学模型计算的大型锥形筒节轧制变形区单位轧制力分布。图9所示是采用ABAQUS有限元模拟得到的轧制变形区单位轧制力分布。由图8和图9可知，模型计算结果和有限元计算结果总体变化趋势是一致的，单位轧制力在宽度方向上由锥形筒节小端到大端逐渐减小，小端面最大单位轧制力在98 MPa左右，大端面最大单位单位轧制力为62 MPa左右；接触弧长从小端到大端逐渐增大，最小端接触弧长在0.6 m左右，最大的接触弧长在0.11 m左右。在轧制变形区沿接触弧方向上单位轧制压力先增大后减小，在搓轧区轧制力变化平缓，最大单位轧制压力出现在靠近出口端的后滑区。

选取力学模型和有限元模型同一位置层，进行单位轧制力对比，如图10所示。两者单位轧制力分布趋势基本一致，最大单位轧制力均为靠近出口端的后滑区和搓轧区，单位轧制力力学模型为100 MPa，有限元模型为103 MPa，有较小的误差，说明所建立的力学模型与有限元计算模型有较高的精度。

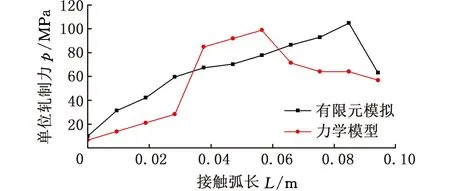
图10 接触弧长方向单位轧制力Fig.10 Unit rolling force distribution in contact arclength direction

图11所示是不同芯辊和外辊转速比下的总轧制力。由图11可知，当n2/n1<1.25和n2/n1>1.6时，力学模型与有限元模拟计算结果误差较大，有限元计算结果波动范围大，说明该范围内轧制过程稳定性差、轧制失稳；当1.25

图11 不同芯辊和外辊转速比下的总轧制力对比Fig.11 Comparison of total rolling force underdifferent rotational speed ratios of core roll toouter roll

4 结论

本文针对大型锥形筒节轧制过程，提出一种微分分层方法，结合主应力法，建立了大型锥形筒节轧制过程轧制力力学模型，计算得到了大型锥形筒节总轧制力的计算公式以及变形区轧制力分布状态；同时在目前无法进行实验的条件下采用ABAQUS有限元模拟大型锥形筒节轧制过程，对比分析计算结果，力学模型计算结果与有限元仿真结果误差在20%以内，有较高的精度；根据力学模型和有限元计算结果分析了大型锥形筒节轧制变形区单位轧制力三维分布规律，单位轧制力在宽度方向上由锥形筒节小端到大端逐渐减小，接触弧长从小端到大端逐渐增大，在轧制变形区沿接触弧方向上单位轧制压力先增大后减小，在搓轧区轧制力变化平缓，最大单位轧制压力出现在靠近出口端的后滑区；在有限元模拟的基础上进行芯辊与外辊转速比对轧制力和轧制稳定性的影响研究，得出保证锥形筒节轧制稳定运行的转速比范围区间为1.25～1.60。