断裂准则对TC4钛合金板抗卵形头弹冲击的影响
2019-10-25邓云飞张伟岐徐美健王陆军
邓云飞 张 永 张伟岐 徐美健 王陆军
中国民航大学航空工程学院,天津,300300
0 引言
TC4合金是一种中强度钛合金,既有较高的强度,又有较高的塑性,能长期在高温环境下工作,在航空、航天、船舶、化工以及兵器领域得到非常广泛的应用[1]。数值模拟是预测材料延性失效破坏的一种不可或缺的方法,虽然过去十几年中对材料延性失效的研究从未间断,但目前仍然没有一个“通用”标准能够准确评估材料延性失效相关的所有问题[2]。诸多文献以多种方式将材料等效应变、绝热温升、应变率效应和应力三轴度考虑到弹靶冲击或Taylor杆撞击的数值模拟中,预报靶或弹的断裂行为,虽然数值模拟能获得与试验接近的预测结果,但本构模型与断裂准则对数值模拟计算的影响仍然需要进一步的研究[3-5]。GIGLIO等[6]利用Ti-6Al-4V材料,采用试验与数值模拟结合的方法对B-W断裂准则进行校验,并且研究了应力三轴度对材料失效应变的影响。NIMA等[7]利用Ti-6Al-4V材料进行了光滑圆棒与缺口圆棒准静态拉伸试验,对断裂应变与应力三轴度和Lode角两者同时相关的Modified Mohr-Coulomb(MMC)、连续损伤演化的CDM断裂准则进行参数标定,以研究不同应力状态下材料的断裂机制。陈刚[8]通过TC4钛合金材料动态力学性能试验,分别采用Johnson-Cook (J-C) 和H-M断裂准则研究失效应变随应力三轴度的变化,结果表明,H-M断裂准则能更合理地预测失效应变随应力三轴度的变化关系。
基于国内外研究现状分析,本文采用基本的J-C、分段式H-M和引入Lode角的MMC断裂准则,进行TC4钛合金靶板抗卵形头弹冲击的数值模拟研究,并将模拟结果与试验进行对比,揭示断裂准则对靶体冲击失效特性数值模拟的影响。
1 试验过程及结果分析
1.1 试验概况
利用中国民航大学一级气炮进行弹靶撞击试验。靶板厚度为2 mm,边长为200 mm×200 mm,靶体周向加工有8个螺栓孔。弹体由经过热处理的38CrSi合金钢加工而成,硬度为53HRC,直径为12.68 mm,名义质量为34.89 g,弹体的几何外形及参数如图1所示。
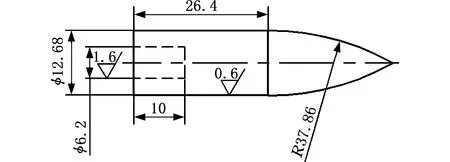
图1 卵形头弹体形状及尺寸Fig.1 Geometry of the ogival-nosed projectiles
1.2 弹道极限
利用卵形头弹体对靶体进行6次有效正撞击试验,结果如表1所示。

表1 试验结果
利用RECHT等[9]提出的弹道极限公式(R-I公式)进行计算,其表达式如下:
(1)
式中,a、p为模型参数;vi、vr与vbl分别为初始速度、剩余速度及弹道极限速度。
利用最小二乘法对弹体的初始-剩余速度进行拟合,如图2所示。弹体的弹道极限速度为128.5 m/s。
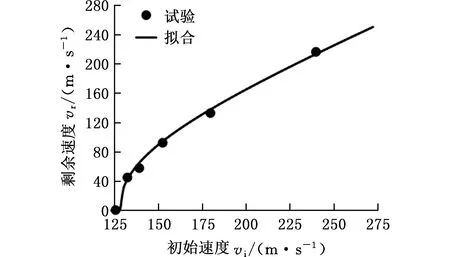
图2 弹体初始-剩余速度曲线Fig.2 Initial vs. residual velocity curves of projectiles
1.3 靶体延性失效模式
利用高速摄像机观察弹体撞击靶板的过程,如图3所示。弹体在击穿靶板前后保持良好飞行姿态。靶板在整个撞击过程中产生明显的局部变形,伴随有少量的碎屑产生。
弹体高速正撞击靶板,靶板产生局部延性失效破坏,如图4所示。靶板的主要失效模式是花瓣开裂,还有一定程度的局部盘式隆起。靶体受卵形头弹撞击而承受张力,当达到靶板材料的拉伸极限强度时,靶板在高的轴向和环向拉伸应力的作用下,产生一定的结构变形和呈现接近直角的花瓣开裂。靶体在花瓣开裂的根部有一定数量的裂纹产生,呈现出一定程度的延性伸长与脆性撕裂特征。

(a)vi=125.9 m/s,vr=0

(b)vi=240 m/s,vr=216.3 m/s图3 卵形头体弹撞击靶板的过程Fig.3 The process of plate impact s by ogival-nosed projectile

(a)vi =139.4 m/s

(b)vi =240.0 m/s图4 靶板失效模式Fig.4 Failure modes of plates
2 弹体撞击靶体数值模拟结果分析
2.1 建立数值计算模型
利用ABAQUS/Explicit建立三维有限元模型,弹体材料与模型见文献[10],设为刚性体,采用均匀化网格划分,网格尺寸为1 mm×1 mm×1 mm。靶板均采用直径为180 mm的圆形板,并且对靶板的边界进行刚性约束,如图5所示。为缩短计算时间,靶板网格划分为中心撞击区域和边界区域,中间采用过渡区,中心区域网格尺寸为0.2 mm×0.2 mm×0.2 mm。由于弹体与靶板撞击接触过程存在摩擦作用,因此在接触中设置摩擦因数为0.1。
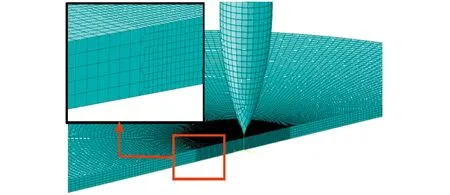
图5 弹靶有限元模型Fig.5 The finite element mode of targetand projectile
2.2 本构模型及断裂准则分析
靶板采用J-C本构模型[11],材料von Mises等效应力σeq为
(2)
T*= (T-Tr) / (Tm-Tr)
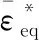
数值模拟中,断裂标准采用线性损伤演化[12],损伤变量定义为
D=∑Δεeq/εf
(3)
式中,Δεeq为等效塑性应变增量;εf为材料断裂应变。
当损伤变量D达到1时,删除该单元。
断裂准则中断裂应变通常与应力状态、应变率和温度有关,表达式为
(4)
η=σm/σeq=(σ1+σ2+σ3)/(3σeq)
(5)
(6)
(7)
(8)
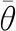
为方便工程应用,通常将应力状态、温度及应变率对断裂应变的影响分开考虑[11],即
(9)
若不考虑Lode角参数影响(如J-C断裂准则),则断裂应变定义为
(10)
式中,D1~D5为材料性能参数。
陈刚[8]通过一系列材料力学性能测试,采用分段函数描述TC4钛合金断裂应变随应力三轴度变化关系。当η>1/3和η<0时,分别采用H-M断裂模型描述,二者之间部分采用线性拟合表达两种模式的共同作用,表达式如下:
(11)
式中,C1~C5为材料性能参数。
同时考虑应力三轴度、应变率效应和温度效应后,H-M断裂准则定义为
(12)
NIMA等[7]对钛合金材料进行一系列不同应力状态的力学性能试验发现,钛合金材料的失效应变不仅与应力三轴度相关,而且与Lode角参数相关,因此应采用MMC准则,该准则含应力三轴度和Lode角参数影响,不含温度及应变率效应。对MMC断裂准则进行参数标定,表达式如下:
(13)
式中,APL、nF为塑性硬化参数;K1、K2、K3为材料性能参数;α为修正系数,0<α≤1。
2.3 确定MMC准则修正系数α值
采用文献[7]所使用的MMC断裂准则,并引用其参数。利用不带修正系数的MMC断裂准则进行弹体撞击TC4钛合金靶板数值模拟,对比数值模拟与试验结果,发现MMC准则高估了TC4钛合金材料的延性。因此,采用修正系数α降低材料的断裂应变,如式(13) 所示。材料参数如表2所示[7-8,12]。
采用带有修正系数α的MMC断裂准则,得到弹体的初始与剩余速度,并利用R-I公式进行拟合,结果如图6所示,此外,不同修正系数下的弹道极限速度如表3所示。弹道极限速度随修正
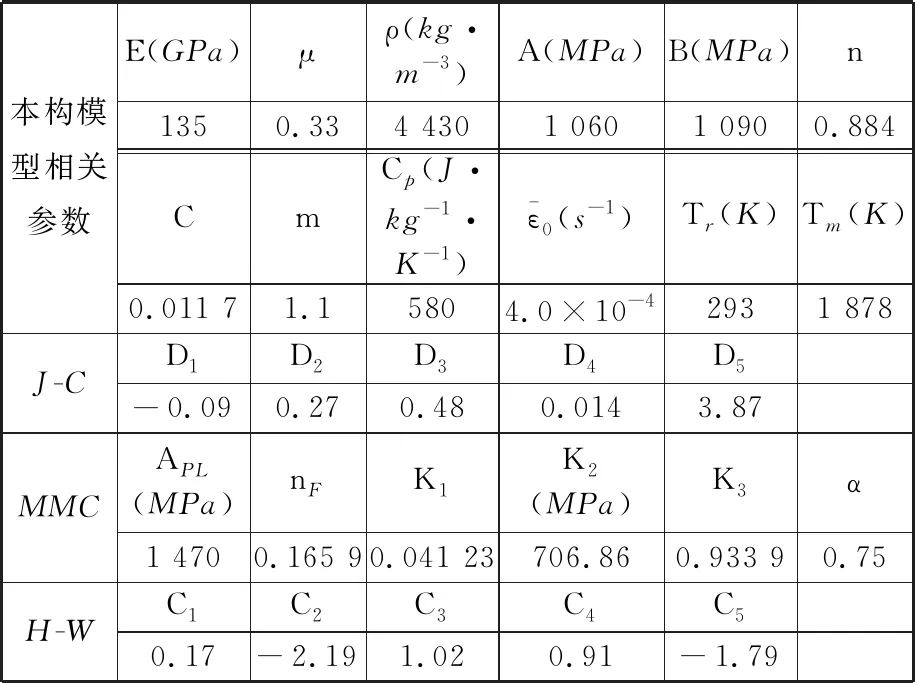
表2 钛合金材料参数
系数α的增大而显著增加,当修正系数α小于0.75时,数值模拟的弹道极限速度与试验比较接近。
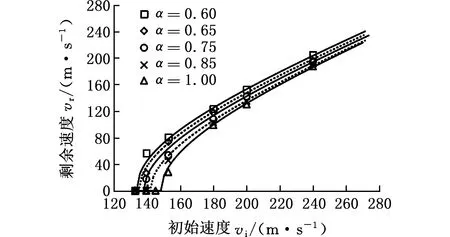
图6 不同修正系数α时MMC准则预报的弹体速度Fig.6 Velocity of the projectiles predicted by theMMC criterion under different correction factors α

α0.600.650.750.851.00弹道极限速度vbl(m·s-1)133.6134.9137.8141.7148.2

(a)试验 (b)α=0.60 (c)α=0.65
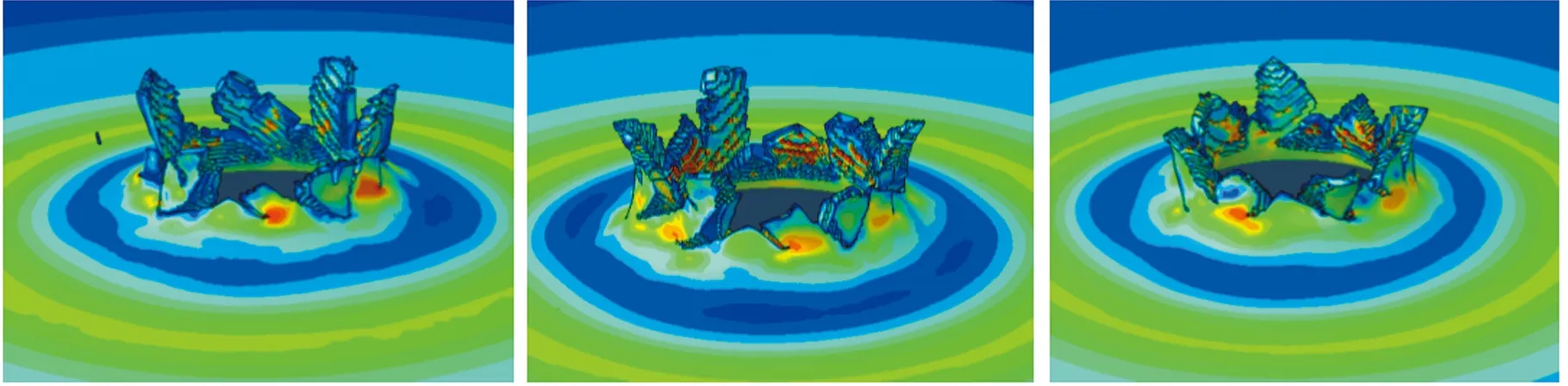
(d)α=0.75 (e)α=0.85 (f) α=1.00图7 MMC准则预测的靶板失效模式Fig.7 Failure mode of plate predicted by MMC criterion
图7所示为弹体撞击速度为240 m/s时,不同修正系数MMC准则预测的靶体失效模式。当α值分别为0.60、0.65、0.75、0.85和1.00时,MMC准则预测的靶板开裂花瓣数量分别为8、10、9、10和9,而试验的花瓣数量为8。数值模拟预测的靶板延性随着α值增大而增大,当α小于0.75时,靶板主要表现为脆性断裂,MMC准则低估了材料的延性;α>0.75时,靶板主要表现为延性断裂,MMC准则高估了材料的延性;α=0.75时,MMC准则预测的靶板开裂花瓣数量、变形形状和延性失效破坏均与试验最接近,并且弹道极限也接近于试验结果。因此,MMC断裂准则修正系数α取值为0.75。
2.4 弹道极限
利用不同断裂准则进行弹体撞击靶体数值模拟,计算得到弹体的初始-剩余速度,并使用式(1)进行拟合,结果如图8和表4所示。J-C准则预测结果低于试验结果约10.5%。H-M准则预测结果与试验几乎一样,而MMC准则预测结果高于试验结果约7.2%。因此,H-M准则预测结果与试验最吻合。
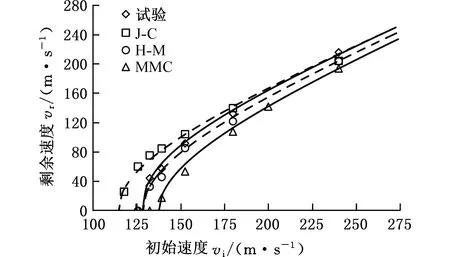
图8 试验与数值模拟的弹体初始-剩余速度曲线Fig.8 Initial vs.residual velocity curves of projectiles for numerical simulation and test

表4 试验与数值模拟的弹道极限
2.5 靶板失效模式
弹体撞击速度为139.4 m/s与240 m/s时,试验与数值模拟的靶板失效破坏模式对比如图9所示。当弹体低速撞击靶板时,TC4钛合金靶板均产生局部变形及花瓣开裂。J-C、H-M和MMC断裂准则预测的靶板开裂花瓣数量分别为4、5和5,试验花瓣数量为4,3种断裂准则预测的靶板花瓣数量均与试验接近。从靶板局部变形、花瓣开裂和断口特征分析,J-C断裂准则明显低估了材料的延性,而H-M和MMC断裂准则预测的结果与试验较吻合,尤其H-M断裂准则。此外,弹体高速撞击靶板时,TC4钛合金靶板局部变形与花瓣开裂形状更显著。J-C、H-M和MMC断裂准则预测的靶板开裂花瓣数量分别为10、9和9,试验花瓣数量为8,数值模拟结果均与试验接近。不过,H-M断裂准则预测靶板失效模式最接近试验。

vi(m/s)试验J-CH-MMMC139.4240.0
图9 卵形头弹撞击靶板失效破坏模式
Fig.9 Failure and damage mode of plate impacted the ogival-nosed projectiles
2.6 靶板失效机理
综上所述,H-M断裂准则预测结果最接近试验结果,所以采用H-M断裂准则分析靶板被弹体撞击的失效机理。弹体撞击靶板时,靶板裂纹均首先从其背面产生,随撞击过程的进行,花瓣开裂数量增加、局部盘式隆起明显、裂纹长度显著增加,如图10所示。
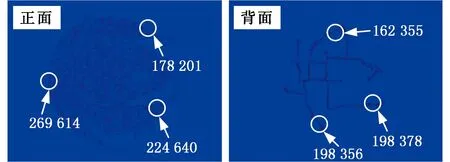
提取靶板典型失效单元,计算并分析历程信息,如损伤变量D、应力三轴度η。图11所示为弹体撞击速度分别为139.4 m/s和240.0 m/s时,靶板正面和背面的损伤裂纹;图12与图13所示分别为从靶板正面和背面提取的典型失效单元信息,典型失效单元从损伤裂纹处提取。图11~图13中数字为数值仿真中靶板的单元号。由图12与图13可以看出,弹体低速撞击时,靶板正面失效单元应力三轴度均为正值,而靶板背面失效单元在200 μs之前均为正值,200 μs之后均为负值,说明靶板正面静水压力以拉伸为主,背面静水压力先以拉伸为主后以压缩为主。弹体高速撞击时,靶板失效单元应力三轴度变化趋势基本与低速撞击时相似,但是,弹体高速撞击时,靶板正面和背面失效单元的应力三轴度变化范围分别为0.2~0.8、-0.6~-0.2。弹体低速撞击时,应力三轴度分别在0~0.6、-0.4~0之间,这说明靶板单元无论以拉伸为主还是以压缩为主,高速撞击的靶板静水压力均大于低速撞击的靶板静水压力。
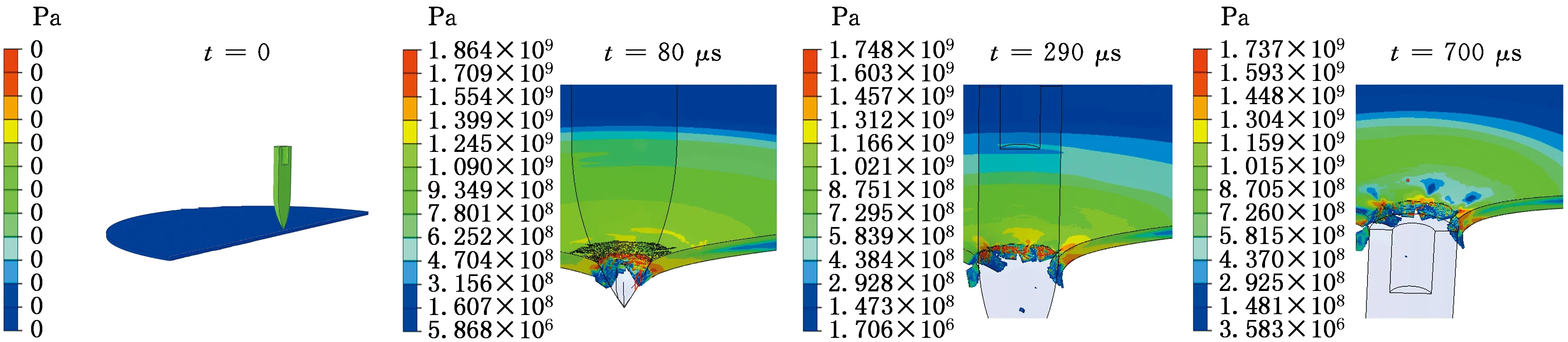
(a)vi=139.4 m/s
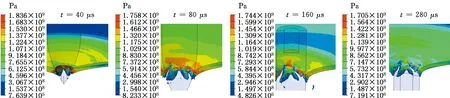
(b)vi=240.0 m/s图10 数值模拟卵形头弹撞击过程Fig.10 Impact process of the ogival-nosed projectiles for numerical simulation
(a)vi=139.4 m/s

(b)vi=240.0 m/s
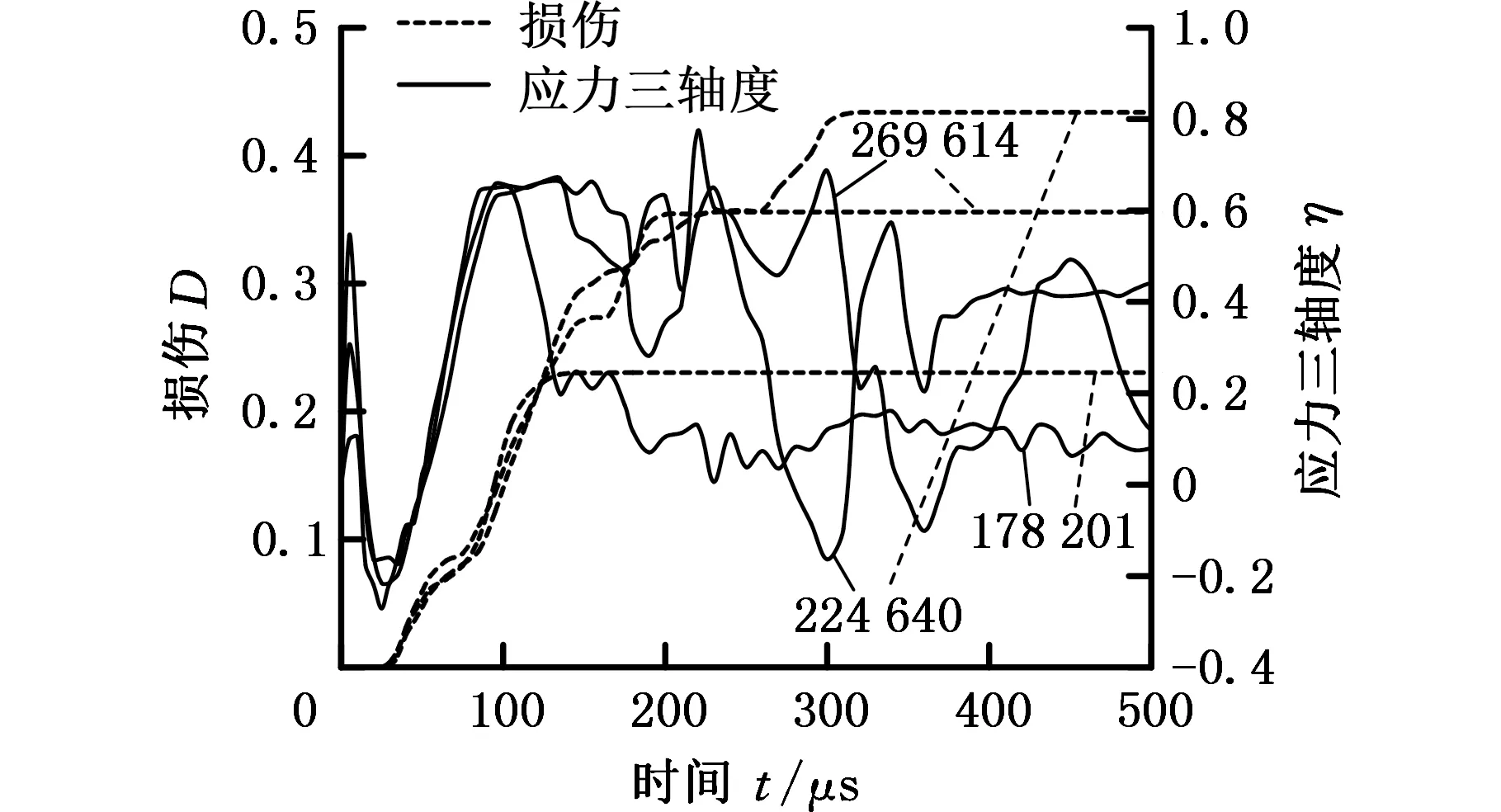
(a)靶板正面失效单元

(b)靶板背面失效单元图12 靶板典型单元失效信息(vi=139.4 m/s)Fig.12 History plots for typical failed element(vi=139.4 m/s)
3 结论
(1)采用J-C、分段式H-M和MMC断裂准则进行弹体冲击靶体数值模拟计算,对比分析靶板的弹道极限速度及失效模式,揭示断裂准则对TC4钛合金靶板撞击失效特性数值模拟的影响。
(2) H-M与MMC准则预测的靶板失效模式与试验比较一致,能够合理地反映材料的延性,而J-C准则预测结果与试验相差比较大。从弹道极限速度和失效破坏模式综合考虑,H-M准则预测的结果与试验最接近,可准确描述失效应变随应力三轴度的变化关系,能提高数值模拟预测结果的精度。
(3)MMC断裂准则高估了材料的延性,采用合理的修正系数α可以降低断裂应变,在数值模拟中Lode角参数存在明显的影响。
(4)在弹体不同速度撞击下,靶板正面与背面典型失效单元的应力三轴度变化趋势基本一致,靶板正面静水压力以拉伸为主,背面静水压力从以拉伸为主转变为以压缩为主。
