借助I-U图像深度探究△U·△I与△P的关系

曹 宏，张善贤

1.苏州工业园区教师发展中心，江苏 苏州 215021

2.苏州市吴中区教研室，江苏 苏州 215121

1 问题的缘起

在考查简单串联电路中电功率问题的初中物理试卷中，经常会涉及到这样一类问题：当用电器在电压发生变化时，比较电功率的变化量△P与其电压变化量△U、电流变化量△I的乘积△U·△I的大小关系。例如，2018年河北省中考物理试卷第15题，此题中C选项就是对简单串联电路中定值电阻△U·△I与△P的大小进行比较的问题。

试题如图1所示，电源电压不变，a、b、c为电流表或电压表，只闭合S1时，a表无示数，b表有示数。S1、S2都闭合时，滑片P向右滑动，c表的示数不变，下列判断正确的是（ ）

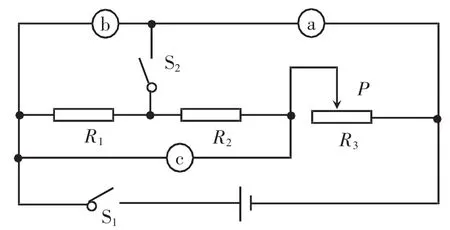
图1 试题示意图

A．a表是电压表

B．先闭合S1，再闭合S2，电路中的总电流变大

C．只闭合S1，P向右移动，R2两端的电压变化量与电流变化量的乘积大于其电功率的变化量

D．开关均闭合，电路的总功率为P1，若将c表换成另一种电表，再闭合S1、S2，电路的总功率为 P2，则 P2>P1

剖析本题中C选项的电路特点，可以归结为如图2所示的基本电路模型。图2中R1为定值电阻，R2为滑动变阻器，闭合S，滑片P右移至某位置时，记录两表的示数分别为U1、I1，继续将P右移到另一位置时，两表示数增至U2、I2。

图2 基本电路模型

易得△U=U2-U1，△I=I2-I1

定值电阻R的电功率增量

显然，△P>△U·△I，即定值电阻电功率的增量△P大于其两端电压的增量△U跟通过电流的增量△I的乘积。

对上述推导过程，也可沿以下思路展开：

上式不能直接看出△P>△U·△I，但经过换算后也应该能得到结论。

在解决简单电路有关电流、电压、电阻、电功率等各物理量的问题时，用电器的电流I与电压U的关系图像（I-U图像）是一个重要的工具，它具有信息量丰富、直观方便的特点[1]。为此，本文拟采用I-U图像为研究工具，深度探究在简单串联电路中定值电阻、可变电阻、总电路的△U·△I与△P具有怎样的关系，为初中物理教学提供参考。

2 用I-U图像研究△U·△I和△P的关系

2.1 定值电阻的△U·△I和△P的关系

1．图像对关系式的验证

图3是图2所示电路中定值电阻R1的I-U图像。当电压从U1增至U2时，对应的电流由I1增至I2，电功率增量△P就是图中矩形OU2O3I2的面积与矩形OU1O1I1的面积之差，即图中阴影部分的面积S（以下简称“7”形面积）。而△U·△I的值就是图中O1O2O3O4部分所围成的面积S1。显然S>S1，说明了由公式推导出的△P>△U·△I结论的正确性。

图3 基本电路I-U图中“7”形面积

在图3中，“7”形面积由三块组成，除 S1以外，另两块为矩形I2O4O1I1部分的面积S2，矩形U1U2O2O1部分的面积S3，从图上可以看出S2=△I·U1，S3=△U·I1，S=S1+S2+S3，与（1）式中△P=△U·I1+△I·U1+△U·△I相对应。

在图3中，也可以将“7”形面积S表示为S=（S2+S1）+（S3+S1）-S1，从图上可以看出：S2+S1=△I·U2，S3+S1=△U·I2，所以有 S=△U·I2+△I·U2-△U·△I，也即与（2）式相对应。

因为S>S1，所以从（2）式同样应能得出△P>△U·△I的结论。

2．通过图像拼接实现对关系式的拓展

（1）从图 3可以将“7”形面积 S表示为 S=（S2+S1）+S3，据此可写出对应的关系式：

“7”形面积 S 还可以表示为 S=S2+（S1+S3），对应关系式

（2）△P的其他变形式

①由 S=S1+S2+S3，及 S2=S3，可得 S=S1+2S2，再由图 3 可知：S2+S1=△I·U2，

S2=△I·U1，这样有

②由 S=S1+S2+S3，及 S2=S3，可得 S=S1+2S3，再由图 3 可知：S1+S3=△U·I2，

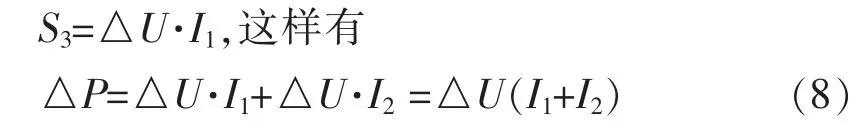
同样方法，利用（8）式以及△I=I2-I1又可以得到△P的另两种变形公式，分别为

3．几点结论

结论1：△P的10个表达式都表明了对于定值电阻而言，仅凭电压变化量△U和电流变化量△I，不能确定其电功率的变化量△P，但可以确定△U·△I一定小于△P。

结论2：△P的10个表达式都表明要计算定值电阻消耗电功率的变化率，除了△U和△I以外，还需要知道 U1、U2、I1、I2四个量中的一个，只要运用△P=U2I2-U1I1，或者中的任何一式，结合均可以导出这10个表达式。这10个表达式都可以借助于定值电阻的I-U图像中的“7”形面积的不同组合导出。

结论3：10个表达式均可以相互串联变形沟通，其中最典型的是（1）（5）（8）式，（1）式直接对应图 3 的 I-U 图像“7”形中的 S1、S2、S3，（5）（8）二式结构简明。

结论4：在电压增量△U（或电流增量△I）相同的情况下，△P的10个表达式都表明定值电阻电功率的增量△P都随电压的初始值U1的增大而同步线性增加。关于这一点也可以用图4所示的定值电阻的I-U图像加以说明。图中电压U3＞U2，I3＞I1，外侧的“7”形面积大于内侧的，两种情况下△U和△I的乘积所对应的矩形面积相等。

图4 定值电阻的I-U图

2.2 可变电阻的△U·△I和△P的关系

简单电路中的可变电阻常见的有滑动变阻器和小灯泡。

1．滑动变阻器的△U·△I和△P[2]的关系

在如图5所示电路中，电源电压为U0，定值电阻阻值为R1，滑动变阻器的最大阻值为R2。当滑动变阻器的滑片P右移时，其电压值降低，通过的电流增大，比较滑动变阻器△P与△U·△I的大小时，电压的变化量取其绝对值|△U|。为便于比较，同时作出定值电阻和滑动变阻器的I-U图像。根据滑动变阻器的最大阻值R2和定值电阻 R1的大小关系，分别作出 R2＞R1、R2=R1、R2＜R1三种情况下的I-U图像（如图6）。

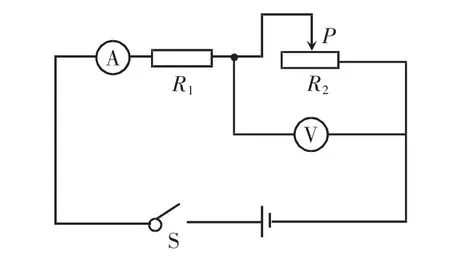
图5 含变阻器的电路

由于图6（a）能全面反映滑动变阻器电压变化导致电功率的变化情况，所以下面就以它为基准，全面分析|△U|·△I和△P的关系。

（1）图 6（a）的四个特殊坐标点

O1（U0，Im）点：当滑动变阻器的滑片移动至最右端使阻值为零时，定值电阻R1的电压为U0，电路中的电流为Im=U0/R1，此时滑动变阻器的电压和电功率均为零。O2（U0/2，Im/2）点：滑动变阻器的阻值恰好等于R1时，变阻器和定值电阻R1两端的电压均为U0/2，电路中的电流为U0/2R1，O2点就是滑动变阻器和定值电阻两者的I-U图线的交点。可论证得该点处滑动变阻器的电功率为其最大值Pm，且

O3（U1，I1）点和 O4（U1'，I1）点：当滑动变阻器的滑片移动到最左端时，其阻值为最大值R2，此时变阻器两端的电压为，定值电阻两端的电压，电流均为显然U1+U1'=U0。根据这四个坐标点，就能作出滑动变阻器和定值电阻的I-U图像。

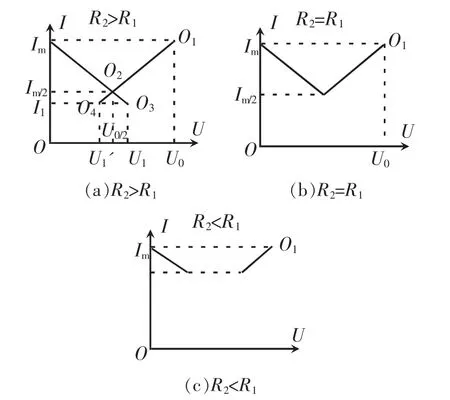
图6 不同电阻的I-U图

（2）用I-U图像显示△P[3]

假定开始时滑片处于最大阻值的位置，闭合开关后，记录滑动变阻器两端电压U1，通过的电流I1，而后移动滑片至阻值小于R1的某一位置，再记录它的电压及电流U1'、I2，如图7所示。

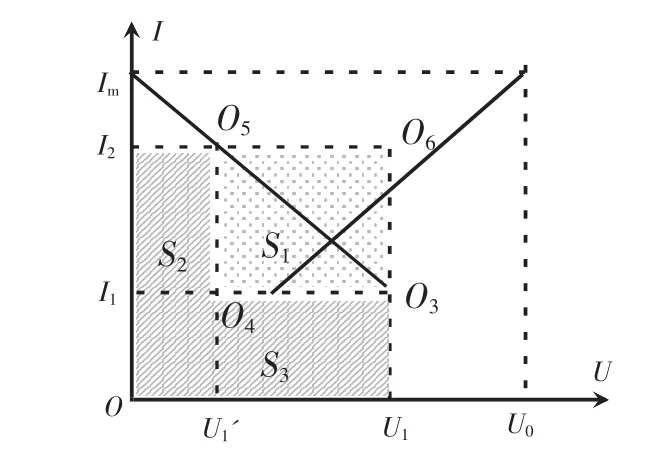
图7 变化电阻的I-U图

滑动变阻器的电功率增量△P就是图7中矩形O5U1'OI2的面积S2减去O3U1OI1的面积S3，而|△U|·△I就是矩形O3O4O5O6的面积S1，由于无法比较面积S3与S2的大小，所以表明无法判断△P的正负情况，也即无法比较△P与|△U|·△I的大小情况，这一点是滑动变阻器与定值电阻的不同之处。

但是，可以分段讨论滑动变阻器电功率的变化情况。

第1阶段，滑动变阻器由阻值最大位置R2开始，逐渐滑至阻值为R1的位置，由图8中的面积变化可以看出滑动变阻器的电功率增大，其增加的电功率△P即为矩形所围面积减去矩形O3U1OI1所围面积，由于矩形O5'O4I1Im与矩形的面积相等，所以△P即为矩形O2O4'O4O'5所围成的面积，也即△P=|△U·|△I。

图8 分段讨论电功率变化

第2阶段，滑动变阻器由阻值为R1的位置，逐渐向小于R1的某一位置滑动后，设电流恰好为I1，电压为U1'，由图8中的面积变化可以看出滑动变阻器的电功率增小，其减小的电功率△P即为矩形所围面积减去矩形OU'OI所512围面积，又由于矩形O5U'1OI2所围面积与矩形O3U1OI1所围面积相等，等同第1阶段，同样可以得到△P=|△U|·△I。

综合考虑，滑动变阻器的阻值由最大阻值位置滑至零阻值位置的过程中，滑动变阻器的电功率先增大到最大功率，再逐渐下降为零，其变化的拐点发生在阻值恰好为R1的位置。

图6（b）和图6（c）所对应的滑动变阻器电功率的变化，只存在一种情况，即当它的阻值由较大位置向较小位置变化时，电功率减小，△P为负值，借助于图8和第2阶段过程中的结论，可推证到减小量|△P|>|△U|·△I。

2.小灯泡的△U·△I和△P的关系

探究电路图如图9所示，小灯泡的I-U图像如图10所示。下面通过图像进行分析。

图9 探究电路图

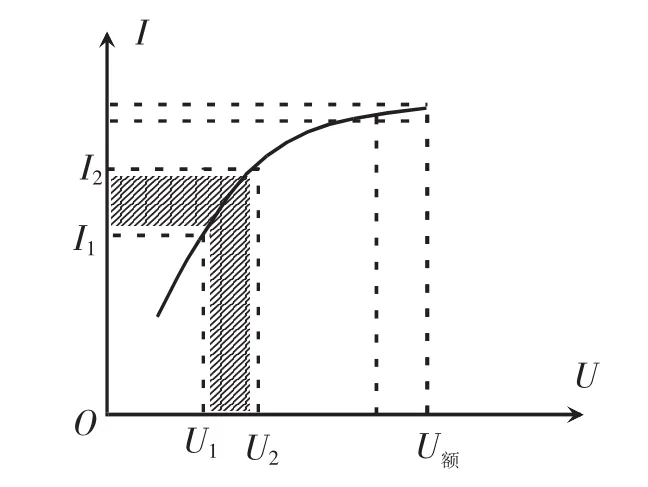
图10 探究电路I-U图

不难发现，对于△U·△I和△P，小灯泡与定值电阻在如下几个方面存在着异同：

相同点：小灯泡的电功率与定值电阻的电功率一样，随着其两端电压的增加而增大，且电功率的增量△P大于电压增量和电流增量的乘积，即△P>△U·△I。在图10所示的小灯泡的I-U图像中，小灯泡电功率的增量也如“7”形面积所示。其面积：

S=S1+S2+S3=△U·△I+△I·U1+△U·I1

不同处：

（1）因为小灯泡的灯丝电阻随温度升高而增大，所以它的I-U图像如图10所示的曲线。

（2）随着电压增大，即使△U的数值相同，但△I的数值不同，且逐渐减小，所以△U·△I的值也逐渐减小，在I-U图像中对应的矩形面积S1减小。

△P=△U·I2+△I·U2-△U·△I

△P=△U·I1+△I·U2

△P=△U·I2+△I·U1

（4）因为小灯泡通过的电流跟其两端电压的函数关系不明，所以图10所示的I-U图像只是根据I和U的数据描点而成，这样就导致小灯泡电功率的增量△P跟电压初始值的关系 （在△U相同的前提下）不明确，只能依据I-U图像粗略地估计为△P的数值先增大后减小，这是跟定值电阻的△P随电压初始值同步线性增加是完全不同的结论。