小学数学直觉思维及其培养策略

江苏省苏州市高新区实验小学校教育集团 马邹英

在当下的小学数学教学中，普遍存在着“重逻辑发展，轻直觉发展”的教学问题，影响了小学生直觉思维的发展。对数学学习者而言，直觉思维是一种不可或缺的思维能力，是他们正确认知世界，提升自己想象力与创造力的重要保障。因此，如何才能有效地发展小学生的直觉思维是当下值得深入探讨的一个重要课题。

一、小学数学直觉思维的含义与作用

小学数学直觉思维本质上是一种人类基本的思维方式，建立在一定数学知识、数学学习经验以及数学技能等基础上，通过采取联想、类比、归纳、推理、观察等方式猜想有关的数学问题，并快速做出自己的猜想与判断的能力。不同于逻辑思维，直觉思维不会受到某些逻辑规则或要求等的限制，可以对问题或事物的本质进行直接领悟的一种基本思维方式。通过培养小学生的直觉思维，有助于提高他们观察力与洞察力的基础上，进一步提升他们的直觉感知力、直觉想象力和直觉判断力，从而可以不断提高小学生的数学综合学习能力。

二、小学数学直觉思维的培养策略

1.厚积薄发，夯实数学直觉思维培养基础

数学直觉思维的培养离不开扎实的数学理论知识功底、熟练的数学基本解题技能以及丰富的数学基本活动经验等，所以为了培养与发展学生的数学直觉思维，就必须要注重积累丰富的数学知识、技能以及经验，否则无法使小学生针对数学问题形成灵感或顿悟等。直觉思维的形成固然有偶然性或随机性，但是也并非是无迹可寻的，就犹如打篮球过程中的投篮动作都是下意识的反应。如果缺乏必要的数学知识结构、知识情境或认知基础等，那么自然无法培养他们的直觉思维。因此，在平时的数学教学中，教师需要注重引导学生不断地积累基础数学知识、技能以及经验等相关知识。

例如，在“分数与小数的四则混合运算”部分数学问题求解期间，为了简化学生的计算过程，教师必须要引导学生可以灵活地对小数和分数之间的等价转换进行处理，并要熟练地运用四则运算的相关运算定律，掌握常见基本数学计算模型的计算方法，这些数学基础知识的积累是提升学生解决数学问题的重要基础，也是使学生可以在求解相关数学问题时快速捕捉与找寻解题突破口的关键条件，进而才能使小学生在求解数学问题过程中快速地、准确地做出直观判断。由此可知，小学生如果可以夯实自身的数学基础知识，熟练地运用基本数学技能，并且具有丰富的数学活动经验，那么都非常容易促进学生直觉思维的发展。

2.数形结合，引导学生感受数学直觉思维

对小学数学知识的构成而言，其主要可以分成“数”与“形”两部分，或者说“数”与“形”是构成数学知识的两种重要形式，也是小学生正确认识和研究数学问题中的两种知识形式。“数”与“形”二者之间具有紧密联系，其中“数”的量化性更强，“形”的直观性更强，二者相互融合才能更好地理解数学知识。而为了引导学生切实体会与感受小学数学直觉思维，教师可以灵活地运用图形的形式对数学原理进行直观展现，这样也更容易启发学生的直觉思维，最终有利于提升学生的空间想象力和数学解题能力。

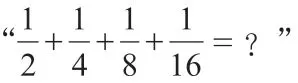
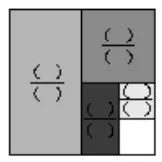
图1

3.猜想论证，促进学生数学直觉思维发展

为了有效地发展小学生的数学直觉思维发展，猜想、论证是非常有效的手段。通过对小学数学问题的情境、结构、数据以及图形等特征进行认真的分析、比较、观察与判断，那么可以在引导学生积极开展有效性、合理性猜测的过程中有效地发展自身的直觉思维。同理，实验论证等方式也是纠正学生直觉猜测缺陷的一个有效手段，对发展他们的直觉思维同样会产生积极影响。

例如，在学习“三角形的内角和”部分数学知识期间，教师可以直接为学生提出：“今天我们主要研究‘三角形的内角和’这一课题，你们对此有什么疑问？”引导学生积极开展沟通与交流。在沟通和交流期间，教师要结合小学生的实际学习情况，准确地聚焦“三角形内角和是多少”“三角形内角和是否都保持一致”等问题，引导学生自主猜想和验证。比如，有的学生可能会利用三角尺进行自主验证，这样可以有效提升发展他们的数学直觉思维。

总之，直觉思维是小学生需要具备的一种思维能力。在小学数学中贯彻数学直觉思维培养理念期间，教师可以从厚积薄发，夯实数学直觉思维培养基础入手，通过灵活运用数形结合和猜想论证，力求有效地发展他们的直觉思维，不断提升他们的数学解题能力。