小题大做，自有收获——从一道小题引发的学习思考

湖南省怀化市湖天中学 杨畴遐

解题是增强数学能力的重要途径，思路是否正确、方法是否合理、计算是否简洁是高考得分高低的关键因素。在高考时刻，考生应该小题小做以提高速度，但在平时的学习中，也要注意小题大做来探索规律，积累经验，达到知一题而会一类。我喜欢理科，热爱数学，经常订阅一些数学杂志，从中引发数学思考。

一、问题展示

在学习时，《直线与圆》一节中发现有这类填空题：

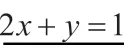
常规思路：1.设过P点的切线方程求出两条切线；2.由切线方程和圆方程求出切点坐标；3.用两点式求出过两切点的连线方程。

二、问题反思

常规解法思路清晰，方法正确，然而过程复杂，计算量很大，费时费力，这绝不是我们所期望的。在课后学习中，我认真思考，细心观察，此类问题是否有简洁解法。

在与同学讨论中发现其结论类似于过圆上一点作圆的切线方程：x·x+y·y=r² ，

在请教老师后，得到了如下解法：设两切点为A（x1，y1）、B（x2，y2），则过A、B的两条切线分别为：x1x+y1y=1 和x2x+y2y=1，又点P（2，1）在两切线上，所以有：2x1+y1= 1，2x2+y2=1。

这说明点A（x1，y1）、B（x2，y2）都在直线2x+y=1 上，而过两点的直线有且只有一条，所以上题所求直线方程必为2x+y=1 。

上列解法“设而不求”，典雅别致，确有事半功倍之效，也正是我们所奢求的解法。

三、问题变更

上列解法是否具有特殊到一般的规律呢？

将上面的点P（2，1）改为P（x'，y'），如图1。圆方程改为更一般的圆的方程：（x-a）2+（y-b）2=r2，点P还是在圆外，于是可得：过切点A、B的直线方程为：（x'-a）（x-a）+（y'-b）（y-b）=r2。

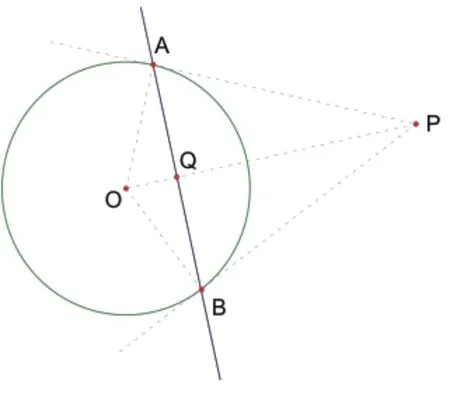
图1

所以我们就有了一般结论：

结论：过圆外一点P（x'，y'）引圆（x-a）2+（y-b）2=r2的两条切线 ，则过两切点的连线方程为： （x'-a）（x-a）+（y'-b）（y-b）=r2（切点弦方程）。

这个结论和过圆上一点P所作出的圆的切线方程是多么相似啊！这个奇妙结论不仅体现了“设而不求”解法的精妙，也让我感受到了数学世界特殊的简洁之美。

四、学习反思

我们知道，点与圆有三种位置关系：圆上、圆外、圆内。现在又知道了这样的结论：

对于点P（x'，y'）和圆（x-a）2+（y-b）2=r2，有：

①P在圆上→（x'-a）（x-a）+（y'-b）（y-b）=r2是过P点的圆的切线方程（与圆相切）；

②P在圆外→（x'-a）（x-a）+（y'-b）（y-b）=r2是由P点获得的切点弦方程（与圆相交）；那么自然产生如下的问题：

③P在圆内→（x'-a）（x-a）+（y'-b）（y-b）=r2有着怎样的几何意义呢？ 与圆有何关系？

由②的图像引起思考（如图2），利用射影定理易得OQ·OP=OA²=r²，所以结合①即得：点P和点Q是对应点，故由点P所得的直线是过Q点且与直线OP垂直的直线。

再由②又看到圆外每一个点在对应圆内一个点的同时也对应着一条弦；反之，可看作圆中每一弦都对应一个点，那么，过P点的弦有无数条，这些对应点有什么规律呢？

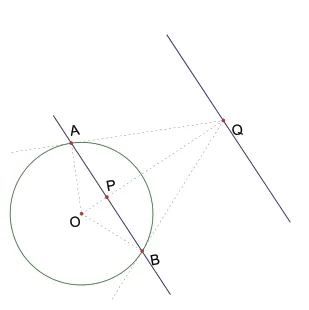
图2

我们再次看看“设而不求”的作用吧：如图3，设过P点的动弦所对应的点为Q（xQ，yQ），则动弦AB的方程为：（xQ-a）（x-a）+（yQ-b）（y-b）=r²，

而点P在动弦AB上，所以有：（xQ-a）（x'-a）+（yQ-b）（y'-b）=r2，这说明所有动点都在直线（x'-a）（x-a）+（y'-b）（y-b）=r2上。

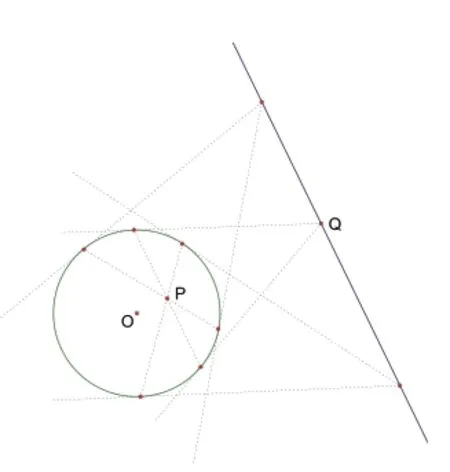
图3

原来该直线竟然就是过P点的动弦的对应点的轨迹，也就是说，是以过P点的动弦端点为切点的两切线交点Q的轨迹方程。

五、思维发散

对于上述③的结论换一个看法，同时又引出了几个新的思考：

1.将点Q看作是圆外的一直线上的动点，则其对应弦都是过点P的弦，同时这些弦的中点亦即点Q的对应点P'的轨迹是以该直线的对应点与圆心为直径的一个小圆。（如图4）

2.若点Q是在与圆相离的圆上的动点，则点Q的对应点P'的轨迹是什么？点Q的对应弦的轨迹有什么规律？（如图5）

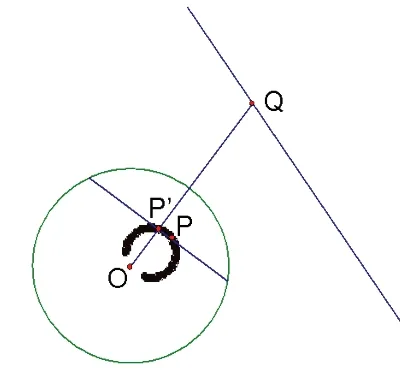
图4

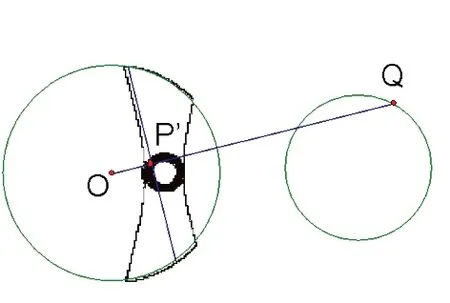
图5

3.若点Q是在与圆内含的圆上的动点，则点Q的对应点P'的轨迹是什么？点Q的对应线的轨迹有什么规律？（如图6）

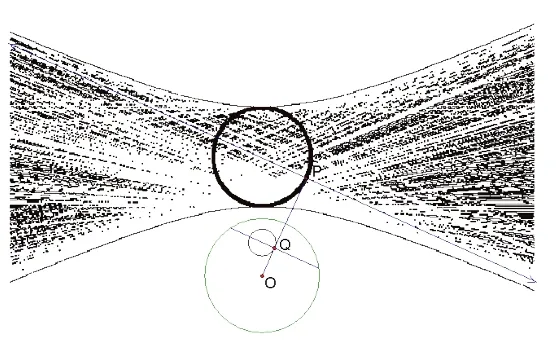
图6

4.若点Q是圆内一弦上的动点，则点Q的对应点P'的轨迹是什么？点Q的对应线的轨迹有什么规律？（如图7）

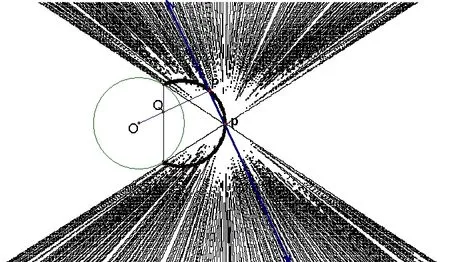
图7