综合法与分析法：数学解题运用解析

江苏省沭阳县沭阳如东实验学校 袁青超

综合法与分析法是数学解题中两个最基本的方法，是思维方向截然相反的两种方法，它们在数学解题过程中有着十分重要的作用。因此，我们在平时的教学中要有意识地渗透给学生, 让他们切实地掌握这两种方法，形成真正的分析问题和解决问题的能力，这也是发展学生思维能力的需要。

综合法是从问题的已知条件出发，经过逐步的逻辑推理，最后达到待证结论或需求问题，即“已知→结论”；分析法是从问题的待证结论或需求问题出发，一步一步地探索下去，最后到题设的已知条件，即“结论→已知”。

例1：如图1，AB∥CD，CE=DE。求证：∠AEC=∠BED。

本题的条件清楚明了，利用平行可证明角相等；利用等边证等角；然后等量代换，就可以得出一对我们求证的角相等。

综合法：因为AB∥CD（已知），

所以 (两直线平行，内错角相等)，

由此可见，我们从已知条件出发，不断地展开思考，去探索结论，这就是综合法，即“由因导果”。

例2：如图2，在△ABC中，AB,AC的垂直平分线l1,l2相交于点O。求证：点O在BC的垂直平分线上。

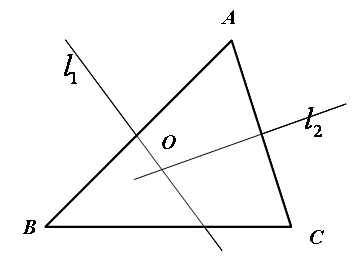
图2

这道题如果从条件出发，说明三角形三边的垂直平分线交于同一点，学生在思考时可能会对已知的两条垂直平分线无从下手；而我们再来看看问题的结论，很明显，要用到线段垂直平分线的判定定理，就是证明点O到线段BC两端的距离相等，于是添上辅助线就可以解决了。

分析法：要证点O在BC的垂直平分线上，

只需要连接OB,OC，去证明OB=OC。

而已知l1是边AB的垂直平分线，可以证明OA=OB，

又已知l2是边AC的垂直平分线，可以证明OA=OC，

所以OB=OC成立。

由此可见，我们从结论出发，不断地去寻找需知，甚至添加辅助线的条件，直至达到已知事实为止，这就是分析法，也就是“执果索因”。

分析法利于思考，综合法益于表达。但事实上，在解题过程中，分析和综合并不是孤立的，而是互相联系的，我们经常把两种方法协同运用，称为综合分析法。对于一些复杂的数学命题，无论是从“已知”到“未知”还是从“未知”到“已知”，都有一个漫长的过程。单靠分析法或合成法更难。为了保证勘探方向的准确和过程的快速，人们经常同时采用分析法和综合法，即综合分析法。从知识和结论出发，我们应该找到问题的中间目标。

例3：如图3，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线交于点C，∠A=30°。求证：AB=2BC。

下面是运用综合分析法思考的过程：

分析：要证明AB=2BC，要么证全等或相似，要么利用三角函数。

图3

综合：条件中的直径和切线都可以构造直角三角形，特别是∠A=30°，那么∠A在直角三角形中所对的直角边等于斜边的一半。

因此，我们要找到以AB和BC为斜边、直角边的直角三角形，很显然图中没有，但有以AB和BD为斜边、直角边的Rt △ABD。

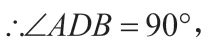
∴AB=2BD。

分析：要证AB=2BC，只要证BC=BD,即证明 。

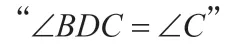
证明：如图4，连接OD。

因为CD是⊙O的切线，

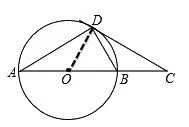
图4

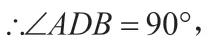
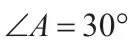
由此可见，从已知到中间目标运用综合法思索，而由结论到中间目标运用分析法思索，以中间目标为桥梁沟通已知与结论，构建出证明的有效路径。

数学家毕达哥拉斯曾这样说过：“在数学的天地里，主要的不是我们知道什么，而是我们怎么知道什么。”因此，在平时的解题教学中，我们要潜移默化地引导学生学会用综合、分析的眼光去看问题，去解决问题；我们要帮助学生树立解题的目标意识，教会他们看清题目的已知条件、已有数据，理清题目的目标与条件之间的逻辑关系，通过综合法和分析法寻找所需的路径和方法，找到它们之间的因果关系以及因果关系之间的关联所在。