强乘积图的Euler性

阴浩然李峰

(1.青海师范大学计算机学院,青海 西宁 810008;2.青海省藏文信息处理与机器翻译重点实验室,青海 西宁 810008;3.藏文信息处理教育部重点实验室,青海 西宁 810008)

1 引言

图G=(V(G),E(G)),其中V(G)是G的非空顶点集,E(G)⊆V(G)×V(G)是G的边集.|V(G)|是图G中的顶点数目,称为图G的阶.对于任意顶点x∈V(G),记图G中所有与x相邻的顶点的集合为NG(x),dG(x)=|NG(x)|表示x在G中的度数.本文所考虑的图都是简单连通无向图,未说明的记号和术语可参见文献[1].

图G的一条途径是指一个顶点和边交替组成的有限非空序列

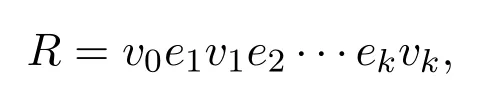
使得边ei的端点为vi−1和vi,i=1,2,···,k.其中顶点v0和vk分别称为途径R的起点和终点,而v1,v2,···,vk−1称为R的内部顶点.如果途径R中的边e1,e2,···,ek互不相同,那么R称为迹.经过图G中每条边的迹称为G的Euler迹.起点和终点不同的Euler迹称为Euler通路.起点和终点相同的Euler迹称为Euler环游,即Euler环游是闭的 Euler迹.如果一个图包含 Euler环游,那么这个图称为 Euler图.因为简单图中的任意两顶点之间至多有一条边,所以途径v0e1v1e2···vkek由它的顶点序列v0v1···vk所确定,因此简单图的途径可用其顶点序列来表示.

强乘积图的概念是文献[2]首先提出的.两个无向图

的强乘积是一个无向图,记为G1?G2.它的顶点集为

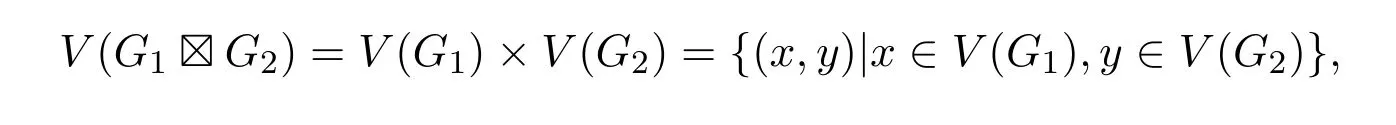
任意两个不同的顶点 (x1,y1)和 (x2,y2)(其中x1,x2∈V(G1),y1,y2∈V(G2))相邻当且仅当x1=x2且 (y1,y2)∈E(G2),或者y1=y2且 (x1,x2)∈E(G1),或者(x1,x2)∈E(G1)且(y1,y2)∈E(G2).图G1和G2称为强乘积图G1G2的因子.由强乘积构造出来的大图包含乘积因子图作为它的子图,并且保留了因子图的许多好性质,比如,连通性、点可迁性、可嵌入性等(见文献[3-5]).更多关于强乘积的知识可见文献[2-7].

瑞士数学家Euler于1736年发表了一篇论文“哥尼斯堡的七座桥”,不仅解决了著名的“七桥问题”,更开创了数学的一个新分支—图论.关于一个图的Euler环游存在性、求解和计数问题引起了许多作者的兴趣.1999年,文献[8]研究了完全图K2m的 Euler环游构造问题,并且给出了一个求解该类图Euler环游的算法.2010年,文献[9]研究了二部图的Euler环游问题,并对该类图的Euler环游数目和性质进行了刻画.更多关于Euler图的知识可见文献[10-11].

本文主要是研究强乘积图中Euler环游和Euler通路的存在性问题.因为强乘积图G1G2是由乘积因子图G1和G2构造出来的,所以因子图G1和G2的拓扑结构必然会影响着强乘积图G1G2的拓扑结构.研究强乘积图的Euler迹问题时,也就是研究乘积因子图的拓扑结构对强乘积图Euler迹存在性的影响.据此,本文给出了强乘积图含有Euler环游和Euler通路的一个充分必要条件。

2 主要定理及证明

定理 2.1设G1和G2是两个非平凡的连通图.强乘积图G1G2是Euler图当且仅当G1和G2中的每个顶点的度数是偶数.

证明设G1和G2中的每个顶点的度数是偶数.由于G1和G2都是非平凡的连通图,根据强乘积的定义,易知强乘积图G1G2也是非平凡的连通图.设T是G1G2的所有迹中最长的一条,并且记为以下形式

可以断言

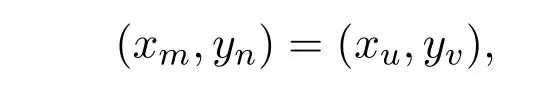
如若不然,迹T终止于(xm,yn)(xu,yv).根据迹的定义,迹T的终点(xm,yn)可能作为T的内部顶点出现过多次,并且每出现一次都会关联强乘积图G1G2的两条边.又因为迹T终止于顶点(xm,yn),所以可以得到顶点(xm,yn)与奇数条边相关联.由于顶点xm∈V(G1)和yn∈V(G2)的度数为偶数,根据强乘积图的定义有

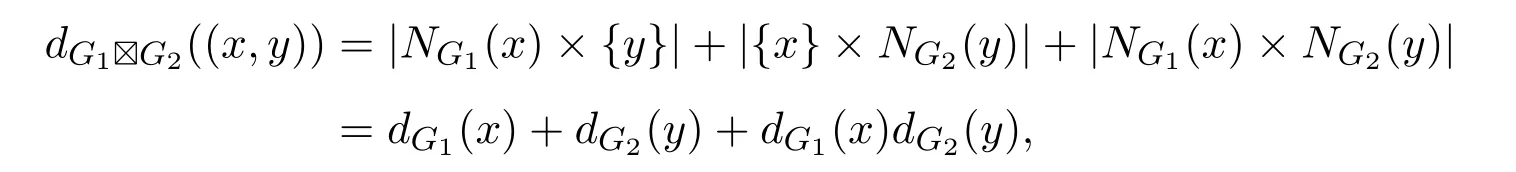
因此顶点(xm,yn)的度数为偶数.更一般地,可以得到强乘积图G1G2中任意顶点的度数是偶数.由此可知顶点(xm,yn)至少还关联一条不在迹T中的边,假设这条边为((xm,yn),(xm+1,yn+1)).此时,可以得到一条比T更长的迹T+(xm+1,yn+1),这矛盾于T是最长迹.因此强乘积图G1G2的最长迹T是一条起点和终点相同的迹,即闭迹.设C=T并且记为

C是G1G2的最长迹且是闭迹.如果C包含强乘积图G1G2的所有边,那么C是G1G2的一个 Euler环游,即强乘积图G1G2是 Euler图.否则,假设C未包含G1G2所有的边.因为G1G2是连通的,所以一定存在着某条不在C中的边e=((xb,yd),(xi,yj))与C上的顶点(xb,yd)相关联.设H=G1G2−E(C),即图H是由强乘积图G1G2删去C中的边而得到的.取H中包含边e的连通分支H1,H1是非平凡且连通的.因为闭迹C中的每个顶点关联G1G2的偶数条边,所以图H中的每个顶点度也关联着偶数条边,对于连通分支H1亦是如此.现考虑H1中起始于顶点(xb,yd)的一条最长迹.利用上述相似方法,可知这条最长迹必须终止于起点 (xb,yd),记这条闭迹为C′.据此,在闭迹C到达顶点(xb,yd)时,把C′粘到C上,可以得到一个比C更长的闭迹,这导致矛盾.因此,C包含了强乘积图G1G2所有的边,从而C是G1G2的一个Euler环游,即强乘积图G1G2是Euler图.

反之,设强乘积图G1G2是Euler图,C′是G1G2的一个Euler环游,记为

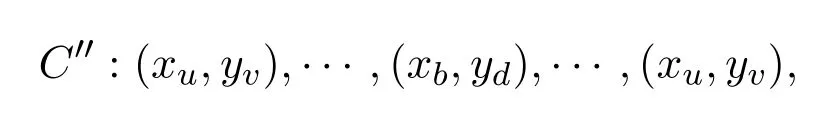
顶点 (xb,yd)是 Euler环游C′的内部顶点 (可能存在 (xb,yd)=(xu,yv)).根据 Euler环游的定义,易知(xb,yd)作为C′的内部顶点每出现一次,就会有强乘积图G1G2中两条边与之关联.因为Euler环游C′包含了G1G2中所有的边,所以对于强乘积图中的顶点 (xb,yd)(xu,yv),有偶数条边与之相关联.又因为Euler环游C′是起始并且终止于顶点(xu,yv)的,所以与顶点(xu,yv)相关联的边的条数也为偶数.综合上面的讨论,对于强乘积图G1G2中的任意顶点(xi,yj),与它相关联的边的条数为偶数,即G1G2中的任意顶点(xi,yj)的度数是偶数.又因为

因而可以得到G1的任意顶点xi的度数为偶数且G2的任意顶点yj的度数也为偶数,即G1和G2中的每个顶点的度数是偶数.

定理 2.2设G1和G2是两个连通图.

(1)如果G1中每个顶点的度数都是偶数且G2恰有两个度数为奇数的顶点,那么在强乘积图G1G2中存在k=|V(G1)|条边不交的迹T1,T2,···,Tk,使得

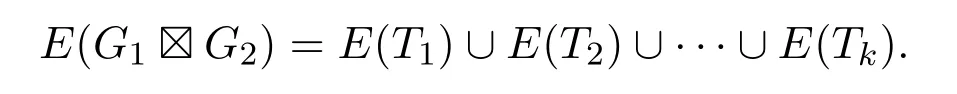
(2)如果G2中每个顶点的度数都是偶数且G1恰有两个度数为奇数的顶点,那么在强乘积图G1G2中存在k=|V(G2)|条边不交的迹T1,T2,···,Tk,使得

证明仅证明(1),(2)可类似证明.设图G1的每个顶点的度数都是偶数且G2恰有两个度数为奇数的顶点.由于图G1和G2都是连通图,根据强乘积定义,易知强乘积图G1G2是连通且非平凡的.令k=|V(G1)|,设G1的顶点为x1,x2,···,xk,G2的两个度数为奇数的顶点为y1和y2.对于强乘积图G1G2的任意顶点(x,y),其中x∈V(G1),y∈V(G2),根据强乘积的定义可知

据此,在强乘积图G1G2中有且仅有如下2k个度数为奇数的顶点:

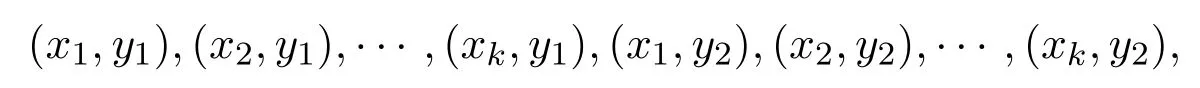
在G1G2中添加连接顶点 (xi,y1)和 (xi,y2)的新边ei(i=1,2,···,k),所得到新的连通图记为 (G1G2)∗,即

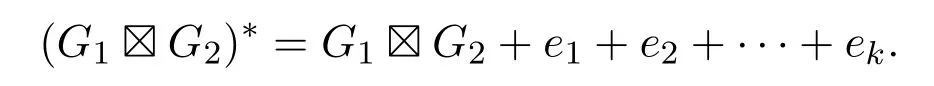
设T是图(G1G2)∗中最长的迹,记为

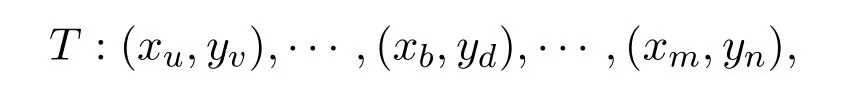
可以断言(xu,yv)=(xm,yn).若不然,迹T终止于(xm,yn)(xu,yv).根据强乘积的定义,顶点(xm,yn)可能作为T的内部顶点已经在终点前出现过,并且每出现一次都有(G1G2)∗中的两条边与之关联.又因为T终止于顶点(xm,yn),所以就有奇数条边与顶点(xm,yn)关联.根据(G1G2)∗的构造方法,可知(G1G2)∗中每个顶点的度数都是偶数.由此可知顶点(xm,yn)至少还关联着一条不在T中的边,设该边为e′,那么可以得到 (G1G2)∗的一条迹T+e′,这矛盾于T是最长迹.因此图 (G1G2)∗的最长迹T是一条闭迹.这里将证明:图(G1G2)∗的最长闭迹T包含其所有的边,即T是 (G1G2)∗的一个 Euler环游.假设不然,T未包含图(G1G2)∗的所有的边.因为 (G1G2)∗是连通的,所以对于T中的某顶点 (xb,yd),一定存在着一条不在T中的边e′与它关联.设H=(G1G2)∗−E(T),取图H中包含边e′的连通分支H1,H1是非平凡且连通的.因为闭迹T中的每个顶点关联(G1G2)∗的偶数条边,所以图H的每个顶点的度数为偶数,也说明了连通分支H1的每个顶点度为偶数.现考虑H1中起始于顶点(xb,yd)的一条最长迹,根据上述讨论,这条最长迹必须终止于顶点 (xb,yd),记这条闭迹为T′.此时,在迹T到达顶点 (xb,yd)时,把T′粘到T上,从而可获得(G1G2)∗中一个比T更长的迹,这导致矛盾.故图(G1G2)∗的最长闭迹T包含其所有的边,即T是(G1G2)∗的一个Euler环游.接下来,从T中删除连接 (xi,y1)和 (xi,y2)的边ei(i=1,2,···,k),即T−e1−e2−···−ek,可以得到强乘积图G1G2中k=|V(G1)|条边不交的迹T1,T2,···,Tk,使得

本定理得证.

定理 2.3设G1和G2是两个连通图.强乘积图G1G2含有一条Euler通路当且仅当G1和G2之一是平凡图,而另一个恰有两个度数为奇数的顶点.

证明设图G1和G2之一是平凡图,而另一个恰有两个度数为奇数的顶点,根据定理2.2,可知强乘积图G1G2含有一条Euler通路.

反之,设强乘积图G1G2的Euler通路为L,记为

顶点(xb,yd)作为L的内部顶点每出现一次,就会有G1G2中的两条边与之关联.因为Euler通路L包含了强乘积图G1G2中所有的边,所以对于所有不同于起点和终点的内部顶点,它们的度数为偶数.又因为L起始于顶点 (xu,yv)且终止于顶点(xm,yn),所以起点(xu,yv)和终点(xm,yn)的度数为奇数.根据强乘积的定义,有

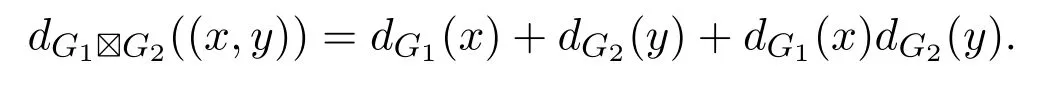
因为(xu,yv)的度数为奇数,所以xu和yv中至少有一个顶点度数为奇数.不妨设顶点xu的度数为奇数,那么顶点(xu,yn)的度数也为奇数.因为强乘积图G1G2仅有起点(xu,yv)和终点(xm,yn)的度数为奇数并且它们是不同的顶点,所以可以得到下面两种情况:(1)yn=yv且xuxm;(2)xu=xm且ynyv.由于无向图中度数为奇数的顶点有偶数个,若xu=xm,则在Euler通路L中必然存在着不同于起点和终点且度数为奇数的顶点,导致矛盾.因此可以得到只有(1)成立,即yn=yv且xuxm.对于L中不同于起点和终点的任意内部顶点(xb,yd),可以断言yd=yn=yv和顶点xb的度数为偶数.如若不然,(xu,yb)和(xm,yb)或者(xb,yd)为L中不同于起点和终点且度数为奇数的内部顶点,导致矛盾.综上可以得到,G2是平凡图且G1恰有两个度数为奇数的顶点.同理,不妨设顶点yn的度数为奇数.利用上述相似方法,可以得到G1是平凡图且G2恰有两个度数为奇数的顶点.

3 结论

强乘积是通过若干特定的阶数较小的图来构造大图的有效方法,也是一种设计大规模互连网络的重要方法.本文研究强乘积图的Euler迹问题,给出了强乘积图是Euler图的充分必要条件和强乘积图含有Euler通路的充分必要条件.