Analytic solutions to the one dimensional time fractional Keller-Segel model

Hou Jie,Wang Lizhen

(School of Mathematics,Northwest University,Xi′an 710127,China)

Abstract：In this paper,the generalized separation variable method,homogenous balanced principle and invariant subspace method are developed to study the generalized Burgers equation with fractional derivatives.With the help of the relation between the parabolic-elliptic Keller-Segel equations and Burgers equation,several exact solutions of the one-dimensional fractional Keller-Segel equations are established.

Keywords：generalized separation variable method,homogenous balanced principle,invariant subspace method,generalized Burgers equation,Keller-Segel model

1 Introduction

Fractional partial differential equations(PDEs)appear more and more frequently in different research fields and engineering applications,such as biology,physics,rheology,control theory,signal processing and electrochemistry[1-2].There are many methods introduced to discuss the construction of solutions to fractional PDEs,such as Lie symmetry method[3-4],generalized differential transform method[5],Adomian decomposition[6],homotopy perturbation[7],which have achieved significant progress for some fractional PDEs.

The generalized separation variable method can split the original equation into several ordinary differential equations(ODEs)[8].The time-fractional heat conduction equation[9],fractional Korteweg-de Vries equation[10],two and three-dimensional timefractional telegraph equations[11]and nonlinear time fractional biological population model[12]were discussed by separation variable method.And the function expansion method of separation variable type based on the homogenous balanced principle was introduced in reference[13].And Rui[14]has studied the exact solutions of nonlinear fractional PDEs.The invariant subspace method is another method for finding the analytical exact solution of the fractional PDEs.This method was initially proposed by reference[15].General fractional ODEs[16],Burgers equation under the Caputo derivative[17]and time fractional coupled nonlinear PDEs[18]were investigated by the invariant subspace method.And the homogenous balanced principle and the invariant subspace method are both special cases of the generalized separation variable method.

In this paper,we consider the following time fractional one-dimensional Keller-Segel(KS)model

where 0<α<1.Equation(1)is the generalization of a class of parabolic-elliptic equations called KS model that characterizes the chemotaxis phenomenon in biology.The KS model was proposed by reference[19],while the parabolic-elliptic model was introduced due to the fact that the diffusion coefficient of the chemical substance is very large[20].Cauchy problems for Keller-Segel type time-space fractional diffusion was studied in reference[21].

The main discussion of this paper is as follows.In section 2,we begin with some basic definitions and remarks of time fractional PDEs with Riemann-Liouville derivative and Caputo derivative.In section 3,we use three methods to solve the generalized Burgers equation.And in Section 4,with the help of the relation between the generalized Burgers equation and KS equations,the solutions of the KS equations are constructed.

2 Preliminary

In this section,we introduce some definitions and properties of the Riemann-Liouville derivative and Caputo derivative which will be used later.

Definition 2.1Letα>0,the Riemann-Liouville fractional integral operator of orderαof the functionf(t)∈L1([a,b],R+)is defined by

is the Euler gamma function.

Definition 2.2The Riemann-Liouville fractional derivative is defined by

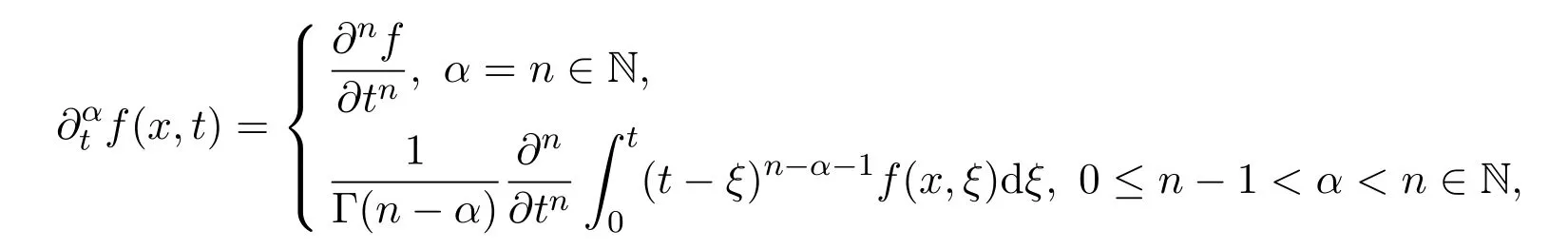
Definition 2.3The Caputo fractional derivative is given by

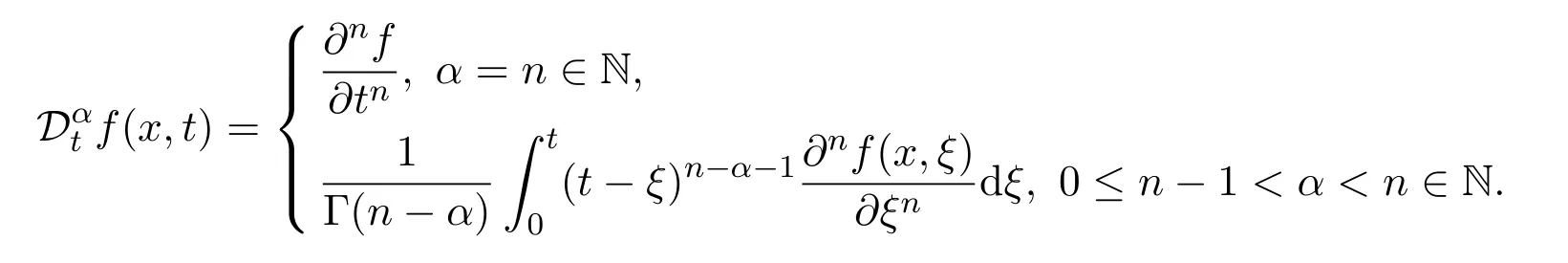
And the following two properties of fractional derivatives and integrals are useful for our discussion.Forγ>0,0<δ<1,t>0,one has

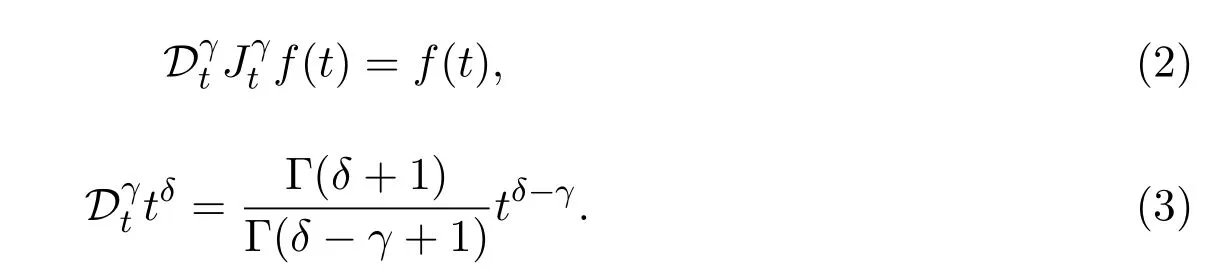
The result related to the solution of the special type fractional ODE is listed as follows.

Lemma 2.1[22]Letα>0,λ,β∈R,λ0.Ifα+β<1,t>a,then theα-th order fractional ODE

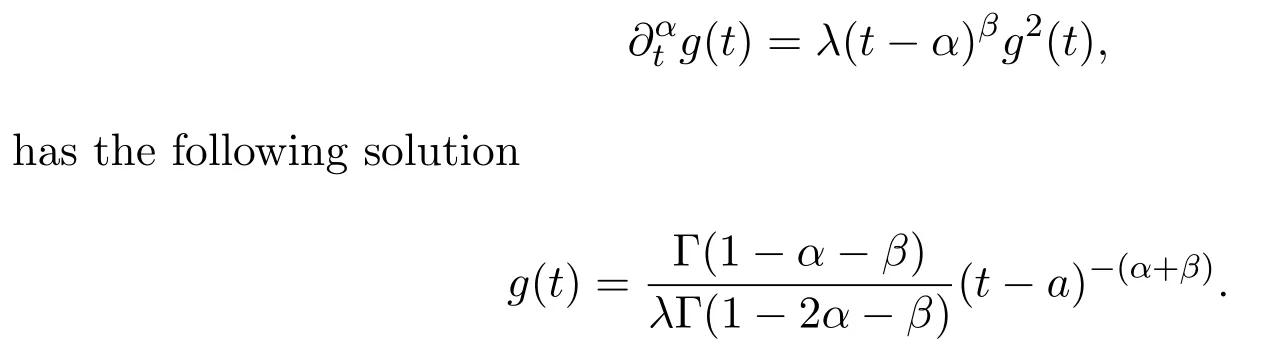
3 The exact solutions of the generalized Burgers equation

In this section,we consider the following generalized Burgers equation

whereh(t)is an arbitrary function oft.We will use the generalized separation variable method,homogenous balanced principle and invariant subspace method to solve equation(4)separately.

3.1 Generalized separation variable method

For generalized Burgers equation(4)with Riemann-Liouville fractional derivative defined by Definition 2.2,we use generalized separation variable method introduced in reference[8]to seek exact solutions of equation(4).

Case 3.1SetSubstituting the ansaze into(4),we can obtain

Using splitting method mentioned in reference[8],we obtain the determining equations

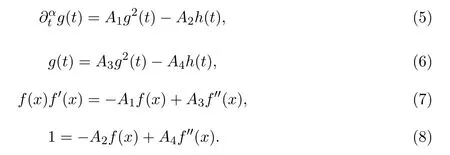
Solving(7)and(8)with the help of Maple yields

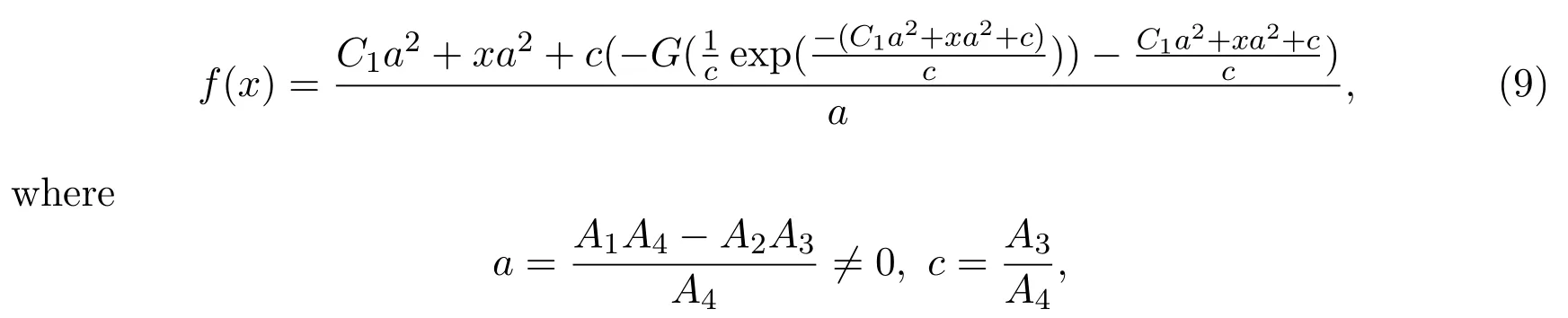
C1is an arbitrary constant,andG=LambertWis the inverse off(w)=wewin whichwis an arbitrary complex number.The combination(5)with(6)gives,

In particular,whenA2=0,solving(10)with the formula given in Lemma 2.1,we find that

Thus,we obtain the following observation on the solution of the Burgers equation.

Theorem 3.1Generalized Burgers equation(4)has solutions of the form

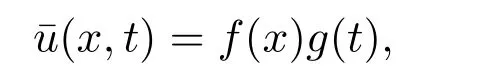
wheref(x)satisfies(9)andg(t)satisfies(10).Especially,whenA2=0,g(t)is given by(11).

Case 3.2Let(x,t)=xg1(t)+f(x)g2(t).Substituting it into(4),we have

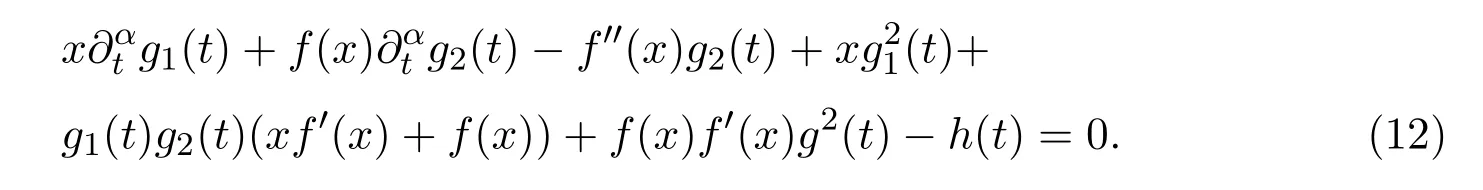
Differentiating(12)with respect toxtwice,and using the splitting method,we obtain the determining equations

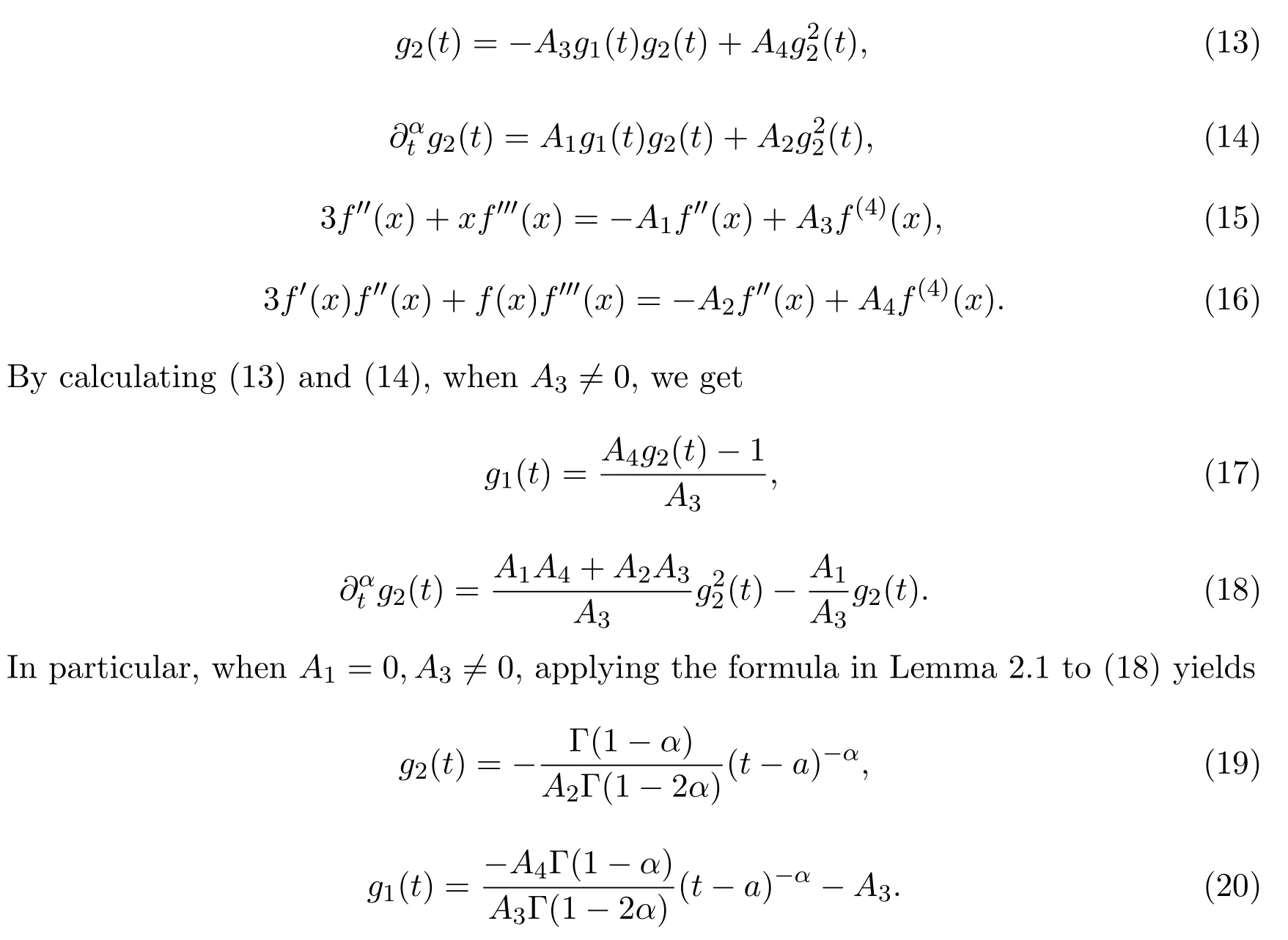
C1,C2,Zare arbitrary constants,andL=RootOfis a placeholder for representing all the roots of an equation in one variable.Thus we have the following result on the solution of(4).

Theorem 3.2Generalized Burgers equation(4)has solutions of the form

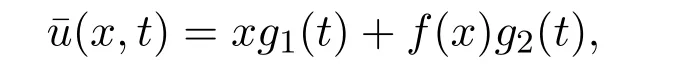
whereg1(t),g2(t),f(x)satisfy(17),(18),(21),separately.Particularly,we obtain the exact solutiong1(t),g2(t)which satisfy(20)and(19),respectively.

3.2 Homogenous balanced principle

In this subsection,we will investigate the exact solution of(4)in Caputo sense,that is,

using homogeneous balanced principle given in reference[14].Suppose

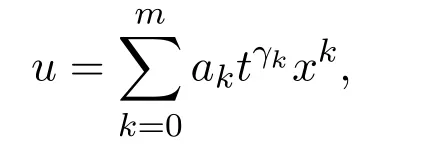
whereak,γkare constants to be determined later.The highest order ofxin the termism.And the highest order ofxin the nonlinearis 2m−1.Thus we obtainm=1 using the homogenous balanced method.Therefore,equation(22)has the following type exact solution

whereγ0,γ1,a0anda1are determined constants.We balance the order oftand the coefficients of every terms in(24)to obtain

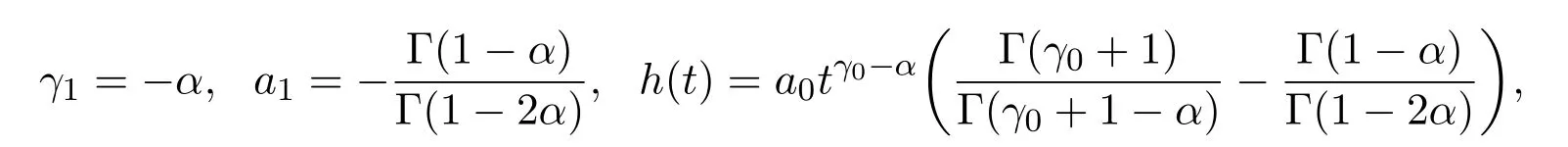
wherea0is an arbitrary nonzero constant,γ0+1>0 andγ0+1−α>0.So,we have the following result.

Theorem 3.3Leta00,γ0>−1+α,the generalized Burgers equation(22)with Caputo fractional derivative has the solution of the form

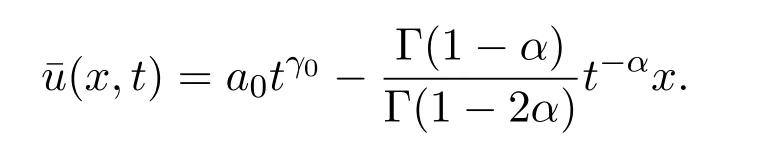
3.3 Invariant subspace method

In this section,we use invariant subspace method to solve the generalized Burgers equation(22).First,we use the invariant subspace method to solve

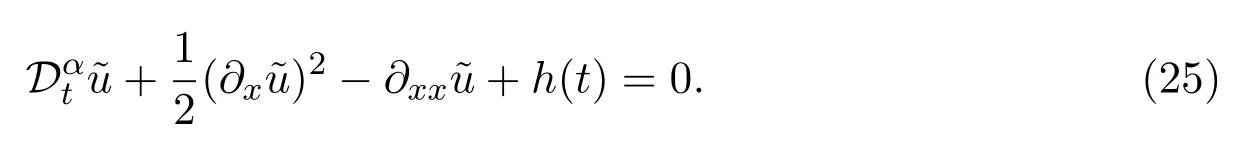
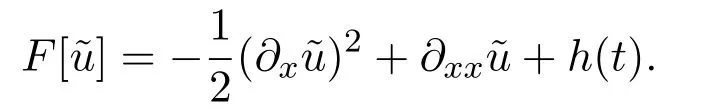
Then we obtain the invariant subspaceW3=<1,x,x2>under the given operatorF[].Thus,the solution has the following form

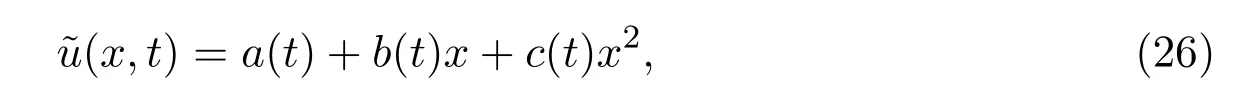
wherea(t),b(t)andc(t)will be determined later.Substitution(26)into(25)yields

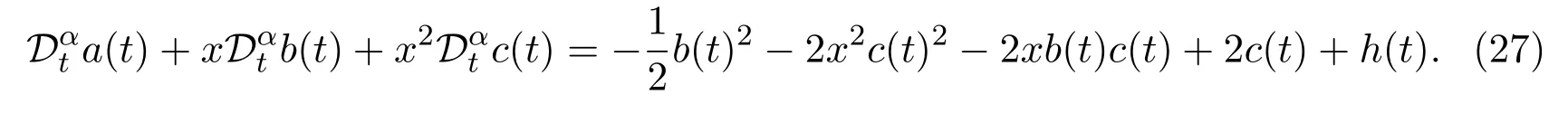
Since equation(27)holds for allx∈R.Therefore,vanishing the constant and the coefficients ofxandx2,we obtain a simple system of fractional ODEs

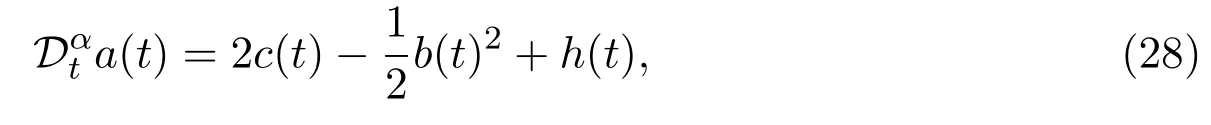
4 The establishment of the solutions of KS equations

Due to the special structure of the parabolic-elliptic KS equations(1),we can transform it into the generalized Burgers equation.In this part,we apply the results of the solutions of generalized Burgers equation to the KS equations to establish the expression of solutions of the KS equations(1).

Integrating(33)with respect tox,we obtain the equation with Riemann-Liouville derivative(4).Using the same method we can find

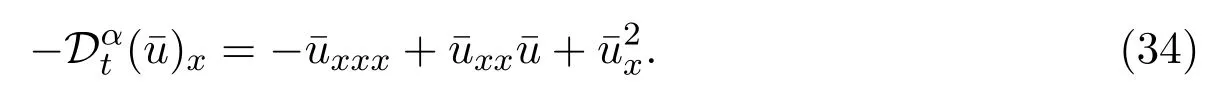
Integrating(34)with respect tox,we obtain the equation with Caputo derivative(22).Therefore,we get the connection between the generalized Burgers equation and the KS equations(1).With the help of these relations,we can deduce the formulas of the solutions to KS equations(1)with the form

Explicitly,applying Theorem 3.1,we get the expression of the solution to the KS equations(1)

wheref(x)satisfies(9)andg(t)satisfies(10).Especially,the exact solutiong(t)satisfies(11).And using Theorem 3.2,the solution of the KS equations(1)takes the form

whereg1(t),g2(t),f(x)satisfy(17),(18)and(21),separately.Particularly,we obtain the exact solutiong1(t),g2(t)satisfy(20),(19),respectively.Exploiting Theorem 3.3,that is,using homogenous balanced principle,we arrive at the solution of the KS equations(1)

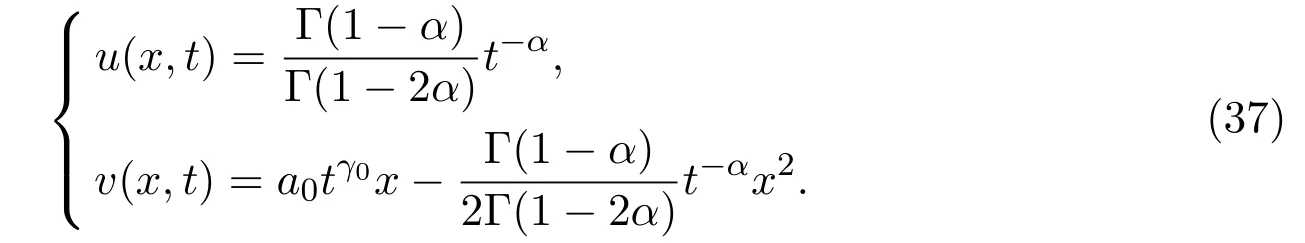
Due to Theorem 3.4,the solution of the KS equations(1)can be expressed

Therefore,we can obtain that equation(35),(36),(37),(38)are the solutions to the fractional one-dimensional parabolic-elliptic Keller-Segel model(1).