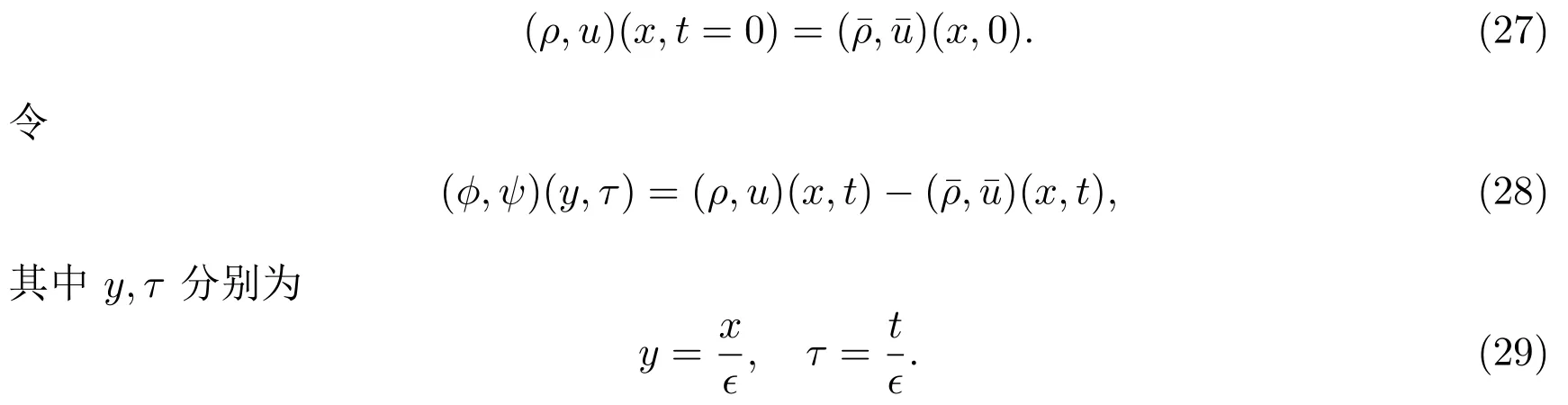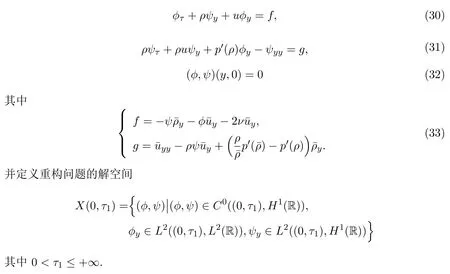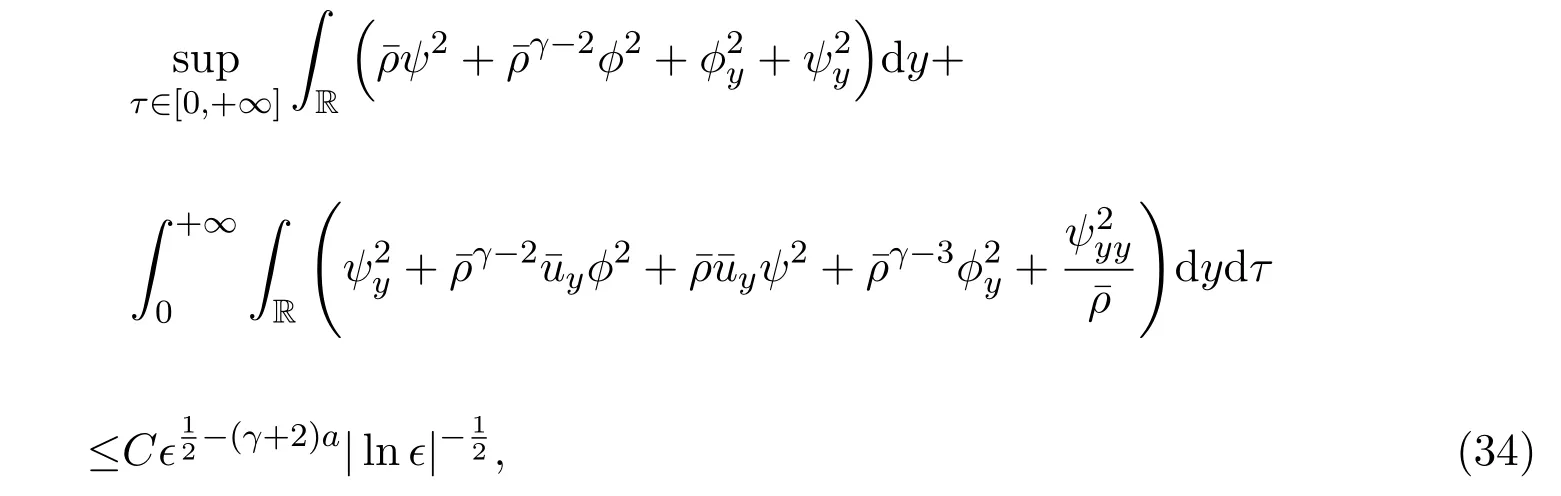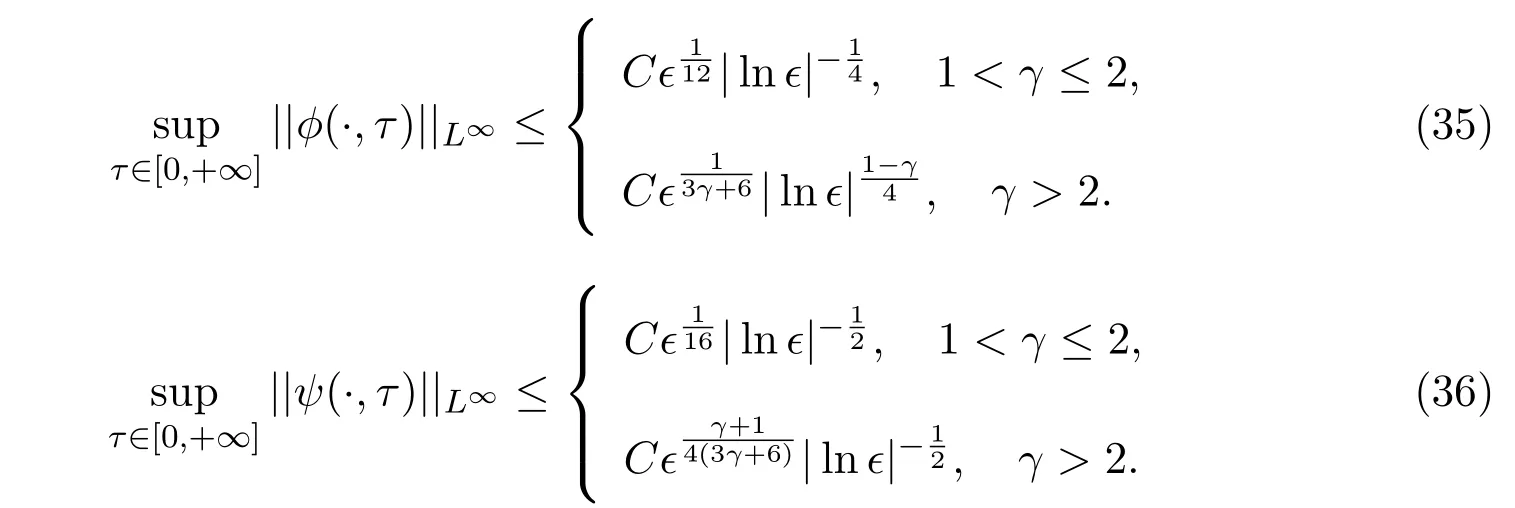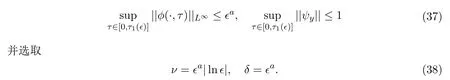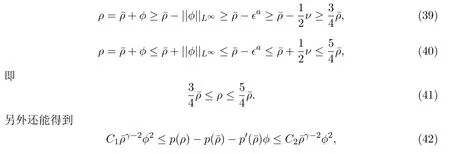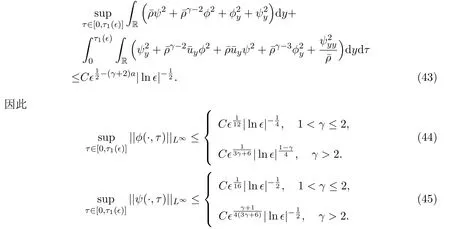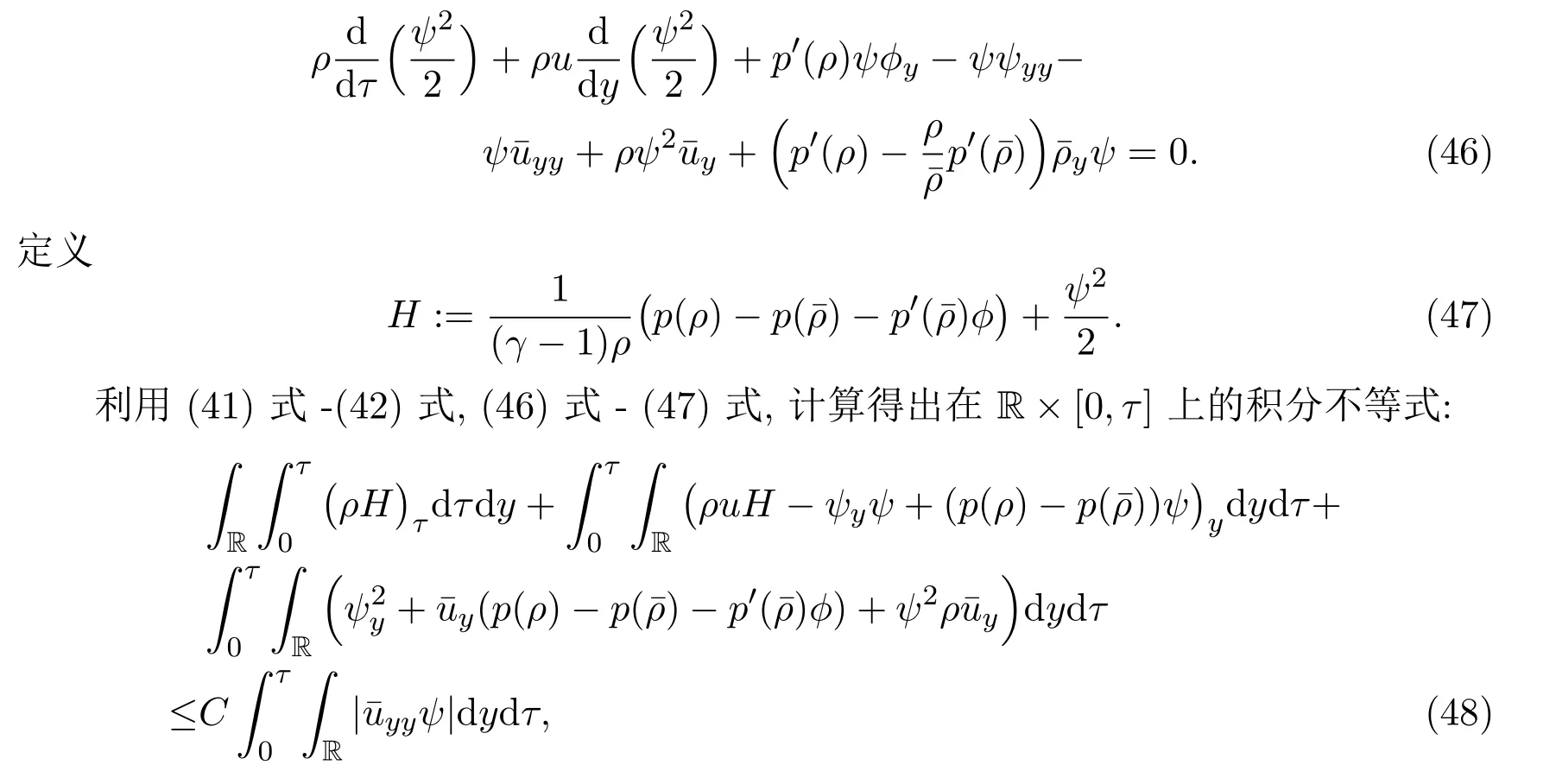一维可压缩等熵Navier-Stokes方程稀疏波在流近似下的零耗散极限
2019-10-24王金妮刘进静
王金妮,刘进静
(西北大学数学学院,陕西 西安 710127)
1 引言
众所周知,一维可压缩等熵Euler方程组为:
其中ρ(x,t)≥0,u(x,t)分别表示流体的密度和速度,表示压力,γ>1为绝热指数.当赋予方程组(1)如下的初值:

其中 (ρ±,u±)均是常数,则 Riemann问题 (1)-问题 (2)的解包含激波、稀疏波和真空[1-2],在这两种非线性波中,仅稀疏波能够与真空连接.
本文考虑当Euler方程组(1)稀疏波解的一端与真空连接时,如下一维可压缩等熵Navier-Stokes方程组的零耗散极限:
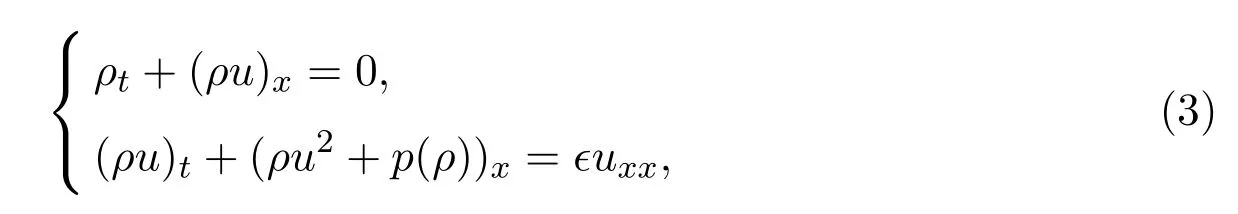
其中ϵ>0为常黏性系数.
随着黏性的消失,黏性流的解强收敛到对应无黏流的解,这类问题即为零耗散极限问题,它是可压缩黏性流体中一类十分重要且具有开放性的问题.当无黏流不包含奇性时,可由经典标量方法得到零耗散极限,而当无黏流包含奇性如激波和真空时,零耗散极限问题富有挑战性.对于可压缩等熵Navier-Stokes方程组,文献[3]首先考虑了包含初始层且Euler方程组的解是单个激波的情形,证明了随着黏性的消失,方程的解趋于黏性激波,基于上述结果,文献[4]证明了在没有初始层的情况下,当Euler方程组包含稀疏波解且不包含真空时,可压缩等熵Navier-Stokes方程组稀疏波解的零耗散极限,且得到一致收敛率.若Euler方程组(1)的初值只在无穷远处无真空,文献[5]利用补偿紧致性的方法得到了方程组(3)的黏性消失极限.关于两个激波复合的情形可以参考文献[6-7].对于非等熵Navier-Stokes方程组的零耗散极限也有了丰富的研究成果[8-13],特别地,文献[10]考虑了可压热传导Navier-Stokes方程组激波解的零耗散极限问题;文献[13]对于稀疏波与接触间断波叠加的情形进行了研究.此外,对于如下黏性双曲守恒律也已经有了一些有意义的成果:
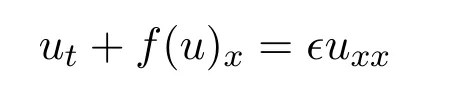
文献[14]利用匹配渐近展开方法研究了激波的黏性消失极限,后来此结果被文献[15]推广到包含初始层的情形.文献[16]在BV空间中研究了解的黏性消失极限问题,随后,文献[17-18]对这一结果进行了改进和推广.
近年来,文献[19]研究了当Euler方程组(1)的解为2-稀疏波+真空时,Navier-Stokes方程组(3)的零耗散极限,并对方程组(1)赋予Riemann初值:
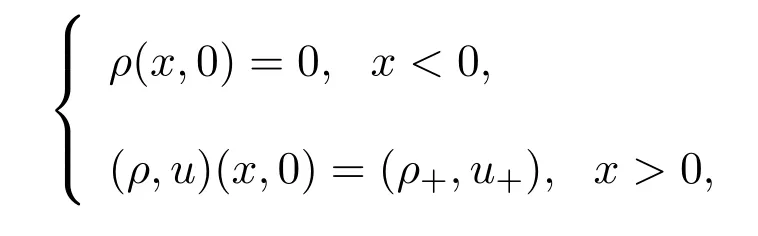
且得到连接真空状态 (0,u1)到 (ρ+,u+)的 2-稀疏波 (ρr2,mr2=ρr2ur2):

其中mr2表示动量,分别表示方程组(1)的特征值和2-Riemann不变量.然后 Huang等人对与真空连接的2-稀疏波 (ρr2,mr2)进行截断处理,并且构造了 Navier-Stokes方程组 (3)的一列解,当黏性ϵ→0时此列解收敛于与真空连接的2-稀疏波(ρr2,mr2),并得到一致收敛率估计.另外,关于黏性依赖于密度的Navier-Stokes方程解的零耗散极限也已经有许多学者研究,具体可参见文献[20-21].
事实上,探究当稀疏波与真空连接时Navier-Stokes方程组(3)的解的零耗散极限关键之一在于如何控制稀疏波中由真空引起的退化,本文将利用流近似方法[22-23]控制退化.从物理学的观点来看,流体是分子结构不抵抗外部剪切力的物质,即使是最小的力也会引起流体粒子的变形;从数学上讲,很小的力可以看作是力学上的流扰动,进而发现合理的扰动可以用来控制流体的某些动力学行为,因此,流近似可以用来控制真空附近的退化.
首先,本文对Euler方程组(1)进行流扰动,即得到扰动Euler方程组:
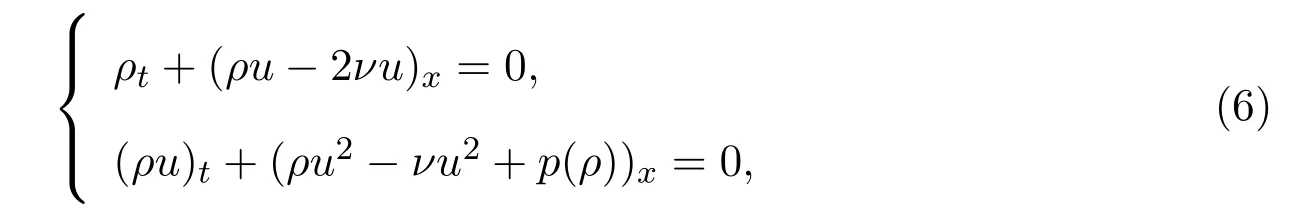
其中密度ρ≥2ν,ν>0为依赖于黏性ϵ的参数.本文将选取ν=ϵa|lnϵ|,其中a由下文(15)式给出.当ν→0时,上述方程组形式上变为Euler方程组(1).事实上,方程组(6)是严格双曲型的,它有两个互异的特征值:
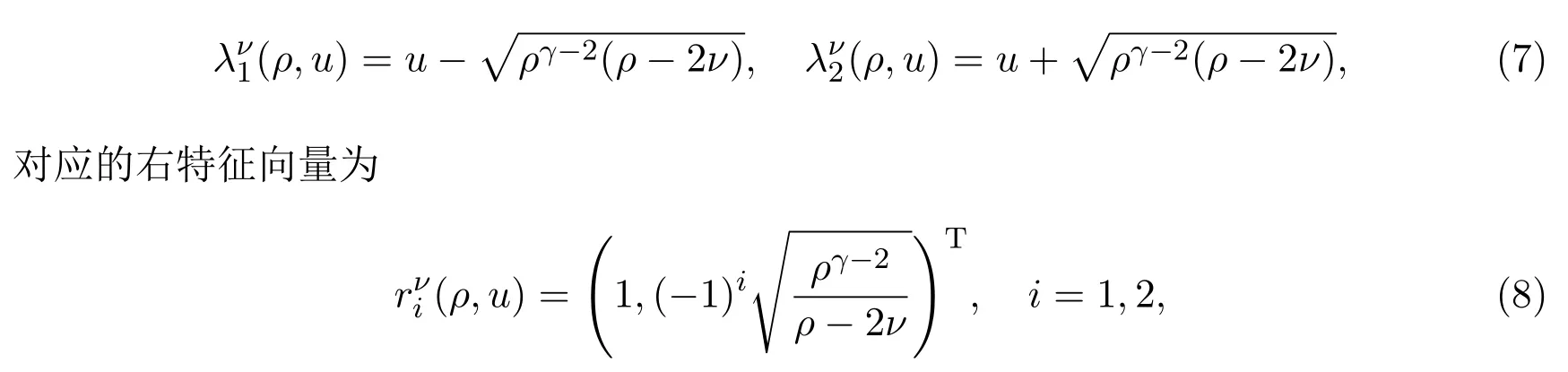
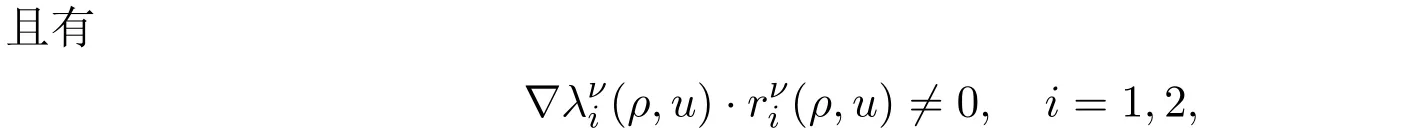
即这两个特征场都是真正非线性的.此外,i-Riemann不变量定义为
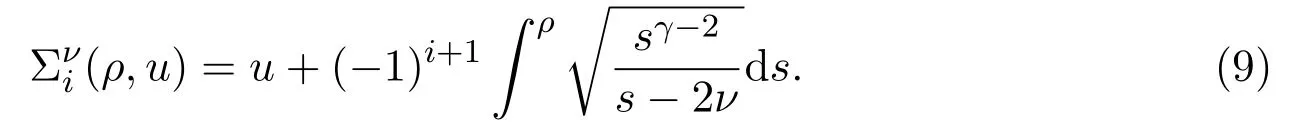
解 Riemann问题 (6),问题 (2),可以得到两类基本波解,即激波 (S1,S2)和稀疏波 (R1,R2),(更多相关细节参见文献 [22]).因此能够得到 5种结构的解 (见图 1),特别地,当 (u+,ρ+)∈V(u−,ρ−)时,Riemann解包含 2个稀疏波和 1个常密度状态 (ρ=2ν).通过对比发现,Riemann问题 (1),问题 (2)的解包含真空状态,而Riemann问题(6),问题(2)的解已不包含真空状态.换言之,已经控制了稀疏波中真空引起的退化.
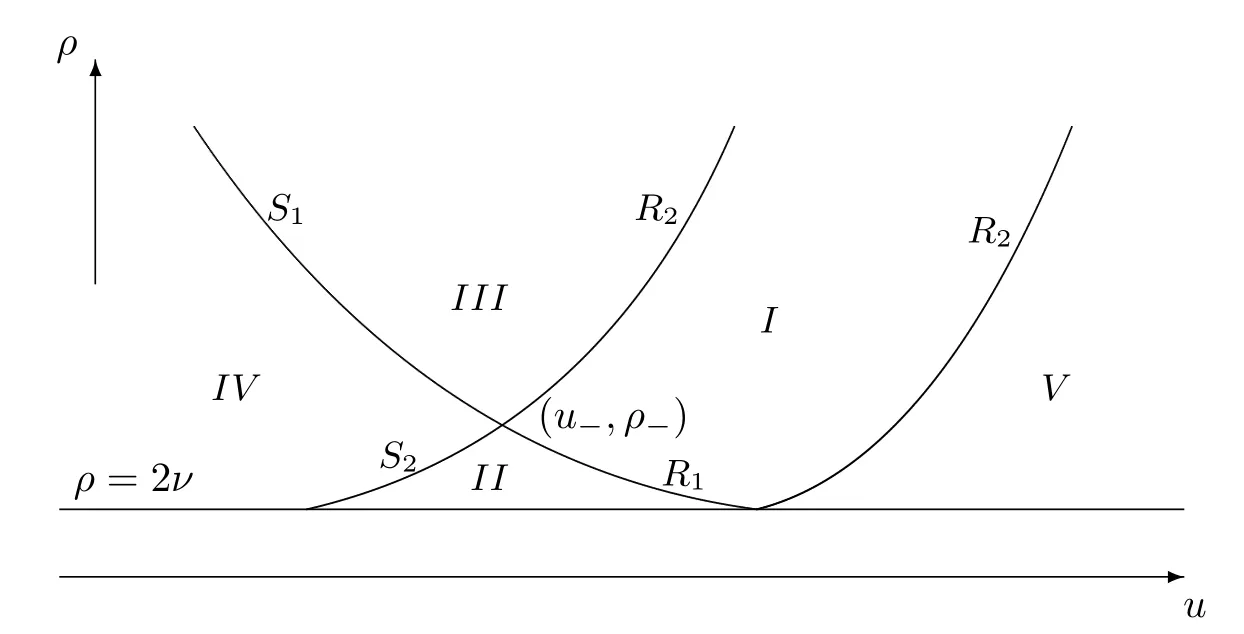
图1 方程组(6)Riemann解的结构
本文仅考虑2-稀疏波.如果给方程组(6)赋予Riemann初值:
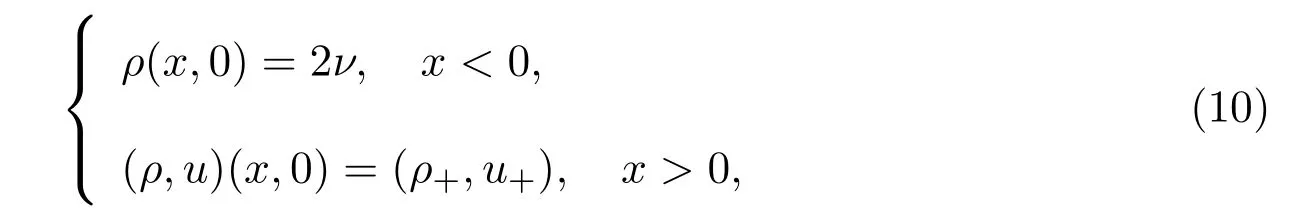
即左状态为常密度,那么连接 (2ν,u∗)到 (ρ+,u+)的 2-稀疏波解
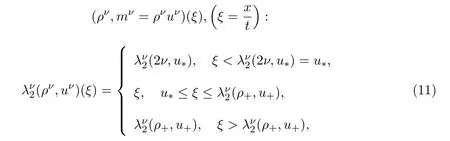
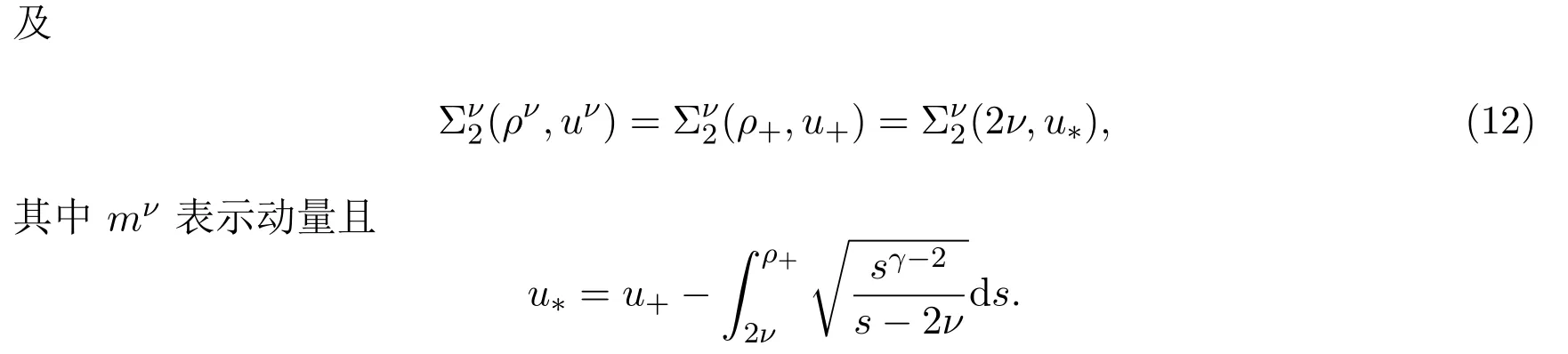
由显示解公式可知当ν→0时,2-稀疏波 (ρν,mν)收敛于由 (4)式和 (5)式定义的 (ρr2,mr2).因此有下面的引理:
引理 1.1存在一个常数ν0∈(0,1),使得对ν∈(0,ν0],t>0有:
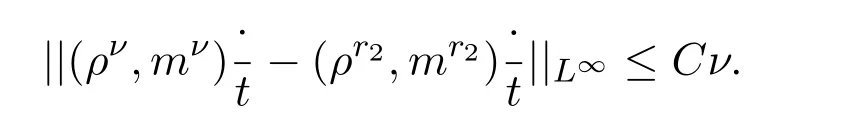
然后,本文利用 Burgers方程对2-稀疏波 (ρν,mν)进行光滑逼近,构造其近似稀疏波.
下面叙述本文的主要结论:
定理 1.1设由(4)式和(5)式定义的是Euler方程组(1)的一端与真空连接的2-稀疏波解,且给方程组(3)赋予初值(27),则存在适当小的正常数ϵ0>0,对任意的ϵ∈(0,ϵ0),可以构造方程组(3)的一列光滑全局解满足:

且当ϵ→0时,(ρϵ,mϵ)(x,t)逐点收敛到 (ρr2,mr2)(x,t)(除点 (0,0)外).
进一步,对于任意给定的常数h>0,存在一常数Ch>0(不依赖于ϵ),成立:
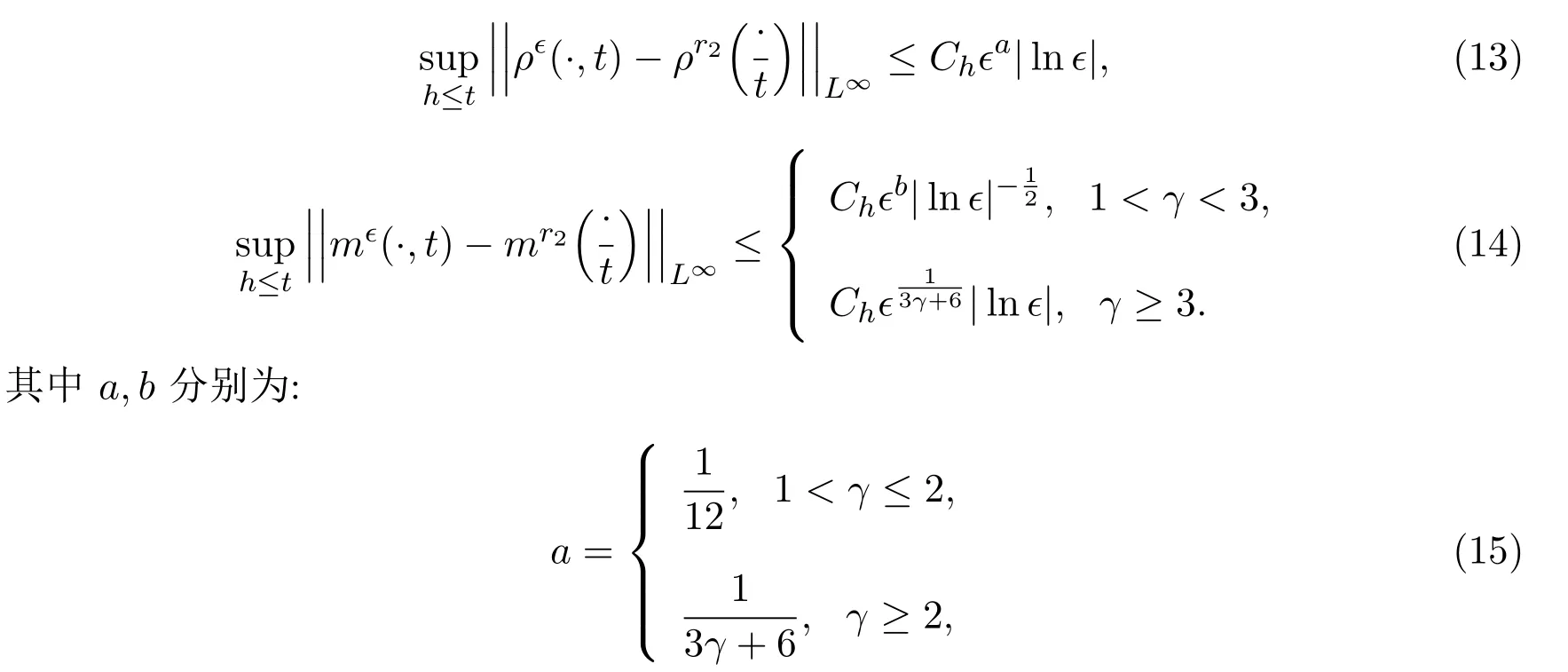

注1.1(i)本文介绍了另一种方法,即运用流近似方法研究一维可压缩等熵Navier-Stokes方程组的零耗散极限.通过以上的分析,可以发现定理1.1中关于ϵ的收敛率与文献[19]中得到的收敛率不同.
(ii)L2(R)表示定义在R上的平方可积实值函数空间,且范数记为||·||:=||·||L2.
(iii)Hk(R)表示常用的 Sobolev空间,且范数记为||·||k,特别地,||·||0=||·||.
近年来,锂离子电池的应用已经逐渐扩展到汽车、家电、电动自行车、储能等领域。2014年,中国锂离子电池产量达52.87亿只,占全球总产量比重达到71.2%, 2018年预计全国锂电池产量达到121亿只,增速22.86%。国内锂离子电池产业进入快速成长阶段,成为全球主要的锂离子电池生产国和消费国。
(iv)C表示不依赖于ϵ和时间t的正常数.
本文剩余内容结构安排如下:第二部分利用无黏 Burgers方程对 2-稀疏波 (ρν,mν)进行光滑逼近;第三部分给出定理1.1的证明.
2 近似稀疏波
受到文献 [4,19,24]中部分思想的启发,本节将利用 Burgers方程建立关于扰动Euler方程(6)稀疏波解的一些必要估计,特别要构造一个光滑稀疏波,使其能够很好地逼近 2-稀疏波 (ρν,mν).
考虑无黏Burgers方程的Riemann问题:
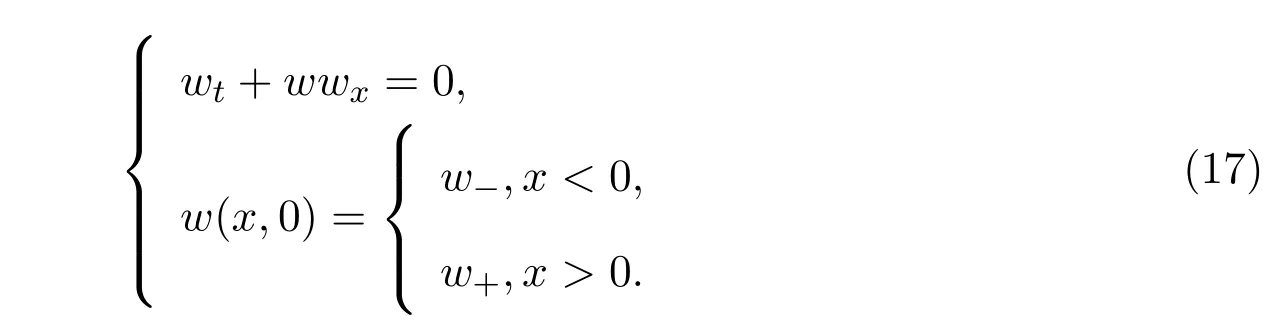
当w− 参照文献[4,19,24],2-稀疏波(ρν,mν)可由下面的Burgers方程进行光滑逼近: 其中δ>0是待定小常数.注意到,方程组(19)存在唯一的光滑全局解 引理2.1的证明参见文献[4,19],这里不再证明. 本节将证明这篇文章的主要结论.记 Navier-Stokes方程组 (3)的解为 (ρϵ,uϵ),为简便起见,省去(ρϵ,uϵ)的上标,即用 (ρ,u)表示方程组 (3)的解.赋予方程组 (3)如下的光滑初始值 把(28)式-(29)式代入方程组(3),并结合方程组(26)得到 引理 3.1重构问题(30)-问题(32)存在唯一全局解(ϕ,ψ)∈X(0,τ1),并且存在某个充分小的ϵ0>0,使得当0<ϵ≤ϵ0时成立: 其中a由方程组(15)给出,因此 随后的分析中,作出先验假设 其中a由方程组 (15)给出,[0,τ1(ϵ)]表示解存在的时间区间且τ1(ϵ)依赖于ϵ.容易发现若ϵ≪1,则ν≥2ϵa成立.根据先验假设(37),得到 其中C1,C2是不依赖于ϵ的正常数. 分析发现一旦得到引理3.1,可立即得到定理1.1.另外,方程(30)-方程(32)解的局部存在定理是标准的,本文不再陈述.[0,∞]上的解可由解的局部存在性和一些先验估计得到,因此这篇文章的主要任务就是得到如下的先验估计: 引理 3.2(先验估计) 设 (ϕ,ψ)∈X(0,τ1(ϵ))是重构问题 (30)-问题 (32)的解,其中τ1(ϵ)表示解存在的最大时间且满足先验假设(37),则存在充分小的常数ϵ0>0,使得当0<ϵ≤ϵ0时成立 接下来证明引理3.2,证明主要分三步进行. 证明(I)给方程(31)乘ψ得到 即完成了引理3.2的证明. 据此可以断言τ1(ϵ)=∞.事实上,如果τ1(ϵ)<∞,则可再次利用解在时间τ=τ1(ϵ) 的局部存在性,找到另一时间τ1(ϵ)<τ2(ϵ) 使得解在 [0,τ2(ϵ)]内满足 (37)式,这与引理3.2中τ1(ϵ)是最大时间矛盾.因此,当ϵ较小但固定时,可以把局部解延拓至全局解.最后,证明定理1.1. 定理 1.1的证明根据引理1.1,引理2.2,引理3.1及ν=ϵa|lnϵ|,δ=ϵa,则对任意给定的常数h>0,存在不依赖于ϵ的常数Ch>0,使得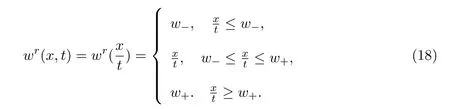

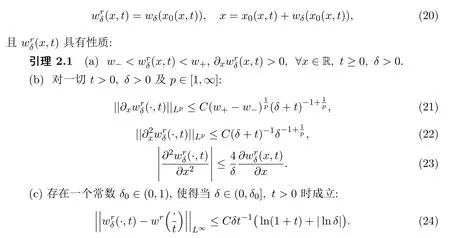

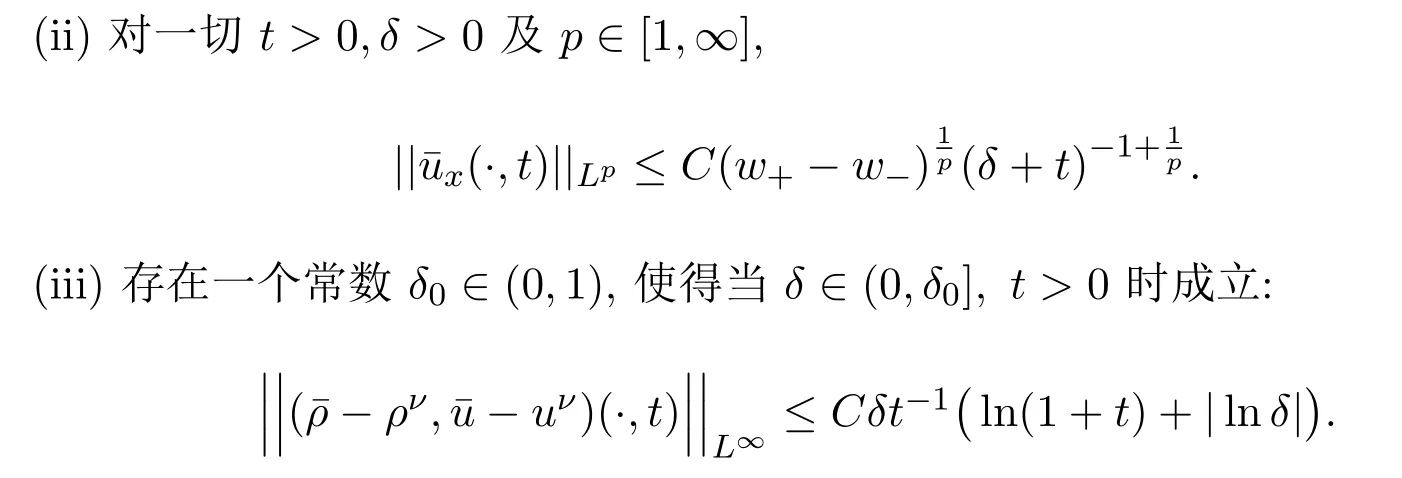
3 定理1.1的证明