数形结合在初中函数教学中的应用

徐大香

【内容摘要】在数学学习实践中，函数知识作为一个重要的知识体系，贯穿初中数学学习的始终。函数知识的学习需要学生借助对平面直角坐标系的有效理解和认识，通过将抽象性的函数知识与形象性坐标系有效地融合，让学生在数形有效结合的基础上，形成对函数知识的生动具体的认识体验，从而达到对函数知识的有效认识理解过程。将抽象的函数知识与形象的直角坐标系有机地结合起来，让学生在形象生动的认识图形与数的关系的有效分析过程中，形成对函数知识的有效理解体验过程。

【关键词】初中数学 函数 数形结合 应用

著名数学家华罗庚指出：“数形结合百般好，数形分离万事难”，数学课程标准也指出：“通过利用图形来描述和分析问题，借助图形直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路”。因此，在初中数学教学实践中，通过数形结合思想的有效渗透，让学生在具体的数学学习实践中，能够有效地分析数形之间的具体关系，从而使学生形成对数量关系间的具体而生动的认识体验，促进学生对问题的有效分析、推理、归纳和总结等，在有效的数形结合体验中，实现对函数知识的生动认识体验。因此，在初中数学教学实践中，如何通过有效策略的实施，使学生在函数学习实践中，通过数形结合，有效建构数学模型，形成对函数知识的生动形象的认识过程，在具体的教学实践中可采取：

一、确立直角坐标系思想，构建代数与几何联系的桥梁

十七世纪法国著名数学家笛卡尔在一次偶然中发现，屋頂上的蜘蛛能够沿着蜘蛛网左右上下爬行，他灵机一动，想到是否可以把蜘蛛看作一个点，它可以上、下、左、右运动，怎样用一组数将蜘蛛的位置确定下来呢？由此衍生了直角坐标系理论。直角坐标系是代数与几何之间的一座桥梁，将抽象复杂的数量关系知识以形象、生动的图示形式展示出来，通过对直观化的图像分析，有效地降低了学生对抽象的数量关系分析的难度，提高了学生的学习效率。

例如在学习《一次函数的应用》的实践中，结合例题“某物体沿一个斜坡下滑，它的速度v（m/s）与其下滑时间t（s）的关系如图所示。

（1）   写出v与t之间的关系式;

（2）   下滑3s时物体的速度是多少？

教师在教学实施的过程中，教师将函数中的数量间的关系，以直观的、形象的、直角坐标系的形式呈现在学生们的眼前，学生通过对图像的观察（因为图像经过原点且呈一条直线，所以这是一个正比例函数的图像）和题意分析可知v与t是正比例函数，由此可设其表达式为v=kt，在有效地结合已知量和变量之间的关系的基础上，形成对一次函数的图像以及数量关系间的有效认识体验，通过有效分析，形成对问题的具体认识。因此，确定直角坐标系思想模型，让学生在对函数问题的形象化的分析实践中，达到问题的有效分析，合理判断，并最终作出对函数问题的有效解答。

二、通过代数化几何，化抽象为直观

在初中数学函数学习实践中，当数与数之间的关系，以文字式的形式展现在学生们的眼前时，以形象思维占优势的初中生对函数的学习兴趣难以有效地调动起来，而在具体的学习实践中，通过将函数代数问题，转换为几何图像，引导学生在图像分析的过程中，形成对函数问题的有效认识体验。

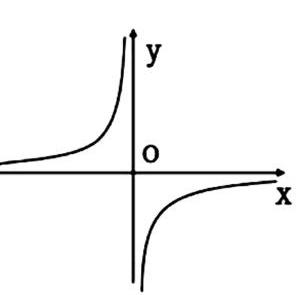
例如在学习《反比例函数的应用》的实践中，分析例题若点（-2，y1）、（-1，y2），（2，y3）在反比例函数y=-2/x的图像上，求y1，y2，y3之间的大小关系。首先根据函数的关系式可以画出其相应的直角坐标函数图像，根据图像所在的象限可以判断出三点所在的象限，进而利用函数图像的增减性来判断三个数的大小关系。以数化形，让数量关系在直观的图像展示的过程中，更加简便、并易于学生理解和认识，因而能够极大地提高学生的学习效率。

三、确立数形互变思想，建构函数思维模型

学生在函数学习实践中，能够熟练地掌握函数的关系式与其图像走势之间的关系，并能够根据具体的数量关系、列出正确的函数关系式，再结合函数关系式来进一步画出函数图像;反之也可通过函数图像，分析出函数的增减性、判断函数的各数量间的关系，进而列出相应的关系式，关系式是判断函数关系的重要标志。确立了数形互变的思想，让学生在具体的学习实践中能够正确、合理、有效地运用，从而使函数思维模型在学生的认知结构中得到有效地构建。

例如在学习《二次函数》的实践中，根据二次函数的关系式，y=ax2+bx+c（a≠0），结合数据分析，能够有效地形成对二次函数图像的开口大小、方向以及对称轴等内容的分析和概括，如二次项系数a决定着二次函数的开口方向和大小，当a>0时，二次函数抛物线图像的开口向上;反之则抛物线图像的开口向下;|a|越大，则二次函数的抛物线开口越小。二次项系数a和一次项系数b决定了对称轴的位置，当两者符号相同时，在对称轴y轴的左侧，反之则在右侧。抛物线与x轴的交点个数则由Δ决定，当Δ=0抛物线与x轴只有一个交点;当Δ>0时，有两个交点;Δ<0时，与x轴没有交点。在对函数的相关数据的分析与理解的实践中，实现数形的有机结合，从而达到对二次函数问题的有效理解和运用，实现课堂学习效果的有效提高。

总之，在函数教学实践中，将数形结合思想在具体的教学实践中的有效渗透，能够极大地降低学习的难度，促进学生的理解、消化和吸收，因而更加有利于学习效果的突出显现。因此，教师应将数形结合思想有效地渗透到数学教学的具体实践中去，以使课堂效果得到良好的体现。

【参考文献】

[1]初中数学教学中数形结合思想的运用分析——以反比例函数为例[J].刘志峰.课程教育研究（B）.2017（46）.

[2]初中数学教学中数形结合思想的应用[J].朱家宏.科技视界.2015（09）.

（作者单位：甘肃省永登县武胜驿镇初级中学）