1580热连轧机组轧机主传动系统建模及振动分析①

苏旭涛 计 江 王悦晗 刘 松 宋春阳

(1：中国重型机械研究院股份公司 陕西西安 710032；2：金属挤压与锻造装备技术国家重点实验室 陕西西安 710032；3：常德中联重科液压有限公司 湖南常德 415000)

1 前言

轧机做为一个复杂系统，由多个子系统组成，每个子系统有自身的固有特性。扭振是轧机主传动系统的主要振动形式，也是轧机振动和噪声的重要激励源[1]。

国内某钢厂1580热连轧轧机组由7机架轧机组成精轧段，在进行薄规格产品生产时，F2轧机极易出现异常振动。强烈的振动不仅引起剧烈噪声，严重时振断液压管路，造成严重事故，干扰正常生产[2]。通过建立F2轧机的主传动系统扭振模型，分析其扭振固有特性，通过现场测试信号分析，来分析判断F2轧机的致振原因。

2 主传动系统扭振动力学模型

2.1主传动系统动力学模型的建立

F2轧机的主传动系统的布置情况如图1所示。

图1 F2轧机主传动系统结构简图

根据主传动系统的布置形式，建立动力学模型如图2所示。

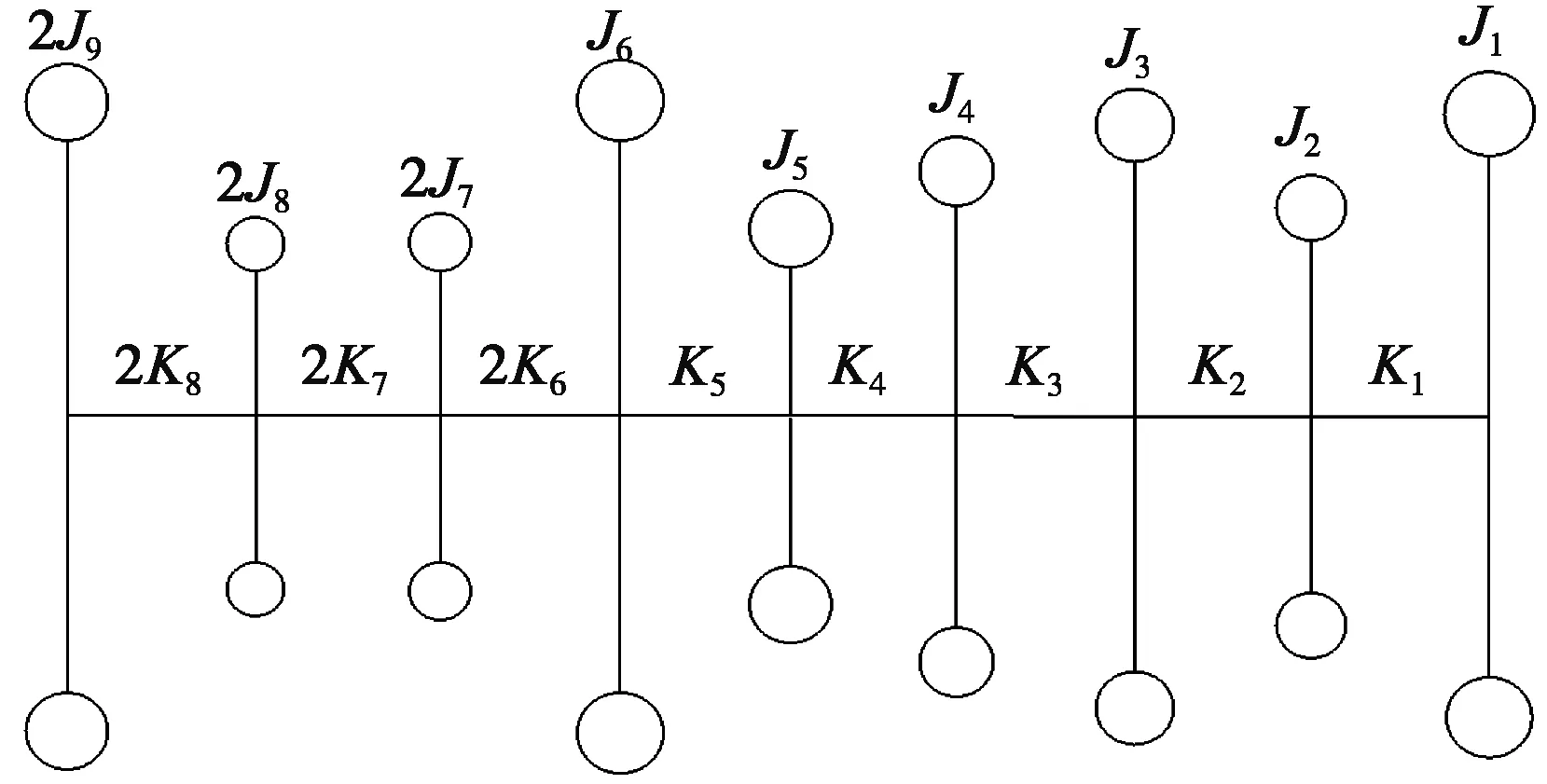
图2 主传动系统扭振动力学模型

2.2 等效转动惯量计算

2.2.1 转动惯量的计算

转动惯量J是刚体绕定轴转动时对其惯性度量的物理量。刚体作定轴旋转时，所有作用在刚体上的外力矩的和等于刚体的转动惯量J与角加速度β的乘积[3]。

(1)

式中ω——刚体角速度(rad/s)；

t——运动时间(s)；

θ——旋转角位移(rad)。

密度均匀的圆柱体绕其中心轴的转动惯量为：

(2)

密度均匀的中空轴的转动惯量为：

(3)

式中ρ——刚体密度(kg/m3)；

l——刚体长度(m)；

D——刚体外径(m)；

d——刚体内径(m)。

形状规则的阶梯轴可简化为几个圆柱轴串联。各圆柱轴转动惯量的和即为阶梯轴的转动惯量。

2.2.2 转动惯量的等效

在主传动系统中，通过减速机和分速机来进行减速和分速，为简化计算，适当调整分支系统的转动惯量。保证系统调整前后动能不变，使主系统与分支系统具有相同转速[4]。

根据上述等效原则，以工作辊转速为基准，计算得到F2轧机主传动动力学模型各集中质量的转动惯量如表1。

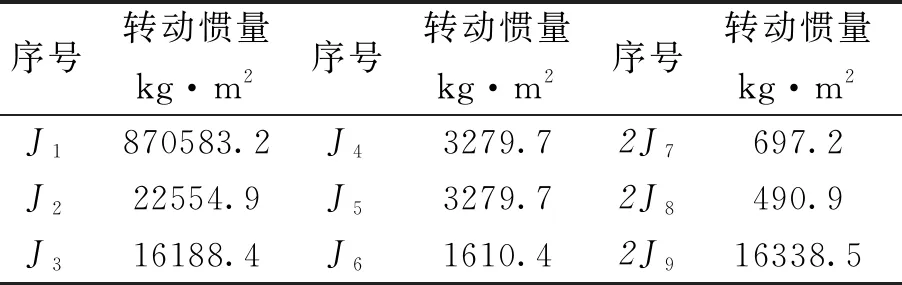
表1 F2轧机主传动系统等效转动惯量

2.3 等效扭转刚度的计算

2.3.1 扭转刚度的计算

使轴段两端产生单位角位移所需的扭转力矩定义为轴段的扭转刚度K。轴段相对角位移Δφ为：

(4)

式中G——剪切模量(N/m2)；

Ip——截面极惯性矩(m4)；

M——力矩(N/m)。

由此可得，轴段的刚度系数为：

(5)

并联轴的等效刚度:

(6)

串联轴的等效刚度：

(7)

式中Ki——各轴段刚度(N/rad)。

2.3.2 扭转刚度的等效

主传动系统中有减速箱，使得连接在减速箱前后的部件具有不同转速，为简化计算，调整分支系统的刚度。保证系统调整前后弹性势能不变，使主系统与分支系统具有相同转速[5]。

根据上述等效原则，以工作辊转速为基准，计算得到F2轧机主传动动力学模型各部分的扭转刚度如表2。

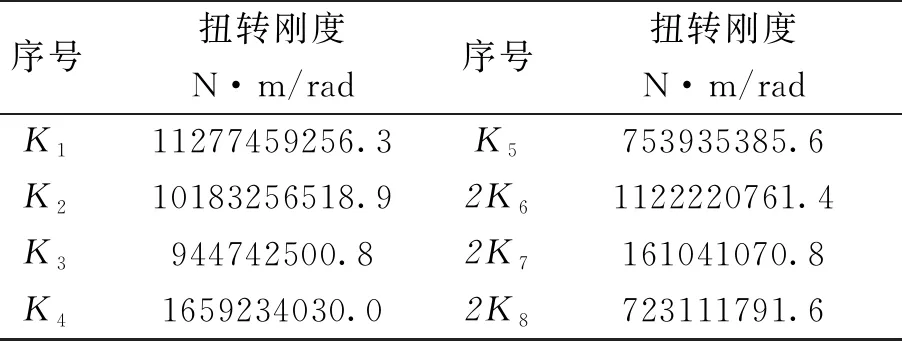
表2 F2轧机等效扭转刚度

3 扭振系统数学模型的建立

3.1 数学模型的建立

采用保守系统的拉格朗日方程，建立主传动系统的数学模型[3]，扭振运动微分方程：

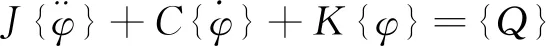
(8)

式中J——转动惯量矩阵；

K——扭转刚度矩阵；

C——阻尼矩阵；

{Q}——激励函数；

{φ}——角位移响应；

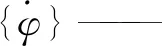
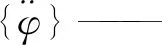
F2主传动系统可简化为一个当量的直串模型。

3.2 系统固有频率和主振型的计算

理想状态下，扭振系统自由扭转振动方程式为

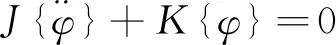
(9)

对方程组(9)求解可得到主传动系统的固有频率和振型。

假设方程组(9)特解(即主振动)为y=Asin(ωt+α)，代入方程得：

(K-ω2J)A=0

(10)

上式有非零解的条件是其系数行列式等于零，即

|K-ω2J|=0

因此，动力矩阵G=J-1K的广义特征值λi和特征向量A(i)(i=1,…,n)就得到系统各阶固有频率和主振型：

φ(i)=A(i),(i=1,…,n)

使用Matlab进行编程计算，程序框图如图3所示。F2轧机主传动系统的各阶固有频率如表3所示。主传动系统前4阶主振型图如图4。

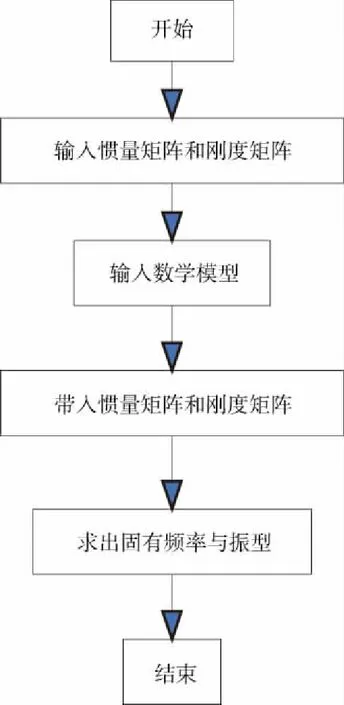
图3 计算程序框图

表3 F2轧机固有频率

4 现场测试信号分析

在现场分别对轧辊的水平振动和轧辊联轴器的扭振进行测试及信号采集，筛选出典型的振动信号进行对比分析。

过图5和图6分析得出，轧辊联轴器的扭振经历了比较明显的四个阶段，第一阶段属于稳定轧制阶段，扭矩信号比较稳定。在第二阶段，上下轧辊联轴器扭振信号振幅明显增大，振动信号接近正弦波，此时振动频率约为18Hz。但现场设备没有出现异常噪声。由于18Hz频率并不是主传动系统的固有频率，排除发生共振的可能。第三阶段，上下轧辊联轴器扭振信号出现扰动，现场出现无规律性的异常噪声。扭振进入第四阶段，现场振动噪声呈现出明显规律性，而且振动稳定，此时振动信号的频率集中在10Hz、40Hz、80Hz附近。对比第二和第三阶段，第四阶段振动信号振幅有所减小且稳定。此时扭振信号频率同主传动系统的第2、第3、第4阶固有频率吻合，可断定在第四阶段主传动系统发生共振。

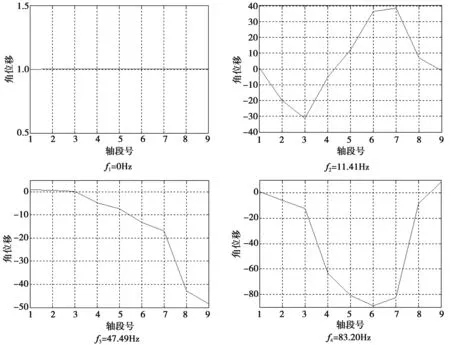
图4 F2轧机各传动部件振型图

图5 上接轴扭振时域图和频域图

图6 下接轴扭振时域图和频域图

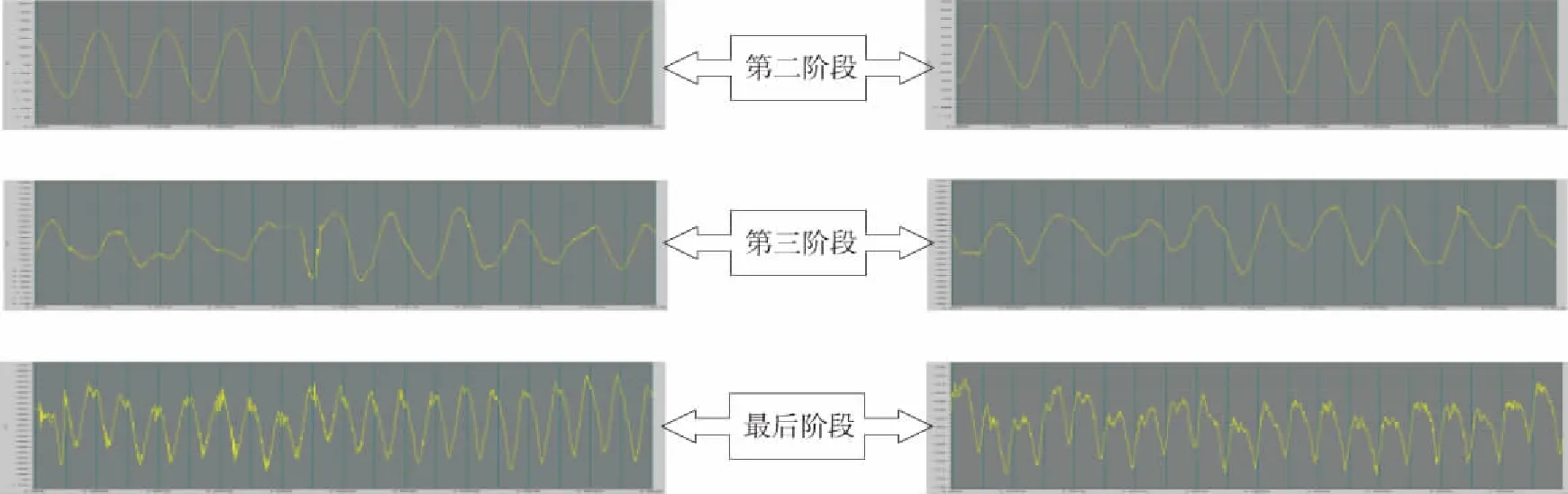
图7 上、下接轴扭振时域图(局部放大)

通过对测试信号进行分析，当联轴器扭矩信号出现明显波动时轧机开始振动。随轧机振动噪声增强，联轴器扭矩信号波动的频率开始加快。扭矩波动经历由低频向高频变化的过程，直至稳定。

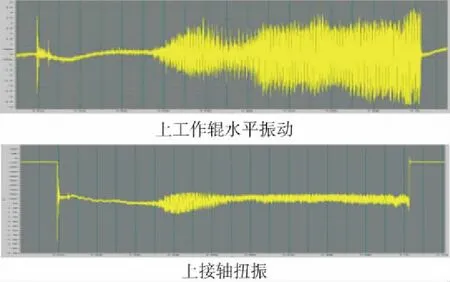
图8 振动信号时域图对比

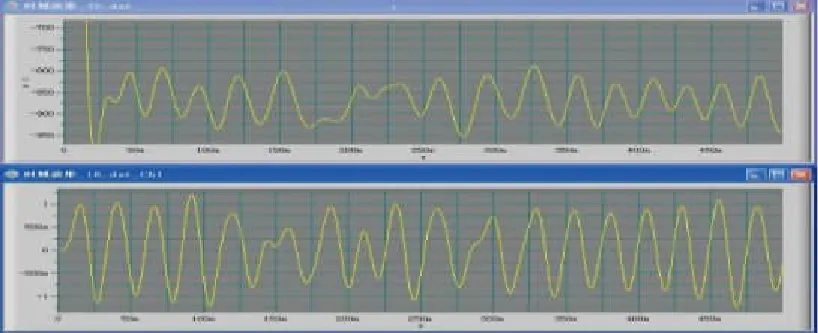
图9 工作辊轴承座水平振动与主轴扭矩波动时域相位对比

将现场收集的轧辊水平振动信号和主传动扭振信号进行对比分析，如图8所示。得出轧辊水平振动和主传动接轴的扭振具有相同的变化规律。二者时域图相位对比如图9所示。对于自激振动，同相位或反相位不会引起振动，90°相位差最易引起振动；对于强迫振动，同相位会引起振动，反相位也会引起振动。因此，可以得出轧辊水平振动和主传动扭振发生了共振。

通过多组信号对比分析，轧辊水平振动信号与联轴器上扭矩信号具有明显一致性，如图8所示。对两者时域信号分析得出，扭振响应滞后水平振动响应0.02～0.04s。两者具有相同的振动集中频率。可以得出，轧辊水平振动是激励源，引发主传动系统扭振。当轧辊水平振动频率和主传动系统固有频率相吻合时会引起主传动系统共振，进而引起整个轧机系统剧烈振动。

5 结论

通过对某钢厂1580热连轧生产线F2机架主传动系统建模，得到主传动系统的动力学模型和数学模型，通过计算得出轧机主传动系统的固有频率和各阶振型。

通过对现场测试信号的分析对比，得出主传动接轴扭振信号可以分为明显的四个阶段，即稳定轧制阶段、受扰振动阶段、共振起振阶段和共振阶段。通过对轧辊水平振动信号和主传动接轴的扭振信号对比分析，得出以下结论，轧辊水平振动信号和主传动接轴的扭振信号具有明显共性，两者振动集中频率保持一致。轧机系统振动的激励源是轧辊的水平振动，轧辊的水平振动导致轧机主传动系统发生共振，进一步引起整个轧机系统的剧烈振动。因此消除或减弱轧辊的水平振动是解决该1580热轧生产线轧机振动问题的根本办法。