例谈习题课之教学功能

边红霞

(河北省易县中学 074200)

习题课一般是根据复习内容就某一知识和方法进行的习题训练，具有示范指导、补充延伸、巩固深化、技能训练、思维提升的功能.最近，连续听高三的习题课，教师大都是讲了一道又一道，缺乏主题呈现、缺乏归纳总结、缺乏深入研究，无效的重复，一节课下来，老师讲得辛苦，学生做题还是一塌糊涂.怎样提高复习课的实效性？由“解题”走向“解决问题”，是数学教学理念上质的飞越.习题课应该成为“解决问题”的主战场，为此，一定要关注训练的目标、训练的功能、训练的方法和训练的价值，从这些方面进行深入剖析，才能发挥习题课的最大功效.

一、训练的目标——注重考纲 示范引领

例1(2018年高考全国课标卷理科第9题)

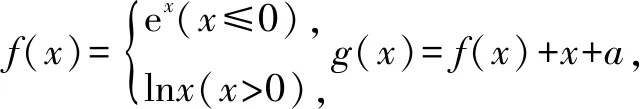
A.[-1,0) B.[0,+∞)

C.[-1,+∞) D.[1,+∞)

分析f(x)是分段函数，函数g(x)=f(x)+x+a存在两个零点，转化为方程f(x)+x+a=0有两个根，转化为f(x)=-x-a有两个零点，构造函数h(x)=-x-a，转化为f(x)与h(x)=-x-a的图象有两个交点.利用数形结合，由图象可知，函数h(x)=-x-a的截距需满足-a≤1，即a≥-1，故选项为C.

运用有意注意认知规律，在组织教学中要进行学习目标教育，明确学习目标是什么？每一部分内容具体要求是什么？目的越明确，注意就越容易集中，有利于学生充分理解和掌握知识方法.

1.关注考纲要求

考纲是数学复习的行动纲领，是复习内容的出发点和落脚点.在习题课上决不仅仅是解题，而要关注解决怎样的问题？怎样解决问题？解决到什么程度？从而以点带面，起到示范引领的作用.因此，在讲解习题之前，首先要对考纲进行研究，要明确涉及的内容在大纲中的具体要求,达到的深度与广度,从而规划解题方案.

此题完美地诠释了大纲对函数的要求.尽管是一道选择题，但也尽显其考查功能，它既考查了分段函数的概念，运用了化归、分类讨论、函数与方程、数形结合等思想.尤其是函数与方程思想运用得淋漓尽致，是一道典型的函数问题.

2.示范引领作用

解决此类问题时，其示范性方法及思路是：将函数零点转化为方程的根，进而再构造函数，转化为图象交点问题，最后用数形结合思想解决，体现了函数零点的两种形态：从“数”的角度看，是使f(x)=0的实数x；从“形”的角度看，是函数f(x)的图象与x轴交点的横坐标.

解完题后，教师不能立刻收笔，要就此大做一番文章，对它所拥有的解题思路和方法进行归纳总结，寻找和发现解题规律，给学生示范与启发，从而指导学生思考和解决新的问题，达到以不变应万变之功效.习题课把静态的知识变得鲜活起来，让学生在这种灵动的课堂上，实践解决问题的一般方法，发现解决问题的一般规律，体验问题解决的喜悦与成功！

二、训练的功能——通性通法 技能训练

例2(2019年1月保定市模拟考试第22题)已知函数f(x)=x3+(k-1)x2+(k+5)x+d，

(1)若k=1，求函数f(x)的单调区间；

(2)若f(x)在区间(0,3)上不单调，求实数k的取值范围.

解析(1)略.

(2)f′(x)=3x2+2(k-1)x+k+5.因为f(x)在区间(0,3)上不单调,问题转化为f′(x)=0在(0,3)上有实数解，且无重根.

1.提炼通性通法

通性通法，是指具有某些规律性和普遍意义的常规解题模式和常用的数学思想方法，习题课中要选用典型的习题，通过分析，展示解决问题的通性和通法，从而训练学生的数学技能.近几年，高考数学试题坚持淡化技巧、注重对通性通法的考查.函数与方程是两个相辅相成的概念，是一衣带水的关系，彼此之间感情深厚，因此经常互相帮扶，总是在关键时刻伸出援助之手，这是解决函数零点问题的通性和通法.

2.关注技能训练

数学技能是顺利完成某种数学任务的动作或心智活动方式.它通常表现为完成某一数学任务时所必需的一系列动作的协调和活动方式的自动化.这种协调的动作和自动化的活动方式，是在已有数学知识经验基础上，经过习题课上的反复训练而形成的.因此，习题课要具有一定的主题呈现，围绕此主题精选习题，并在解题的过程中，反复呈现解决此类问题的常用手法，通过集中训练而形成解决问题的技能.

三、训练的方法——自主感悟 合作探究

例3 已知f(x)=2ax-x3(a>0),在下述条件下分别求参数a的取值范围.

(1)在(0,1)上单调增；

(2)在(2,3)上存在单调区间；

(3)f(x)单调区间是(-1,1).

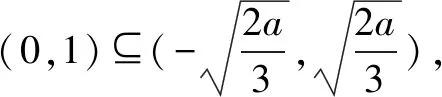
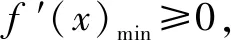
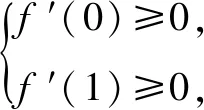
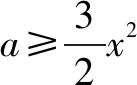
同学7：(2a-3x2)max≥0，解得a≥6，检验当a=6时，f′(x)=-3x2+12，不成立，综上a>6.

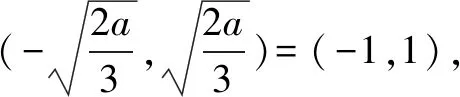
1.自主感悟

让学生主动学习、自主发展是新课标中教学目标的核心内容.学会合作是一种重要的能力，教师的角色是成为学生学习的促进者，在教师的带领下，让学生在自主探究中，尝试面对困难的勇气，体会数学的乐趣，收获数学的价值！因此在习题课中，教师要努力营造更加民主的氛围，鼓励学生去思考、去探讨、去合作，必要时再给以支持和指导.

2.提倡合作探究

打造高效的学习效率，需要师生、生生形成密切的合作关系，它是一种教学形态 ，集中表现为教师教得轻松，学生学得愉快，这是教师追求的教学理想，也是课堂教学的动力和目标.高效教学要求教师不断地学习、反思，提高自身素质和科学技能，尤其是对发展深化的数学，更要求教师持续的开阔知识视野，提高自己的教学水平，这样才能自如地驾驭课堂，在课堂上教师能够潇洒的放出去，让学生充分讨论，又能适时果断地收回来，达成共识的解决方案，就像风筝一样，我们要放飞它，让它在数学的天空中自由自在的飞翔，同时，我们还要给它方向和目标的指引，这样才能让学生在感悟中得到思维的提升.

四、训练的价值——提升思维 素养导向

(1)讨论f(x)的单调性；

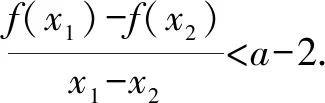
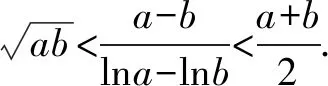
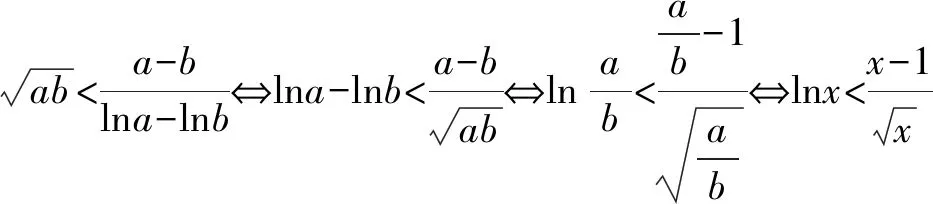
构造函数：

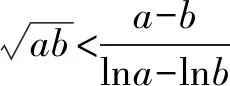
当且仅当a>2时，f(x)存在两个极值点x1,x2,满足方程x2-ax+1=0,x1x2=1,

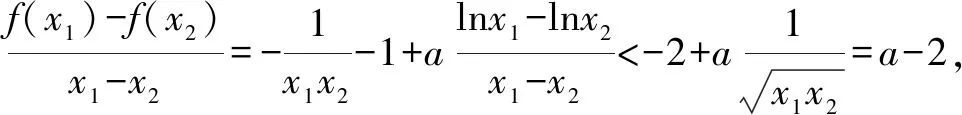
1.注重思维的提升

新课标特别关注数学核心素养的形成和发展，提出了两个转变，一个转变是关注学生核心素养的达成；一个转变是考查学生的思维能力.教育部考试中心任子朝先生在他的一篇文章中提出“中国高考正在实现从能力立意到素养导向的历史性转变”.“数学教学是数学思维的教学”，注重思维培养与提升是数学教学的核心.因此在习题课的教学中，教师的教学一定要尊重学生学习的主体地位，激发学生的主观能动性，培养学生良好的学习习惯.并在习题课中做到解一题，带一串，通一类，提升学生的思维，提高学生解题效率和解题能力，最终实现培养学生的核心素养.

2.关注核心素养

本题充分考查了学生的数学运算、数学抽象、数学建模、逻辑推理等数学素养，考查了学生灵活应变能力、发现问题、解决问题的能力，要求学生具备扎实的数学素养和宽广的数学视野. 近几年高考试题依据考试大纲，鼓励“课内功夫”，强调知识内化，助益融会贯通；加强灵活性考查，促进真懂会用，突出了两个转变，体现了高考试题的积极导向，对此目标的达成，习题课起着不可替代的桥梁作用.

习题课使学生在能力上全方位锻炼，知识上横向与纵向关联，是学生思维提升的最佳平台，也是提高学生数学素养的有效途径.为适应迅猛发展的新形势，素养导向的高考复习，已经把学生的解题转变为解决问题，最终将做题转变为做人、做事.在习题课的教学中，教师要转变观念，赋予习题课一定的话语权，使它成为学生能力素养提高的一场盛宴.